The Distances to Nearby Stars
Additional reading from www.astronomynotes.com
Historically, the stars in the sky were considered to be simply a background of lights affixed to the celestial sphere. All stars appear to the naked eye as points of light, and their positions relative to each other never seem to change. However, the positions of nearby stars actually do move by tiny amounts, and if we can measure this apparent motion, we can calculate the distance to these stars using some simple trigonometry. This idea was actually well known to the Greeks and was an idea that was used to argue against the heliocentric model for the Solar System. As you will see momentarily, the argument goes that if the Earth orbits the Sun, then we should be able to see the nearest stars shift on the sky. Since this shift was not observed by the Greeks, nor by later astronomers like Brahe, they argued for a stationary Earth as the center of the Solar System. What they did not count on is the immense distance to the stars, which made the shift so small it was not able to be detected until the 1830s. The first scientist to do so was Friedrich Bessel in 1838.
The method that is used to measure distances to nearby stars is called trigonometric parallax, or sometimes, triangulation. This is actually the same technique that your brain uses to judge distances to the objects around you—your so-called “depth perception.” You can demonstrate this technique for judging distances with a simple experiment:
- Hold your arm out in front of you at eye level, and raise your index finger.
- Close your left eye, and note where your finger appears to be with respect to the background (the wall of the room you're in, for example).
- Open your left eye and close your right eye, and now note where your finger appears to be with respect to the background. It appears to have moved! (you can see this effect easily if you quickly alternate which eye is closed—first left, then right, then left, then right).
- Bend your elbow so that your finger is now much closer to your eye than when you held your arm out straight.
- Repeat the process of observing your finger with one eye opened and one eye closed. When your finger is much closer to your eyes, the apparent movement with respect to the background is much larger!
Because your eyes are separated by a few inches, your left eye sees a slightly different view of an object than your right eye. When your brain interprets the two images from your eyes, it allows you to estimate the distance to objects.
Of course, stars are so far away that the separation between our eyes does not make any difference in their appearance. However, we can use Earth’s orbit as a baseline to create separate images of nearby stars. In January, the Earth is on one side of the Sun (consider this the “left eye” position), and 6 months later, in July, the Earth is on the other side of the Sun (the “right eye” position). The distance between the Earth’s position in January and its position in July is twice the Earth/Sun distance, or 2 AU. When you observe a nearby star in January, and then again in July, its position with respect to much more distant, background stars will have changed by a measurable amount, as illustrated in this animation.
Using trigonometry, we can calculate the lengths of the sides of a right triangle with some simple equations. We can setup a right triangle if we use half of the measured angle that the star appears to move in 6 months. The distance to the star (d), the angle by which the star appears to have moved (θ), and the length of the baseline (b) are related in the following way:
We call the angle the "parallax," or just p, of the star (some folks use , like the creator of the diagram below, but I'll use just p). The length of the baseline is 1 AU, since we are using half of the angle. The reason we use half of the angle and half of the baseline to form a right triangle for the calculation is illustrated in the diagram below:
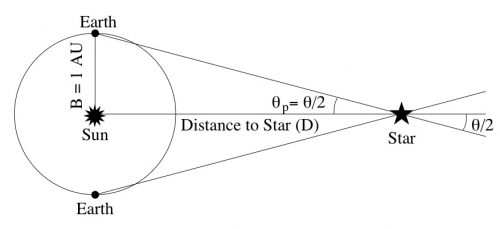
I want to emphasize that the parallax angles that we measure are incredibly tiny. If you were to create a right triangle using the diameter of a U.S. dime as one side and a distance of 2.4 km as the other side, the small angle in this triangle is about 1.5 arcseconds (remember, an arcsecond is 1/3600th of a degree). The nearest star to Earth, Proxima Centauri, undergoes a shift of 1.5 arcseconds in apparent position every 6 months. So every other star in the sky has an angular shift smaller than the diameter of a dime seen at a distance of 2.4 km!
The unit of measurement for distance that astronomers use is called the parsec (pc). This comes directly from the measurement of parallax for stars, because 1 parsec is the distance to a star with a parallax angle of 1 arcsecond. Parsec is an abbreviation for parallax arcsecond. Another unit that astronomers use for distance is the light-year, which is the distance a photon of light travels in 1 year. These two measurements are similar, and:
To calculate the parallax of any star, you can use the same trigonometric relationship that we discussed in lesson 3 when we talked about the headlights of a car. In this case:
B = the baseline of 1 AU, so:
Since D is the quantity that we would like to measure, we can rearrange this equation to read:
If you enter your angle for p, your answer for D will come out in AU. If you enter 1 arcsecond for your angle, D will come out to be 206,264.8 AU, the definition of a parsec given above.
You can simplify this equation, though. For sufficiently small angles expressed in radians (and 1 arcsecond is a sufficiently small angle):
, so:
as long as your value for p is a small angle.
to convert from arcseconds to radians, you would use:
or,
If we substitute this into the equation above you get:
, or
but since you have:
since the quantity appears on the top and bottom of the equation, you can cancel it out, and you are left with:
So, for any parallax angle given in arcseconds, the distance to that star in parsecs (abbreviated pc) is simply .
For example, if you have a star with a parallax of 0.5 arcseconds:
Parallax measurements have traditionally been made with photographs taken by refractors at ground-based observatories, such as the United States Naval Observatory, the University of Virginia Leander McCormick Observatory, the Allegheny Observatory of the University of Pittsburgh, Sproul Observatory of Swarthmore College, and the Yale University observatory. However, in recent years the Hipparcos satellite mission has provided parallax measurements for more than 100,000 stars out to distances of approximately 100 parsecs, and the European Space Agency Gaia mission will improve upon those measurements in years to come. Although this topic is always described in exactly this way (that is, you measure the star's position in two precise locations on dates exactly 6 months apart), in practice, you can observe a star continuously and measure its subtle shift over the entire course of that six month time period. The images used to measure stellar parallax look nothing like the images you are used to seeing of the sky. Here is an image of a glass photographic plate from the UVa collection of a star in their parallax program:

On this plate, you can see rows of dark grey dots -- those are stars. In order to save plates (which were a pretty precious commodity), a single star would be observed, then the plate would be shifted, exposed again, shifted, exposed again, shifted, etc., sometimes putting 5 or 6 exposures of the sky on one plate. Then, to get additional use out of the plate, it would be turned 180 degrees and exposed 5 - 6 more times in the reverse orientation. The red marks show the location of stars of interest on the plate exposed in one orientation, and the blue marks mark the location of the same stars in the reverse orientation. This plate would then be measured with a machine able to centroid a star's location to an accuracy of a fraction of a micron. Measuring these plates was one of this course's author's summer jobs as an astronomy student, and if you visit in person, they do exhibit some of the measuring machines used for this work.