The Rotation Curve of the Milky Way
Additional reading from www.astronomynotes.com
Now that we have a concept of the size, stellar populations, and an overall understanding of the Milky Way as a galaxy, let us consider another property that we can determine for the Milky Way: its mass. In most instances, when we intend to calculate the mass of an astronomical object, we return to Newton's version of Kepler's third law:
The Sun is orbiting around the Galactic center, so in principle, if we can measure the Sun's distance from the Galactic Center and its orbital period, this means we can estimate the sum of the masses of the Sun and the Galaxy (at least the portion of the Galaxy that is interior to the Sun's orbit). Since we anticipate the Galaxy's mass to far exceed the Sun's mass, we can take the value that we calculate to be the Galaxy's mass. So, what is the answer? How massive is our galaxy?
The distance from the Sun to the Galactic Center can be measured using a few different techniques, but it is a difficult measurement to make. It is still the case that researchers disagree about the exact value, but it is approximately 8 kpc (that is, 8,000 parsecs). There is a related, but also difficult measurement to make, and that is the velocity of the Sun with respect to the Galactic Center. It is approximately 200 km/sec, which allows us to estimate the period of the Sun's orbit around the Galactic Center in the following way:
- Assume the Sun is following a circular orbit with radius 8,000 parsecs.
- Calculate the circumference of the Sun's orbit: .
- Calculate the period of the orbit by taking the circumference and dividing by the velocity: .
If you take the semi-major axis of the Sun's orbit to be 8 kiloparsecs and the orbital period to be 250 million years, you can determine that the Milky Way's mass interior to the Sun's orbit is approximately 1011 solar masses, or 100 billion times the mass of the Sun.
Now, let us compare and contrast motions in the Solar System of the planets and motions in the Galaxy of the stars. What we did above to calculate the period of the Sun's orbit was to use the equation:
We can rearrange this equation and calculate orbital velocity for any object given its period and semi-major axis. If we apply this to the planets in the Solar System, you find that as you get more distant from the Sun, the orbital velocity of the object is slower. Below is a two-dimensional plot that I created for the orbital velocities of the planets (and Pluto) as a function of their distance from the Sun. Each point is labeled with the first letter of the object's name (e.g., V = Venus). This type of plot (orbital velocity as a function of distance from the center) is referred to as a rotation curve.
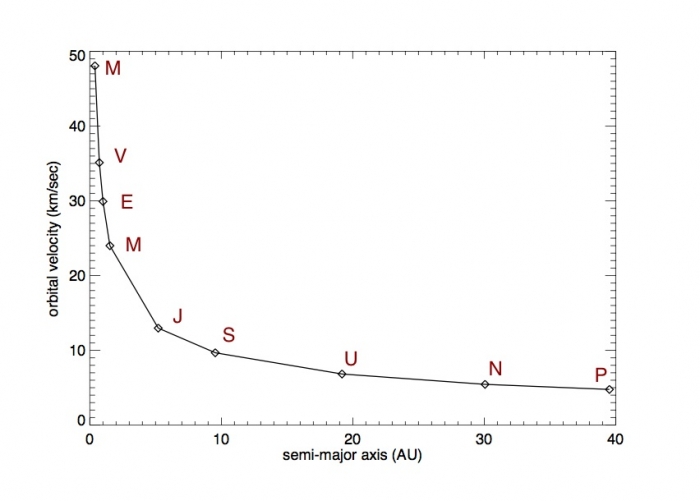
The behavior of the planets in the Solar System as exhibited in this plot is often referred to as Keplerian Rotation. Clearly, the Milky Way Galaxy is more complicated than the Solar System. There are at least 100 billion objects, gas clouds, and dust, and there is not one single dominant mass in the center. However, astronomers expected that as you got more distant from the center of the Galaxy, the velocities of the stars should fall off in a manner similar to the Keplerian rotation exhibited by the planets in the Solar System. However, astronomers have observed that there is a significant difference between the predicted shape of the Milky Way's rotation curve and what is actually measured. See the image below.
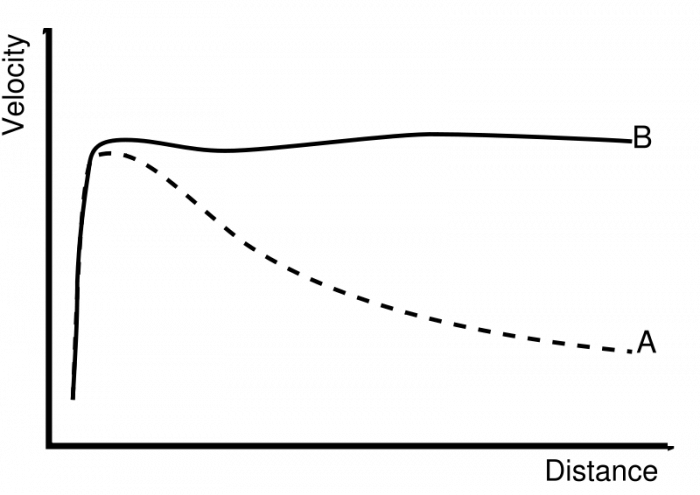
The solid line labeled B is a schematic rotation curve similar to what is measured for the Milky Way. The dashed line labeled A is the predicted rotation curve displaying Keplerian rotation. What the rotation curve B tells us is that our model of the Milky Way so far is missing something. In order for objects far from the center of the Galaxy to be moving faster than predicted, there must be significant additional mass far from the Galactic Center exerting gravitational pulls on those stars. This means that the Milky Way must include a component that is very massive and much larger than the visible disk of the Galaxy. We do not see any component in visible light or any other part of the electromagnetic spectrum, so this massive halo must be dark. Today, we refer to this as the "dark matter halo" of the Galaxy, and we will discuss dark matter more in our lesson on cosmology.
Returning to the image of the Milky Way that we studied before, the wire frame halo is actually meant to represent the extent of the dark matter halo. In the image below, compare the scale of the disk to the scale of the dark matter halo.