Additional reading from www.astronomynotes.com
- The Sun's Power Source
- Stellar Evolution: Stage 6 Core Fusion
- Stellar Nucleosynthesis
- Neutrino

By the time clumps inside of a GMC have become T Tauri “stars,” they are still not truly stars. The event that triggers the change of an object into a star is the onset of nuclear fusion in the core.
Much of the gas inside all protostars is hydrogen. Recall a few things about hydrogen from previous discussions:
- Hydrogen is the simplest atom with a single electron and a nucleus of a single proton.
- If the electrons in a gas of hydrogen atoms absorb enough energy, the electron can be removed from the atom, creating hydrogen ions (that is, free protons) and free electrons.
By the time a collapsing gas cloud has become a protostar, its core has reached a temperature of several million kelvin. At this temperature, the hydrogen in the core will be a plasma, a "soup" of hydrogen ions and electrons moving around at very high speed. Particles of like charge repel each other, so if you take two protons (both have the same positive charge) and try to push them together, the electrical force between them will provide resistance. Inside of a protostellar core, the temperature and density are high, so the protons are packed together very tightly and are moving very rapidly. When the temperature reaches a high enough point (about 10 million kelvin), the protons are moving so fast inside the core that the electrical repulsion cannot prevent them from colliding. Once they collide, they fuse together in a process that generates energy.
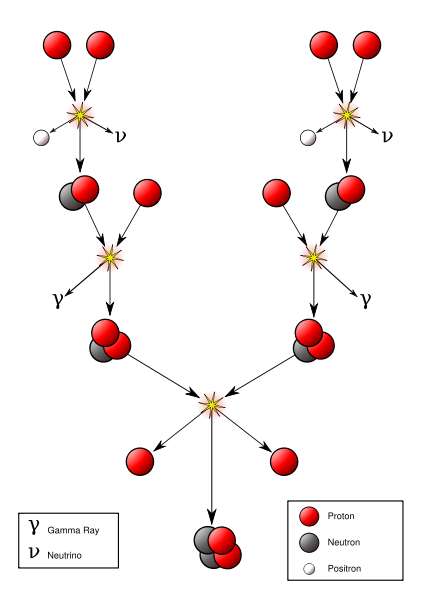
Inside the core of a star like the Sun, fusion proceeds via a process called the proton-proton chain. In this multi-step process, six protons fuse together and the product is a helium nucleus and two protons.
Here are the steps in equation form:
Here are the steps laid out in flow chart form:
Here are the players:
- can be referred to as hydrogen ions, hydrogen nuclei, or free protons.
- are deuterium ions or nuclei.
- are 3-helium ions or nuclei.
- are helium ions or nuclei or "alpha-particles".
- Positrons are the anti-particle equivalents of electrons, and when they encounter electrons they annihilate, creating a gamma ray photon.
The steps in the proton-proton chain are all happening at once in the core of a star, but, at a minimum, you need step one to happen twice to create two deuterium nuclei, step two to happen twice to create two 3-helium nuclei, and the result of step three is a single helium nucleus and two hydrogen nuclei. This means that the input to the process requires six hydrogen nuclei to fuse, but you get two of them back at the end, so, overall, you can summarize the proton-proton chain in this way:
This process uses up hydrogen but creates new helium, because after the reactions have finished, you have four fewer protons than you started with, but one more helium nucleus. The mass of one helium nucleus is smaller than the combined mass of four protons, so, in this process, mass has been lost. The mass that gets lost in this process has actually been converted into energy. Einstein's famous equation:
tells us that the energy (E) generated equals the mass lost (m) times the speed of light squared ( ). The speed of light squared is a big number, so even though the amount of mass lost in this process is small, the amount of energy generated is large. Since stars contain a massive amount of hydrogen, large quantities of protons are fusing in their cores every second. For example, if you calculate how much hydrogen must be converted to helium each second in order to generate the measured luminosity of the Sun, you find that approximately half of a billion tons of hydrogen is being converted into helium each second. At that rate, the Sun has enough hydrogen in its core to continue generating energy via the proton-proton chain for another 5 billion years.
The mass difference between the helium nucleus and the hydrogen nuclei is . So, the energy released is:
each time the proton-proton chain creates one helium nucleus. You can use this information to estimate the lifetime of the Sun or any other star in the following simple way:
- Calculate how much hydrogen is available to power fusion in the star's core.
- Calculate how much total energy the star can generate if it converts all of its core hydrogen into helium at the rate of per reaction.
- Calculate the lifetime of the star as the total energy it can generate by hydrogen fusion divided by the rate at which it is emitting that energy (i.e., its luminosity).
This ignores several important details, but for a typical Sun-like star, you determine that it can shine by hydrogen fusion for approximately 10 billion years.
So, now that we know how energy is generated inside a star via nuclear fusion, we can answer the following question: Why does the onset of nuclear fusion signal the transition of a protostar into a true star? The answer is that the nuclear fusion generates energy, and this energy provides enough radiation pressure to finally balance the inward pull of gravity, stopping the contraction that began when the clump of gas began to collapse in on itself. The energy generated in the star is being radiated outwards as photons of light. As the photons pass through the star, they created a net outward push (radiation pressure), which along with the thermal pressure of the material in the star, resists gravity. When the force of gravity is exactly balanced by the total pressure, we say that the star is in hydrostatic equilibrium.
There are several final points that should be mentioned on this page. The temperature that the core of a protostar reaches depends on its mass. The more massive the protostar, the hotter it gets. If the core reaches a high enough temperature (more than 20 million kelvin), a different set of fusion reactions proceed more efficiently than the proton-proton chain. This process, called the CNO (carbon-nitrogen-oxygen) cycle, occurs in stars more massive than the Sun. The CNO cycle still requires hydrogen to proceed, so even in these stars the main fuel for the fusion reaction is hydrogen. In both the proton-proton chain and the CNO cycle, one element is being converted into another via nuclear fusion. This process of creating new elements is called nucleosynthesis.
Finally, if there is no way for us to directly observe the core of a star, how do we know that nuclear fusion is indeed its power source? The answer is in the first step of the proton-proton chain—the process also generates neutrinos. Neutrinos can pass through large quantities of matter (e.g., the entire Sun) without interacting in any way, so the neutrinos that are generated leave the Sun and travel through space. They are very difficult to detect, but on Earth, several experiments have detected solar neutrinos, verifying the Sun's core is generating energy via the proton-proton chain. In 2002, the Nobel Prize in physics was awarded to Raymond Davis for the detection of neutrinos from the Sun.
Want to learn more?
Check out Raymond Davis's biography, complete with photos of his experiments!