Lesson 2
Overview
About Lesson 2
Like many students, you may have come into a course on astronomy thinking that we would spend an entire semester on night sky observations. What we really want to study, though, is astrophysics—we want to understand how those objects that you can observe behave and why they behave the way they do. Traditionally, this is taught from a historical perspective. We will see how over long periods of time we went from making observations of the objects in the sky to the first understanding of those objects.
In this lesson, we are going to begin studying the fundamental physics that is the foundation of astronomy; for now, we will focus on the orbits of the planets around the Sun and the force of gravity. The story involves many of the most famous scientists from throughout history: Aristotle, Ptolemy, Galileo, Copernicus, Newton, and some famous astronomers that you may not be as familiar with—Tycho Brahe and Johannes Kepler. The story of how our understanding of the solar system and the Earth’s place in it evolved is an excellent example of the process of science and how accurate observations can force us to change some of our most fundamental theories about the universe.
What will we learn in Lesson 2?
By the end of Lesson 2, you should be able to:
- interpret the observational evidence for a heliocentric Solar System;
- quantitatively compare and contrast the shape of the planetary orbits and the relationships between their distances from the Sun and their orbital periods;
- explain how an orbit is a balance between the force of gravity and the tangential motion of an object;
- describe how the orbital properties of an object can be used to determine the mass of the system.
What is due for Lesson 2?
Lesson 2 will take us one week to complete. Please refer to the Calendar in Canvas for specific time frames and due dates.
There are a number of required activities in this lesson. The following table provides an overview of those activities that must be submitted for Lesson 2.
| Requirement | Submitting Your Work |
|---|---|
| Lesson 2 Quiz | Your score on this Canvas quiz will count towards your overall quiz average. |
| Lesson 2 Practice Math Problems | There is a second quiz for this lesson in the Lesson 2 Module in Canvas. This one is all short math problems. You will be graded only on effort on this quiz, that is you will be graded for taking it and working on the problems, but not on your answers. |
| Lab 1 | During Lesson 2, you should begin taking data for the "Moons of Jupiter" lab you will complete at the end of Lesson 3. You do not need to submit anything this week. |
Questions?
If you have any questions, please post them to the General Questions and Discussion forum (not email). I will check that discussion forum daily to respond. While you are there, feel free to post your own responses if you, too, are able to help out a classmate.
Naked Eye Observations
Additional reading from www.astronomynotes.com [1]
Prior to the invention of the telescope, an observer could see the following objects with the unaided eye:
- The Sun;
- The Moon;
- The five planets: Mercury, Venus, Mars, Jupiter, and Saturn;
- The stars.
If you recall from Lesson 1, we discussed that the position of the Sun in the sky appears to drift with respect to the background stars (we didn’t discuss it in depth, but the Moon also drifts with respect to the stars–this should be more obvious because we can observe it night after night!). We can’t see the stars during the day, so the Sun’s drift is not obvious to most of us. However, we know that many civilizations in the pre-telescopic era were familiar with the drift of the Sun with respect to the stars. For example, they carefully studied the heliacal risings and settings of stars and used these to mark dates on their calendars. The heliacal rising of a star is the first day it is visible just before dawn, which is a direct indication of the Sun’s drift with respect to the stars. If the Sun happens to be from our point of view in front of a particular star, say Sirius, that star will rise just before dawn only on one day of the year. The next day, Sirius will rise four minutes earlier because of the Sun’s eastward drift along the ecliptic.
Check this out...
There is more information on helical risings from Stanford on their site: "Ancient Observatories, Timeless Knowledge [3]".
As you can see from the list in the first paragraph, there are only five planets visible to the naked eye. For these same observers, what distinguished planets from stars is, again, their motion. Planets also appear to drift compared to the background stars but in a more complicated manner than the Sun.
Test this with Starry Night!
Let's investigate two examples...
- Open up Starry Night. Set it to the following:
- location = somewhere in Pennsylvania
- date & time = May 6, 2008 @ 9:30pm
- time flow rate = 1 sidereal day
- constellation labels and stick figures turned on (if you press "k" on the keyboard, it accomplishes this for you without having to use the menu or options tab)
- Press play (or click on the forward one step button at least a dozen times), and you will watch Mars' location change with respect to the stars over the course of a few weeks or a few months.
- For the second example, open a new Starry Night session and set it to the following:
- date & time = June 6, 2003 @ 3:30am
- Otherwise, use all of the same settings as you used above.
- Again, press play or click on the forward one step button at least a dozen times. How did the path of Mars differ between the two examples?
Below is a composite image created of Mars during the 2003 time period you simulated with Starry Night:

You may want to try to avoid reading the caption at this link, though, because it gives away the punchline to this lesson.
If you study your Starry Night path of Mars or the APOD image above, you will find that the first part of Mars’ motion is prograde, or eastward compared to the stars, just like the Sun. However, around July 30, Mars has slowed down and proceeds to move retrograde, or westward compared to the stars. Then, it slows down again and begins prograde motion again! If you study the other naked-eye planets, for example, Jupiter and Saturn [7], you find that they exhibit the same behavior. This path is often referred to as a "retrograde loop." Again using Mars as an example, its retrograde loop is not always identical. The dates of the beginning and ending of the retrograde loop, the shape of the path of the loop with respect to the stars, and the point along the ecliptic at which the loop begins changes.
For the rest of this lesson, we are going to again study the geometry and motion of the solar system and, by the end, we will show that we can easily explain this complicated motion of Mars. While this seems simple in retrospect, it took thousands of years for scientists to determine the solution!
The Geocentric Model
Additional reading at www.astronomynotes.com [8]
Scientific Models
Before returning to retrograde Mars and beginning our discussion of the early attempts to explain this behavior, let's first discuss scientific models. This is terminology that is now being included in state science education standards and the Next Generation Science Standards (NGSS), and I want to be quite clear about what I mean when I use the term in this class.
To astronomers and other scientists, “making a model” has a specific meaning: taking into account our knowledge of the laws of science, we construct a mental picture of how something works. We then use this mental model to predict the behavior of the system in the future. If our observations of the real thing and our predictions from our model match, then we have some evidence that our model is a good one. If our observations of the real thing contradict the predictions of our model, then it teaches us that we need to revise our picture to better explain our observations. In many cases, the model is simply an idea—that is, there is no physical representation of it. So, if, when I use the word "model," you picture in your head a 1:200 scale copy of a battleship that you put together as a kid, that is not what is meant here. However, that doesn't preclude us from making a physical representation of the model. So, for example, if you are studying tornadoes, you can build a simulated tornado tube using 2 liter soda bottles filled with water. However, for it to be useful as a scientific model, you would want to use the physical model to try and study aspects of real tornadoes. In modern science, many models are computational in nature—that is, you can write a program that simulates the behavior of a real object or phenomenon, and if the predictions of your computer model match your observations of the real thing, it is a good computer model.
This is also a good time to introduce a statement referred to as Occam’s Razor. This is a simple statement that paraphrased says: If there are two competing models to explain a phenomenon, the simplest is the one most likely to be correct. This concept was taught to me in the following way: if you propose a model, you are only allowed to invoke the Easter Bunny once, but if you have to invoke the Easter Bunny twice (as in “then the Easter Bunny appears and makes this happen"), your model is probably wrong.
Want to learn more?
For more history, see a discussion of Occam's Razor on Wikipedia [12]. I realize that Wikipedia is not always to be considered a trusted resource, but this is a good overview.
What I hope will be made clear in the rest of the course is that in practice science is very non-linear. In fact, as a fairly frequent judge for the "Pennsylvania Junior Academy of Science" (which may be similar to science fairs where you teach), I often complain about their rubric for judging, because they force students to try to approach science in a linear, step-by-step model. Scientists all do the standard steps of the scientific method at some point, however, not necessarily in the order presented in textbooks or in a way that they identify as "Now I am on step 5 of the process", for example. This process is really completed by a community of scientists working on scientific problems separately. Everyone involved in the process is working towards the same goal, but some may contribute observations while others build better models, for example. If you would like to discuss this more, this would be an excellent topic for Piazza!
The Greek's Geocentric model
Traditionally in Astronomy textbooks, the chapter on the topic of the motion of the planets in the sky almost always begins with mention of the ancient Greeks. I will not go into a lot of detail on the lives and accomplishments of Eratosthenes, Aristarchus, Hipparchus, etc., but I will follow tradition, and we will study here the model of the Universe presented by the Greeks. In particular, we will consider the work of Aristotle and Ptolemy, because their model was considered the best explanation for the workings of the solar system for more than 1000 years!
While I will gloss over most of the discoveries of the famous Greek philosophers (or mathematicians or astronomers, whatever you prefer to consider them), I think it is quite important to note that they were able to determine many sophisticated understandings of our Solar System based on their strong grasp of geometry. For example, Eratosthenes is given credit for demonstrating that the Earth is round and for performing the first experiment that resulted in a measurement of the circumference of the Earth [13].
Try This!
If you aren't familiar with Eratosthenes' experiment, I encourage you to spend time at the website above and to even consider repeating the experiment if you can find a partner located several hundred miles from your school.
Now, let's return to a discussion of the Greeks' model. Today, we start with our well known laws of physics as the basis of our scientific models. At the time that the Greek model was being developed, those laws were unknown, though, and instead they held firmly to several beliefs that formed the foundation of their model of the solar system. These are:
- the Earth is the center of the universe and it is stationary;
- the planets, the Sun, and the stars revolve around the Earth;
- the circle and the sphere are “perfect” shapes, so all motions in the sky should follow circular paths, which can be attributed to objects being attached to spherical shells;
- objects obeyed the rules of “natural motion,” which for the planets and the stars meant they orbited around the Earth at a uniform speed.
Given this set of rules (in modern scientific language, these would be referred to as the assumptions of the model; however, the Greeks believed these to be laws that could not be altered), the Greeks constructed a model to predict the positions of the planets. They knew about retrograde motions, and, therefore, they also constructed their model in such a way to account for the retrograde motions of the planets. Their model is referred to as the geocentric model because of the Earth’s place at the center.
Our knowledge of the Greek’s Geocentric model comes mostly from the Almagest, which is a book written by Claudius Ptolemy about 500 years after Aristotle’s lifetime. In the Almagest, Ptolemy included tables with the positions of the planets as predicted by his model. If you recall from our previous discussion, the retrograde motions of the planets are very complex; therefore, Ptolemy had to create an equally complex model in order to reproduce these motions. I will quickly summarize things here: Ptolemy’s model did not simply have the planets and the Sun attached to one sphere each, but he had to adopt circles (epicycles) on top of circles (deferents) with the Earth offset from the center. The most complex version of the model was still often in error in its predictions by several degrees, or by an angular distance larger than the diameter of the full Moon.
Want to learn more?
This is an interesting topic I won't describe in any more detail, but if you would like to learn more, there is much more about the Ptolemaic model in most introductory astronomy textbooks, including the online Astronomynotes.com [14].
There is a faculty member at Florida State who has made animated models of the Ptolemaic system: in the first movie below, you can see how the Moon and Sun were conceptualized to have orbited Earth. In the second movie, you can see how Mercury and the Sun were conceptualized to have orbited Earth.
Recall that the Greeks did rely on mathematical reasoning when conducting experiments and designing their models. You may wonder, in the Greek model, what order were the "planets" out from the Earth, and how were they chosen to be in that order? The order was:
- Earth (unmoving; located at the center)
- Moon
- Mercury
- Venus
- Sun
- Mars
- Jupiter
- Saturn
We will discuss this concept more later, but consider the angular speed of an object on the sky. The faster the angular speed, the larger the angular distance an object will cover in the same amount of time. A simple example is to consider two airplanes on the sky. One is close to you, and the other more distant. If both planes are flying at the same speed in the same direction across your line of sight, the more distant airplane will appear to cover a shorter angular distance on the sky than the nearby plane. So, if you can estimate the angular speed of two objects and if you assume that they are moving at the same real speed and in the same direction, the one that travels the shorter distance on the sky must be the more distant object.
The Greeks used this method to estimate the distance to the planets, and they were able to determine the relative ordering of the planets. The most significant flaw was their assumption of the Earth as the center of all things.
The Heliocentric Model
Additional reading at www.astronomynotes.com [1]
The geocentric model of the Solar System remained dominant for centuries. However, because even in its most complex form it still produced errors in its predictions of the positions of the planets in the sky, some astronomers continued to search for a better model.
The astronomer given the credit for presenting the first version of our modern view of the Solar System is Nicolaus Copernicus, who was an advocate for the heliocentric, or Sun-centered model of the solar system. Copernicus proposed that the Sun was the center of the Solar System, with all of the planets known at that time orbiting the Sun, not the Earth. Although this solved many longstanding problems in the Ptolemaic model, Copernicus still believed that the orbits of planets must be circular, and so his model was not much more successful than Ptolemy’s in predicting the position of the planets. His model was very successful, however, in solving the problem of retrograde motion in a very elegant manner. This is illustrated in the video Retrograde Motion (6 minutes, 25 seconds).
In the night sky, stars rise and set due to the rotation of Earth. However, the pattern of stars that is seen in the sky, how far apart a pair of stars are seen from each other, stays the same over time scales of thousands of years. However, planets move in the sky relative to the pattern of background stars. They change their position in the sky from night to night. The term “planet” originates from the Greek word for “wanderer.” This phenomenon can’t be really be seen on any given night. But if you note the location of a planet relative to the background stars, and note its location again several nights later, you will see that it has moved. This could be seen if you took a series of photos every night for a month with a chosen star highest in the sky and laid them over the top of each other. Planets typically move eastward, the direction of increasing right ascension, which we know today is due to their revolution around the sun. Note that a planet still rises in the east and sets in the west on any given night due to the rotation of Earth. This video will focus on a variation of that motion known as retrograde motion. This apparent motion concerns the planet slowing in its eastward motion, stopping, moving westward for a while, and stopping again before continuing on its eastward journey. For superior planets, those that orbit the sun further out than Earth, and the only planets that will be discussed in this video, this effectively creates a loop in the sky.
Two thousand years ago, the Greek astronomer Ptolemy explained retrograde motion with a geocentric system of wheels within wheels, kind of like the kids’ drawing game Spirograph. It was believed that Earth was at the center of everything and that a planet moved on a circular path called an epicycle, the center of which moved on a larger circle called the deferent. This allowed the existence of retrograde loops to be explained, although in a complicated way. We know today that this explanation was completely wrong.
In the 1500s, Copernicus explained retrograde motion with a far more simple, heliocentric theory that was largely correct. Retrograde motion was simply a perspective effect caused when Earth passes a slower moving outer planet that makes the planet appear to be moving backwards relative to the background stars. Thus, retrograde motion occurs over the time when the sun, Earth, and planet are aligned, and the planet is described as being at opposition – opposite the sun in the sky. This is why retrograde motion is referred to as “apparent retrograde motion” by many. Nothing is changing in the planet’s motion, and retrograde motion occurs as a natural perspective effect. Let’s look at a demonstration for teaching retrograde motion. It consists of the sun at the center, in red. Earth and a superior planet in a circular orbit around it. Here, a white rod connects Earth and a superior planet similar to Mars and represents the perspective, pointing to the location where Mars would be seen in the sky from Earth. East is counter-clockwise around this circle. A system of circular gears controls the positions of Earth and Mars and their rates of motion.
A hand crank allows the demonstrator to advance Earth and Mars, while the gears ensure appropriate relative rates. Note that an arrow illustrates the direction of apparent motion in the sky. And we have placed background stars around the edge where we will see the apparent position of Mars. We start our demonstration several months before Mars reaches opposition. Remember that Earth is moving faster than Mars and will shortly overtake it. The rod connecting Earth to Mars points to Mars’ apparent position in the sky.
As we turn the crank slowly to advance time, Mars is initially moving eastwards. We have now reached the point where Mars’ eastward motion appears to stop, the beginning of retrograde motion. Note that Mars is now moving westward. Mars reaches opposition at the middle of retrograde motion. We have now reached the point where Mars’ westward motion appears to cease. The end of retrograde motion. As we continue to advance time, Mars resumes its normal eastward motion relative to the stars. Note that this effect is entirely due to perspective. Nothing changed in the motions of Mars or Earth.
This diagram illustrates the perspective effect that underlies retrograde motion.
At which (lettered) location in the sky does a superior planet appear to be located for the planet and earth locations indicated? Please record your vote on a piece of paper and explain your method for determining your answer.
To determine the apparent location of the planet in the sky, one would simulate a line of sight by drawing a line from earth through the planet into the surrounding sky.
Let’s finish up by discussing the general characteristics of retrograde motion.
The table below shows several values describing the retrograde motion of superior planets. The table provides the synodic period. This is how often Earth passes a superior planet, the time from one opposition to another, so it is also the time interval between retrograde motions. Note that as one considers planets in larger orbits, the synodic period gets closer and closer to one year. In fact, for the planet “Far Out,” which is in a very large orbit, the synodic period would be exactly one year, as it would orbit so slowly that it would effectively not move. Correspondently, the retrograde interval, the time spent moving westwards is smallest for Mars, and grows to half a year for our “Far Out” planet. Note that the size of the retrograde loop, the angular extent of the backwards moving tract in the sky, is largest for Mars and decreases to zero for the “Far Out” planet. This can be understood in terms of our change in perspective. Mars is the closest planet to Earth and thus moves the most during the time that it takes Earth to pass it. Thus, it can appear to be in the largest range of positions. The perspective effect is largest.
More teaching materials can be found on the web at astro.unl.edu
Test this with Starry Night!
Note also that you can reproduce the animation (but without the arrows) with Starry Night! This is a bit more tricky, but here are the steps:
- Instead of choosing a location on Earth or on Mars, you can choose a stationary location. In this case, you want to be floating above the Sun, so you can set the location to X = 0, Y = 0, and Z = 1 billion miles (or in Astronomical Units, 10 AU).
- Choose to label planets and moons from the labels menu
- If you do not see the Sun and planets, search for the Sun in the find menu and double click on the word "Sun" when it comes up
- Right click on Earth and Mars and choose "orbit"
- Set the time step to days; press play
You can now watch the orbits of Earth and Mars on a given set of dates to choose when Earth is overtaking Mars, and then you can reset things so you are watching the sky from Earth on that same date and watch Mars go through a retrograde loop! I have not created a Starry Night file for this example, but please let me know if you would like one.
Starry Night does have some built in "Favorites". They do have a similar one for the inner Solar System. In the Favorites menu, choose Solar System, then Inner Planets, and then Inner Solar System, and it will show you a view of the Inner Solar System slightly different from the one you will see if you follow the instructions above. You can also get to this Favorite by clicking on the "hamburger menu" (the three horizontal lines) on the right side of the top status bar.
Although Copernicus’ model solved some problems, its lack of accuracy in predicting planetary positions kept it from becoming widely accepted as better than the Ptolemaic model. The advocates for the Geocentric model also proposed another test for the heliocentric model: if the Earth is orbiting the Sun, then the distant stars should appear to shift from our point of view, an effect known as parallax. We will study parallax in more detail in a later lesson on stars. However, for now I will note that this caused a problem for advocates of the heliocentric model. If they were right, we should observe parallax, but not even the most accurate observers of the day were able to detect a measurable amount of parallax for even a single star.
Forgetting parallax for a moment, the advances necessary to increase the acceptance of the heliocentric model came from Tycho Brahe and Johannes Kepler. Brahe is credited with being one of the best observers of his time. At his observatory, and over approximately 15 years, using instruments he designed and built, Brahe compiled a continuous list of accurate positions for the planets on the sky. Johannes Kepler came to work with Brahe shortly before Brahe died. Kepler used his mathematical skill to study the accurate observations of Brahe and then proposed three laws that accurately describe the motions of the planets in the solar system.
Kepler's Three Laws
Additional reading at www.astronomynotes.com [8]
First Law
Kepler was a sophisticated mathematician, and so the advance that he made in the study of the motion of the planets was to introduce a mathematical foundation for the heliocentric model of the solar system. Where Ptolemy and Copernicus relied on assumptions, such as that the circle is a “perfect” shape and all orbits must be circular, Kepler showed that mathematically a circular orbit could not match the data for Mars, but that an elliptical orbit did match the data! We now refer to the following statement as Kepler’s First Law:
- The planets orbit the Sun in ellipses with the Sun at one focus (the other focus is empty).
For more information about ellipses, you can read in gory mathematical detail the page hosted at Mathworld [19], and there is also information on ellipses in Wikipedia [20].
Here is a demonstration of the classic method for drawing an ellipse:
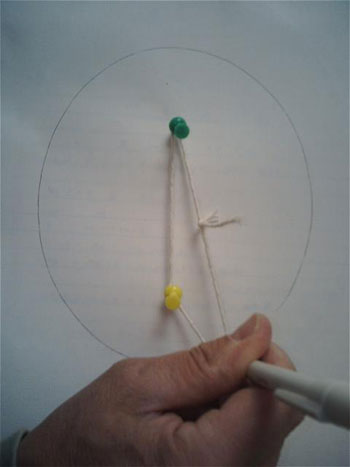
The two thumbtacks in the image represent the two foci of the ellipse, and the string ensures that the sum of the distances from the two foci (the tacks) to the pencil is a constant. Below is another image of an ellipse with the major axis and minor axis defined:
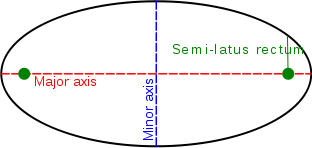
We know that in a circle, all lines that pass through the center (diameters) are exactly equal in length. However, in an ellipse, lines that you draw through the center vary in length. The line that passes from one end to the other and includes both foci is called the major axis, and this is the longest distance between two points on the ellipse. The line that is perpendicular to the major axis at its center is called the minor axis, and it is the shortest distance between two points on the ellipse.
In the image above, the green dots are the foci (equivalent to the tacks in the photo above). The larger the distance between the foci, the larger the eccentricity of the ellipse. In the limiting case where the foci are on top of each other (an eccentricity of 0), the figure is actually a circle. So you can think of a circle as an ellipse of eccentricity 0. Studies have shown that astronomy textbooks introduce a misconception by showing the planets' orbits as highly eccentric in an effort to be sure to drive home the point that they are ellipses and not circles. In reality the orbits of most planets in our Solar System are very close to circular, with eccentricities of near 0 (e.g., the eccentricity of Earth's orbit is 0.0167). For an animation showing orbits with varying eccentricities, see the eccentricity diagram [23] at "Windows to the Universe." Note that the orbit with an eccentricity of 0.2, which appears nearly circular, is similar to Mercury's, which has the largest eccentricity of any planet in the Solar System. The elliptical orbits diagram [24] at "Windows to the Universe" includes an image with a direct comparison of the eccentricities of several planets, an asteroid, and a comet. Note that if you follow the Starry Night instructions on the previous page to observe the orbits of Earth and Mars from above, you can also see the shapes of these orbits and how circular they appear.
Kepler’s first law has several implications. These are:
- The distance between a planet and the Sun changes as the planet moves along its orbit.
- The Sun is offset from the center of the planet’s orbit.
Second Law
In their models of the Solar System, the Greeks held to the Aristotelian belief that objects in the sky moved at a constant speed in circles because that is their “natural motion.” However, Kepler’s second law (sometimes referred to as the Law of Equal Areas), can be used to show that the velocity of a planet changes as it moves along its orbit!
Kepler’s second law is:
- The line joining the Sun and a planet sweeps through equal areas in an equal amount of time.
The image below links to an animation that demonstrates that when a planet is near aphelion (the point furthest from the Sun, labeled with a B on the screen grab below) the line drawn between the Sun and the planet traces out a long, skinny sector between points A and B. When the planet is close to perihelion (the point closest to the Sun, labeled with a C on the screen grab below), the line drawn between the Sun and the planet traces out a shorter, fatter sector between points C and D. These slices that alternate gray and blue were drawn in such a way that the area inside each sector is the same. That is, the sector between C and D on the right contains the same amount of area as the sector between A and B on the left.
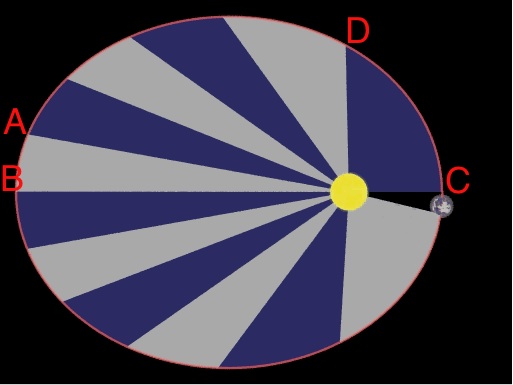 [25]
[25]
Kepler's 2nd Law
Since the areas of these two sectors are identical, then Kepler's second law says that the time it takes the planet to travel between A and B and also between C and D must be the same. If you look at the distance along the ellipse between A and B, it is shorter than the distance between C and D. Since velocity is distance divided by time, and since the distance between A and B is shorter than the distance between C and D, when you divide those distances by the same amount of time you find that:
- A planet is moving faster near perihelion and slower near aphelion.
The orbits of most planets are almost circular, with eccentricities near 0. In this case, the changes in their speed are not too large over the course of their orbit.
For those of you who teach physics, you might note that really, Kepler's second law is just another way of stating that angular momentum is conserved. That is, when the planet is near perihelion, the distance between the Sun and the planet is smaller, so it must increase its tangential velocity to conserve angular momentum, and similarly, when it is near aphelion when their separation is larger, its tangential velocity must decrease so that the total orbital angular momentum is the same as it was at perihelion.
Third Law
Kepler had all of Tycho’s data on the planets, so he was able to determine how long each planet took to complete one orbit around the Sun. This is usually referred to as the period of an orbit. Kepler noted that the closer a planet was to the Sun, the faster it orbited the Sun. He was the first scientist to study the planets from the perspective that the Sun influenced their orbits. That is, unlike Ptolemy and Copernicus, who both assumed that the planet's “natural motion” was to move at constant speeds along circular paths, Kepler believed that the Sun exerted some kind of force on the planets to push them along their orbits, and because of this, the closer they are to the Sun, the faster they should move.
Kepler studied the periods of the planets and their distance from the Sun, and proved the following mathematical relationship, which is Kepler’s Third Law:
- The square of the period of a planet’s orbit (P) is directly proportional to the cube of the semimajor axis (a) of its elliptical path.
What this means mathematically is that if the square of the period of an object doubles, then the cube of its semimajor axis must also double. The proportionality sign in the above equation means that:
where k is a constant number. If we divide both sides of the equation by , we see that:
This means that for every planet in our solar system, the ratio of their period squared to their semimajor axis cubed is the same constant value, so this means that:
We know that the period of the Earth is 1 year. At the time of Kepler, they did not know the distances to the planets, but we can just assign the semimajor axis of the Earth to a unit we call the Astronomical Unit (AU). That is, without knowing how big an AU is, we just set . If you plug 1 year and 1 AU into the equation above, you see that:
So for every planet, if P is expressed in years and a is expressed in AU. So if you want to calculate how far Saturn is from the Sun in AU, all you need to know is its period. For Saturn, this is approximately 29 years. So:
So Saturn is 9.4 times further from the Sun than the Earth is from the Sun!
Newtonian Gravitation
Additional reading at www.astronomynotes.com [1]
Kepler's Laws are sometimes referred to as "Kepler's Empirical Laws." The reason for this is that Kepler was able to mathematically show that the positions of the planets in the sky were fit by a model that required orbits to be elliptical, the velocity of the planets in orbit to vary, and that there is a mathematical relationship between the period and the semimajor axis of the orbits. Although these were remarkable accomplishments, Kepler was unable to come up with an explanation for why his laws were true—that is, why are orbits elliptical and not circular? Why does the period of a planet determine the length of its semimajor axis?
Isaac Newton is given credit for explaining, theoretically, the answers to these questions. In his most famous work, the Principia, Newton presented his three laws:
- An object at rest or in motion in a straight line at a constant speed will remain in that state unless acted upon by a force.
- The acceleration of a body due to a force will be in the same direction as the force, with a magnitude indirectly proportional to its mass. (This is usually written as ).
- For every action, there is an equal and opposite reaction.
In addition, he presented his law of universal gravitation:
- The force of gravity between two masses is:
That is, the force of gravity depends on both their masses, a constant (G), and it drops off as 1 over the distance squared. In this equation, d, the distance, is measured from the center of the object. That is, if you want to know the force of gravity on you from the Earth, you should use the radius of the Earth as d, since you are that far away from the center of the Earth.
Using these laws and the mathematical techniques of calculus (which Newton invented), Newton was able to prove that the planets orbit the Sun because of the gravitational pull they are feeling from the Sun. The way an orbit works is as follows (this is a thought experiment attributed to Newton, sometimes called Newton's cannon):
Think of a cannon on a high mountain near the north pole of the Earth. If you were to shoot a cannonball horizontally, parallel to the Earth's surface, it would drop vertically towards the Earth's surface at the same time it is moving horizontally away from the mountain, and eventually hit the Earth. If you shot the cannonball with more force, it would travel farther from the mountain before it hit the Earth. Well, what would happen if you shot the cannonball with so much force that the amount of the vertical drop of the cannonball towards the surface due to Earth's gravity was the same magnitude as the Earth's dropoff because of its spherical shape? That is, if you could shoot a projectile with enough force, it would fall towards the Earth like any other projectile, but it would always miss hitting the Earth! For an example of this, see this Applet of Newton's cannon [28].
Although the Earth was never shot out of a cannon, the same physics applies. Think of the Earth sitting at the 3 o'clock position in its orbit around the Sun. If the Earth were to just freely fall through space without experiencing any force, by Newton's first law, it would just continue to fall in a straight line. However, the Sun is pulling on the Earth such that the Earth feels a tug towards the Sun. This causes the Earth to also fall towards the Sun a bit. The combination of the Earth falling through space and it perpetually being tugged a little bit in the direction of the Sun causes it to follow a roughly circular path around the Sun. This effect can be illustrated in the following animation:
This animation shows the Earth moving along its orbit around the Sun. It labels the tangential velocity of the Earth with a red arrow that is tangential to Earth's orbit. It also labels the force of gravity with a blue arrow pulling Earth towards the Sun, which is perpendicular to the tangential velocity of the Earth. (Notice that in accordance with Newton's Third Law, there is an equal and opposite force of the Earth on the Sun, also a blue arrow.) The combination of these two factors - Earth's tangential velocity and force due to gravity - causes the Earth to accelerate and follow an elliptical (albeit nearly circular) path around the Sun.
I should note here that this concept requires thinking about the concept of inertia, which can be very confusing, and, in fact, this particular animation uses terminology that may reinforce this confusion. There is no "Force of Inertia"; inertia is not a force. Instead, the proper way to think about this is that inertia is the property of an object that determines how strongly it resists changing its motion. So, picture a planet moving in a straight line; it has a lot of inertia, because a large, massive planet is hard to move off of that straight line. However, the Sun pulls on that planet with the force of gravity, and that gravitational pull is strong enough to divert the planet from a straight line path. If the tangential velocity of the planet is balanced by the change in velocity introduced by gravity, you get a stable orbit.
Try this!
The PHeT simulations [29] include two that allow you to play with orbital motion. One is called "Gravity and Orbits" and the other is called "My Solar System". You can set up initial conditions for planets and a star, and then see what happens.
- Can you create a stable orbit?
- Can you alter a stable orbit so that it is no longer stable? If so, what did you do?
- What happens to objects on unstable orbits?
Using the techniques of calculus, you can actually derive all of Kepler's Laws from Newton's Laws. That is, you can prove that the shape of an orbit caused by the force of gravity should be an ellipse. You can show that the velocity of an object increases near perihelion and decreases near aphelion, and you can show that . In fact, Newton was able to derive the value for the constant, k, and today we write Newton's version of Kepler's Third Law this way:
Which means that
If we use Newton's version of Kepler's Third Law, we can see that if you can measure P and measure a for an object in orbit, then you can calculate the sum of the mass of the two objects! For example, in the case of the Sun and the Earth, , so just by measuring , you can calculate !
This is the basis of a lab we are going to do during this unit. You are going to find P and a for several of Jupiter's Moons, and you are going to use those data to calculate the mass of Jupiter.
Lastly, I would like everyone to do a quick calculation using the formula for Newton's Law of Universal Gravitation:
For now, we can ignore the constant G. We are going to calculate a ratio, so in the end the constant will drop out. What I want us to look at is the force of gravity "in space." That is, for astronauts in the space shuttle or in the International Space Station (ISS), how does the force of gravity from Earth that they feel compare to the force of gravity that you feel sitting here on Earth?
If you are unfamiliar with doing ratios, do the following step by step:
- Write out this equation one time for the situation on Earth, that is:
- Write out this equation a second time for the situation in Space, that is:
- Form a ratio taking the equation from #1 above and putting it over #2 above, that is:
At this point, if you recall from the rules of algebra, when you have quantities on the top and bottom of a fraction that are the same, they cancel out. So, you can cross out everything on the right hand side you find on both the top and bottom, that is, G, m1, and m2.
You are then left with:
What this tells you is that the ratio between the force of gravity you feel on Earth to the force of gravity you feel in space is only related to the distance between Earth and you in both cases. In case 1, when you are on Earth, you would fill in the radius of the Earth, approximately 6400 km. The space shuttle and the ISS do not orbit far from Earth. A reasonable number for the distance between the surface of Earth and the ISS is about 350 km. So, the distance between the Earth and the ISS for calculating the force of gravity on the ISS is . Fill in these values for and calculate this ratio. This will give you an answer for how much stronger the gravity is on the surface of Earth compared to in the ISS.
Additional Resources
- I tend not to focus too much on the historical figures in astronomy and their accomplishments, and I left out a lot about Galileo, who was very important in the transition from a Geocentric to Heliocentric view of the Universe. If you'd like to read more about Galileo on your own, I recommend the Galileo Project. [30]
- In the ClassAction Modules [31] there are modules related to this unit under Basic Motions & Ancient Astronomy and Renaissance Astronomy. I recommend the Renaissance Astronomy module called the "Planetary Orbit Simulator," and they also have modules similar to the ones in this lesson (e.g., the retrograde motion animation).
- On Teacher's Domain, there are several resources related to this lesson:
- A video from NASA [32] of the Galileo Experiment performed on the Moon.
- A video about a classroom demo you can do on weightlessness [33].
- A NOVA animation about Newton's cannon and weightlessness [34].
- In the lesson, I recommended the PhET simulations [35] and suggested you try experimenting to create stable and unstable orbits using one of their orbital simulators. A physics teacher collaborator and I wrote an article about an in-class investigation you can do with one of those simulations, and it is available for free in PDF form here: Earth Scientist Vol XXIX Summer 2013 [36] (see p. 32)
Tell us about it!
Have another website on this topic that you have found useful? Share it in the Comment area!
Summary & Final Tasks
In this lesson, you learned how astronomy went from a careful study of the sky to a science with a basis in the fundamental laws of physics. While in an astronomy course, we are forced to gloss over a lot of the physics of Newton's Laws, I do hope that you come away with an appreciation for the physics of orbits and a firm understanding that there is gravity in space.
Activity 1
Directions
First, please take the Web-based Lesson 2 quiz.
- Go to Canvas.
- Go to the "Lesson 2 Quiz" and complete the quiz.
Good luck!
Activity 2
Directions
There is a second quiz for this lesson that contains several short math problems. While I expect you to complete the quiz and to give it the same effort you would for a graded assignment, for these problems you will only be graded on completion and not on the accuracy of your answers. Your participation in this quiz will count in lieu of a discussion forum for this lesson.
- Go to Canvas.
- Go to the "Lesson 2 Practice Problems" and complete the quiz.
Activity 3
Directions
During this week, you should begin work on the lab exercise that will be completed and submitted next week.
- Lab 1 is located on the next page.
- Read the background information, and then follow the instructions for taking data with the simulated Moons of Jupiter.
- Take data and record it as instructed.
Reminder - Complete all of the lesson tasks!
You have finished the reading for Lesson 2. Double-check the list of requirements on the Lesson 2 Overview page to make sure you have completed all of the activities listed there before beginning the next lesson.
Lab 1
Lab 1: Observing Jupiter's Moons
Used with permission from "Engaging in Astronomical Inquiry", by Stephanie Slater, Timothy Slater, and Daniel Lyons. Copyright W.H. Freeman and Company, New York, 2010
Big Idea
Sky objects have properties, locations, and predictable patterns of movements that can be observed and described.
Goal
Students will conduct a series of inquiries about the position and motion of Jupiter’s moons using prescribed Internet simulations.
Computer Setup and/or Materials Needed:
Access NASA Jet Propulsion Laboratory - California Institute of Technology: Solar System Simulator [37] and
a) Select THE MOON in the “Show me _______ “ drop down menu
b) Select THE SUN in the “as seen from _______ “ drop down menu
c) Select the radio button “I want a field of view of ____ degrees” and set the drop down menu to 0.5
d) UNCHECK all the "Options" check boxes except for EXTRA BRIGHTNESS (**this makes it easier to see!!**)
e) Click “Run Simulator”
Phase I: Exploration
After completing the above steps, answer the following questions. If you are taking the course for credit, complete the open-ended responses within the 'Lab 1' Module link in Canvas.
1. The resulting image shows what one would see looking through a special telescope. In this picture, where is the observer with the special telescope located?
2. How does the image change if you INCREASE the field of view?
3. What is the exact date of the image?
4. Astronomers typically mark images based on the time it currently is in Greenwich, England, called UTC. What is the precise time listed on the image?
5. Using a ruler to measure the distance on the screen between the middle of Earth and the middle of the Moon, what is the measured distance? You do NOT need to know the exact number of kilometers, but simply a ruler-measurement you can compare with other measurements you make later. Alternately, you can use the edge of a piece of lined paper held in the landscape orientation and count the lines, or mark the locations of Earth and Moon along the edge of a piece of blank paper and hold the paper up next to the arbitrary "Squigit" ruler (Links to an external site.) [38] (Note: ruler pops up in a different window. WARNING: This window is resizable, so be sure not to resize the squigit ruler window AFTER you have begun using it!) to get a measurement. You will be making many measurements in this lab, so pick a method that is efficient for you and allows reasonable precision and accuracy.
6. In the measurement you just took, which side of the Earth was the Moon on: Enter either "L", "R" or "N/A" (if the Moon was behind the Earth)?
7. Use the browser’s BACK button to return to the Solar System Simulator homepage. Now, advance the time by 1 hour and determine the new distance between the Earth and Moon.
8. In the measurement you just took, which side of the Earth was the Moon on: "L", "R" or "N/A" (if the Moon was behind the Earth)?
9. Use the browser’s BACK button to return to the Solar System Simulator homepage. Now, advance the time by one day from when you started and determine the new distance between the Earth and Moon.
10. In the measurement you just took, which side of the Earth was the Moon on: "L", "R" or "N/A" (if the Moon was behind the Earth)?
11. Use the browser’s BACK button to return to the Solar System Simulator homepage. Now, advance the time by three days from when you started and determine the new distance between the Earth and Moon.
12. In the measurement you just took, which side of the Earth was the Moon on: "L", "R" or "N/A" (if the Moon was behind the Earth)?
13. Use the browser’s BACK button to return to the Solar System Simulator homepage. Now, advance the time by five days from when you started and determine the new distance between the Earth and Moon.
14. In the measurement you just took, which side of the Earth was the Moon on: "L", "R" or "N/A" (if the Moon was behind the Earth)?
15. Use the browser’s BACK button to return to the Solar System Simulator homepage. Now, advance the time by 10 days from when you started and determine the new distance between the Earth and Moon.
16. In the measurement you just took, which side of the Earth was the Moon on: "L", "R" or "N/A" (if the Moon was behind the Earth)?
17. Use the browser’s BACK button to return to the Solar System Simulator homepage. Now, advance the time by two weeks from when you started and determine the new distance between the Earth and Moon. Be sure to include left or right.
18. In the measurement you just took, which side of the Earth was the Moon on: "L", "R" or "N/A" (if the Moon was behind the Earth)?
19. Use the browser’s BACK button to return to the Solar System Simulator homepage. Now, advance the time by one month from when you started and determine the new distance between the Earth and Moon.
20. In the measurement you just took, which side of the Earth was the Moon on: "L", "R" or "N/A" (if the Moon was behind the Earth)?
21. Use the browser’s BACK button to return to the Solar System Simulator homepage. Now, advance the time by three months from when you started and determine the new distance between the Earth and Moon.
22. In the measurement you just took, which side of the Earth was the Moon on: "L", "R" or "N/A" (if the Moon was behind the Earth)?
23. Consider the research question of, “how long does it take the Moon to orbit Earth?” It has been said that it takes about one “moon-th” for the Moon to go around Earth. Which of your observations confirms or contradicts this statement? Explain.
Phase II: Does the Evidence Match a Given Conclusion?
24. Consider the research question, “How long does it take one of Jupiter’s moons to orbit Jupiter?” Set the Solar System Simulator to observe Jupiter from the Sun, where Jupiter takes up 10% of the image, and measure the distance between Jupiter and Io shown on the image
25. In the measurement you just took, which side of Jupiter was Io on: "L", "R" or "N/A" (if the Io was behind Jupiter)?
26. Advance the “time” by one day, and record the distance between Jupiter and Io.
27. In the measurement you just took, which side of Jupiter was Io on: "L", "R" or "N/A" (if the Io was behind Jupiter)?
28. Advance the “time” by two days from when you started, and record the distance between Jupiter and Io.
29. In the measurement you just took, which side of Jupiter was Io on: "L", "R" or "N/A" (if the Io was behind Jupiter)?
30. Advance the “time” by three days from when you started, and record the distance between Jupiter and Io.
31. In the measurement you just took, which side of Jupiter was Io on: "L", "R" or "N/A" (if the Io was behind Jupiter)?
32. Advance the “time” by four days from when you started, and record the distance between Jupiter and Io.
33. In the measurement you just took, which side of Jupiter was Io on: "L", "R" or "N/A" (if the Io was behind Jupiter)?
34. Advance the “time” by five days from when you started, and record the distance between Jupiter and Io.
35. In the measurement you just took, which side of Jupiter was Io on: "L", "R" or "N/A" (if the Io was behind Jupiter)?
36. Advance the “time” by six days from when you started, and record the distance between Jupiter and Io.
37. In the measurement you just took, which side of Jupiter was Io on: "L", "R" or "N/A" (if the Io was behind Jupiter)?
38. If a fellow student proposed a generalization that "Io orbits the Jupiter about every 48 hours," would you agree or disagree with the generalization based on the evidence you collected by noting patterns in the time it takes for Io to return to its original position from where it started? Explain your reasoning and provide specific evidence either from the above tasks or from new evidence you yourself generate using the Solar System Simulator. It is not enough to vaguely reference "the answers to the questions above" - you need to cite specific numeric evidence and explain how it supports your answer.
Phase III: What Conclusions can you draw from this Evidence?
39. Europa is one of the four largest moons orbiting Jupiter. The others are Io, Callisto, and Ganymede. What conclusions and generalizations can you make from the following data collected by a student in terms of HOW LONG DOES IT TAKE EUROPA TO ORBIT JUPITER? Explain your reasoning and provide specific evidence, with sketches if necessary, to support your reasoning.
| Time | Measured Distance from Jupiter | Appearance Notes |
|---|---|---|
| 11pm Monday | 0 squidgets | Not visible, likely behind Jupiter |
| 11pm Tuesday | 5.0 squidgets | On Jupiter's right side |
| 11pm Wednesday | 1.5 squidgets | On Jupiter's right side |
| 11pm Thursday | 5.0 squidgets | On Jupiter's left side |
| 11pm Friday | No observations | cloudy |
Remember, a picture is worth 103 words! Optional: Feel free to create and label sketches or graphs to illustrate your response. Please upload any sketches/graphs. (Please do not email your file to the instructor.)
Phase IV: What Evidence do you need?
40. Imagine your team has been assigned the task of writing a news brief for your favorite news blog about the length of time it takes Ganymede, the largest moon in the entire solar system, to orbit Jupiter once. Describe precisely what evidence you would need to collect, and how you would do it, in order to answer the research question of, "Over what precise period of time does it take Ganymede to orbit Jupiter?" You do not need to actually complete the steps in the procedure you are writing.
Write a Procedure: Create a detailed, step-by-step description of evidence that needs to be collected and a complete explanation of how this could be done - not just "look and see when the Ganymede is first on one side and then on the other", but exactly what would someone need to do, step-by-step, to accomplish this. You might include a table and sketches - the goal is to be precise and detailed enough that someone else could follow your procedure. Do NOT include generic nonspecific steps such as "analyze data" or "present conclusions" -- these are meaningless filler. Be specific! Remember, a picture is worth 103 words! Optional: Feel free to create and label sketches or graphs to illustrate your response.
Phase V: Formulate a Question, Pursue Evidence, and Justify Your Conclusion
Your task is to design an answerable research question, propose a plan to pursue evidence, collect data using using Solar System Simulator (or another suitable source pre-approved by your instructor), and create an evidence-based conclusion about some motion or changing position of a moon or planet of the solar system, that you have not completed before. Remember, a picture is worth 103 words! Optional: Feel free to create and label sketches or graphs to illustrate your response. Please upload all sketches/graphs here. (Please do not email your file to the instructor.)
Research Report:
41. Write your specific research question.
42. Write your step-by-step procedure, with sketches if needed, to collect evidence. (Do NOT include generic nonspecific steps such as "analyze data" or "present conclusions" -- these are meaningless filler. Be specific!)
43. Provide your data table and/or results.
44. Provide your evidence-based conclusion statement.
Phase VI: Summary
45. Create a PITHY 50-word summary, in your own words, that describes the motions, orbits, or rotations of Jupiter’s moons (or other moons or planets in our solar system that you might have studied). You should cite what you learned from doing each of the phases of this lab, not describe what you have learned in class or elsewhere. Include a word count at the end of your answer. (Remember, 50 words is not much! This is intended to keep you mindful of making your answers BRIEF and PITHY.)
Submit your work in Lesson 3
This lab assignment is not due in Canvas until the due date indicated on our course calendar during Lesson 3.
