Blackbody Radiation
Additional reading from www.astronomynotes.com [1]
First, let's do a quick review of temperature scales and the meaning of temperature. The temperature of an object is a direct measurement of the energy of motion of atoms and/or molecules. The faster the average motion of those particles (which can be rotational motion, vibrational motion, or translational motion), the higher the temperature of the object.
For this course, to keep with astronomical convention, we'll refer to temperatures using the Kelvin scale. The following is a table that compares kelvin to the more familiar temperature scales:
| Celsius | Fahrenheit | Kelvin | |
|---|---|---|---|
| All molecular motion stops | -273 | -459 | 0 |
| Freezing point of water | 0 | 32 | 273 |
| Boiling point of water | 100 | 212 | 373 |
The magnitude of one degree Celsius is the same as one K. The only difference between those two scales is the zero point.
Part of the reason for this quick review of temperature is because we are now going to begin studying the emission of light by different bodies, and all objects with temperatures above absolute zero give off light.
Our strategy will be to begin by studying the properties of the simplest type of object that emits light, which is called a blackbody. A blackbody is an object that absorbs all of the radiation that it receives (that is, it does not reflect any light, nor does it allow any light to pass through it and out the other side). The energy that the blackbody absorbs heats it up, and then it will emit its own radiation. The only parameter that determines how much light the blackbody gives off, and at what wavelengths, is its temperature. There is no object that is an ideal blackbody, but many objects (stars included) behave approximately like blackbodies. Other common examples are the filament in an incandescent light bulb or the burner element on an electric stove. As you increase the setting on the stove from low to high, you can observe it produce blackbody radiation; the element will go from nearly black to glowing red hot.
The temperature of an object is a measurement of the amount of random motion (the average speed) exhibited by the particles that make up the object; the faster the particles move, the higher the temperature we will measure. If you recall from the very beginning of this lesson, we learned that when charged particles are accelerated, they create electromagnetic radiation (light). Since some of the particles within an object are charged, any object with a temperature above absolute zero (0 K or –273 degrees Celsius) will contain moving charged particles, so it will emit light.
A blackbody, which is an “ideal” or “perfect” emitter (that means its emission properties do not vary based on location or the composition of the object), emits a spectrum of light with the following properties:
- The hotter the blackbody, the more light it gives off at all wavelengths. That is, if you were to compare two blackbodies, regardless of what wavelength of light you observe, the hotter blackbody will give off more light than the cooler one.
- The spectrum of a blackbody is continuous (it gives off some light at all wavelengths), and it has a peak at a specific wavelength. The peak of the blackbody curve in a spectrum moves to shorter wavelengths for hotter objects. If you think in terms of visible light, the hotter the blackbody, the bluer the wavelength of its peak emission. For example, the sun has a temperature of approximately 5800 Kelvin. A blackbody with this temperature has its peak at approximately 500 nanometers, which is the wavelength of the color yellow. A blackbody that is twice as hot as the sun (about 12000 K) would have the peak of its spectrum occur at about 250 nanometers, which is in the UV part of the spectrum.
Here is a two-dimensional plot of the spectrum of a blackbody with different temperatures:
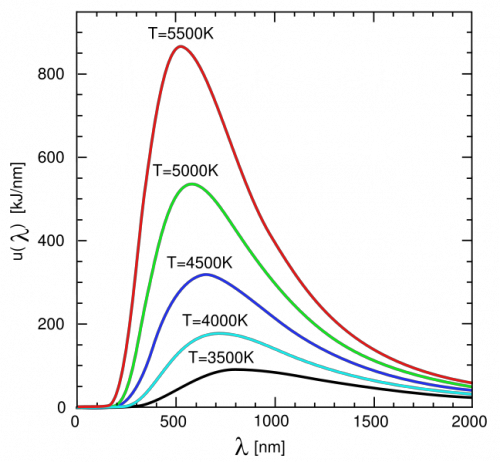
The first of the two properties listed above (and seen in the image above) is usually referred to as the Stefan-Boltzmann Law and is stated mathematically as:
where:
E is the energy emitted per unit area, or intensity,
is a constant, and
T is the temperature (measured in Kelvins).
What this equation tells you is that each time you double the temperature of a blackbody, the energy it emits per square centimeter goes up by . So, for example, a blackbody that is 5000 K emits 16 times more energy per unit area than one that is 2500 K.
The total luminosity of a blackbody, that is, how much energy the entire object gives off, is the energy per unit area (E) multiplied by the surface area. For a sphere, this is:
Here, L is the luminosity (energy per unit time) and R is the radius of the sphere.
The second of the two properties listed above is referred to as Wien's Law. To determine the peak wavelength of the spectrum of a blackbody, the equation is:
For example, for the sun,
Try This!
There is an online, interactive tool from the University of Colorado for investigating the spectrum of various blackbodies. Here is the link to run it online: PhET Interactive Simulation of the Blackbody Spectrum [4].
- Using the temperature slider, set the temperature to 3000 K (light bulb), 5700 K (Sun), and 8490 K (hot star).
- Use the zoom in and zoom out controls on the left side to adjust the y-axis as necessary.
- Compare the color of the object (the star-shaped object near the B G R color spots), the wavelength where the curve peaks, and the height of the curve's peak for all three temperatures.