Systems Thinking and the Hydrologic Cycle
Systems Thinking and the Hydrologic Cycle
Throughout this course, we will be dealing with complex systems and “Systems Thinking”. What is Systems Thinking, you may ask? According to Peter Senge, author of The Fifth Discipline Fieldbook, “Systems thinking is a way of thinking about, and a language for describing and understanding, the forces and interrelationships that shape the behavior of systems”. Some systems are very complex, but all systems can be simplified to help understand the relationships between systems components. Systems can be "modeled" to help investigate their dynamics. We do not expect you to become system modelers, per se, but simple models can begin to help you understand how changes in one parameter might influence changes in another. Let's consider a simple system in which we have a bathtub, fed by a faucet, and drained at its lower level. We could diagram this simple system as follows…
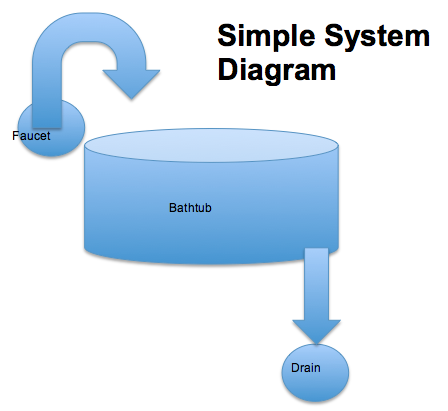
In this system there is a reservoir (the bathtub), an input (the faucet), and an output (the drain). The relationships in this system are simple and, hopefully, intuitive. If you want to run water into the tub for a long time to keep it quite warm, but not have it run over, what are your choices? You could keep the drain closed and run a very slow trickle of warm water into the tub from the faucet, letting it fill gradually, or, you could fill the tub quickly to some level, then open the drain to allow water to leave the tub at the same rate as it is being added to prevent further rise in the water level. Cold water is more dense than warm, so perhaps cooler water would drain preferentially and this would keep the tub water warmer overall. You could also evaluate the time it would take to fill the tub, or drain it, knowing the tub volume (gallons), the maximum input rate through the faucet (gallons/minute), and the maximum drain rate (gallons/minute).
Learning Checkpoint
Let's try a couple of simple model calculations to get you thinking about systems dynamics. First, we should establish some volumes and rates for this simple system. The tub (reservoir) will hold 30 gallons of water. The input and output values are outlined below:
1) If the faucet (input) will supply 3 gallons of water per minute, and the drain is closed (no output), how long will it take to fill the tub to the brim with water if the tub is empty to begin with?
ANSWER: The tub will fill in 10 minutes (30 gallon capacity divided by 3 gallons per minute input).
2) If the faucet supplies 3 gallons per minute, the tub is empty to begin with, but the drain allows 3 gallons per minute to leave the tub, how long will it take the tub to fill?
ANSWER: The tub will never fill because it starts empty and input = output!
3) If the faucet supplies 3 gallons per minute, the tub is empty to begin with, and the drain allows 1 gallon per minute to escape, how long will it take to fill the tub?
ANSWER: The tub will fill in 15 minutes (30 gallons capacity divided by (3 gallon/minute input minus 1 gallon per minute output).