Large earthquakes trigger seismicity dynamically from shaking as well as statically, from changing the surrounding stress field. Aftershocks are a specific class of triggered seismicity whose spatial and temporal properties have been well characterized by many empirical observations. By "empirical" I mean that the laws that govern the timing and size of aftershocks are not based on any kind of physics; instead they are merely fits to many observations. However, the observations have been so numerous that we know these fits are robust, hence we call them "laws." I hesitate to use the word "prediction" when talking of earthquakes, but in the case of aftershocks, their timing and areal extent can be estimated fairly accurately just from knowing the size and location of the mainshock.
Båth's Law
This empirical law states that the largest magnitude aftershock will be between 1.1 and 1.2 magnitude units smaller than the mainshock. This observation is independent of the size of the mainshock. Now is a good time to digress and mention that some of this categorization is definition dependent. What I mean is that, because of the way we define them, aftershocks can never be bigger than the mainshock. If an aftershock bigger than the mainshock were to occur, we'd just reclassify that one as the mainshock and call the previous biggie a foreshock. This may seem conveniently circular, but, logically, there's no other way to do it. The biggest earthquake in a sequence has to be called the mainshock.
Omori's Law
The Japanese seismologist after whom this law is named formulated his empirical observation about the temporal decay of aftershocks in the 1890s. (See Lesson 2 for more about his life and times!) He realized that the rate of aftershocks decays with time after the mainshock and that this decay happens to be inversely proportional to the time after the main shock. The modified version of his law is written like this:
N(t) ∝ (c+t)-p
in which N is the number of aftershocks as a function of time t after the mainshock and c and p are constants. In practice c is a very small number and p is somewhere around 1. In the case of c = 0 and p = 1, the equation above just simplifies to Omori's original law:
N(t) ∝ 1/t.

Try plugging in some numbers to this equation with any units you want for time, such as days. You will see that the number of aftershocks drops off rapidly at first and then decays more slowly. Once the number of aftershocks has dwindled to whatever the normal background seismicity rate is for the region, we say the aftershock sequence is over. Having trouble picturing this concept? See my screencast explanation of Omori's Law. Click here for a close-captioned explanation of Omori's Law.
People often get confused and think that this law governs both the size and timing of aftershocks. In fact, Omori's law says nothing about the size of aftershocks. The often-observed fact that bigger aftershocks usually happen pretty soon after the main shock is just a mathematical coincidence. Because there are fewer and fewer aftershocks at all as time gets farther from the main shock, the likelihood of one of them being big is also less. This is simply because there are always many more small earthquakes than big ones in any region for any period of time. (If you took EARTH 501, you will remember this from the frequency-magnitude plots you made in the New Madrid lesson.)
Rupture Area
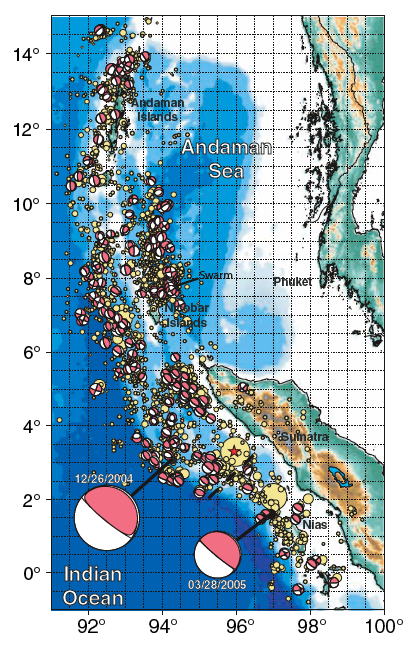
A third useful observation about aftershocks is that they usually cluster around the edges of the area ruptured by the main shock. I think this makes intuitive sense. You can think of an earthquake rupture as getting rid of all the built-up stress over the patch that breaks. However, maybe some of the excess stress at the edges where the earthquake stops is still there. As the fault gets used to the new stress field, little earthquakes happen at the boundary between what broke and what didn't. This feature of aftershocks comes in handy because it helps for estimating hazard and risk associated with aftershocks if you know approximately where they are going to be. It is also useful scientifically because it provides a check on the calculated size of the rupture area that seismologists normally derive from theoretical models. The map below shows aftershock locations following the 26 December 2004 Sumatra-Andaman earthquake. This earthquake ruptured the longest segment of a fault ever recorded, somewhere between 1300 and 1600 kilometers. You can see what a huge areal extent the aftershocks cover. Each little colored circle on the map below is an aftershock.