Lesson 5: Translating the coordinate system
New syntax introduced: translate(), pushMatrix(), popMatrix()
You know that the default coordinate system has (0,0) in the upper left corner and increases to the right and downwards. You can change this system by calling the function translate(). The translate() function takes two arguments: the number of pixels added to x and the number of pixels added to y. All shapes drawn after translate() will adhere to the new coordinate structure.
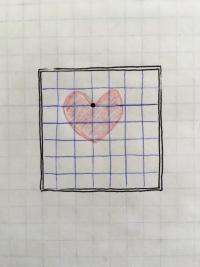
The tricky thing to remember about translation is that you aren't really moving the shapes you draw. Instead you are moving the entire coordinate system relative to the display window. Consider the hand-drawn sketch below in which there is a heart whose top cusp is at (3,2), shown by the black dot.
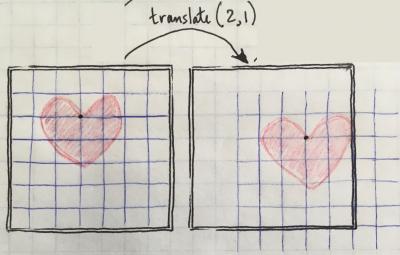
Now if I translate the coordinate system 2 over and 1 down, the display window stays where it is and the heart stays where it is relative to the coordinate mesh, but the coordinate mesh itself has been shifted. So in pseudo-code this would be like:
translate(2,1); heart(3,2);
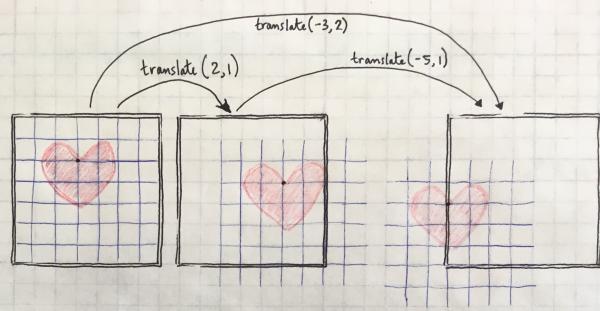
Translations are cumulative, so the third panel can be achieved either by translating (-5,1) from the second panel, or by translating (-3,2) directly from the first panel. If we had really drawn the third version in Processing, you'd only see the right half of the heart because the other side is out of the display window. Philosophers can tell us whether it exists or not, but in any case we can't see it.
So in pseudo-code this would be:
translate(2,1); translate(-5,1); heart(3,2);
Or it could have been
translate(-3,2); heart(3,2);
Note how I'm always drawing the heart itself with the same coordinates it had in the first place.
Example 5.6
Here is an example in an actual program. Notice in this program that rectangle is always specified by the same coordinates. You can see how translation is cumulative and can be negative, too.
// Demonstrate Translation size(200, 200); rect(10, 10, 50, 20); // Draw a rectangle translate(100, 100); // Move the origin to (100, 100) rect(10, 10, 50, 20); // Draw the same rectangle, but now it is shifted translate(50, 50); // Move the origin to (150, 150) rect(10, 10, 50, 20); // Same rectangle shifted more translate(0, -75); // Translations can be negative fill(255, 0, 0); rect(10, 10, 50, 20); // Same rectangle shifted up and colored red

To change the coordinate system temporarily and then have it go back to the way it was before you made a transformation without having to manually make a negative translation, use pushMatrix() and popMatrix(). These functions always have to be used together. The way it works is that you stick in a pushMatrix() before you write the transformation and then you stick in a popMatrix() just before you want to revert back. The coordinate system will revert back to the way it was before pushMatrix().
Example 5.7
// Use pushMatrix and popMatrix to revert the translation
size(200, 200);
pushMatrix();
for (int i = 1; i < 200; i++) {
translate(i, i);
rect(1, 1, 50, 20); // Draw a rectangle
}
popMatrix();
ellipse(100, 100, 20, 20);

Note how in the code in Example 5.7 the circle draws in the center of the screen because the for loop was enclosed by a pushMatrix() popMatrix() pair, meaning that all those accumulated translations didn’t affect the circle.
Quiz Yourself!
Exercises
5.5: Experiment with translations. See what happens when you make multiple translations and use more than one pushMatrix() popMatrix() pair