Market Equilibrium Example

Example: In a hypothetical market

Demand is given by: $P=100-2Q_d$
Supply is given by: $P=10+Q_s$

1. What is the competitive market equilibrium, the consumer surplus and the producer surplus?
2. Given the data from Question 1, how much wealth will a consumer make if his willingness to pay is 70? 40? 30?
3. Given the data from Question 1, how much wealth will a producer make if his willingness to accept is 70? 40? 30?

Part 1)

At equilibrium, supply equals demand (both quantity and price). So, first, we need to equate the supply and demand functions and find the equilibrium price and quantity $(Q*,P*)$ .

$P=100-2Q_d$
$P=10+Q_s$

Then,

$100-2Q_d=10+Q_s$

At equilibrium

$Q_d=Q_s$

$100-10=Q+2Q$

$90=3Q$

Then, equilibrium quantity will be $Q*=\frac{90}{3}=30$

By plugging equilibrium quantity ($Q*$ ) in one of the supply or demand equations (doesn’t matter which one, we should get the same answer), we will find the equilibrium price ($P*$ ):

$P_d=100-2Q_d$

$P*=100-2\left(30\right)=40$

The next step will be calculating the CS and PS at market equilibrium $(Q*,P*)$ :

$CS=\frac{\left(100-40\right)\left(30-0\right)}{2}=900$

$PS=\frac{\left(40-10\right)\left(30-0\right)}{2}=450$

And total wealth created by the market

$\text{Total Wealth}=CS+PS=900+450=1350$

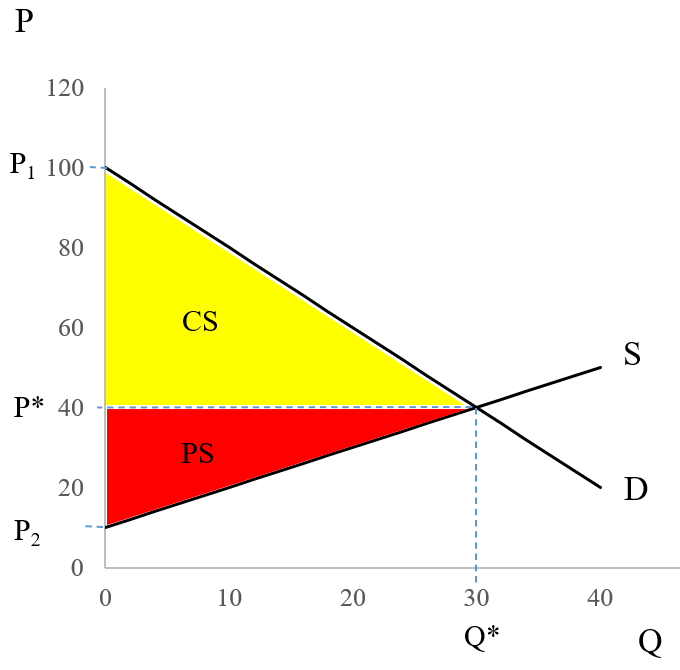
Note for review: Here are the steps in calculating the equlibrium, consumer surplus, and producer surplus:

• P* and Q* can be calculated by solving the supply and demand system of equations for P and Q, which give P* = 40 and Q* = 30
• Consumer surplus is the area of triangle above the P* and below the demand curve (yellow triangle): area = base times height/2
  • base of this triangle = Q* = 30
  • height = P₁ - P*
    P₁ is the intercept of demand function. So, we can find P₁ by plugging Q = 0 into the demand function.
    P₁ = 100 - 2*0 = 100
    Then, height = 100 - 40 = 60
  • Consumer Surplus = area of yellow triangle = base * height/2 = (30 * 60)/2 = 900
• Producer surplus, is the area of triangle below the P* and above the supply curve (red triangle): area = base times height/2
  • base of the red triangle = Q* = 30
  • height of the red triangle = P* - P₂
  • P₂ is the intercept of the supply curve. So, we just need to plug Q = 0 into the supply function to find the P₂.
    P₂ = 10 + 1*0 = 10
    So, height of the red triangle = P* - P2 = 40 - 10 = 30
  • Producer Surplus = area of red triangle = base * height/2 = (30*30)/2 = 450

Part 2)

$\text{Maximum willingness to pay}=70$ : the consumer will make $70-40=30$

$\text{Maximum willingness to pay}=40$ : the consumer will make $40-40=0$

$\text{Maximum willingness to pay}=30$ : the consumer will not buy the good because willingness to pay > price

Part 3)

$\text{Minimum willingness to accept}=70$ : the producer will not sell the good because willingness to accept < price

$\text{Minimum willingness to accept}=40$ : the producer will make $40-40=0$

$\text{Minimum willingness to accept}=30$ : the producer will make $40-30=10$

Take Aways

After working through the material on this page and reading the associated textbook content, you should be able to confidently:

1. calculate the consumer surplus created by a single trade and by a market;
2. calculate the producer surplus created by a single trade and by a market;
3. calculate the total wealth created by a single trade and by a market;
4. understand why a buyer decides to enter the market (or not);
5. understand why a seller decides to enter the market (or not);
6. understand why there are no trades to the right of the equilibrium.