Lesson 1: Energy and Society
The links below provide an outline of the material for this lesson. Be sure to carefully read through the entire lesson before returning to Canvas to submit your assignments.
Introduction & Checklist
Welcome to Lesson 1!
It looks like we are ready to go for lesson 1: Energy and Society. This lesson is going to teach us about energy! What is energy, and with which units do we measure energy? We will learn about the commonly used units we use to measure energy. There are different forms of energy that we use; for example, we use electrical energy or mechanical energy, like moving a car, etc., and we need to know the units in which we measure these different forms of energy. So we will also learn about forms of energy. We will learn about the units in which we measure these forms of energy, and also we will get into a very, very important distinction between energy and power. To be clear, that is the key concept in this lesson that I want you to concentrate on – power and energy. And once we know the difference, we know that using power, we can calculate energy, or if we know the energy and time, we can calculate power.
We will also look at some of those calculations. Once we know the power, we can calculate the energy. For example, a computer consumes some power, the rate at which energy is drawn, and if we use the computer for so many hours, what is the energy consumption by this computer? We can do the same thing for a refrigerator, or we can do it for any other appliance that you use at home. These are common appliances that we are using every day in our lives. When we add up the energy consumed by a computer, by a toaster, by an oven, by a refrigerator, by lighting, etc., at your place then you get energy consumption of all your equipment for a day. So we are going to do that and calculate energy consumption for a day, and then for a month, and we can calculate also the electric bill for one whole month -- that would be our objective in this lesson.
Be careful, again, because the distinction between energy and power is a very important concept. Forms of energy and the units in which we measure energy are the concepts that we will be looking at in this wonderful lesson. All Right! Why Wait? Let’s go and start our lesson.
Good Luck!
What is Energy?
When thinking about energy the following questions may come to mind:
- What is energy?
- How do we measure it?
- Where is it coming from?
- Do we have enough?
- What is the impact of energy use?
Energy is the lifeblood of any modern society. Energy is used in every walk of life. Without it, modern life would almost come to a standstill. From the moment of waking up in the morning with an alarm clock, we use energy for almost everything we do.
Energy is a property of matter that can be converted to work, heat, or radiation. It can move things or do work, produce heat even if it does not move anything, and be converted to light (or more accurately, radiation).
Lesson 1 Objectives
Upon completing this lesson, you should be able to:
- define energy
- articulate fundamental forms of energy
- know the different units of energy
- define and distinguish differences between energy and power
- classify Energy Sources
Checklist for Lesson 1
| Step | Activity | Access / Directions |
|---|---|---|
| 1 | Read the online lesson | Lesson 1 - Energy Supply and Demand |
| 2 | Review | Lesson 1 - Review & Extra Resources (supplemental materials that are optional...but informative!) |
| 3 | Take | Lesson 1 - Quiz (graded) The quiz is available in Canvas. |
Please refer to the Calendar in Canvas for specific timeframes and due dates.
Questions?
If you have any questions, please post them to the General Course Questions forum in located in the Discussions tab in Canvas. I will check that discussion forum daily to respond. While you are visiting the discussion board, feel free to post your own responses to questions posted by others - this way, you might help a classmate!
Forms of Energy, page 1 of 2
Six Basic Forms of Energy
Energy exists in a number of different forms, all of which measure the ability of an object or system to do work on another object or system. There are six different basic forms in which we use energy in our day-to-day life:
Mechanical Energy (Kinetic)
- Energy that a body possesses by virtue of its motion. A few examples are a baseball player pitching a ball, a plow being pulled by a tractor, and a hammer that is being used to pound nails.
- In the United States, we use about a third of our total energy for transportation or movement of people and goods.
Mechanical Energy (Potential)
- Energy that a body possesses by virtue of its position relative to a reference point. A few examples of mechanical energy include a pendulum, a bow (archery), a spring, and a hammer that is raised in preparation to pound nails.
Let's investigate further...
A book sitting on a shelf in the library is said to have potential energy because if it is nudged off the shelf, gravity will accelerate the book, giving the book kinetic energy. Because the Earth's gravity is necessary to create this kinetic energy, and because this gravity depends on the Earth being present, we say that the Earth-book system is what really possesses this potential energy, and that this energy is converted into kinetic energy as the book falls.
Chemical Energy
- Energy locked in the bonds of molecules in the form of microscopic potential energy, which exists because of the electric and magnetic forces of attraction exerted between the different parts of each molecule.
- It is the same attractive force involved in thermal vibrations.
- The molecular parts get rearranged in the chemical reactions, releasing or adding to this potential energy.
- Some examples include a battery, burning wood, and glucose in the body.
- As of 2020, approximately 80% of the energy used in the U.S. comes from fossil fuels such as coal, oil, and natural gas.
- All of these fuels store energy in the form of chemical energy.
- When they are burned, these fuels release energy in the form of heat or thermal energy.

The glucose (blood sugar) in your body is said to have "chemical energy" because the glucose releases energy when chemically reacted (combusted) with oxygen. Your muscles use this energy to generate mechanical force (work) and also heat.
Thermal or Heat Energy:
- Energy that combines microscopic, kinetic, and potential energy of the molecules. Some examples of this include a hot beverage and boiling water.
- Temperature is really a measure of how much thermal energy something has: The higher the temperature, the faster the molecules are moving around and/or vibrating, i.e., the more kinetic and potential energy the molecules have.
- Fuels (chemical energy) are oftentimes burned and converted to thermal or heat energy, which is then converted to motion in an automobile or electricity.
Thermal Energy
A hot cup of coffee is said to possess "thermal energy," or "heat energy," because it has a combination of kinetic energy (its molecules are moving and vibrating) and potential energy (the molecules have a mutual attraction for one another) - much the same way that the book on the bookshelf and the Earth have potential energy because they attract each other.
Forms of Energy, page 2 of 2
Electrical Energy:
- Energy created through the movement of electrons among the atoms of matter.
- Although electricity is seldom used directly, it is one of the most useful and versatile forms of energy. Following are some examples. When electricity is:
- put into a toaster, it can be converted to heat;
- put into a stereo, it is converted into sound;
- put into an electric bulb, it converts into light;
- put into a motor, it converts into motion or movement (mechanical energy).
- Due to its versatility, electricity is in high demand; in the US, about 40% of the total primary energy used is converted into electricity for various uses.
Remember This!
All matter is made up of atoms, and atoms are made up of smaller particles called protons (which have positive charge), neutrons (which have neutral charge), and electrons (which are negatively charged).
- The electrons orbit around the nucleus (which contains protons and neutrons), just like the planets orbit the sun.
- Certain metals have electrons that are only loosely attached to their atoms, so they can be easily made to move from one atom to another if an electric field is applied to them.
- When those electrons move among the atoms of matter, a current of electricity is created.
Nuclear Energy:
- Energy produced when reactions occur in an atom, resulting in some type of structural change in the nuclei.
- Fusion occurs when two small nuclei join together to create one large nucleus or particle, and during this process, energy is released in the form of light and heat. An example is in the Sun: hydrogen nuclei fuse (combine) together to make helium nuclei, which release energy.
- Fission occurs when the nucleus of one big atom splits into two new atoms, and during this process, a tremendous amount of energy is released in the form of light and heat. An example is in a nuclear reactor or the interior of the earth: uranium nuclei split apart, causing energy to be released.
Did You Know?
In both fusion and fission, some of the matter making up the nuclei is converted into energy, represented by the famous equation:
- This formula indicates that energy intrinsically stored in matter at rest equals its mass times the speed of light squared. When matter is destroyed, the energy stored is released.
- This equation suggests that an incredibly huge amount of energy is released when a small amount of matter is converted to energy.
Radiation:
- Energy radiated or transmitted in the form of rays, waves, or particles. Some examples include:
- visible light that can be seen by naked eye;
- infrared radiation;
- ultraviolet radiation (UV) that cannot be seen with the naked eye;
- long wave radiation, such as TV waves and radio waves;
- very short waves, such as x-rays and gamma rays.
Even things that we encounter in our every day life contain some radioactive material, either natural or man-made. Smoke detectors, compact fluorescent bulbs, some watches and granite countertops can emit some nuclear radiation. Even plane travel at high altitudes cause exposure from cosmic rays.
- Electromagnetic Radiation
- Energy from the sun comes to the earth in the form of Electromagnetic radiation, which is a type of energy that oscillates (side to side) and is coupled with electric and magnetic fields that travel freely through space.
- Electromagnetic radiation is composed of photons or particles of light, which are sometimes referred to as packets of energy.
- Photons, like all particles, have properties of waves.
Photons make the world a brighter place!
Photons are created when electrons jump to lower energy levels in atoms, and are absorbed when electrons jump to higher levels. Photons are also created when a charged particle, such as an electron or proton, is accelerated. An example of this phenomenon is a radio transmitter antenna that generates radio waves.
- Electromagnetic Spectrum
- The “Electromagnetic spectrum“ is a representation of the wide range of wavelengths of electromagnetic radiation.
- Photons are associated with visible light, which accounts for only a very limited part of the electromagnetic spectrum.
- A great discovery of the nineteenth century was that radio waves, x-rays, and gamma-rays are just forms of light, and that light is electromagnetic waves.
Please watch the following 5:00 video about the electromagnetic spectrum:
Something surrounds you. Bombards you. Some of which you can't see, touch, or even feel. Every day, everywhere you go. It is odorless and tasteless. Yet you use it and depend on it every hour of every day. Without it the world you know could not exist. What is it? Electromagnetic radiation. These waves spread across the spectrum from very short gamma rays to x-rays, ultraviolet rays, visible light rays, even longer infrared light waves, microwaves, to radio waves which can measure longer than a mountain range. This spectrum is the foundation of the information age and of our modern world. Your radio, remote control, text message, television, microwave oven, even a doctor's x-ray, all depend on waves within the electromagnetic spectrum.
Electromagnetic waves, or EM waves, are similar to ocean waves in that both are energy waves. They transmit energy. EM waves are produced by the vibration of charged particles and have electrical and magnetic properties. But unlike ocean waves that require water, EM waves travel through the vacuum of space at the constant speed of light. EM waves have crests and troughs like ocean waves. The distance between crests is the wavelength. While some EM wavelengths are very long and are measured in meters, many are tiny and are measured in billionths of a meter, nanometers. The number of these crests that pass a given point within one second is described as the frequency of the wave. One wave or cycle per second is called a Hertz. Long EM waves, such as radio waves, have the lowest frequency and carry less energy. Adding energy increases the frequency of the wave and makes the wavelength shorter. Gamma rays are the shortest, highest energy waves in the spectrum. So, as you sit watching TV, not only are there visible light waves from the TV striking your eyes, but also radio waves transmitting from a nearby station; and microwaves carrying cellphone calls and text messages; and waves from your neighbors Wi-Fi and GPS units in the cars driving by. There's a chaos of waves from all across the spectrum passing through your room right now.
With all of these waves around you, how can you possibly watch your TV show. Similar to tuning a radio to a specific radio station, our eyes are tuned to a specific region of the EM spectrum and can detect energy with wavelengths from 400 to 700 nanometers. The visible light region of the spectrum. Objects appear to have color because EM waves interact with their molecules. Some wavelengths in the visible spectrum are reflected and other wavelengths are absorbed. This leaf looks green because EM waves interact with the chlorophyl molecules. Waves between 492 and 577 nanometers in length are reflected and our eye interprets this as the leaf being green. Our eyes see the leaf as green but cannot tell us anything about how the leaf reflects ultraviolet, microwave, or infrared waves.
To learn more about the world around us, scientists and engineers have devised ways to enable us to see beyond that sliver of the EM spectrum called visible light. Data from multiple wavelengths help scientists study all kinds of amazing phenomena on Earth from seasonal change to specific habitats. Everything around us emits, reflects, and absorbs EM radiation differently based on it's composition. A graph across the EM spectrum is called the spectral signature. Characteristic patterns like fingerprints within the spectra allow scientists to determine an object's chemical composition and to determine such physical properties as temperature and density.
NASA's Spitzer space telescope observed the presence of water and organic molecules in a galaxy 3.2 billion light years away. Viewing our sun in multiple wavelengths with the SOHO satellite allows scientists to study and understand sunspots that are associated with solar flares and eruptions that are harmful to satellites, astronauts and communications here on Earth.
We are constantly learning more about our world and universe by taking advantage of the unique information contained in the different waves across the EM spectrum.
As depicted in the image above, the lower the energy, the longer the wavelength and lower the frequency, and vice versa.
The reason that sunlight can hurt your skin or your eyes is because it contains "ultraviolet light," which consists of high energy photons. These photons have short wavelength and high frequency, and pack enough energy in each photon to cause physical damage to your skin if they get past the outer layer of skin or the lens in your eye.
Radio waves, and the radiant heat you feel at a distance from a campfire, for example, are also forms of electromagnetic radiation, or light, except that they consist of low energy photons (long wavelength and high frequencies - in the infrared band and lower) that your eyes can't perceive. This was a great discovery of the nineteenth century - that radio waves, x-rays, and gamma-rays are just forms of light, and that light is electromagnetic waves.
About 20% of the electricity used in the US is used to produce visible light for lighting purposes.
Activity: Identifying Forms of Energy
Can you identify the different forms of energy in the picture below? Enter your answer in the table below and click the "Check Answers" button to check your work.
Click link to expand for a text description of the figure
These things, listed below, represent the six fundamental forms of energy: Mechanical, Chemical, Thermal/Heat, Electrical, Nuclear and Radiation. Your task is to determine what form of energy is represented by each item.
- Light bulb in a lamp post powered by?
- Two women sitting at a picnic table drinking water. The arrow is pointing to the cups of water. One cup is sitting on the table and the other is in a woman's hand.
- A doctor looking at an X-ray produced with?
- A Frisbee flying through the air powered by?
- The sun power by?
- A man getting ready to hit a golf ball with a golf club. The arrow is pointing at the head of the golf club which is powered by?
- A little boy eating an ice cream cone. The arrow is pointing to the ice cream that provided what to the child?
Now spend some time trying to identify the different forms of energy that are at work in the above items. Once you have thought through this and have some answers, read on to see if you are correct.
AnswersLight bulb in a lamp post - Electrical Energy
Cups of water. One is sitting on a table and the other is in a woman's hand. - Thermal or Heat Energy
An X-ray - Nuclear Energy
A Frisbee flying through the air - Mechanical (kinetic) Energy
The sun - Radiation
A golf club getting ready to hit a ball - Mechanical (Potential)
The ice cream in an ice cream cone - Chemical
Energy Conversion
Energy can be converted from one form to another.
Examples:
- Gasoline (chemical) is put into our cars, and with the help of electrical energy from a battery, provides mechanical (kinetic) energy.
- Purchased electricity is fed into our TVs and is converted to light and sound.
- Similarly, purchased electricity goes into an electric bulb and is converted to visible light and heat energy.
- The image below shows examples of more conversions.
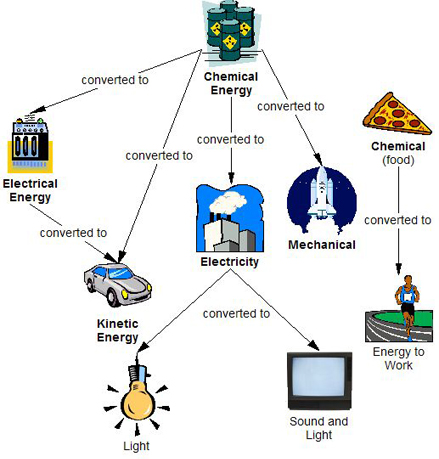
Click link to expand for a text description of figure
Chemical Energy is converted to Electrical Energy (stove), Kinetic Energy (car), Electricity (power plant), and Mechanical Energy (space shuttle). Electrical Energy is converted to Kinetic Energy. Electricity is converted to Light (light bulb) and Sound and Light (TV). Chemical food energy is converted to Energy to Work (person running).
Activity: Day-to-Day Conversion Devices
Activity: Day to Day Conversion Devices
Most of the day-to-day devices that we use are energy conversion devices. In this activity, you will identify the fundamental form of energy that is put in to each device and the output form of energy that is a result.
Your task is to look at six devices and decide what form of energy is the input and which is the output form of energy. Think about your answers carefully before reading ahead to the answers.
- Lawn Mower input form of energy? Output form of energy?
- Computer input form of energy? Output form of energy?
- Sun input form of energy? Output form of energy?
- Tree input form of energy? Output form of energy?
- Gas Furnace input form of energy? Output form of energy?
- Hair Dryer input form of energy? Output form of energy?
| Device | Input form of Energy | Output form of energy | |
|---|---|---|---|
| 1 | Lawn Mower | Chemical | Mechanical or kinetic |
| 2 | Computer | Electrical | Light and Sound |
| 3 | Sun | Nuclear | Radiant |
| 4 | Tree | Radiant | Chemical |
| 5 | Gas Furnace | Chemical | Thermal or Heat |
| 6 | Hair Dryer | Electrical | Heat or Electric |
Measurement of Energy
Units of Measurement
How is energy measured? It is measured in various units by various industries or countries, in much the same way as the value of goods is expressed in Dollars in the U.S. and Yen in Japan and Pounds in Britain.
The table below identifies different units for measuring energy. A lot of it also has some historical context. Our early studies of energy involved heating things up, so we name units based on how hard it was to heat things. Makes sense, right? Now we pass electrical energy to operate many devices, so now we use units that "better" capture this process.
| Unit | Definition | Used In | Equivalent to |
|---|---|---|---|
| British Thermal Unit BTU | A unit of energy equal to the amount of energy needed to raise the temperature of one pound of water by one degree Fahrenheit. Equivalent to energy found in the tip of a match stick. | Heating and Cooling industries | 1 BTU = 1,055 Joules (J) |
| calorie or small calorie (cal) | The amount of energy needed to raise the temperature of one gram of water by one degree Celsius. | Science and Engineering | 1 calorie = 0.003969 BTUs |
| Food Calorie, Kilocalorie or large calorie (Cal, kcal, Calorie) | The amount of energy needed to raise the temperature of one kilogram of water one degree Celsius. The food calorie is often used when measuring the energy content of food. | Nutrition | 1 Cal = 1,000 cal, 4,187 J or 3.969 BTUs |
| Joule (J) | It is a smaller quantity of energy than calorie and much smaller than a BTU. | Science and Engineering | 1 Joule = 0.2388 calories and 0.0009481 BTUs |
| Kilowatt Hour (kWh) | An amount of energy from the steady production or consumption of one kilowatt of power for a period of one hour. | Electrical fields | 1 kWh = 3,413 BTUs or 3,600,000 J |
| Therm | A unit describing the energy contained in natural gas. | Home heating appliances | 1 therm = 100,000 BTUs |
Did You Know?
When writing BTUs, one uses a base of “10” raised to a particular exponent.
For example:
More specific notation involves the following:
To express measurements greater than those with a base of 10, you would do the following:
Here is a fun way to understand your energy use
Prof. Bruce Logan [1] of Penn State published a fascinating way to view your energy and climate impact. Using what you learned in this section, you can start to piece together just how much energy each of us uses to maintain our busy lifestyles.
The premise of this approach is to define (another!) unit of energy, but one with a bit more meaning. The daily energy unit, D. We are all supposed to eat about 2000 food Calories a day to survive. So, let’s set this amount of energy to equal 1 D. Now, how many Ds does the typical U.S. home each day (normally in KWh) or operate a car (normally joules or BTUs )? This method of comparing energy consumption allows us to better understand the scale of our energy habits (which might be shocking!) and tell you how many big mac-powered humans it would take to do what your car does…
Here are a few examples he shows to give you an idea.
- Food for 1 day = 1 D
- Running a single 100 W light bulb all day = 1.03 D
- Average daily electricity use for a US house = 13 D
- 1 gallon of gasoline used in an average car (goes 18 miles) = 15.2 D
- Natural gas for daily heating a US house = 31 D
Once we tally up all the energy it takes to fuel our lifestyle (professional + personal uses), each person consumed about 101 D of energy! (remember this is daily) For comparison, a Swiss citizen consumes about 54 D. Check out his website for more comparisons [1]. Watch this video (5 min 46 sec)
Energy Literacy The daily energy unit "D"
By Bruce Logan Penn State University.
If we want to communicate we need to speak the same language. How can we do that, well we translate it into something we know, into one common language. If you want to communicate when it comes to energy, how do we do that. We translate it into something that we know. Something we all know is that we need about 2,000 calories a day to live. That's something we can relate to. But how do we relate that to other things that either consume energy or produce energy in our lives.
Well, for example, if I were to take that 2,000 calories a day that I eat and use that energy to power 100 watt light bulbs, how many could I power. 3 4 5 10? The answer is just one light bulb. A single light bulb running continuously consumes the equivalent of about 2,000 calories a day.
Now if you look at all the things that we encounter in our lives in terms of energy units, so many of them have different units. For example 2,000 calories with a capital C is really 2,000 kilocalories. Daily food for a horse is 20,000 kilocalories. The energy in a gallon of gasoline 114 thousand BTUs or British thermal units. Or maybe you look at the engine in your car and it's 120 horsepower.
How can we understand these units. Well, one way is we could put them all on the basis of a kilowatt hour. However, look at those numbers. They're all still rather confusing and it's tough to relate to a kilowatt hour. So we need to find something that's not quite so confusing.
I propose that we define 2,000 calories a day, or the food that one person eats, as the unit 1D. One daily energy unit. If we use that unit, we could say well, our home uses 13D. Or while we eat 1D, a horse needs to eat 10D. The energy in a gallon of gasoline is about 14D.
So this common unit of D, allows us to now compare all these things in terms of something that we know, that is how much food we need to stay alive. And that unit of 1D is the same to everybody on the planet. Some people need a little bit more some people need a little bit less, but the general concept of the food we eat every day can help define what energy consumption is like.
So when you look at things now, for example, you can see the electricity that we consume per capita, not necessarily just in your home, but averaged across to all people in the US, is about 40 D, and all energy normalized per person in the U.S. is about 104 D. That makes this unit of D very nice because it ranges for the food and other activities up to about a maximum of about a hundred.
Look at your car which say gets 18 miles per gallon and your commuting 18 miles. Your commute costs you about 14D, 1 gallon of gas. If you were to travel in a more fuel-efficient car, say a Toyota Prius or something like that, that commute might only take 4.9D because you would use less gasoline. Or what if you used an electric car. Well to charge that car and use the energy in that battery, it's about 27 kilowatt hours to go 100 miles or 2.1D.
Let's say that you want to put solar panels on your house. Well each solar panel produces 0.43D. That means averaged over the day and with typical sunlight, and for example Pennsylvania, you would achieve about 0.43 D of energy capture out of each one of those panels. So if your house uses 13D, well you need about 30 solar panels. If your car is an electric car and it uses 2.1 D, then your commute needs about 2.1D or about 5 or 6 solar panels.
How much energy should we use. Well there's a study done by ETH Zurich which suggests a 2,000 watt Society. 2,000 watts is about 20D. Currently, Switzerland has the average population having about 53 D which is about half of what we consume in the U.S., which is about 104D. So if we're gonna have to try and reduce our energy consumption that's gonna have to go down quite a lot.
Going forward, how can we do that. Well, can you reduce the energy for your commute. Can you save more energy at home or energy you say for transport or food or put a solar panels on your house and reduce your consumed D.
So the question really is, going forward, how can we make that 20D green.
Thanks for listening and I hope that you find a way to use D in your life to understand the energy you can see.
Sources of Energy
Energy is stored and is available in different forms and sources. The ~24,000 times more solar energy that is available than we need is not in a readily usable form. It needs to be concentrated.
For example, when oil (a concentrated fuel) is burned with air, the resulting gases can reach high temperatures. Solar energy, as it is, is not concentrated and cannot reach those high temperatures. Therefore, we use more concentrated energy sources. These sources are divided into two groups—renewable and nonrenewable.
Renewable Energy Sources:
- Energy sources that can be replenished over and over again; they are never depleted. Some examples include hydropower, solar, wind, tidal, geothermal energy from inside the earth, biomass from plants, and nuclear fusion.
- These types of energy sources are usually converted into electricity or thermal (heat) energy.
Nonrenewable Energy Sources:
- Energy sources that we are using up and cannot produce in a short period of time. Some examples include fossil fuels (Petroleum Oil, Natural Gas, and Coal), Tar Sands, and Nuclear Fission.
- Another nonrenewable energy source is the element uranium, whose atoms we split (through a process called nuclear fission) to create heat, and ultimately, electricity.
- These types of energy sources are usually converted into electricity and mechanical energy.
- We get most of our energy from these nonrenewable energy sources.
Did You Know?
They're called fossil fuels because they were formed over millions and millions of years by the action of heat from the Earth's core and pressure from rock and soil on the remains (or 'fossils') of dead plants and animals.
Fossil Fuel Distribution
Fossil fuels, non-renewable energy sources formed over a million years, are not distributed uniformly over the earth’s surface. Depending on the climate conditions millions of years ago, certain parts of the land masses were favorable for organic matter to grow and thrive.
Over geological ages, these land masses moved, and certain regions are richer in fossil fuels than others. Review the information on the map below, and then answer the questions below the map based on your observations.
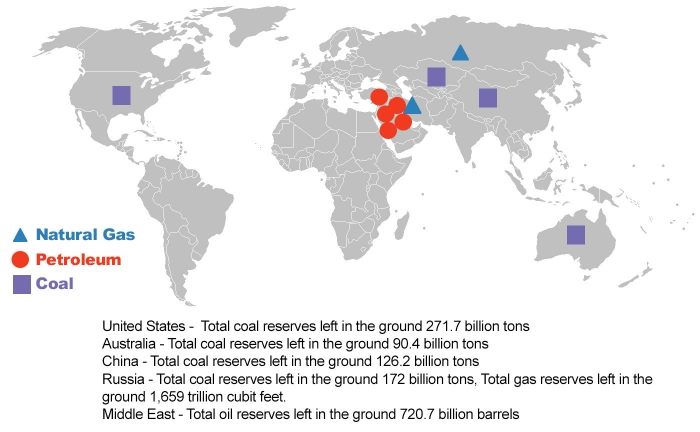
Click link to expand for a text description of the image
Global Distribution of Natural Resources
The most abundant resources for various global regions are as follows:
- China is richest in coal
- Australia is richest in coal
- The Middle East is richest in petroleum
- The United States is richest in coal
- Russia is richest in natural gas
Human Use of Energy Sources
The activity below is a drag and drop. Select the items listed in the center of the image and drag them to the corresponding or matching energy type listed on the side.
Click link to expand for a text description of Figure
Human use of Energy Sources
The following eight items are examples of how renewable and nonrenewable energy sources are used. Take some time to decide if each example is renewable or nonrenewable and then describe its specific source. (wind, sun, geothermal, water, oil, natural gas, uranium, or coal).
The answers will be at the bottom of the page.
- Nuclear power plant
- Gas stove
- Dam
- Gas pump
- Geothermal heat pump
- Power lines
- Solar panels
- Windmills
ANSWERS:
- Nuclear power plant is a nonrenewable energy source using uranium as its source.
- The gas stove is an example of nonrenewable energy source that uses natural gas as its source.
- A dam is an example of a renewable energy source that uses water as its source.
- A gas pump is an example of a nonrenewable energy source that uses petroleum as its source.
- A geothermal heat pump is a renewable energy source that uses geothermal heat (ground heat) as its source.
- Power lines are an example of a nonrenewable energy source that uses coal as its source.
- Solar panels are a renewable energy source that use the sun as their source.
- Windmills are a renewable energy source that use the wind as their source.
Power
What is Power?
Click the "play" button below and observe what happens. (Note: The video has no audio.)
Power vs. Energy
Both cyclists did the same amount of work (they both pedaled 10 miles), and used the same amount of energy (218 calories). The blue cyclist, however, demonstrated the most power, because he did the equivalent amount of work as the red cyclist, but in a faster time.
Power is the rate at which we do work.
Energy is the capacity to do work.
Work is the amount done.
Measuring Power
Units of Power are not the same as units of energy (i.e., Btus, calories). Units of power are measured in terms of units of energy used per some unit of time.
Examples of Units of Power include:
- Watt (W) = 1 joule of energy per second or 1 J/S
- BTU per hour (BTUs/h) = 1,055J
- Horsepower (hp) = 550 foot-pounds per second or 550 ft lb/S
- Calories per second (cal/sec)
- Kilowatt (kW) = 1,000 watts
Calculating Power
Power can be determined by the following formula:
Example
On a winter day, a home needs 1 x 106 or 1,000,000 BTUs of fuel energy every 24 hours to maintain the interior at 65° F. At what rate is the energy being consumed in Watts?
If 1 J/s = 1 Watt, and 1,000 Watt = 1kW, then 12,200 J/s = 12,200 Watts = 12.2 kW
 To solve this problem, you must realize the following: You know the Power (1,000,000 BTUs/24 hours) and the time (24 hours), so you need to solve for Energy. The measurements must be consistent, so the BTUs should be converted to a consistent measure, such as Joules:
To solve this problem, you must realize the following: You know the Power (1,000,000 BTUs/24 hours) and the time (24 hours), so you need to solve for Energy. The measurements must be consistent, so the BTUs should be converted to a consistent measure, such as Joules:
If using Joules per second instead of watts, you must convert 24 hours into seconds or divide it by the number of seconds in an hour (3,600).
Image Credit: © Penn State University, is licensed under CC BY-NX-SA 4.0 [4]
Power & Cost of Energy
We can also use a version of the Power formula to determine Cost of Energy:
Example
If a 100 W light bulb is accidentally left on overnight (8 hours), how much energy does it consume?
How much energy does this cost, if electricity costs 10 cents per Kilowatt?
Energy Use of Home Appliances, page 1
Calculating Energy Use
How is energy use of Home Appliances calculated?
You just learned in a previous discussion on power that:
or
By modifying this formula slightly, we can determine Energy Consumption per Day:
Where:
- Energy Consumption will be measured in Kilowatt hours (kWh) - like on your utility bills.
- Power Consumption will be measured in Watts
- Hours used per Day will be the actual time you use the appliance.
Since we want to measure Energy Consumption in Kilowatt hours, we must change the way Power Consumption is measured from Watts to Kilowatts (kWh). We know that 1 kilowatt hour (kWh) = 1,000 Watts hours, so we can adjust the formula above to:
Example 1: Calculating Energy Use of a Ceiling Fan
If you use a ceiling fan (200 watts) for four hours per day, and for 120 days per year, what would be the annual energy consumption?
Use this formula:
Energy Consumption / Day (kWh) = Power Consumption ( Watts / 1000) × Hours Used / Day
Energy Consumption per Day (kWh) = (200 / 1000) × 4 (hours used per day)
Energy Consumption per Day (kWh) = (1/5) × 4
Energy Consumption per Day (kWh) =4/5 or 0.8
So the Energy Consumption per Day is 0.8 kWh To find out energy for 120 days, do simple multiplication: 0.8 x 120 = 96 kWh
Example 2: Calculating Annual Cost of a Ceiling Fan
If the price per kWh for electricity is $0.0845, what is the annual cost to operate the ceiling fan?
Want Another Example?
If you use a personal computer (120 Watts) and monitor (150 Watts) for four hours per day, and for 365 days per year, what would be the annual energy consumption?
So the Energy Consumption per Day is 1.08 kWh. To find out energy for 365 days, do simple multiplication:
The annual cost if electricity is $0.0845 per kWh would be:
Energy Use of Home Appliances, Page 2, Practice
What is the energy consumption of a refrigerator with a wattage rating of 700 Watts when it is operated for 24 hours a day?
Step 1
To solve, use the following formula:
Where:Energy Consumption = Watt Hours (Wh) or KiloWatt Hours (kWh)
Power Consumption = Watts (W) or kW (KiloWatts)
Number of Hours Operated = Hours (h) For the example above:
Energy Consumption = 700 W x 24 h
Energy Consumption = 16800 W h
Step 2
To convert from Wh to kWh, remember that 1kWh = 1000 Wh
To solve, set up as a ratio and use linear algebra to solve for ?.
Practice Problem
Use the following link to generate a random practice problem [5].
Energy Use of Home Appliances, Page 3
Locating Wattage
You can usually find the wattage of most appliances stamped on the bottom or back of the appliance, or on its "nameplate." The wattage listed is the maximum power drawn by the appliance. Since many appliances have a range of settings (for example, the volume on a radio), the actual amount of power consumed depends on the setting used at any one time.

A refrigerator, although turned "on" all the time, actually cycles on and off at a rate that depends on a number of factors. These factors include how well it is insulated, room temperature, freezer temperature, how often the door is opened, if the coils are clean, if it is defrosted regularly, and the condition of the door seals.
To get an approximate figure for the number of hours that a refrigerator actually operates at its maximum wattage, divide the total time the refrigerator is plugged in by three.
The table below shows wattage of some typical household appliances.
| Appliance | Wattage (range) |
|---|---|
| Clock Radio | 10 |
| Coffee Maker | 900 - 1200 |
| Clothes Washer | 350 - 500 |
| Clothes Dryer | 1800-5000 |
| Dishwasher | 1200-2400 |
| Hair Dryer | 1200-1875 |
| Microwave Oven | 750-1100 |
| Laptop | 50 |
| Refrigerator | 725 |
| 36" Television | 133 |
| Toaster | 800-1400 |
| Water Heater | 4500-5500 |
| Appliance | Wattage |
|---|---|
| Aquarium | 50 - 1210 |
| Clock Radio | 10 |
| Coffee Maker | 900 - 1200 |
| Clothes Washer | 350 - 500 |
| Clothes Dryer | 1800-5000 |
| Dishwasher | 1200 -2400 (using the drying feature greatly increases energy consumption) |
| Dehumidifier | 785 |
| Electric Blanket - Single/Double | 60 / 100 |
| Fan - ceiling | 65 - 175 |
| Fan - window | 55 - 250 |
| Fan - furnace | 750 |
| Fan - whole house | 240 - 750 |
| Hair Dryer | 1200 - 1875 |
| Heater (portable) | 750 - 1500 |
| Clothes Iron | 1000 - 1800 |
| Microwave Oven | 750 - 1100 |
| Personal Computer - CPU - awake / asleep | 120 / 30 or less |
| Personal Computer - Monitor - awake / asleep | 150 / 30 or less |
| Laptop | 50 |
| Radio (stereo) | 70 - 400 |
| Refrigerator (frost free, 16 cubic feet) | 725 |
| 19" Television | 65 - 110 |
| 27" Television | 113 |
| 36" Television | 133 |
| 53" - 61" Projection TV | 170 |
| Flat Screen TV | 120 |
| Toaster | 800-1400 |
| Toaster Oven | 1225 |
| VCR / DVD | 17 - 21 / 20 - 25 |
| Vacuum Cleaner | 1000 - 1440 |
| Water heater (40 gallon) | 4500 - 5500 |
| Water pump (deep well) | 250 - 1100 |
| Water bed (w/heater, no cover) | 120 - 380 |
Amperes and Voltage

If the wattage is not listed on the appliance, you can still estimate it by finding the current draw (in amperes) and multiplying that by the voltage used by the appliance.
Most appliances in the United States use 120 volts. Larger appliances, such as clothes dryers and electric cooktops, use 240 volts. The amperes might be stamped on the unit in place of the wattage.
If not, find an ammeter to measure the current flowing through it. You can obtain this type of ammeter in stores that sell electrical and electronic equipment.
Take a reading while the device is running; this is the actual amount of current being used at that instant.
Phantom Loads
Also note that many appliances continue to draw a small amount of power when they are switched "off."
These "phantom loads" occur in most appliances that use electricity, such as VCR, televisions, stereos, computers, and kitchen appliances.
Most phantom loads will increase the appliance's energy consumption a few watts per hour. These loads can be avoided by unplugging the appliance or using a power strip and using the switch on the power strip to cut all power to the appliance.
Review & Extra Resources
Review
Watch this 3 minute 41 second video review Lesson 1
Hello everyone. Dr hall here.
So what we have collected here is a review sheet to help you identify some of the key facts and pieces of information that we covered in the first lesson.
One of the most important things that we covered is that there are six forms of energy and I hope throughout this lesson you will understand each of these and what they represent and you can identify some examples.
Next it's important to note that the forms of energy can be converted from one to another right. So we can go from chemical energy to thermal energy and vice versa depending on the process we're using. Another important factor is that there are some key units that we use to understand energy and quantify and we will switch between a lot of these throughout the course. Some of these are BTUs calories with a capital C, calories with a lowercase c joules kilowatt hours and therms. So each of these are important and quite often used in different fields so you have to be comfortable with each of these because you'll likely see it many times many different circumstances.
So there are also units of power which is distinctly different from energy and that's important to understand and appreciate the difference. The units for power are watts, kilowatts, joules per second, horsepower, and calories per second.
We also touched on the sources of energy some of them are renewable and here we define renewables those that can be replenished over and over again and are not depleted. Some examples of those are hydropower solar wind tidal and geothermal energy. There are also non-renewable sources and the way we define these is that they cannot be replenished over and over again in a reasonable amount of time. Some of these include fossil fuels tar sands and nuclear fission. So they rely on finite sources that take a long time to form. And as a part of our sources of energy section we also covered fossil fuel distribution uh across the world and in the us so that you can understand where these finite resources are and how much we have.
So in covering all of these previous topics you'll also note that there are a few important definitions. Power is the rate at which we do work right so it's how much work we can get done in a given amount of time. Energy is our capacity to do work and work is the amount of things that we get done. And many of these are interrelatable so for example power is energy divided by some period of time. Energy is power multiplied by a duration of usage. And energy consumption per day is equal to power consumption times those hours used within a day.
So i think if you focus on each of these key concepts here and the fact sheet provided to you I think you'll find them easier and there will also be some practice questions in which these concepts will help okay. So please study this practice the practice questions frequently frequently and when you're ready please proceed to the quiz.
Okay, good luck everyone.
Review Sheet - Energy and Society
- Forms of Energy
- Mechanical energy
- Potential Energy
- Kinetic Energy
- Chemical Energy
- Thermal or Heat Energy
- Electrical Energy
- Nuclear Energy
- Fission
- Fusion
- Radiation
- Mechanical energy
- Electromagnetic Spectrum
- The lower the energy, the longer the wavelength and lower the frequency, and vice versa
- Energy can be converted from one form to another
- Units of Energy
- BTU, Calorie, calorie, Joules, kWh, Therm
- Food Calorie (usually written with 'C')
- calorie (usually written with 'c')
- 1 Food Calorie = 1000 calories
- Units of Power
- Watts
- kW (kilo-watts)
- J/s
- HP
- cal/s
- Sources of Energy
- Renewable
- Can be replenished over and over again; they are never depleted
- Hydropower, Solar, Wind, Tidal, Geothermal energy from inside the earth, Biomass from plants, Nuclear Fusion
- Non-renewable
- Cannot be replenished over and over again; they get depleted
- Fossil fuels, Tar Sands, Nuclear Fission
- Fossil Fuel Distribution
- US has a lot of Coal reserves
- Middle East has a lot of petroleum reserves
- Renewable
- Definitions
- Power is the rate at which we do work
- Energy is the capacity to do work
- Work is the amount done
- Power = Energy / Time
- Energy = Power x Duration of Usage (time)
- Energy consumption/day = Power consumption x hrs used/day
Extra Resources
For more information on topics discussed in Lesson 1, see these selected references:
Lesson 1 Deliverable
Deliverable
You must complete a short quiz that covers the reading material in lesson 1. The Lesson 1 Quiz can be found in the Lesson 1: Energy and Society module in Canvas. Please refer to the Calendar in Canvas for specific time frames and due dates.