Lesson 3: Energy Efficiency
The links below provide an outline of the material for this lesson. Be sure to carefully read through the entire lesson before returning to Canvas to submit your assignments.
Introduction
Welcome to Lesson 3!
Alright, we are into lesson 3. Lesson 3 basically deals with energy efficiency. Upon completing this lesson, you will really get a quantitative feel for what energy efficiency is and also how to calculate energy efficiency with a conversion device. A conversion device can be anything – an automobile or a power plant or any device that converts one form of energy to another form.
And we will also understand the concept of entropy. Entropy is disorder. Because of entropy, our efficiencies are lower than what we normally expect. And we will look at the operating principle of a heat engine. A heat engine is a device that converts heat to work. Particularly, automobiles are all heat engines, and they are notoriously inefficient. We will see 2 examples and calculations of why these automobiles are notoriously inefficient.
We can also calculate the efficiency of a whole process from the step efficiencies. For example, if it involves 2 or 3 steps like in a relay race. You know you have 3 or 4 players taking the baton and one lap by each of the athletes. So, what is the overall or team efficiency if we know the efficiency of each of those steps or the efficiency of each of those players? That is a very important concept in this chapter.
While doing this, we will also learn about temperature scales; Kelvin scale, Fahrenheit, and also Celsius. So there will be a lot of numerical problems in this lesson.
Alright! Good luck!
Lesson 3 Objectives
Upon completing this lesson, you should be able to:
- define and calculate efficiency of an energy conversion device;
- articulate the concept of entropy;
- explain operating principles of a heat engine; and
- calculate overall efficiency from step efficiencies.
See the calendar in Canvas for due dates/times.
Questions?
If you have any questions, please post them to the General Course Questions forum in located in the Discussions tab in Canvas. I will check that discussion forum daily to respond. While you are visiting the discussion board, feel free to post your own responses to questions posted by others - this way, you might help a classmate!
Energy Conversion Devices
In the first lesson, we saw that energy can be transformed from one form to another, and during this conversion, all the energy that we put into a device comes out. However, all the energy that we put in may not come out in the desired form.
For example, we put electrical energy into a bulb and the bulb produces light (which is the desired form of output from a bulb), but we also get heat from the bulb (undesired form of energy from an electric bulb).

Therefore, energy flow into and out of any energy conversion device can be summarized in the diagram below:
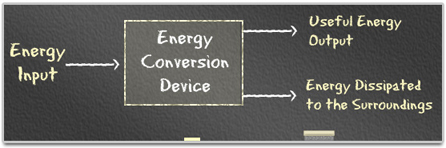
When all forms of energy coming out of an energy conversion device are added up, it will be equal to the energy that is put into a device. Energy output must be equal to the input. This means that energy can not be destroyed or created. It can only change its form.
In the case of an electric bulb, the electrical energy is converted to light and heat.
The amount of electrical energy put into a bulb = the amount of light energy (desirable form) plus the heat energy that comes out of the bulb (undesirable form).
 Say you go to the mall with $100, and you come back with only $10. You need to account for the $90 that was spent. After thinking about it, you come up with the following list:
Say you go to the mall with $100, and you come back with only $10. You need to account for the $90 that was spent. After thinking about it, you come up with the following list:
Gas ($15); Sandwich, fries, and a drink ($8); Lost ($5); New clothes ($62)
So you spent $62 on something useful - the clothes - but you spent additional money for other things that were necessary for your trip to the mall.
Self Check
Instructions: Identify the useful energy output(s) and undesirable energy output(s) in the energy conversion devices below. Enter your answers in the fields provided, and click the "Check" button to check your work.
Self Check:
Energy Conversion Devices
For each of the following examples, determine the types of useful energy and undesired energy for the given energy converter.
Example 1: Lawnmower with a chemical energy input. (Hint: How do you know when your neighbor is mowing the lawn?)
Example 2: Car with a chemical energy input. (Hint: Think about mufflers, tires, and generator.)
Example 3: Television with an electrical energy input. (Hint: Have you ever felt the back of your TV after it has been on for a few hours?)
Example 4: Desktop computer with an electrical energy input. (Hint: What’s in your tower and why?)
Answers:
Example 1: The useful energy for a lawnmower is mechanical, while the undesired energy is thermal (heat) and radiation (noise).
Example 2: The useful energy for a car is mechanical, while the undesired energy is thermal or heat (tail pipe).
Example 3: The useful energy for a TV is radiation (light and sound) and the undesirable energy is heat (from circuits).
Example 4: The useful energy for a computer is radiation (light and sound) and the undesirable energy is heat (circuits – electrons moving through system) and mechanical (fan for cooling).
Efficiency of Energy Conversion Devices
Efficiency is the useful output of energy. To calculate efficiency, the following formula can be used:
Example 1
An electric motor consumes 100 watts (a joule per second (J/s)) of power to obtain 90 watts of mechanical power. Determine its efficiency.
Solution:
Input to the electric motor is in the form of electrical energy, and the output is mechanical energy.
Using the efficiency equation:
Or efficiency is 90%.
Caution!
This is a simple example because both variables are measured in Watts. If the two variables were measured differently, you would need to convert them to equivalent forms before performing the calculation.
Practice Problem
Use the following link to generate a random practice problem [1] similar to the Practice 1 example.
The previous example about an electrical motor is very simple because both mechanical and electrical power is given in Watts. Units of both the input and the output have to match; if they do not, you must convert them to similar units.
Example 2
The United States' power plants consumed 39.5 quadrillion Btus of energy and produced 3.675 trillion kWh of electricity. What is the average efficiency of the power plants in the U.S.?
Solution:
Total Energy input = 39.5 x 10^15 Btus and the Useful energy output is 3.675 x 10^12 kWh. Recall that both units have to be the same. So we need to convert kWh into Btus. Given that 1 kWh = 3412 Btus:
Step 1
Therefore:
Step 2
Use the formula for efficiency.
Practice 2
The United States' power plants consumed 39.5 quadrillion Btus of energy and produced 3.675 trillion kWh of electricity. What is the average efficiency of the power plants in the U.S.?
Practice Problem
Use the following link to generate a random practice problem [2] similar to the Practice 2 example.
Energy Efficiencies
Energy efficiencies are not 100%, and sometimes they are pretty low. The table below shows typical efficiencies of some of the devices that are used in day to day life:
| Device | Efficiency |
|---|---|
| Electric Motor | 90 % |
| Home Gas Furnace | 95 % |
| Home Oil Furnace | 80 % |
| Home Coal Stove | 75 % |
| Steam Boiler in a Power Plant | 90 % |
| Overall Power Plant | 36 % |
| Automobile Engine | 25 % |
| Electric Bulb: Incandescent | less than 10 % |
| Electric Bulb: Fluorescent | 60 % |
| Electric Buld: LED | 90 % |
From our discussion on national and global energy usage patterns in Lesson 2, we have seen that:
- about 40% of the US energy is used in power generation;
- about 27% of the US energy is used for transportation.
Yet the energy efficiency of a power plant is about 35%, and the efficiency of automobiles is about 25%. Thus, over 62% of the total primary energy in the U.S. is used in relatively inefficient conversion processes.
Why are power plant and automobile design engineers allowing this? Can they do better?
There are some natural limitations when converting energy from heat to work.
Measuring Thermal Energy
Thermal energy is energy associated with random motion of molecules. It is indicated by temperature, which is the measure of the relative warmth or coolness of an object.
A temperature scale is determined by choosing two reference temperatures and dividing the temperature difference between these two points into a certain number of degrees.
The two reference temperatures used for most common scales are the melting point of ice and the boiling point of water.
- On the Celsius temperature scale, or centigrade scale, the melting point is taken as 0°C and the boiling point as 100°C, with the difference between them being equal to 100 degrees.
- On the Fahrenheit temperature scale, the melting point is taken as 32°F and the boiling point as 212°F, with the difference between them being equal to 180 degrees.
It is important to realize, however, that the temperature of a substance is not a measure of its heat content, but rather, the average kinetic energy of its molecules resulting from their motions.
Try This!
Below is a 6-ounce cup with hot water and a 12-ounce cup with hot water at the same temperature.
- Do they have the same heat content?
- Do they have the same amount of energy?
Instructions: Click the play button to obtain a magnified view of what is happening. Draw your conclusions, enter your answer in the text field provided, and then click the link below the video to check your answer. (Note: The animation has no audio.)
Try This: Measuring Thermal Energy
A six ounce cup and a twelve ounce cup are both filled with 85 degree water.
Conclusion: They do NOT have the same heat content. Since water in the two cups is at the same temperature, the average kinetic energy of the molecules in the cups is the same; however, the 12 ounce cup has twice as many molecules when compared with the 6 ounce cup and thus has the greater total motion or heat energy.
Kelvin Scale
When water molecules freeze at 0°C, the molecules still have some energy compared to ice at -50°C. In both cases, the molecules are not moving, so there is no heat energy.
So what is the temperature at which all the molecules have absolutely zero energy? A temperature scale can be defined theoretically, for which zero degree corresponds to zero average kinetic energy. Such a point is called absolute zero, and such a scale is known as an absolute temperature scale. At absolute zero, the molecules do not have any energy.
The Kelvin temperature scale is an absolute scale having degrees the same size as those of the Celsius temperature scale. Therefore, all the temperature measurements related to energy measurements must be made on Kelvin scale.
You can convert a temperature in Celsius (c) to Kelvin (k) with this formula:
You can also change a temperature in Kelvin to Celsius:
To make calculations for this class easier, you may round off and use just 273 in your conversions.
Try This!
Instructions: Click the "Play" button below and notice what happens to the ice cube. Answer the questions that follow based on your observations. (Note: The animation has no audio.)
Heat Engines
Energy conversions occurring in an automobile are illustrated below:
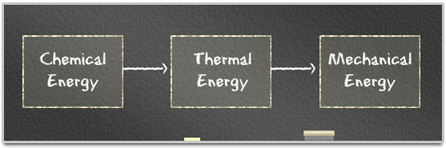
Any device that converts thermal energy into mechanical energy—such as an automobile or a power plant—is called a heat engine. In these devices, high temperature heat (thermal energy) produced by burning a fuel is partly converted to mechanical energy to do work and the rest is rejected into the atmosphere, typically as a low temperature exhaust.
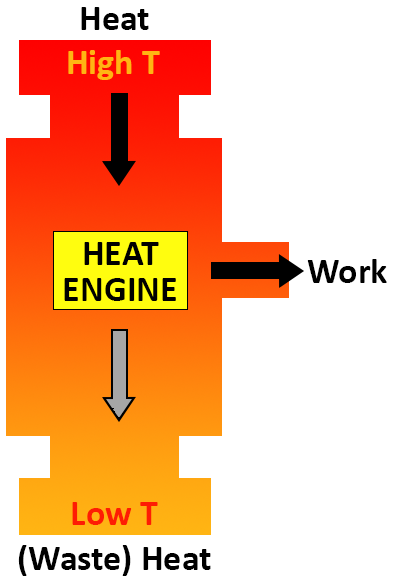
The Carnot Efficiency
A general expression for the efficiency of a heat engine can be written as:
We know that all the energy that is put into the engine has to come out either as work or waste heat. So work is equal to Heat at High temperature minus Heat rejected at Low temperature. Therefore, this expression becomes:
Where, QHot = Heat input at high temperature and QCold= Heat rejected at low temperature. The symbol (Greek letter eta) is often used for efficiency this expression can be rewritten as:
The above equation is multiplied by 100 to express the efficiency as percent.
French Engineer Sadi Carnot showed that the ratio of QHighT to QLowT must be the same as the ratio of temperatures of high temperature heat and the rejected low temperature heat. So this equation, also called Carnot Efficiency, can be simplified as:
Note: Unlike the earlier equations, the positions of Tcold and Thot are reversed.
The Carnot Efficiency is the theoretical maximum efficiency one can get when the heat engine is operating between two temperatures:
- The temperature at which the high temperature reservoir operates ( THot ).
- The temperature at which the low temperature reservoir operates ( TCold ).
In the case of an automobile, the two temperatures are:
- The temperature of the combustion gases inside the engine ( THot ).
- The temperature at which the gases are exhausted from the engine ( TCold ).

It's like taxes. The more money you earn (heat), the more money is taxed (cold), leaving you with less money to take home (efficiency). However, if you could earn more money (heat) and find a way to have less taxes taken out (better engine material), you would have more money to take home (efficiency).
Below is a table showing two temperature scales. The scale labeled "HOT," shows the range of temperatures for the combustion of gases in a car engine. The scale labeled "COLD," shows the range of temperatures at which gases are exhausted from the car engine.
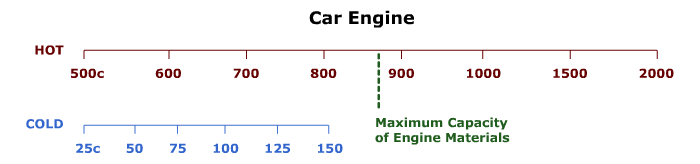
Instructions: Look carefully at the efficiency numbers in the body of the table. How do the Hot and Cold temperatures' effect on the efficiency.
| Hot 500°C |
Hot 600°C |
Hot 700°C |
Hot 800°C |
Hot 900°C |
Hot 1,000°C |
Hot 1,500°C |
Hot 2,000°C |
|
|---|---|---|---|---|---|---|---|---|
| Cold 150°C |
45 | 52 | 57 | 61 | 64 | 67 | 76 | 81 |
| Cold 125°C |
49 | 54 | 59 | 63 | 66 | 69 | 78 | 82 |
| Cold 100°C |
52 | 57 | 62 | 65 | 68 | 71 | 79 | 84 |
| Cold 75°C |
55 | 60 | 64 | 68 | 70 | 73 | 80 | 85 |
| Cold 50°C |
58 | 63 | 67 | 70 | 72 | 75 | 82 | 86 |
| Cold 25°C |
61 | 66 | 69 | 72 | 75 | 77 | 83 | 87 |
Answer the following questions based on the information in the Car Engine Efficiency table above.
Example
For a coal-fired utility boiler, the temperature of high pressure steam (Thot)would be about 540°C and Tcold, the cooling tower water temperature, would be about 20°C. Calculate the Carnot efficiency of the power plant:
Solution:
Carnot efficiency depends on high temperature and low temperatures between which the heat engine operates. We are given both temperatures. However, the temperatures need to be converted to Kelvin:
Practice
For a coal fired utility boiler, the temperature of high pressure steam would be about 540 degrees C and Tcold, the cooling tower water temperature, would be about 20 degrees C. Calculate the Carnot efficiency of the power plant.
Step 1
Convert the high and low temperatures from Celsius to Kelvin:
Step 2
Determine the efficiency using the Carnot efficiency formula:
From the Carnot Efficiency formula, it can be inferred that a maximum of 64% of the fuel energy can go to generation. To make the Carnot efficiency as high as possible, either Thot should be increased or Tcold (temperature of heat rejection) should be decreased.
Practice Problem
Use the following link to generate a random practice problem [4].
Entropy and Quality of Energy
Let’s look at an example of how temperature differences are used to generate power. Power plants convert chemical energy into electrical power. Here is a video overviewing the operation of a geothermal energy system, a classic thermal power generation plant.
You may have relaxed in a natural hot springs pool.
Or seen the old faithful geyser blasting hot water into the air in yellowstone national park. But have you ever thought of where all that heat comes from?
Well, it comes from deep beneath the surface of the earth -- and it's called geothermal energy...
And we can use it to generate clean renewable electricity. Ok, here's how geothermal works.
Heat from the earth's crust warms water that has seeped into underground reservoirs. When water becomes hot enough it can break through the earth's surface as steam or hot water. This usually happens where the earth's crust or 'plates' meet and shift.
In the past, taking advantage of geothermal energy was limited to areas where hot water flowed near the surface. But, as geothermal technologies advance, we can leverage even more of these natural renewable energy sources. Engineers have developed a few different ways to produce power from geothermal wells drilled into the ground.
Have a look at this. It's a dry steam geothermal power plant and it's the most common type of geothermal technology used today... Underground steam flows directly to a turbine to drive a generator that produces electricity. Pretty straightforward.
Another geothermal technology is called a flash steam power plant. A pump pushes hot fluid into a tank at the surface, where it cools. As it cools the fluid quickly turns into vapor-- or "flash" vaporizes. The vapor then drives a turbine -- and powers a generator.
A binary cycle plant works differently.
It uses two types of fluid. Hot fluid from underground heats a second fluid, called a heat transfer fluid, in a giant heat exchanger. The second fluid has a much lower boiling point than the first fluid and so it 'flashes' into vapor at a lower temperature. When the second fluid flashes... It spins a turbine that drives a generator.
The environmental benefits of this clean, round-the-clock renewable energy source are substantial: low emissions, small physical footprint, and minimal environmental impact. The few byproducts that can come up are often re-injected underground.
Geothermal energy can also help recycle wastewater. In california, wastewater from the city of santa rosa is injected into the ground to generate more geothermal energy.
Some plants do produce solid waste, but that solid waste may contain minerals that we can remove and sell... Which lowers the cost of this energy source.
The u.s. geological survey estimates that untapped geothermal resources in the united states, if developed, could supply the equivalent of 10% of today's energy needs. In fact, electricity generated by geothermal energy already provides about 60% of the power along the northern california coast...
From the golden gate bridge to the oregon state line.
Geothermal energy... ...helping to push america toward energy independence, and a clean, renewable way to meet our growing energy demands...
Below are two temperature scales. The scale labeled "HOT," shows the range of temperatures for the combustion of gases in a power plant. The scale, "COLD," shows the range of temperatures at which gases are exhausted from the power plant.

Instructions: Look carefully at the efficiency numbers in the body of the table. How do the Hot and Cold temperatures' effect on the efficiency.
| Hot 350°C |
Hot 400°C |
Hot 500°C |
Hot 600°C |
Hot 700°C |
Hot 800°C |
Hot 900°C |
Hot 1,000°C |
|
|---|---|---|---|---|---|---|---|---|
| Cold 300°C |
8 | 15 | 26 | 34 | 41 | 47 | 51 | 55 |
| Cold 250°C |
16 | 22 | 32 | 40 | 46 | 51 | 55 | 59 |
| Cold 200°C |
24 | 30 | 39 | 46 | 51 | 56 | 60 | 63 |
| Cold 150°C |
32 | 37 | 45 | 52 | 57 | 61 | 64 | 67 |
| Cold 100°C |
40 | 45 | 52 | 57 | 62 | 65 | 68 | 71 |
Answer the following questions based on the information in the Power Plant Efficiency table above.
Overall Efficiency
Calculating Overall Efficiency
Using the energy efficiency concept, we can calculate the component and overall efficiency:
Here the electrical energy is given in Wh and Chemical Energy in Btus. So Wh can be converted to Btus knowing that there are 3.412 Wh in a Btu.
This overall efficiency can also be expressed in steps as follows:
Applying this method to the above power plant example:
It can be seen that the overall efficiency of a system is equal to the product of efficiencies of the individual subsystems or processes. What is the implication of this?
Steps of Overall Efficiency
We have been looking at the efficiencies of an automobile or a power plant individually. But when the entire chain of energy transformations is considered—from the moment the coal is brought out to the surface to the moment the electricity turns into its final form—true overall efficiency of the energy utilization will be revealed. The final form at home could be light from a bulb or sound from a stereo. The series of steps as shown in the figure below are: 1) Production of coal (Mining), 2) Transportation to power plant, 3) Electricity generation, 4) Transmission of electricity, and 5) Conversion of electricity into light (Use).
We know what the cumulative efficiency is actually. We looked at that in the previous diagram. We talked about it. On this diagram, we are looking at cumulative or overall efficiency for a qualified power plant. Basically, in the ground, we have coal, right? We have to bring the coal out to the surface. That step is called mining. Obviously, we need to spend some energy to bring the coal from the ground to the surface. So mining by itself has some kind of, let's say, about 95% efficient. Or that step is 95% efficient. In other words, if we have 100 units in the ground, and by the time this energy comes out to the surface, we will be left with only 95 units. Because five units, we will be spending in operating the equipment and in bringing the coal from the ground to the surface. Now, this 95 obviously is not readily available, because we need to take these 95 BTUs to a power plant. So the trucks have to use some energy to take these 95 BTUs all the way up to the power plant. So when it reaches the power plant, these 95 units may turn out to be 90 units. In other words, we will be spending about five units in the transportation. So once we put in 90 units into a power plant, which is roughly about by now 33% efficient or 35% efficient, what this tells us is when we put in 90 units into the power plant, the output from the power plant in the form of electricity is only 30 units. So now, at this point, we have only 30 units left over when we started our business with 100 units. Now, these 30 units are transported through these high voltage lines to a user. By the time you get to the user, we're talking about a unit or two lost. All right? And now, when we have about, let's say for simplicity purposes we will still have about 29 units or 30 units. And as you all know, the efficiency of a light bulb is notoriously low. It's about 5% efficient. Which means that out of these 29 units or 30 units that we will get into the home, only 5% of that, or 1.5 units are converted, really, to the light. So we started off with 100, and we ended up with 1.5 units of light. So that means the overall efficiency is 1.5 divided by 100. Both are BTUs here. So the overall efficiency is only 1.5%. That is pathetically low. Which means to use 1.5 units of light, we are taking from Mother Earth 100 units. And along the way, we are dumping about 98.5 units of energy during various steps of conversion processes, and we're using 1.5 BTUs and 1.5%. That is the message.
Efficiency of a Light Bulb
If the efficiency of each step is known, we can calculate the overall efficiency of production of light from coal in the ground. The table below illustrates the calculation of overall efficiency of a light bulb.
| Step | Step Efficiency | Cumulative Efficiency or Overall Efficiency |
|---|---|---|
| Extraction of Coal | 96% | 96% |
| Transportation | 98% | 94% = (0.96 x 0.98) * 100 |
| Electricity Generation | 35% | 33% = (0.94 x 0.35) * 100 |
| Transmission of Electricity | 95% | 31% = (0.33 x 0.95) * 100 |
| Lighting: Incandescent Bulb |
5% | 1.6 % = (0.31 x 0.05) * 100 |
| Lighting: Fluorescent Bulb |
60% | 18 % = (0.31 x 0.60) * 100 |
Efficiency of an Automobile
A similar analysis on automobile efficiency is shown in the Figure below.
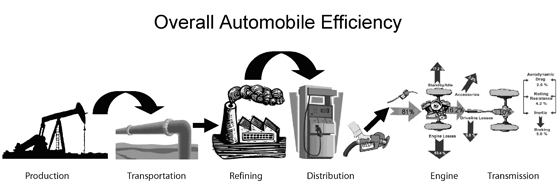 >
>
The table below shows that only about 10% of the energy in the crude oil in the ground is in fact turned into mechanical energy moving people.
| Step | Step Efficiency | Cumulative Efficiency or Overall Efficiency |
|---|---|---|
| Extraction of Crude | 96% | 96% |
| Refining | 87% | 84% |
| Transportation | 97% | 81% |
| Engine | 25% | 20% |
| Transmission | 50% | 10% |
Review and Extra Resources
Review
Please watch the 5:30 Lesson 3 Review below:
Hello everyone.
This is our review session for uh chapter three in this course where we're learning about energy efficiency and energy uh conversion processes.
So the real key of this chapter here is this one equation. And this is the one equation that i will not provide in the exams or in the sheets because i want you to memorize it because it is at the heart of this whole of this whole uh course. So useful energy out over total energy in is our energy efficiency.
Now remember the total energy in will always equal the total energy out, but many of it will be in forms that are not useful. So what that means is essentially we consume some primary energy source and then a fraction of that total energy we're putting in goes to something that we want it to. okay and it's always going to be less.
So whether we are moving the wheels on our car, we're trying to heat something up so that we can cook it the total energy in and that usefUl portion we're using to do some work it will be less.
Okay and so in each case we want to identify because there will be many energy outputs right and that's the first law of thermodynamics that the total energy in must always equal the total energy out. You cannot create or destroy energy and that's what's really encompassed in this first bullet here. All the energy we put in does not come out in the desired form. No such thing. An important thing to note when using this equation is that the energy should have the same units.
So you can't put joules in here and then say quads or btus or calories in here because the unit conversions will give you strain strange values for this efficiency. So it's really important when you use this to make sure that the units in both the top and the bottom match.
Another important note is that temperature of a substance is not a measure of its heat content. That's that's actually something that's energy related but instead it's the average kinetic energy of the molecules in their motion. Okay, one of the classic examples that was used long long ago to try to identify this equation and to describe it and what started the industrial revolution is the heat engine which is essentially a device that converts thermal energy into mechanical energy. So this comes up in our everyday lives well it used to come up more but as batteries and electrical energy conversion processes are coming in maybe it'll come up a bit less as we turn off of fossil fuels but still there are a lot of classic examples we can see.
Cars for example we take a gasoline which is chemical energy we then burn it to create thermal energy and then that thermal energy ends up spinning uh the wheels on our car or the blades on our lawn mowers. Right and it also works in a larger scale for coal and natural gas power plants when they're moving a turbine.
So these heat engines are described by the carnot efficiency which is a classic equation to tell us the limit of the absolute most energy we can get out of the thermal energy source. Right um to use this equation properly all the temperatures must be in kelvin. This is really important when you're ever dividing temperatures kelvin should always be used. And then you can see some clear relations with carnot efficiency that lets you know how a heat engine can be more or less efficient. A lot of that has to do with the temperature temperatures that are you're using right.
And so many of these principles are the key uh the key building blocks behind the workings of a power plant and as we had mentioned before right this thermal energy to mechanical energy isn't really one step but in fact in a total power plant there are many steps. Right so we have to go often from chemical energy to thermal energy to mechanical energy and then from mechanical energy we go to electrical energy and that's what we use to power our laptops and keep the lights on. And the way that we account for that is we essentially use our energy efficiency equation and we do that for each of those steps and then we multiply the efficiency of those steps together and that tells us our overall efficiency of the process. Right so what is the efficiency of going from chemical to thermo again it will never be a hundred percent so some will be we lost. And then from that useful thermo how much is going into mechanical and etc etc.
Okay so please take some time to review each of these key key points in this lecture and good luck on the quiz.
Okay.
Review Sheet Lesson 3 – Energy Efficiency
- Energy Conversion
- All the energy that we put in may not come out in the desired form
- Efficiency = Useful Energy Output / Total Energy Input
- Both energies must in the same units
- The temperature of a substance is not a measure of its heat content, but rather, the average kinetic energy of its molecules resulting from their motions
- Heat Engine
- Device that converts Thermal energy into Mechanical energy
- Carnot Efficiency
- All temperatures must be in Kelvin
- As Tlow decreases, efficiency increases. As Tlow increases, efficiency decreases
- As Thot decreases, efficiency decreases. As Thot increases, efficiency increases
- Workings of a Power plant
- Overall Efficiency = product of step efficiencies
Test Yourself
The questions below are your chance to test and practice your understanding of the content covered in this lesson. In other words, you should be able to answer the following questions if you know the material that was just covered! If you have problems with any of the items, feel free to post your question on the unit message board so your classmates, and/or your instructor, can help you out!
- A heat engine has Carnot efficiency of 30%. Useful output from the engine is 1000J. How much heat is wasted?
- How can we improve the Carnot efficiency of a heat engine by changing the hot and cold reservoir temperatures?
- Most of the energy conversion devices that we use in our day-to-day life can be classified as Heat Engines. Give two examples.
Extra Resources
For more information on topics discussed in Lesson 3, see these selected References:
- Hinrichs, R. A., “Energy,” Saunders College Publishers, Philadelphia, PA, 1992.
- Aubrecht, G. L., “Energy,” Prentice Hall, Inc., Englewood Cliffs, NJ, 1995.
- Fay, J.A. and Golomb, D. S., “Energy and the Environment,” Oxford University Press, New York, NY, 2002.
- Christensen, J. W., “Global Science: Energy Resources Environment."
Lesson 3 Deliverables
Deliverable 1
You must complete a short quiz that covers the reading material in lesson 3. The Lesson 3 Quiz, can be found in the Lesson 3: Energy Efficiency module in Canvas. Please refer to the Calendar in Canvas for specific time frames and due dates.