Lesson 7: Home Heating Basics
The links below provide an outline of the material for this lesson. Be sure to carefully read through the entire lesson before returning to Canvas to submit your assignments.
Introduction
Welcome to Lesson 7!
We are into Lesson Seven now: home heating basics. This is a very interesting and very important chapter. Let me warn you about one thing: this chapter has a lot of calculations, and in the entire course this is the most, I would say, calculation-oriented chapter. So I want you to pay attention to this one.
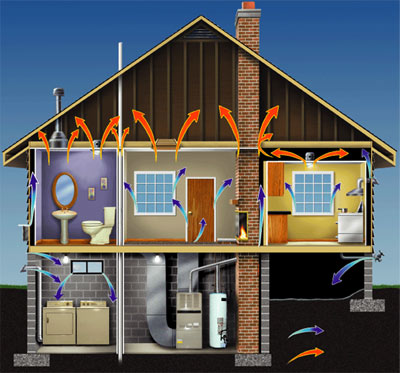
Basically, if you have a house, you will be losing (or gaining) heat from various places like windows, like the ceiling, the roof, the walls, the doors, through the floor, everywhere. So in this chapter, we will be looking at how much heat transfer occurs and by what means you will be losing or gaining it. Let's say we have this wonderful mansion, and we want to keep the interior at, let's say, 70 degrees all the time. And we have a little furnace that puts out heat and that keeps the interior at 70 degrees even when outside it's, let's say, 10 degrees Fahrenheit. Heat always tends to get out. It can actually go through those solid walls, or if we have windows, it can go through windows or even the roof. And when you open doors and windows, air might leak in and out, so that's another way of losing heat. So there are several ways in which heat is lost to the outside.
How much heat the furnace has to put out to keep the temperature constantly at 70 degrees inside can easily be calculated or known when we know how much heat is escaping. If somehow, ideally, we can seal off this entire place without any heat loss, then once you bring this house to 70 degrees you can turn on the furnace, and it will remain at 70 degrees for the rest of the season. But you and I both know that is not the case. So in this chapter, you're going to learn how much heat is escaping through various surfaces here. And obviously, whatever is escaping, that is the amount of energy that the furnace has to put out. Which means we have to buy energy and put it into the furnace in the form of fuel. So if we are losing a million BTUs like this through all these areas, we have to get a million BTUs made up from this furnace. And we also know that the furnaces are not 100% efficient, either. If we need to get 100,000 BTUs, or 1 million BTUs from the furnace, we cannot expect a furnace to put out if we put in 1 million BTUs. So if we want 1 million BTUs as output, obviously we have to put more in, in the form of fuel. So to know how much fuel we have to put in, we have to know how much heat loss we actually have in the house.
So we will be looking at residential heat loss, how to calculate that, and in what ways we lose heat in this first chapter of Lesson Seven. We will understand the mechanisms of heat transfer and also calculate the heating degree days for a heating season, which is basically the number of degrees that we have to heat our air. If the outside temperature is low, obviously we have to heat our air to a higher temperature or higher number of degrees. That's more degrees of heating. So we will calculate how many degrees we have to heat per day and per season, and so on and so forth. And if we know that, we can calculate the heat loss from a solid wall. That is conduction heat loss. We will talk about conduction, convection, and radiation -- those three mechanisms of heat loss.
And also, once we have a wall, not all walls are the same. Some walls resist more heat loss than the others. So we define a property of a wall, a property of a solid material, that tells us how much the material resists the heat loss. That's called R-value. So we will understand and articulate the concept of R-value here. And we can also increase the R-value of a wall by increasing its thickness or by going to a different material, and so on. And if we were to have a wall with lower R-value, which means lower resistance, we would be losing more heat to the outside. And we would be requiring more heat or more fuel to heat that place. So we'll talk about the cost of various fuels for a given heat loss. Seeing 1 million BTUs that we lose, if we were to heat with natural gas to get that same 1 million BTUs, what would it cost? Or if we use electricity, what would it cost to get 1 million BTUs? Or if we use propane, what would it cost? But the heat loss is always 1 million BTUs. For the same amount of heat loss, which fuel happens to be cheaper fuel or more expensive fuel? That's what we will be determining here.
We will also understand that if we have to install more insulation, we will need to borrow more money. And if we borrow more money and put in more insulation, can we save enough through heat loss to pay back that money that we borrowed? That is payback period. You already know the concept. We will do some calculations to see whether it is wise to borrow money and put more into insulation. All right, that's basically part A here. And we will also look at part B, which is insulation and home heating fuels. And in this part, we will talk about various types of insulation materials and how we can improve a wall's performance by adding more and more layers to that wall. So if we have a wall that has four different materials together, we'll see that, for example, inside we would have drywall that we could paint easily. And behind the drywall we have the framework, like a wooden frame with wooden studs that are used for structural integrity. And between those studs, you always pack some insulation material. And outside the insulation material is not visible because we'll have a plywood or sheathing outside. And even sheathing doesn't look good outside, so on top of that we put a siding, a vinyl siding or brick or whatever it is.
So when we have different materials together, one right behind the other, they will all together resist the heat loss. So we will calculate the heat loss resistivity or R-value of a wall that has different layers of insulation. And if we have that, we can find how much energy we can save or how we can cut the heat loss, et cetera. And also we will talk about the efficiencies, the furnaces, and how we can distribute the heat in the house into various rooms, et cetera, of different heating systems. We'll talk about that later on in the next chapter. So this is basically a calculation-oriented and problem-based kind of chapter or lesson. And if we have any more difficulties in this one, I also added on top of this the practice questions, a bunch of practice problems which explain you how to do numerical problems. For example, I have given here a bunch of problems, actually, using the formulas that we'll be looking at here for practice. There are a bunch of problems -- about 30 problems or so.
Those of you who are comfortable with the material can do these problems yourselves and see if you got them correct by going to this answers page, where the same problems are given with answers. So you can actually look at whether you got the same answer or not. If you got it right, you are happy. If you don't, you may feel lost. If that's the case, what you do is click on this third one here, where for every problem we have a solution, actually, like audio that I'm speaking to you right now. I have made some movies again for each of these problems that will explain to you like a blackboard, or white board rather.
So there are a bunch of problems like this that you can look at. And most of the problems have solutions like this. So I've tried to make your life simpler. Lesson Seven is a two-week lesson, which means you will have a quiz at the end of two weeks after the lesson is assigned. And you take the quiz at the end of the lesson.
Good luck.
Home Heating
Home heating is the single highest energy expense for a household.
- Energy spent for residential space heating accounts for about 10 percent of the total energy consumed in the United States.
- The average household consumes 92 million BTUs, and 46 percent of that is used for home heating.
- According to EnergyStar.gov [1], average annual energy expenses were $2,060. Home energy use also accounted for 20 percent of the greenhouse gas emissions.
Therefore, reduction of energy consumption in home heating results in substantial monetary savings and reduction in air pollution. With appropriate improvements, average home heating costs can be reduced by 30 percent (i.e., about $500 a year).
| Appliances | Percentage |
|---|---|
| Space Heating | 29% |
| Air Conditioning | 13% |
| Water Heating | 13% |
| Appliances including refrigerator, dish washer and clothes washer | 12% |
| Lighting | 12% |
| Other Electronics | 21% |
Lesson 7 Objectives
Upon completing this lesson, you will be able to:
- understand the mechanisms of heat transfer;
- calculate heating degree days for a heating season and articulate significance of Heating Degree Days (HDD);
- calculate heat loss from a home using conduction equation;
- understand the concept of R-value and its importance in home heating;
- compare the cost of various fuels for a given heat loss;
- understand the significance and be able to calculate the pay-back period.
Questions?
If you have any questions, please post them to the General Course Questions forum in located in the Discussions tab in Canvas. I will check that discussion forum daily to respond. While you are visiting the discussion board, feel free to post your own responses to questions posted by others - this way, you might help a classmate!
Lesson 7a: Residential Heat Loss
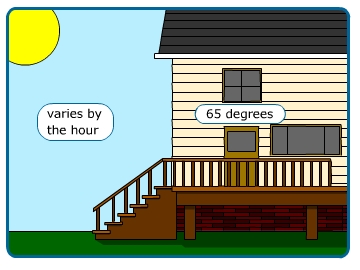
Houses are heated to keep the temperature inside at about 65°F when the outside temperature is lower. A house requires heat continuously because of the heat loss. Heat can escape from a house through various places; some are well known and some are not noticeable. Heat can escape from the roof, walls, doors, windows, basement walls, chimney, vents, and even the floor.
The more heat the house leaks, the more the furnace has to put out to make up for the loss. For the furnace to generate more heat to compensate the heat loss, more fuel needs to be put into the furnace, hence higher fuel or heating costs.
As you will recall from Lesson 3, not all energy conversion devices are efficient. Thus, it is important to note that furnaces are not 100 percent efficient. When a furnace’s efficiency is lower, the fuel consumption for the same amount of heat output will be even higher.
Where Does Heat Loss Occur?
Participate in the following activity to find out where the most heat loss occurs.
- Drag and drop the percentages onto the appropriate area of the home indicating where heat loss occurs.
Where Does Heat Loss Occur?
Below are the most common places for heat loss in a typical home.
- Heat loss through ceilings.
- Heat loss through windows.
- Heat loss through doors.
- Heat loss through frame walls.
- Heat loss through cracks in walls, windows, and doors.
- Heat loss through basement walls.
- Heat loss through basement floor.
Question: Which one has the most heat loss compared to the others?
Answer: # 5 Heat loss through cracks in walls, windows, and doors
Actual percentages of heat loss for each:
- Heat loss through ceilings = 5%
- Heat loss through windows = 16%
- Heat loss through doors = 3%
- Heat loss through frame walls = 17%
- Heat loss through cracks in walls, windows, and doors = 38%
- Heat loss through basement walls = 20%
- Heat loss through basement floor = 1%
Mechanisms of Heat Loss or Transfer
Heat escapes (or transfers) from inside to outside (high temperature to low temperature) by three mechanisms (either individually or in combination) from a home:
- Conduction
- Convection
- Radiation
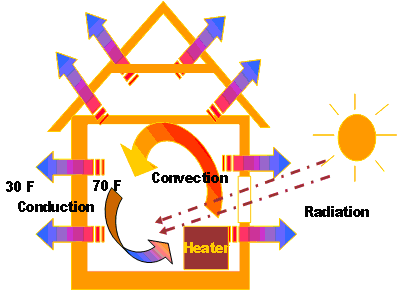
Click here to open a text description of the examples of heat transfer by conduction, convection, and radiation
- Conduction: heat moving through walls of a home from high temperature inside to low temperature outside.
- Convection: heat circulating within the rooms of a house.
- Radiation: Heat from the sun entering a home.
Conduction
Conduction is a process by which heat is transferred from the hot area of a solid object to the cool area of a solid object by the collisions of particles.
In other words, in solids the atoms or molecules do not have the freedom to move, as liquids or gases do, so the energy is stored in the vibration of atoms. An atom or molecule with more energy transfers energy to an adjacent atom or molecule by physical contact or collision.
In the image below, heat (energy) is conducted from the end of the rod in the candle flame further down to the cooler end of the rod as the vibrations of one molecule are passed to the next; however, there is no movement of energetic atoms or molecules.
Click the play button to start the animation.
Click here to open a text description of the Conduction Candle animation
Example of Conduction
A hand holds a metal rod above a lit candle. The molecules quickly heat up at the point where the flame touches the rod. The heat then spreads across the entire metal rod, and the heat is then able to be felt by the hand.
With regard to residential heating, the heat is transferred by conduction through solids like walls, floors, and the roof.
Click the play button to start the animation.
Click here to open a text description of Conduction in Regard to Residential Heating example
Example of Conduction in Regard to Residential Heating
Picture the cross-section of a wall in a house. Inside the house it is 65°F and outside it is 30°F. Two arrows point from inside the house to the outside to show how heat is transferred from the inside of the house to the outside through the wall via conduction.
Convection
Convection is a process by which heat is transferred from one part of a fluid (liquid or gas) to another by the bulk movement of the fluid itself. Hot regions of a fluid or gas are less dense than cooler regions, so they tend to rise. As the warmer fluids rise, they are replaced by cooler fluid or gases from above.
In the example below, heat (energy) coming from candle flame rises and is replaced by the cool air surrounding it.
Click the play button to start the animation.
Click here to open a text description of the Convection Candle animation
Example of Convection
A hand is held above a lit candle. As the candle heats the air, the heat rises to the hand. Eventually, it gets too hot, and the hand pulls away from the candle.
In residential heating, convection is the mechanism by which heat is lost by warm air leaking to the outside when the doors are opened, or cold air leaking into the house through the cracks or openings in walls, windows, or doors. When cold air comes in contact with the heater in a room, it absorbs the heat and rises. Cold air, being heavy, sinks to the floor and gets heated, and thus slowly heats the whole room air.
Instructions: Press the play button below and observe what happens to the cold air (blue arrows) as it enters the house and encounters the warm air (red arrows) coming from the heating vent:
Click here to open a text description of the Convection in a Room animation
Example of Convection in Regard to Residential Heating
Picture a room with an open door letting in cool air on the left and a radiator creating heat on the right. As the radiator heats the air around it, the air rises and is replaced by cool air. Once the warm air hits the ceiling, it travels left towards the open door, cooling as it moves. The cool air from the open door travels to the right across the floor towards the radiator to be heated. The overall effect is a circular convection current of air within the room.
Radiation
Radiation is the transfer of heat through electromagnetic waves through space. Unlike convection or conduction, where energy from gases, liquids, and solids is transferred by the molecules with or without their physical movement, radiation does not need any medium (molecules or atoms). Energy can be transferred by radiation even in a vacuum.
In the image below, sunlight travels to the earth through space, where there are no gases, solids, or liquids.
Click the play button to start the animation.
Click here to open a text description of the Radiation Example animation
Example of Radiation
Picture the Sun and the Earth, with arrows traveling from the Sun to the Earth through space. The arrows represent the energy that travels to the Earth via radiation, which does not require any medium (atoms or molecules) to do so.
Test Yourself
First, identify the type of home heat loss pictured in images A-J as either: conduction, convection or radiation. Then click and drag each image down to the correct category at the bottom of the screen.
Click here to open a text description of the Test Yourself activity
Test Yourself: Types of Heat Loss
Identify the type of heat loss (conduction, convection, or radiation) for each of the following examples:
- Heat escaping through the roof of a house
- A hot stove burner
- Boiling water
- A torch halogen lamp producing light and heat
- A door hanging wide open, letting in cold air
- A fire creating heat
- Heat escaping through a wall
- A mirror reflecting sunlight
- Heat escaping through a window
- Heat escaping through a chimney
Answers:
A. Conduction
B. Radiation
C. Convection
D. Radiation
E. Convection
F. Radiation
G. Conduction
H. Radiation
I. Conduction
J. Radiation
Reducing Energy Consumption
There are two ways in which we can reduce energy consumption.
- The most cost-effective way is to improve the home’s “envelope”—the walls, windows, doors, roof, and floors that enclose the home—by improving the insulation (conduction losses) and sealing the air leaks with caulking (convection losses).
- The second way to reduce the energy consumption is by improving the efficiency of the furnace that provides the heat.
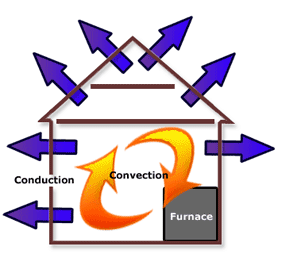
Click here to open a text description of the Conduction and Convection diagram
Line drawing of a house with arrows pointing out from the walls and roof showing conduction & arrows flowing in a circular motion inside the house showing convection.
Conduction Heat Loss
Main Factors of Heat Loss
What does a house's heat loss depend on? Complete the activity below to find out the three main factors leading to heat loss.
Main Factors of Heat Loss
What are the three main factors a house's heat loss depends on?
Example 1:
House A sits next to house B. Though both houses have the same basic design, house B is significantly larger than house A.
- Which house loses more heat?
- House A
- House B
- Why do you think this house loses more heat?
- More people in it
- More appliances and lights are used
- Larger size/more area
Example 2:
House A and house B are the exact same size and design. House A sits on the beach in a warm, tropical area, while house B sits by a ski resort in the mountains up north, surrounded by snow.
- Which house loses more heat?
- House A
- House B
- Why do you think this house loses more heat?
- People skiing need more heat to keep warm
- Snow on the roof is good insulation
- Outside temperature
Example 3:
House A and house B are the same size and sit next to each other. The design for both houses is the same, except house A has a thick layer of pink insulation installed. The R-value of house B is .63 and the R-value of house A is unknown.
- Which house loses more heat?
- House A
- House B
- Why do you think this house loses more heat?
- Less insulation
- It's only one color
- It's thicker
Answers:
Example 1:
- B: House B
- C: Larger size/more area
Example 2:
- B: House B
- C: Outside temperature
Example 3:
- B: House B
- A: Less insulation
Most heat is lost through a house's walls through conduction. As you learned from the activity on the previous screen, the amount of heat loss depends on three factors:
- Size of the house (area through which the heat can escape)
- Local weather or climatic conditions:
- The inside temperature is often constant at a comfortable temperature of 65°F.
- As the outside temperature falls lower than 65°F, the heat is lost to the outside.
- The higher the temperature difference, the higher the heat loss to outside.
- By calculating the Heating Degree Days (HDD), we can determine how many degrees the mean temperature fell below 65ºF for the day.
- Wall's capacity to resist heat loss.
- Insulation is rated in terms of thermal resistance, called R-value, which indicates the resistance to heat flow.
- The higher the R-value, the greater is the insulating effectiveness.
Heating Degree Days
Local weather or climatic conditions are one of three factors that affects the amount of heat loss through conduction. When examining weather conditions, we look at both the inside and outside temperature of a home.
The inside temperature is usually taken as a standard comfort temperature of 65ºF. The outside temperature varies by the hour. Knowing this information can help us to understand two concepts:
- Average outside temperature = Average of the maximum and minimum temperature during the day
- Heating Degree Day (HDD) = The temperature difference through which air has to be treated, or how many degrees the mean temperature fell below 65ºF for the day. It is also an index of fuel consumption.
Determining Heating Degree Day (HDD)
The formula for determining the Heating Degree Day (HHD) is:
To calculate HDD:
- Determine the base temperature or inside temperature:
- Find the day's average outside temperature using this formula:
- Use the HDD formula to solve:
Try This!
Click the play button below, and observe the temperature changes. Then calculate the average temperature and the Heating Degree Day.
Click here to open a text description of the Heating Degree Days activity.
Try This: Determining Heating Degree Day (HDD)
Picture a house with a thermometer on the porch. The current outside temperature is 60 degrees. As thick clouds start to move in, the temperature begins to drop in 5 degree increments, first to 55 degrees, then 50 degrees, etc. When the clouds have completely blocked the Sun, the thermometer reads 40 degrees.
Questions:
- What is the average temperature?
Hint: Ta = (max temperature + minimum temperature) divided by 2. - What is the heating degree days?
Hint: HDD = Tbase - Ta
Answers:
- 50 degrees
- 15 degrees
Heating Degree Days Examples
Example 1
Calculate the HDD for one day when the average outside temperature is 13º F.
Calculate the HDD for one day when the average outside temperature is 2º C.
Example 2
Given the following data, calculate the HDD for the week:
| Day | Average Temperature |
|---|---|
| Sunday | 49° F |
| Monday | 47° F |
| Tuesday | 51° F |
| Wednesday | 60° F |
| Thursday | 65° F |
| Friday | 67° F |
| Saturday | 58° F |
Heating Degree Day
For this problem, we need to calculate HDD for one full week. The data that is given is each day, what is the outside temperature -- average outside temperature. For example, Sunday, the average outside temperature is 49 degrees F. Monday 47 degrees Fahrenheit, Tuesday it’s 51 and Wednesday it is 60 degrees F and on Thursday it is 65, Friday, 67 and on Saturday it is 58.
| Day | Temperature (°F) |
|---|---|
| Sunday | 49 |
| Monday | 47 |
| Tuesday | 51 |
| Wednesday | 60 |
| Thursday | 65 |
| Friday | 67 |
| Saturday | 58 |
So we need to calculate heating degree days (HDD) for each day. One day, that is Sunday, the outside temperature is 65 minus 49 the outside temperature will give you the degree days. Similarly, 65 minus 47° Fahrenheit, one day times 65 minus 51 in this case. One day times 65 minus 60 and one day 65 minus 65. This would be zero. One day 65 minus 67. Remember when it exceeds 65, the heating degree days would be zero. In this case, also it is zero. One day on Saturday it is 65 minus 58.
| Day | Temperature (°F) | Calculate HDD |
|---|---|---|
| Sunday | 49 | 1 day (65-49) |
| Monday | 47 | 1 day (65-47) |
| Tuesday | 51 | 1 day (65-51) |
| Wednesday | 60 | 1 day (65-60) |
| Thursday | 65 | 1 day (65-65)=0 |
| Friday | 67 | 1 day (65-67)=0 |
| Saturday | 58 | 1 day (65-58) |
This case it is 7.
| Day | Temperature (°F) | Calculate HDD |
|---|---|---|
| Sunday | 49 | 1 day (65-49)=16 |
| Monday | 47 | 1 day (65-47)=18 |
| Tuesday | 51 | 1 day (65-51)=14 |
| Wednesday | 60 | 1 day (65-60)=5 |
| Thursday | 65 | 1 day (65-65)=0 |
| Friday | 67 | 1 day (65-67)=0 |
| Saturday | 58 | 1 day (65-58)=7 |
These two are zeros, this is 5 and this is 14 and this happens to be 18 and here it is 16. So the total sum is for one full week is 60 degree days.
| Day | Temperature (°F) | Calculate HDD |
|---|---|---|
| Sunday | 49 | 1 day (65-49)=16 |
| Monday | 47 | 1 day (65-47)=18 |
| Tuesday | 51 | 1 day (65-51)=14 |
| Wednesday | 60 | 1 day (65-60)=5 |
| Thursday | 65 | 1 day (65-65)=0 |
| Friday | 67 | 1 day (65-67)=0 |
| Saturday | 58 | 1 day (65-58)=7 |
| Total | 60 Degrees |
This is equal to 60 degree days.
Seasonal Heating Degree Days
In previous examples, we are assuming that the outside temperature remains the same for all 150 heating days in a season. This is not realistic, but it explains the method to calculate the HDD. In a more realistic example, we need to find the temperature difference for each day and add all the temperature differences.
We will now look at Seasonal Heating Degree Days (HDD), which is the sum of temperature differences of ALL days - rather than just 1 day or 1 week - during which heating is required.
The table below provides Seasonal HDDs for selected places in the United States. The higher HDD indicates a higher heat loss and therefore, higher fuel requirements.
HDD is used to estimate the amount of energy required for residential space heating during a cool season, and the data are published in local newspapers or on the National Weather Service website.
| Place | Degree Days |
|---|---|
| Birmingham, AL | 2,823 |
| Anchorage, AK | 10,470 |
| Barrow, AK | 19,893 |
| Tucson, AZ | 1,578 |
| Miami, FL | 155 |
| Pittsburgh, PA | 5,829 |
| State College, PA | 6,345 |
Source: NOAA [3]
Calculating Seasonal Heating Degree Days
To calculate Seasonal Heating Degree Days, use this formula:
Remember, in months where the average temperature is equal to or greater than 65, there will be no heating degree days, so the value for the month will be 0.
Seasonal Heating Degree Days Examples
Example 1
Given the following set of average temperatures, by month, for State College, PA, calculate the HDD for the heating season:
| Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 25°F | 28°F | 37°F | 48°F | 59°F | 67°F | 71°F | 70°F | 62°F | 51°F | 41°F | 31°F |
Please watch the following (2:32) presentation about problem #1:
Lesson 7a, Screen 23: Seasonal Heating Degree Days
Example 3
Given the following set of average temperatures, by month, for State College, PA, calculate the HDD for the heating season:
| Jan | Feb | Mar | Apr | May | Jun | July | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 °F | 28 °F | 37 °F | 48 °F | 59 °F | 67 °F | 71 °F | 70 °F | 62 °F | 51 °F | 41 °F | 31 °F |
Alright, this is an interesting problem. Given the following temperatures by month for State College, we need to calculate the heating degree days for the entire season. For January, the outside temperature is 25° F. This is average temperature for 31 days in January. And February, the outside temperature is 28° F, March, 37° F and April it is 48° F and May, the temperature outside is 59° F. June, the outside temperature is 67° F, July, the outside temperature is 71° F and August it is 70° F. September, it goes on like that. September it is 62° F, and October it is 51° F, November, 41° F and December goes as 31° F.
What we need to do is basically subtract this number (25° F) from 65 so the difference is, 65 minus 25, so this is 40° F for the month of January.
The same case here (February). 65 minus 28 which happens to be 37° F.
And if we do the same for all these months, from March through December, and then we have to multiply each month temperature difference by the number of days in the month.
So, for example, in the case of January, there are 31 days. So when you multiply 40◦ by 31 days you get 1240 degree days.
Similarly, we can do for all these months and add up and it turns out that for the entire year, it is 6138 degree days is for State College.
Example 2
If Ms. S. Belle moves from Birmingham, AL (HDD=2,800) to State College, PA (HDD=6,000) how much can she expect her heating bill to increase?
Please watch the following 1:34 presentation about problem #2:
Lesson 7a, Screen 24: Seasonal Heating Degree Days
Example 4
If Ms. S. Belle moves from Birmingham, AL (HDD = 2,800) to State College, PA (HDD=6,000) how much can she expect her heating bill to increase?
Alright, this is problem 1.6, if Ms. S. Belle moves from Birmingham, AL to State College, how much can she expect her heating bill to increase?
Birmingham, AL has heating degree days of 2800 and State College, PA has 6000. We need to remember this 6000 degree days. Basically what’s happening here is she is going to be heating more her home and it is increasing from 2800 to 6000. So, her increase is 6000 minus 2800 will be 3200 degree days.
And this increase (3200) is how much compared to 2800 what she has been paying for. So the increase is 3200 compared to the baseline of 2800. We need to multiply this by 100 to get the percentage. It would be an increase of 114 %.
She would be spending about 114% more for her heating in State College, PA.
Calculating Hourly Heat Loss
As we have learned, most heat is lost through a house's walls through conduction. One of the three factors that affect heat loss is a wall's capacity to resist heat loss.
We will now look at how to calculate the rate of heat loss of the walls of a house, using the following formula:
From the above equation, it can be seen that once the house is built, these two variables will NOT change:
- The area of the walls
- The R-value of the walls
The only variable that will change is the temperature difference between inside and outside.
Example
Calculate the heat loss for a 10 ft by 8 ft wall, insulated to R-value 22. The inside temperature is maintained at 70° F. The temperature outside is 43° F.
Please watch the following 2:25 presentation about Hourly Heat Loss:
Lesson 7a, Screen 26: Calculating Hourly Heat Loss
Example 5
Calculate the heat loss for a 10 ft by 8 ft wall, insulated to R-value 22. The inside temperature is maintained at 70°F. The temperature outside is 43°F.
For this problem, we are trying to calculate the heat loss. We are given the dimensions; we are given the R-value and the temperature difference. Those are the quantities that we need to calculate the heat loss, basically.
The dimensions are, the wall dimensions are 8ft and this side is 10 ft.
So the area is 8 times 10 will be 80 foot square or 80 square feet. And we are also given the inside temperature is 70°F and outside temperature, average outside temperature, is 43°F. Therefore, the difference or delta T (ΔT) is equal to 27°F.
Now area is given, A is, we already calculated 80ft2 and R-value is also given as 22 which is 22 ft2 °F hour over BTU.
Now, heat loss, BTUs per hour, is equal to area times ΔT divided by R-value.
Now in this case, it is:
So this will be equal to, here you can cancel ft2 and this ft2 and this °F and this °F, and we are left with BTUs per hour. And the heat loss comes out to be 98.2 BTU/h.
Calculating Daily Heat Loss
Now that you know how to calculate hourly heat loss, how would you calculate daily heat loss?
Since there are 24 hours in a day, you would simply multiply the hourly heat loss by 24.
Example
What is the hourly and daily heat loss of a 15-ft by 15-ft room with an 8-ft ceiling, with all surfaces insulated to R13, with inside temperature 65°F and outside temperature 25°F?
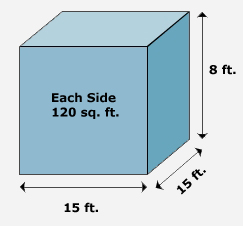
Once we know the heat loss rate per hour, we can determine the heat loss per day by multiplying by 24 (hours in a day).
In a 24-hour period or one day, the heat loss would be:

Area (ft2) is the sum of the area of all four walls. Each wall is 8' x 15', or 120 sq. feet, so take 4 x 120 sq ft to get 480 ft2 in the equation.
Calculating Annual Heat Loss
In the previous calculations, we determined hourly and daily heat loss. How do we calculate annual or seasonal heat loss?
Since the temperature outside the house may not remain the same day after day, the heat loss will vary by the day. Thus, to obtain the heat loss for a whole year, we do the following:
- Calculate heat loss for each day.
- Add the heat loss for all days in a year that needed heating.
- Leave the R-value of the wall and the area of the wall the same – they will not change.
- Determine the difference between inside and outside temperature, since it will change for each day.
Recall that the formula for daily heat loss is:
Thus, theoretically, we would need to perform this calculation for every day of the 365-day calendar year.
For example, if the average outside temperature were to be 35°F, 32°F, 28°F, and so on for each day, the heat loss for the whole year or the season can be calculated as follows:
Since the area (480 ft2), R-value ,and 24 h in a day are common for ALL heating days, we can bring those out and rewrite the equation as:
This equation can be even further simplified. The formula for Annual or Seasonal heat loss can be written in general terms as:
Calculating Annual Heat Loss Examples
Example 1
Please watch the following 3:29 presentation on Example Problem #1. For the 150-day heating season in Roanoke, VA, the average temperature was 47° F. How much heat is lost through a 176 ft2 wall (R=16) during the entire season?
Lesson 7a, Screen 32: Calculating Annual or Seasonal Heat Loss
Example 7 (formerly Example 3-11)
For the 150-day heating season in Roanoke, VA, the average temperature was 47°F.
How much heat is lost through a 176 ft2 wall (R=16) during the entire season?
Ok. In this problem, 3-11, we are trying to calculate the heat loss for a 150-day season in Roanoke, VA. It is a 150-day heating season. The outside temperature is given as 47°F. Inside, is obviously 65°F. Ok?
Outside: 47°F
Inside: 65°F
Degree Days can be calculated like this. Heating Degree Days are equal to the number of days, which is 150 in a season here, times the temperature difference. 65 minus 47°F.
Now we can calculate that. That is equal to 150 days times 18. So that turns out to be 2700 °F days.
Now, what else do we need? We need the area. Area is given. Area is equal to 176 ft2, and we are also given the R-value. R-value is 16.
Therefore, we can calculate the heat loss, heat loss through a season. Heat loss through the season is equal to Area times HDD times 24 over R.
Now, what can we cancel? ft2/ ft2, °F/°F, hour/hour and days/days are canceled. So when we do this calculation here, we get the answer of 712,800 Btus in this 150 day heating season.
Example 2
Please watch the following 3:42 presentation on Example Problem #2. In Fargo, ND, the heating season lasts about 220 days and the average outside temperature is around 27° F. How much heat is lost through an 8 ft by 6 ft window (R=1) during the heating season?
Lesson 7a, Screen 33: Calculating annual or Seasonal Heat Loss
Example 8 (formerly example 3-12)
In Fargo, ND, the heating season lasts about 220 days and the average outside temperature is around 27°F. How much heat is lost through an 8 ft by 6 ft window (R=1) during the heating season?
This problem is very similar to the last one, 3-11. Now this 3-12 involves again heat loss through a season. We need to calculate the HDD’s. The heating days are 220 days. Now the temperature difference is, inside, 65°F as usual and outside, the temperature, the average temperature happens to be 27°F for all 220 days. Therefore, Heating Degree Days (HDD) can be calculated like this: 220 days times (65°F minus 27°F). And this is equal to 220 days times 38°F which is equal to 8,360°F days.
Now, do we know the area? Area is given, actually. The dimensions of the window are 8ft by 6ft. Therefore the area is 8ft times 6ft, which is 48ft2
We know the temperature difference, we know the HDD, and we can calculate the heat loss provided we have the R value. R-value is also given. 1 ft2 °F h over BTU.
Now it is easy to calculate heat loss. Heat loss for the season is equal to area (and I am trying to repeat this), area times HDD times 24 over R. So in this case it is, area is 48 ft2 and we have 8360 degree days times 24 hours divided by a day over R value of 1 ft2 °F h/BTU.
So ft2/ft2, °F/°F will be canceled, hours and hours are canceled, days and days are canceled here.
So, when you do this math, it comes out to be 9,630,720 BTUs. This is in one full season.
Lesson 7b: Insulation and Home Heating Fuels
The following section of Lesson 7 wil discuss insulation and home heating fuels.
R-Value
As you may recall from the first part of this lesson, R-value is a wall's capacity to resist heat loss or its thermal resistance. Insulation materials are rated in terms of their R-value, with a higher R-value indicating better insulating effectiveness.
The R-value of thermal insulation depends on the type of material, its thickness, and its density. Generally, walls are not made up of just one material or one layer.
R-values for most commonly used building materials are given in the table below. From looking at the table below, we can see that natural materials like stone and bricks are not good insulation materials, but most of the synthetic insulation products such as polystyrene or polyurethane are very effective insulation materials.
| Material | R-Value (ft2 o F h / BTU) |
|---|---|
| Plain glass, 1/8 inch | 0.03 |
| Stone per inch | 0.08 |
| Common Brick per inch | 0.20 |
| Asphalt Roof Shingles | 0.44 |
| 1/2 inch Gypsum Board (Drywall or plasterboard) | 0.45 |
| Wood Siding, 1/2 inch | 0.81 |
| Plywood, 3/4 inch | 0.94 |
| Insulating sheathing, 3/4 inch | 2.06 |
| Fiberglass, per inch (battens) | 3.50 |
| Polystyrene per inch | 5.00 |
| Polyurethane Board | 6.25 |
If insulation materials have a low R-value per inch, then they will need to be thicker than those materials with a higher R-value per inch to achieve the same degree of effectiveness in resisting heat loss.
Look at the chart below to compare the thickness required of various insulation materials to achieve the same R-Value of 22 and then answer the questions below.
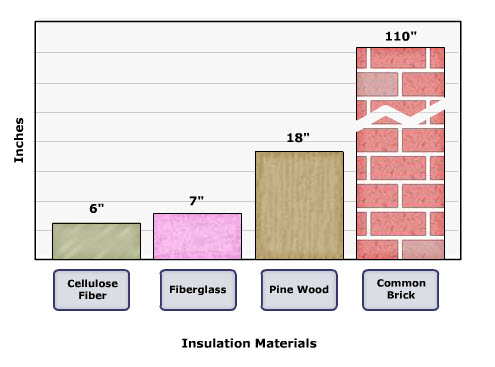
Types of Insulation
Look at the table below to learn about six types of insulation.
| Insulation | What is it made of? | What does it look like? | Additional Information |
|---|---|---|---|
Fiberglass
 |
Molten glass spun into microfibers | Pink or yellow in the form of batts or rolled blankets. | |
Rock Wool
 |
Rock | Gray or brown fibers in batts or blankets or as shredded loose-fill. | Manufactured in a similar way as fiberglass, but with molten rock instead of glass. |
Cellulose
 |
Recycled paper – newsprint or cardboard shredded into small bits of fiber. | Blown in as loose fill. | It is treated with fire- and insect-resistant chemicals. |
Rigid Foam
 |
Different types, but some made from post-consumer recycled content from fast food containers and cups. | Rigid sheets that are applied directly to framing. | Best where space is limited, but a high R-value is needed. Can be installed on the interior of a wall, but if installed inside, must be covered by a fire resistant material like wallboard. One drawback to foam is it deteriorates unless it is protected from prolonged exposure to sunlight and water. It is also more expensive than other insulation. |
Synthetic Insulation
 |
Usually polystyrene or polyurethane foam. | Polystyrene comes as rigid boards, and Polyurethane comes as rigid boards or sprayed in place systems. | Polystyrene is used for insulating basements, cathedral ceilings, or sidewalls. Polyurethane foams are high performance insulating materials. |
Composite Wall R-Values
Generally, walls are made up of several layers of different materials. The R-value of a composite wall is calculated by adding the effective R-values of each of the layers of the wall.
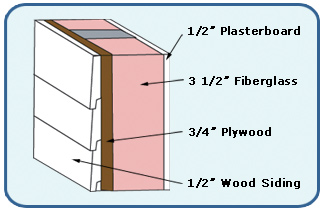
For example, the image below shows a wall made up of four layers—½ inch drywall inside for aesthetic purposes, real insulation in between the studs, ¾ inch plywood sheathing outside, and wood siding as the final exterior finish. Together, the layers of the wall are preventing heat loss.
We can calculate this wall’s composite R-value by adding the R-values of each layer.
Plasterboard (1/2 inch)
+ Fiberglass (3.5 inches @ 3.70 per inch)
+ Plywood (3/4 inches)
+ Wood Siding (1/2 inch)
-----------------------------------------
Total R-Value of Composite Wall
We can find the R-values for the walls by using the table from the page about R-Values [5] (the table is repeated below):
| Material | R-Value (ft2 o Fh / BTU) |
|---|---|
| Plain glass, 1/8 inch | 0.03 |
| Stone per inch | 0.08 |
| Common Brick per inch | 0.20 |
| Asphalt Roof Shingles | 0.44 |
| 1/2 inch Gypsum Board (Drywall or plasterboard) | 0.45 |
| Wood Siding, 1/2 inch | 0.81 |
| Plywood, 3/4 inch | 0.94 |
| Insulating sheathing, 3/4 inch | 2.06 |
| Fiberglass, per inch (battens) | 3.50 |
| Polystyrene per inch | 5.00 |
| Polyurethane Board per inch | 6.25 |
| Cinder Block (12 inches) | 1.89 |
Plasterboard (1/2 inch) = 0.4524
+ Fiberglass (3.5 inches @ 3.70 per inch) = 12.95
+ Plywood (3/4 inches) = 0.94
+ Wood Siding (1/2 inch) = 0.81
-----------------------------------------
Total R-Value of Composite Wall = 15.15
Examples
Example 1
A ceiling is insulated with 0.75" plywood, 2" of polystyrene board, and a 3" layer of fiberglass. What is the R-Value for the ceiling?
Solution:
The ceiling consists of three layers, and all three layers together prevent the heat loss. So, we need to add the R-values of all three layers
" of plywood has an R-value of 0.94
2" of polystyrene at 5.0 per inch will have an R-value of 10.00
3" of fiberglass at 3.7 per inch will have an R-value of 11.10
So the R-value of the ceiling is 22.04 ft2 oFh / BTU.
Example 2
Please watch the following 1:31 video presentation about Example #2. A wall consists of 0.5” wood siding (R = 0.81), 0.75” plywood (R = 0.94), 3.5” of fiberglass (R = 13.0), and 0.5” plasterboard (R = 0.45). What is the composite R-value of the wall?
Lesson 7b, Screen 7: Composite Wall R-Values
Example 10
This problem, we need to calculate composite R-value.
The wall consists of four layers. One half inch wood siding, and its R-value is given straight away for half inch as .81. And we have three-quarter inch plywood and this plywood’s R-value is also given as .94, this is for 3/4". Whereas the fiberglass, each inch has an R-value of 3.7. We are using 3 and a half inches. So, 3.5 times 3.7 would give us about 13.00 R-value. And the last layer would be one half inch plaster board which is also drywall and its R-value is given as .45.
1/2" wood siding: 0.81
3/4" plywood: 0.94
3 1/2 Fiberglass (3.7/inch): 13.00
1/2" plaster board: 0.45
Total: 15.2
So when you add these up you get 15.2 which means the composite R-value of this wall is 15.2 degrees F, foot squared, hour over BTUs.
Example 3
Please watch the following 1:18 video presentation about Example #3. What is the R-value of a wall that is made up of wood siding (R = 0.81), 5” of fiberglass (R = 3.70 per inch), and a layer of 0.5” drywall (R = 0.45)?
Lesson 7b, Screen 8: Composite Wall R-Values
Example 11
What is the R-value of a wall that is made up of wood siding (R= 0.81), 5” of fiberglass (R=3.70 per inch), and a layer of .5” drywall (R=0.45)?
Here we have, again a wall made up of three different layers. The first layer is wood siding which is outside, obviously, and its R-value is given as 0.81, whatever the thickness might be of that wood siding. And we have a second layer of fiberglass. And this fiberglass thickness is given as 5” and its R-value is given as 3.7 per inch. So we are using 5 inches so 5 times 3.7 would be 18.50. And we have a third layer of a drywall and this drywall has an R-value of 0.45, half inch drywall.
Wood siding: 0.81
5" fiberglass 3.7/inch: 18.50 (5x3.7)
Drywall: 0.45
Total R-value: 19.76
When you add all these three layers up, you get a total R-value of 19.76.
So the answer is 19.76 degrees F, foot squared, hour over BTUs. This is the composite R-value.
Example 4
Please watch the following 1:44 video presentation about Example #4. A wall is made up of 8” of stone, 3” of polyurethane board, and 0.75” of plywood. Calculate the composite R-value for the wall.
Lesson 7b, Screen 9: Composite Wall R-Values
Example 12
A wall is made up of 8” of stone, 3” of polyurethane board, and 0.75” of plywood. Calculate the composite R-value for the wall.
This is a problem where we have three layers for a wall and those three layers are made up of stone, polyurethane board and plywood. The first one is stone and its thickness is 8” and each inch of stone wall will provide an R-value of 0.08. Therefore, all these 8” together would provide 0.64. And the second layer is made up of 3” of polyurethane and each inch provides an R-value of 6.25, therefore, together, all 3” would provide an R-value of 18.75. The third layer is again three quarters inch plywood, and it provides an R-value of 0.94. So all these three together would have an R-value of 20.33 or the composite R-value is 20.33 degree F, foot squared, hour over BTUs.
8" stone (0.08/inch): 0.64
3" polyurethane (6.25/inch): 18.75
0.75" plywood: 0.94
Total: 20.33
Insulation Needs By Region
The United States map below shows insulation needs by region, as indicated by color and numbers.
Instructions: Click on the “zone” buttons below the map to see the U.S. Department of Energy’s Recommended Total R-Values for new construction of houses. Note that insulation R-values are different for the ceilings, walls, floor, etc.
U.S. Department of Energy recommended total R-Values for new construction houses, by regions and by various parts of the house.
Insulation Needs by Region
The U.S. Department of Energy released recommended total R-values for new construction houses. The info is based on regional zone and covers various parts of the house. The states within each zone are listed below, followed by a data table containing the R-values for each part of the house. The R-values are dependent on the type of heating system being used and may vary for each. Some states may lie in multiple zones.
Zone 1
States:
- Florida
| Zone 1 | Gas Heat Pump Fuel Oil |
Electric Furnace |
|---|---|---|
| Attic | R-49 | R-49 |
| Cathedral Ceiling | R-38 | R-60 |
| Wall | R-18 | R-28 |
| Floor | R-25 | R-25 |
| Crawl Space | R-19 | R-19 |
| Slab Edge | R-8 | R-8 |
| Basement Interior | R-11 | R-19 |
| Basement Exterior | R-10 | R-15 |
Zone 2
States:
- California
- Arizona
- Texas
- Louisiana
- Mississippi
- Alabama
- Florida
- Georgis
| Zone 2 | Gas Heat Pump Fuel Oil |
Electric Furnace |
|---|---|---|
| Attic | R-49 | R-49 |
| Cathedral Ceiling | R-38 | R-38 |
| Wall | R-18 | R-22 |
| Floor | R-25 | R-25 |
| Crawl Space | R-19 | R-19 |
| Slab Edge | R-8 | R-8 |
| Basement Interior | R-11 | R-19 |
| Basement Exterior | R-10 | R-15 |
Zone 3
States:
- North Carolina
- South Carolina
- Georgia
- Alabama
- Mississippi
- Tennessee
- Louisiana
- Arkansas
- Oklahoma
- Texas
- New Mexico
- Arizona
- Utah
- New Mexico
- Nevada
- California
- Alaska
| Zone 3 | Gas Heat Pump Fuel Oil Electric Furnace |
|---|---|
| Attic | R-49 |
| Cathedral Ceiling | R-38 |
| Wall | R-18 |
| Floor | R-25 |
| Crawl Space | R-19 |
| Slab Edge | R-8 |
| Basement Interior | R-11 |
| Basement Exterior | R-10 |
Zone 4
States:
- New York
- New Jersey
- Maryland
- Delaware
- Virginia
- Pennsylvania
- West Virginia
- Ohio
- Indiana
- Illinois
- Kentucky
- Tennessee
- North Carolina
- Georgia
- Arkansas
- Missouri
- Kansas
- Oklahoma
- Colorado
- Texas
- New Mexico
- Arizona
- California
- Oregon
- Washington
| Zone 4 | Gas Heat Pump Fuel Oil |
Electric Furnace |
|---|---|---|
| Attic | R-38 | R-49 |
| Cathedral Ceiling | R-38 | R-38 |
| Wall | R-13 | R-18 |
| Floor | R-13 | R-25 |
| Crawl Space | R-19 | R-19 |
| Slab Edge | R-4 | R-8 |
| Basement Interior | R-11 | R-11 |
| Basement Exterior | R-4 | R-10 |
Zone 5
States:
- Washington
- Oregon
- Idaho
- California
- Nevada
- Utah
- Colorado
- Arizona
- New Mexico
- Wyoming
- South Dakota
- Nebraska
- Kansas
- Iowa
- Missouri
- Illinois
- Michigan
- Indiana
- Ohio
- Pennsylvania
- New York
- West Virginia
- Maryland
- New Jersey
- New Hampshire
- Massachusetts
- Rhode Island
- Connecticut
| Zone 5 | Gas | Heat Pump Fuel Oil |
Electric Furnace |
|---|---|---|---|
| Attic | R-38 | R-38 | R-49 |
| Cathedral Ceiling | R-30 | R-38 | R-38 |
| Wall | R-13 | R-13 | R-18 |
| Floor | R-11 | R-13 | R-25 |
| Crawl Space | R-13 | R-19 | R-19 |
| Slab Edge | R-4 | R-4 | R-8 |
| Basement Interior | R-11 | R-11 | R-11 |
| Basement Exterior | R-4 | R-4 | R-10 |
Zone 6
States:
- California
- Washington
- Idaho
- Wyoming
- Montana
- Utah
- Colorado
- North Dakota
- South Dakota
- Minnesota
- Iowa
- Wisconsin
- Michigan
- New York
- Pennsylvania
- Vermont
- New Hampshire
- Maine
| Zone 6 | Gas | Heat Pump Fuel Oil |
Electric Furnace |
|---|---|---|---|
| Attic | R-22 | R-38 | R-49 |
| Cathedral Ceiling | R-22 | R-30 | R-38 |
| Wall | R-11 | R-13 | R-18 |
| Floor | R-11 | R-11 | R-25 |
| Crawl Space | R-11 | R-13 | R-19 |
| Slab Edge | (c) | R-4 | R-8 |
| Basement Interior | R-11 | R-11 | R-11 |
| Basement Exterior | R-4 | R-4 | R-10 |
Calculating Wall Heat Loss
Heat loss from the surface of a wall can be calculated by using any one of the three formulas we have covered in Part A of this Lesson.
Equations
The heat loss in an hour equation
The heat loss in a day equation
The heat loss in full heating season
The heat loss from walls, windows, roof, and flooring should be calculated separately, because of different R-Values for each of these surfaces. If the R-value of walls and the roof is the same, the sum of the areas of the walls and the roof can be used with a single R-value.
Example
A house in Denver, CO has 580 ft2 of windows (R = 1), 1920 ft2 of walls and 2750 ft2 of roof (R = 22). The walls are made up of wood siding (R = 0.81), 0.75” plywood, 3.5” of fiberglass insulation, 1.0” of polyurethane board, and 0.5” gypsum board. Calculate the heating requirement for the house for the heating season, given that the HDD for Denver is 6,100.
Solution:
Heating requirement of the house = Heat loss from the house in the whole year. To calculate the heat loss from the whole house, we need to calculate the heat loss from the walls, windows, and roof separately, and add all the heat losses.
Heat loss from the walls:
Area of the walls = 1,920 ft2, HDD = 6,100, and the composite R- value of the wall needs to be calculated.
| Material | R-Value |
|---|---|
| Wood Siding | 0.81 |
| 3/4 inch plywood | 0.94 |
| 3.5 inches of fiberglass 3.5 in x 3.7 / in | 12.95 |
| 1.0 inch of polyurethane board = 1.0 in x 5.25 / in | 5.25 |
| 1/2 inch Gypsum board | 0.45 |
| Total R-Value of the walls | 20.40 |
Total heat loss from the house = 13.78 + 84.91 + 18.30 =116.99 MMBTU in a year or heating requirement is 116.99 million BTUs per year.
Calculating Wall Heat Loss Example Problems
Example #1
Please watch the following 4:58 presentation about Example #1. A house in State College, PA has 580 ft2 of windows (R = 1), 1920 ft2 of walls, and 2750 ft2 of roof (R = 22). The walls are made up of wood siding (R = 0.81), 0.75” plywood, 3” of fiberglass insulation, 1.5” of polyurethane board, and 0.5” gypsum board. Calculate the heating requirement for the house for the heating season.
Lesson 7b, Screen 14: Calculation of Wall Heat Loss
Example 15 (formerly Example 3-14)
A house in State College, PA has 580 ft2 of windows (R=1), 1920 ft2 of walls, and 2750 ft2 of roof (R=22). The walls are made up of wood siding (R=0.81), 0.75” plywood, 3” of fiberglass insulation, 1.5” of polyurethane board, and 0.5” gypsum board. Calculate the heating requirement for the house for the heating season.
Here in this problem, we are trying to calculate the heat loss from the entire house. Heat loss through windows, heat loss through roof, heat loss through walls and add them up. We can directly calculate heat loss through windows. Area is given as 580 ft2, R-value is given as 1 and HDD for State College is 6000 degree F days (°F days). So heat loss for the season is equal to 580 ft2 times 6000 °F days times 24 hours in a day divided by 1 R-value (ft2 (°F hour/BTU). So we can cancel these and the heat loss through windows is 83,520,000 BTUs.
Windows
Similarly, we can calculate heat loss through the roof. And area of the roof is given as 2750 ft2 times 6000 °F days times 24 hours over a day divided by 22 ft2 °F hour over BTU. Now, when you do this calculation, we lose about 18 million BTUs through the roof.
Heat Loss Season
Heat Loss Roof
For the wall heat loss, we need to calculate the composite R-value because we are not given the R-value straight away, and we are given the area. So, let’s calculate the composite R-value. The first layer is wood siding, and wood siding is 0.81 in R- value and the next layer is ¾” plywood and whose R-value is 0.94. And we got 3” of fiberglass and each inch provides an R-value of 3.7 therefore 3” would be 11.10, and we have another 1 ½ of polyurethane which has 6.25 per inch R-value therefore 1.5” would provide an R-value of 9.375. At the end or inside, we have ½” drywall whose R-value is 0.45. So together, all these layers would provide an R-value of 22.7.
Wood siding = 0.81
¾ “ plywood = 0.94
3” fiberglass = 11.10
1.5” polyurethane = 9.375
.5” dry wall = 0.45
Total = 22.7
So, heat loss now can be calculated. We know the area that is 1920 ft2 given and same 6000 °F days times 24 hours per day divided by 22.67 and this comes out to be 12,119,164 BTUs.
So when you add all these three heat losses, the total heat loss is equal to 113,753,164 BTUs per heating season.
Example #2
Please watch the following 9:00 presentation about Example #2. A single-story house in Anchorage, AK (HDD = 11,000) is 50 ft by 70 ft with an 8 ft high ceiling. There are six windows (R = 1) of identical size, 4 ft wide by 6 ft high. The roof is insulated to R-30. The walls consist of a layer of wood siding (R = 0.81), 2” of polyurethane board (R = 6.25 per inch), 4” of fiberglass (R = 3.70 per inch), and a layer of drywall (R = 0.45). Calculate the heat loss through the house (not counting the floor) for the season. (A good estimate for the area of the roof is 1.1 times the area of the walls, before you subtract out the area for the windows.)
Wall Heat Loss #3
Problem
[ON SCREEN TEXT]: A single-story house in Anchorage, AK (HDD = 11,000) is 50 ft by 70 ft with an 8 ft high ceiling. There are six windows (R = 1) of identical size, 4 ft wide by 6 ft high. The roof is insulated to R-30. The walls consist of a layer of wood siding (R = 0.81), 2” of polyurethane board (R = 6.25 per inch), 4” of fiberglass (R = 3.70 per inch), and a layer of drywall (R = 0.45). Calculate the heat loss through the house (not counting the floor) for the season. (A good estimate for the area of the roof is 1.1 times the area of the walls, before you subtract out the area for the windows.)
SARMA PISUPATI: OK, for this problem, 3.15. We do, more or less, the same thing as the last house, except this house is in Anchorage, Alaska, where HDD happens to be 11,000 degree days. OK. Now we have to calculate here, heat loss through windows, through walls, and through roof, to calculate the total heat loss from the house, the same way that we have done before.
Heat loss through windows. We need the area of the windows first. So area of windows equal to-- Each window is 4 feet by 6 feet. So this is 24 square feet. So we have six of them, so the total area is 144 square feet. So heat loss equal to 144 feet square times HDDs 11,000 degree days times 24 hours in a day, and divided by r value, r value happens to be 1. So 1 feet square, degrees Fahrenheit, hour over BTU.
So you could cancel out some of these. We'll get BTUs heat loss. This is in a year. OK. So we would get this one to be approximately 38 million. 38,016,000 BTUs. This is per season or per year. OK. Now the second thing that we have to do is walls.
Here we have to calculate the area and also the r value. r value because it is a composite wall consisting of four layers. It has wood siding, which has an r value of 0.81 and 2 inches of polyurethane. And 2 times 6.25, so that is 12.5 r value. And we have a third layer, 4 inches of fiberglass. 4 inches times 3.7, that's equal to 14.8.
And then we also have 1/2 inch drywall. And we know that the drywall r value is straight away 0.45, so now the total r value of this wall happens to be 28.56. OK. Now we have to calculate the area of the walls. Area of the walls we can calculate.
Let me draw a little picture here and show you. If we have-- Let's say this is the area, and we have-- and this side is about 70, this side is 50. And we will have under there, 50 this side, and 70 this side. So total times this height is 8 feet. So the total area would be 2 times 120. 120 is 70 plus 50 times 2, because twice these values, times 8 feet is the height. So we get about 1,920 feet square.
Of course, this also has some windows, about six windows as we originally looked at, but at this point, we will take this as 1920 and subtracting windows from this. Windows is 144 feet square, so 1920 minus 144, would give us 1776 feet square.
OK, so now we have to calculate the area of-- Now, if we calculate the area of 1776 feet square times 11,000 times, this is degrees Fahrenheit days, times 24 hours per day, divided by-- we have 28.56. So the heat loss, in here, comes out to be 16,416,806 BTUs per year.
OK, now we have to calculate roof. Roof happens to be 1.1 times the area of the walls. Area of the walls was 1920 feet square. Again, we have to take this without the windows, actual area of the walls, times 1.1, that happens to be 2112 feet square.
So heat loss 2112 feet square times 11,000 times 24, divided by-- r value of this is 30-- degrees Fahrenheit, feet square, hour, over BTU. So this comes out to be 18,585,600 BTUs per year.
So the total heat loss now, would be the addition of all these three together. So that is, first we have, how much? If we look at, we have 38,016,000, so 38,016,000 plus 16,416,806 plus 18,585,600, so that is equal to 73, 019,000 BTUs. So that is the total heat loss from the house.
Fuel Choices
Various fuels such as natural gas, electricity, fuel oil, and so on, are used to heat a house. Click on the graph below to see the percent of households that use each type of heating fuel.
| Fuel Type | Percentage used |
|---|---|
| Natural Gas | 49% |
| Electricity | 34% |
| Fuel Oil / LPG | 11% |
| Other | 6% |
As you see, about 50 percent of the households in the United States use natural gas as their main heating fuel, and about 35 percent of the households use electricity to heat their homes. Another 11% use fuel oil, and the last 6% use something other than natural gas, electricity, and fuel oil.
Capacity and Consumption
Capacity
The amount of heat a furnace can deliver is called its capacity. Heating units are manufactured and sold by their capacity. The heating capacities of Natural Gas, Propane and Fuel Oil are measured according to BTU/h, and the capacity of Electricity is measured in kilowatts.
Consumption
The amount of energy a furnace actually uses is called consumption. In other words, we pay monthly bills for the consumption of a particular heating fuel. Heating Fuels are sold to consumers in different units of measure. For example, Natural gas is sold by cubic feet (ft3).
Press play to see the difference between capacity and consumption in a gas-heated home. (36 seconds)
The animation shows the capacity of the gas heater in BTUs per hour and a meter showing the consumption of fuel in cubic feet.
Fuel Comparison
| Fuel | Capacity | Consumption | Additional Information |
|---|---|---|---|
| Natural Gas | Measured in British thermal units per hour (BTU/h). Most heating appliances for home use have heating capacities of between 40,000 and 150,000 BTU/h. In the past, gas furnaces were often rated only on heat input; today the heat output is given. | Consumption of natural gas is measured in cubic feet (ft3). This is the amount that the gas meter registers and the amount that the gas utility records when a reading is taken. One cubic foot of natural gas contains about 1,000 BTU of energy. | Utility companies often bill customers for CCF (100 cu. ft) or therms of gas used: one therm equals 100,000 BTUs. Some companies also use a unit of MCF, which is equal to 1,000 cu. ft One MCF equals 1,000,000 BTUs (1 MM BTUs). |
| Propane or Liquefied Petroleum Gas (LPG) | Measured according to BTU/h. | Consumption of propane is usually measured in gallons; propane has an energy content of about 91.300 BTUs per gallon. | Can be used in many of the same types of equipment as natural gas. It is stored as a liquid in a tank at the house, so it can be used anywhere, even in areas where natural gas hookups are not available. |
| Fuel Oil | The heating (bonnet) capacity of oil heating appliances is the steady-state heat output of the furnace, measured in BTU/h. Typical oil-fired central heating appliances sold for home use today have heating capacities of between 56,000 and 150,000 BTU/h. | Oil use is generally billed by the gallon. One gallon of #2 fuel oil contains about 140,000 BTU of potential heat energy. | Several grades of fuel oil are produced by the petroleum industry, but only #2 fuel oil is commonly used for home heating. |
| Electricity | The heating capacity of electric systems is usually expressed in kilowatts (kW); 1 kW equals 1,000 W. A kilowatt-hour (kWh) is the amount of electrical energy supplied by 1 kW of power over a 1-hour period. Electric systems come in a wide range of capacities, generally from 10 kW to 50 kW. | Electricity is sold in kWh (kilowatts per hour). | The watt (W) is the basic unit of measurement of electric power. |
Heating Values of various fuels
Each unit of fuel when burned gives different amounts of energy. The energy that is released when a unit amount of fuel is burned is called the heating value. The heating value of a fuel is determined under a standard set of conditions. A comparison of approximate heating values of various fuels is shown in the table below.
| Fuel | Unit | Heating Value (BTU's) |
|---|---|---|
| Natural Gas | CCF (100 Cu. ft) or Therm | 100,000 |
| Natural Gas | MCF (1,000 Cu.ft) | 1,000,000 |
| Fuel Oil | Gallon | 140,000 |
| Electricity | kWh | 3,412 |
| Propane | Gallon | 91,300 |
| Bituminous Coal | Ton | 23,000,000 |
| Anthracite Coal | Ton | 26,000,000 |
| Hardwood | Cord | 24,000,000 |

Heating Efficiency
An assumption is made here that all the energy from the fuel is released, and all the heat is available to heat the place. However, generally, when a fuel is burned in a furnace, not all the energy (heat) is available for the final end user.
The energy efficiency of a furnace is not 100 percent. Not all the energy from the fuel is released, and not all the heat is available to heat the place. For example, if a furnace’s efficiency is, say, 50 percent, then twice as much fuel would be needed to heat a home.
Looking again at the table on the previous screen, we saw that the heating value of fuel oil is given as 140,000 BTUs. However, if the furnace’s efficiency is 50 percent, then the actual heating value of fuel oil is 140,000 BTUs x 0.5 (efficiency) = 70,000 BTUs. In other words, when a gallon of oil is burned, 70,000 BTUs of heat is actually available to the user.
| Fuel | Unit | Heating Value (BTU's) | If Efficiency = 50 % |
|---|---|---|---|
| Natural Gas | CCF (100 Cu. ft) or Therm | 100,000 | 50,000 |
| Natural Gas | MCF (1,000 Cu.ft) | 1,000,000 | 500,000 |
| Fuel Oil | Gallon | 140,000 | 70,000 |
| Electricity | kWh | 3,412 | 1706 |
| Propane | Gallon | 91,300 | 45,650 |
| Bituminous Coal | Ton | 23,000,000 | 11,500,000 |
| Anthracite Coal | Ton | 26,000,000 | 13,000,000 |
| Hardwood | Cord | 24,000,000 | 12,000,000 |
Efficiency of a Furnace
The table below contains the data from a line plot showing the efficiency of a furnace. The percent efficiency is dependent on the heating value of fuel oil (measured in BTU) and shows a strong positive correlation.
| Efficiency of a Furnace | Heating Value of Fuel Oil (BTUs) |
|---|---|
| 50% | 70000 |
| 55% | 77000 |
| 60% | 84000 |
| 65% | 90000 |
| 70% | 100000 |
| 75% | 105000 |
| 80% | 111000 |
| 85% | 122000 |
| 90% | 125000 |
| 95% | 131000 |
| 100% | 140000 |
It can be clearly seen that as the efficiency of the furnace increases, the amount of heat available increases proportionally.
The higher the efficiency, the less oil needs to be put into the furnace to get the same amount of heat output.
Most of the heating furnaces burn fuel and release hot combustion gases. The hot combustion gases heat the incoming cold air and go out through the chimney. In older furnaces, all the heat in the fuel is not released or not transferred to the cold air (or water, in the case of heat registers and water heaters), and therefore is lost through the chimney. The air or water that is heated distributes the heat throughout the house. Newer models of furnaces have gotten better at getting more of the heat into the cold air and, therefore, into your house.
Click the play button and observe how a wood burning furnace operates at 75% efficiency.
Click here to open a text description of How a Wood Furnace Operates
How a Wood Burning Furnace Operates
Cold combustion air from outside is pulled into the furnace combustion chamber by an electric blower. The wood fire in the chamber heats the air to 1 million BTUs. The hot combustion gasses heat the cold, outside air to 750,000 BTUs, which will circulate through the house. The combustion gasses (250,000 BTUs) travel out through the chimney.
Furnaces are usually not as efficient when they are first firing up as they are running at steady-state. It is sort of like a car getting better mileage in steady highway driving than in stop-and-go city traffic.
What matters over the course of the year is the total useful heat the furnace delivers to your house versus the heat value of the fuel it consumes. This is kind of like measuring the gas mileage your car gets by asking how many miles you drove this year and dividing it by how many gallons of gas you bought.
For furnaces, they call this measure the AFUE (Annual Fuel Utilization Efficiency). The federal minimum-efficiency standards for furnaces and boilers took effect in 1992, requiring that new furnace units have an AFUE of at least 78 percent and new boiler units have an AFUE of at least 80 percent. In comparison, many old furnaces and boilers have AFUE ratings of only 55 to 65 percent.

To find out how efficient your furnace is, look for an energy guide label like this:
The table below gives the efficiencies of most efficient furnaces that were available in 2002–2003.
| Fuel | Furnace Type | Efficiencies (%) |
|---|---|---|
| Natural Gas | Hot air | 93.0 - 96.6 |
| Natural Gas | Hot Water | 83.0 - 95.0 |
| Natural Gas | Steam | 81.0 - 82.7 |
| Fuel Oil | Furnace | 83.8 - 86.3 |
| Fuel Oil | Hot Water | 86.0 - 87.6 |
| Fuel Oil | Steam | 82.5 - 86.0 |
When buying a new furnace, make sure its heating capacity (output) is appropriate for your home. If the insulation and/or windows in your home have been upgraded since the old heating equipment was installed, you can probably use a much less powerful furnace or boiler. Oversized furnaces operate less efficiently because they cycle on and off more frequently; in addition, larger furnaces are more expensive to buy.
Energy Costs
It is clear now that when a unit of fuel is burned not all of it is available to the end user, and that as the furnace efficiency increases, higher amounts of heat will be available. An important question that needs to be addressed is how much it costs to buy the energy or heat to heat a place.
Fuel is usually sold in gallons or CCF or kWh. Comparing the actual cost of energy to produce a certain amount of heat for the end user would be easy if the comparison is made on an energy basis rather than on a unit basis. That is, \$/BTUs rather than \$/gal or CCF or kWh.
We can use the following formula to calculate Actual Energy Cost:
Example
Let’s say we need one million BTUs to keep a place warm at a certain temperature. What would it cost to get those million BTUs from oil or gas or electricity? Let’s assume that:
| Material | Cost per unit | Efficiency | Heating Value |
|---|---|---|---|
| Natural Gas | $6.60/MCF | 90% | 1,000,000 BTUs or 1.0 MM BTU/MCF |
| Oil | $1.25/Gallon | 85% | 140,000 BTUs or 0.14 MM BTUs/Gallon |
| Electricity | $0.082/kWh | 97% | 3,412 BTUs or .003412 MM BTUs/kWh |
Using the formula below, we can calculate the Actual Energy Cost.
Energy Cost Examples
Example 1
Please watch the following 1:26 presentation about Example #1. Your old oil furnace runs at about 68% efficiency. If you buy your oil for $1.02/gal, calculate your actual cost on an MM BTU basis.
Click here to open a transcript of the Energy Cost Example #1
Energy Cost Example #1
Your old oil furnace runs at about 68% efficiency. If you buy your oil for $1.02/gal, calculate your actual cost on an MM BTU basis.
Ok, the old furnace runs at about 68% efficiency in this problem. This is 5.6 and the old furnace runs at an efficiency of E=0.68, and we have the actual cost per unit price or unit fuel which is $1.02 per gallon. And we also know the calorific value or heating value in millions of BTUs. When you burn one gallon of oil, we get .13 million BTUs so we apply the same formula to get the actual cost. Which is cost per unit fuel which is $1.02/gallon divided by the heating value which is 0.13 MMBTUs per gallon. We have to have the same units here. And times the efficiency here. Efficiency is 0.68. Gallons and Gallons are canceled, and we get this one as $11.50 / Million BTUs.
Example 2
Please watch the following 2:44 presentation about Example #2. Natural gas costs 9.74 dollars/MCF. Heating oil costs 0.99 cents/gal. The natural gas furnace runs at 90% efficiency and the oil furnace runs at 80% efficiency. Which fuel is cheaper?
Click here to open a transcript of the Energy Cost Example #2
Energy Cost Example #2
Natural gas costs $9.74/MCF. Heating oil costs $0.99/gal. The natural gas furnace runs at 90% efficiency and the oil furnace runs at 80% efficiency. Which fuel is cheaper?
Ok. This 5.7 is an interesting problem here. We are trying to compare the prices of two fuels – Natural Gas which sells for $9.74/MCF, and we also have oil that sells at $0.99/gallon. We are trying to compare the prices of these two and choose which one is the best fuel or cheapest fuel. So we need to calculate the price per million BTUs so that we can compare these two fuels. And we also know the furnace efficiencies of each of these. Natural gas furnace efficiency is 0.9, and we know the oil furnace efficiency is 0.8; it is given. So we need to calculate the actual cost and compare the cost.
Natural gas actual cost will be cost per unit fuel, which is $9.74/MCF divided by the heating value per unit fuel. Heating value for this one happens to be 1.0 Million BTUs per MCF, and we have to multiply by the efficiency here in the denominator which is 0.9, so the Natural Gas price turns out to be $10.83 or $10.83 per Million BTUs (MMBTUs).
When you do similar calculation for oil here, the actual price is, per unit is $0.99 per gallon here and how many million BTUs do we get per gallon? 0.13 Million BTUs (0.13 MMBTUs). We have done this before. We have to have the same units here. Gallons and gallons and MCF and MCF here in this case (natural gas) and times the efficiency is 0.8. So the price works out to be $9.50 per Million BTUs. Same million BTUs would cost $10.82 for Natural Gas and oil would be $9.50, so oil is cheaper.
Annual Heating Costs
In the example on the page 12, we see that the heat loss from the house (walls, windows, and the roof) was 116.53 MM BTUs. We also know that it costs $24.77 for 1MM BTUs if electrical resistance heating is used (see Example 17 on page 26). The total cost for the heating can be calculated as follows:
The price of fuel oil is $10.50 per MMBtu. The annual heating cost would be:
Example
A house in International Falls, MN (HDD = 10,500) consists of 1248 ft2 of walls with an R-value of 13 and 1150 ft2 of roof with an R value of 29. The home is heated with natural gas. The AFUE is 0.90 and the price of natural gas is $0.88/CCF. What is the annual heating cost?
Energy cost per million BTUs from natural gas can be calculated using the following equation.
Heat required can be calculated from the heat loss. Heat loss from the house is from two sources: walls and the roof. Heat loss from each of these sources for a year (season) can be calculated by using the following equation.
Total heat loss = sum of heat loss from the walls and the roof
Annual heating cost = Annual heat loss (MMBTUs) x Actual energy cost ($/MMBTU)
Annual Heating Cost Examples
Example 1
Please watch the following 6:01 presentation about Example Problem #1. A house in Bismark, ND (HDD = 9,000) has 860 ft2 of windows (R = 1), 2,920 ft2 of walls (R = 19), and 3,850 ft2 of roof (R = 22). Calculate how much heating oil is required to heat this house for the heating season. The furnace efficiency is 80%.
Click here to open a text description of the Annual Heating Cost Example 1.
Annual Heating Cost Example 1
A house in Bismark, ND (HDD = 9000) has 860 ft2 of windows (R = 1), 2920 ft2 of walls (R = 19), and 3850 ft2 of roof (R = 22). Calculate how much heating oil is required to heat this house for the heating season. The furnace efficiency is 80%.
Ok, this problem is very similar to what we have done before. Which is calculating the heat loss from various surfaces and adding all of those to get the total heat loss from the house. And to calculate the oil requirement based on the furnace efficiency. The house is located in Bismark, ND and HDD there is given as 9,000, so HDD is given. This HDD remains the same for all different surfaces. And we also know the surfaces of each of these components, like windows. Let’s do the calculation first for windows.
Windows area is given as 860 square ft, and we also know the R-value of this. R-value is given as 1 – this is ft °F h/BTUs. So we can calculate heat loss through windows. Where all we need is the area, 860 square ft times HDD which is 9,000 in this case times 24 hours in a day divided by, we get the R-value here. That is 1 ft°F h/BTU. So ft/ ft cancel, °F/°F, 24 hours/24 hours, days and days, so the total heat loss through windows is the number that we get here. It happens to be 185,760,000 BTUs.
Similarly, we can calculate the heat loss - this is through windows. We can calculate heat loss through the walls. Wall area is 2,920 ft2 times 9,000 °F days times 24 hours per day divided by R-value of 19 for walls. And we can cancel out the units and make sure that everything makes sense and this turns out to be 33,195,789 BTUs.
Now heat loss through the roof. You can calculate it again separately and the area of the roof happens to be 3850 ft2, and 9,000 degree days times 24 hours over a day divided by, the roof generally has higher R-value, 22 ft2 °F h/BTUs, ok? Now let’s cancel out these units and the heat loss is to be 37,800,000 BTUs. So the total heat loss is the sum of all these three and when you add these up you get 256,755,789 BTUs.
Now, the furnace efficiency is given, and we are using, in this case, heating oil. Heating oil is 130,000 BTUs so how much is required? How much heating oil is required? We need 256,755,789 BTUs. When we buy heating oil, we get 130,000 BTUs per every gallon, and although we get 130,000, this is theoretical, the efficiency is given as 0.8 so only 80% will get really available as heat. So, that makes it, actually, the requirement a little bit higher, so that is equal to now, if we do this calculation, it will be 2,468.8 gallons or roughly 2,469 gallons of oil is required to heat this place.
Pay Back Period
Earlier sections illustrated that adding more insulation and improving the R-value of a wall would help in cutting heat loss. Less heat loss reduces the amount of fuel that needs to be burned, thereby reducing the heating costs and protecting the environment. However, adding insulation often involves additional investment.
The money invested into insulation can be recovered or paid back using the money saved because of the reduction of fuel usage. The time it takes to recover the additional cost through savings is called the pay-back period. A simple pay back is the initial investment divided by annual savings after taxes.
A simple calculation illustrates this term. If the R-value of the wall used in an earlier example is improved to R-23 by adding additional insulation, which costs $254, the heat loss can be reduced. The new heat loss after improvement can be calculated using the equation below.
Heat loss from the roof remains the same and is equal to 9.99 MM BTUs. Therefore, new annual total heat loss is only 13.7 + 9.99 =23.69 MM BTUs. The annual cost of heating after this improvement would be:
The savings is $334.96 - $232.16 = $102.80 every year. Remember that to get this savings, an investment of $254 was made. So if this investment was paid off by the savings, it would take
The pay-back period is 2.47 years. Shorter pay-back periods indicate that the additional investment can be paid off quickly and the homeowner can start saving money after that.
The formula below will help you to estimate the cost effectiveness of adding insulation in terms of the "years to payback" for savings in heating costs.
Where:
Ci = Cost of insulation in $/square feet. Collect insulation cost information; include labor, equipment, and vapor barrier if needed.
Ce = Cost of energy, expressed in $/BTUs. To calculate this, divide the actual price you pay per gallon of oil, kilowatt-hour (kWh) of electricity, gallon of propane, or therm (or per one hundred cubic feet [CCF]) of natural gas by the BTU content per unit of fuel.
E = Efficiency of the heating system. For gas, propane, and fuel oil systems, this is the Annual Fuel Utilization Efficiency, or AFUE.
R1 = Initial R-value of section
R2 = Final R-value of section
R2 – R1 = R-value of additional insulation being considered
HDD = Heating degree days/year. This information can usually be obtained from your local weather station, utility, or oil dealer.
24 = Multiplier used to convert HDD to heating hours (24 hours/day).
The formula above works only for uniform sections of the home. For example, you can estimate years to pay back for a wall or several walls that have the same R-values, if you add the same amount of insulation everywhere. Ceilings, walls, or sections of walls with different R-values must be figured separately.
Example
Mr. Energy Conscious (who lives in East Lansing, MI with an HDD of 7,164) wants to know how many years it will take to recover the cost of installing additional insulation in his attic. He renovated his attic and increased the level of insulation from R-19 to R-30 by adding additional insulation. He has a gas furnace with an AFUE of 0.88 and pays $0.95/CCF for natural gas. The attic insulation costs $340 to cover 1,100 sq. ft.
The pay-back period is given by the equation 5.5:
R1 = 19; R2 = 30; and R2 - R1 = 30 - 19 = 11
HDD = 7,164 and E = 0.88
The most important part of this problem is to determine the cost of insulation per one sq. ft (Ci) and cost of energy per one BTU (Ce).
Note: The cost for one BTU is a very small number.
Substituting the values in the equation,
After 8.65 years, Mr. Energy Conscious can start saving money for himself for the rest of the period that he lives in that home. During the entire period the energy that he is not using can help the environment.
Pay Back Period Examples
Example 1
Please watch the following 3:04 presentation about Example Problem #1. For a house in Hackensack, NJ (HDD = 4,600), the installed cost to upgrade from R-13 to R-22 is $0.60/ft2. The AFUE for the oil furnace is 0.78 and heating oil costs $1.13/gal. How long will it take to recover the initial investment?
Click here to open a transcript of the Payback Period Example Problem #1.
Payback Period Example 1
For a house in Hackensack, NJ (HDD = 4,600), the installed cost to upgrade from R-13 to R-22 is $0.60/ft2. The AFUE for the oil furnace is 0.78 and heating oil costs $1.13/gal. How long will it take to recover the initial investment?
Ok, this is 5.10. Heating Degree Days are given. In this problem, basically we are trying to calculate the pay back period again using the formula that we have. That we derived basically and payback period for adding insulation is cost of insulation times R1 times R2 times efficiency divided by cost of energy times the difference in R-value times HDD times 24. That is the formula that we need to use.
We have all the data. HDD is given as 4,600 and cost of insulation Ci is given as $0.60 per ft2 and the efficiency of the furnace is given as 78% or 0.78. We know the initial R-value, R1 = 13, and we know the final R-value; the improved R-value which is 22, the difference is 9. And we know the price of energy or cost of energy. We are paying $1.13 to buy a gallon of oil and when we buy a gallon of oil by paying $1.13 we get 130,000 BTUs.
So, for every BTU we pay $0.0000869. So we can use the formula now. It consists of Ci, Ci is cost of insulation, which is 0.06 per ft2, dollars per ft2 times R1 which is 13, again units, you have to make sure ft2, °F, hr/BTU. And here R2 is 22 and times the efficiency which is .78 divided by the cost of energy which is dollars per BTUs. $0.0000869/1 single BTU times the difference between these two R values here and that is 22 minus 13 (9) times days, (HDD) 4,600 times 24 and when you do this calculation it turns out to be 15.5 years is the payback period.
Example 2
Please watch the following 4:10 presentation about Example Problem #2. Lt. Dave Rajakovich has 1200 ft2 of roof in his home in Pittsburgh, PA (HDD = 6,000). He is considering upgrading the insulation from R-16 to R-22. The estimate from the contractor was $775. His home is heated with natural gas. Last year, the average price he paid for natural gas was $9.86/MCF. Assuming an AFUE of 86%, how long will it take Dave to recover his investment?
Click here to open a text description of the Payback Period Example Problem #2.
Payback Period Example #2
Lt. Dave Rajakovich has 1200 ft2 of roof in his home in Pittsburgh, PA (HDD = 6,000). He is considering upgrading the insulation from R-16 to R-22. The estimate from the contractor was $775. His home is heated with natural gas. Last year, the average price he paid for natural gas was $9.86/MCF. Assuming an AFUE of 86%, how long will it take Dave to recover his investment?
Ok, this is 5.11. Here Dave has a house, and he is trying to improve the insulation and the contractor comes up with an estimate of $775. He is using natural gas to heat the home, and we are trying to calculate how long will it take Dave to recover his investment? And this is a typical problem that uses an equation for payback period. Equal to Ci, cost of insulation, times R1 times R2 times efficiency divided by cost of energy times again R2 minus R1, this is the final R-value minus the initial R-value times HDD times 24.
Do we have all the pieces of information for this formula?
Cost of insulation: Cost of insulation should be in dollars per square foot. So Dave has got an estimate of $775 to cover an area of 1200 square foot. Roof area happens to be 1200 ft2. To cover this area with insulation it costs $775, so we can calculate the cost per ft. This happens to be $0.65 per ft2. That’s what we want, per ft2.
Do we know R1? Yes we know, R1 is equal to 16, R2 is equal to 22 and the furnace efficiency, E, is equal to 0.86. And we also know HDD. HDD is 6,000, and we know 24 hours.
Only thing here is we need to calculate the cost, Ce, cost of energy. And we are paying here, or Dave is paying $9.86 per MCF. Remember, MCF is basically one million BTUs. So the price would be $9.86 per million BTUs. So this will be equal to 0.00000986.
And if we plug this into this number here, into this formula here, 0.65 times 16 times 22 times 0.86 and divided by this is 0.00000986 and R2 – R1 happens to be 6 and 6,000 is the degree days and 24. This should come out to be, I guess 23 years roughly. This is kind of a long time period to recover the investment.
Review and Extra Resources
Review Sheet Lesson 7 – Home Heating Basics
- Residential Heat Loss
- Home heating is the single highest energy expense for a household.
- Mechanisms of heat loss. You should be able to identify the mechanisms given some examples.
- Conduction
- Convection
- Radiation
- Heating Degree Days. Definition and Calculation of HDD
- Seasonal heating degree day. Calculation of Seasonal HDDs
- Heat loss
- Hourly heating loss
- From temperature difference
- Annual or Seasonal heating loss
- From HDD
- Hourly heating loss
- Insulation and Home heating fuels
- R-Value
- Types of Insulation
- Composite R-value calculation (Make sure if the component R-value is given for the whole thickness or per inch.)
- Calculation of wall heat loss
- Fuel Choices for home heating
- Heating value of fuels
- Heating Efficiency
- AFUE (Annual Fuel Utilization Efficiency)
- Energy Cost
- Annual heating
- Payback Period
- Make sure you use the correct units for each quantity used in the formula.
Test Yourself!
The questions below are your chance to test and practice your understanding of the content covered in this lesson. In other words, you should be able to answer the following questions if you know the material that was just covered! If you have problems with any of the items, feel free to post your question on the unit message board so your classmates, and/or your instructor, can help you out!
- Compare and contrast the three conventional heating methods (forced air duct, Hydronic floor, and baseboard heating systems).
- Describe any five methods (total) to reduce home heating/cooling costs, and explain how each step reduces the energy consumption.
- Explain the operation principle of a ground source heat pump. Explain the difference between an open-loop and a closed-loop GHP.
- What is the difference between active and passive heating systems?
- With a neat sketch, describe how an active solar heating system works.
- Describe any three passive heating methods.
- Explain how a geothermal heat pump works and why it is so efficient.
- Explain clearly how an air-to-air heat pump works. List the main components used in the heat pump.
Extra Resources
For more information on topics discussed in Lesson 7, see these selected references:
- ACEEE Heating [9]
- Office of Energy Efficiency and Renewable Energy [10]
- Elements of an energy efficient house [11], Factsheet,DOE/GO-102-1070 PS-207 July 2000, pp 1-8.
- Insulation, Fact sheet [12], US Department of Energy DOE/CE-0180, 2008.
- Fiber Glass Loose Fill Insulation [13]
- Q&A About Home Insulation [14]
- EERE on insulation [15]
Lesson 7 Deliverables
Deliverable 1
You must complete a short quiz that covers the reading material in lesson 7. The Lesson 7 Quiz, can be found in the Lesson 7: Home Heating Basics module in Canvas. Please refer to the Calendar in Canvas for specific timeframes and due dates.