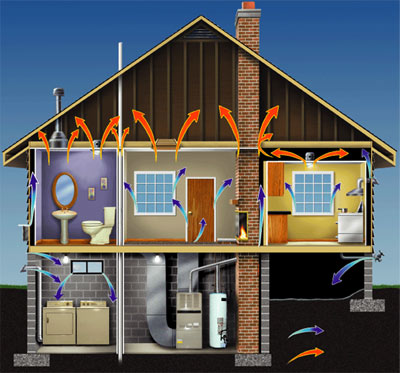
Lesson 7a: Residential Heat Loss
Houses are heated to keep the temperature inside at about 65°F when the outside temperature is lower. A house requires heat continuously because of the heat loss. Heat can escape from a house through various places; some are well known and some are not noticeable. Heat can escape from the roof, walls, doors, windows, basement walls, chimney, vents, and even the floor.
The more heat the house leaks, the more the furnace has to put out to make up for the loss. For the furnace to generate more heat to compensate the heat loss, more fuel needs to be put into the furnace, hence higher fuel or heating costs.
As you will recall from Lesson 3, not all energy conversion devices are efficient. Thus, it is important to note that furnaces are not 100 percent efficient. When a furnace’s efficiency is lower, the fuel consumption for the same amount of heat output will be even higher.
Where Does Heat Loss Occur?
Participate in the following activity to find out where the most heat loss occurs.
- Drag and drop the percentages onto the appropriate area of the home indicating where heat loss occurs.
Where Does Heat Loss Occur?
Below are the most common places for heat loss in a typical home.
- Heat loss through ceilings.
- Heat loss through windows.
- Heat loss through doors.
- Heat loss through frame walls.
- Heat loss through cracks in walls, windows, and doors.
- Heat loss through basement walls.
- Heat loss through basement floor.
Question: Which one has the most heat loss compared to the others?
Answer: # 5 Heat loss through cracks in walls, windows, and doors
Actual percentages of heat loss for each:
- Heat loss through ceilings = 5%
- Heat loss through windows = 16%
- Heat loss through doors = 3%
- Heat loss through frame walls = 17%
- Heat loss through cracks in walls, windows, and doors = 38%
- Heat loss through basement walls = 20%
- Heat loss through basement floor = 1%
Mechanisms of Heat Loss or Transfer
Heat escapes (or transfers) from inside to outside (high temperature to low temperature) by three mechanisms (either individually or in combination) from a home:
- Conduction
- Convection
- Radiation
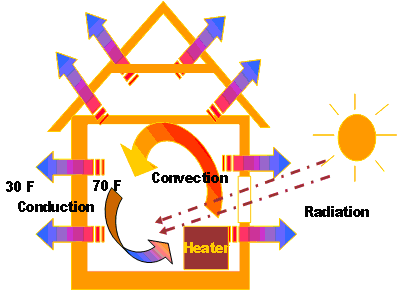
Click here to open a text description of the examples of heat transfer by conduction, convection, and radiation
- Conduction: heat moving through walls of a home from high temperature inside to low temperature outside.
- Convection: heat circulating within the rooms of a house.
- Radiation: Heat from the sun entering a home.
Conduction
Conduction is a process by which heat is transferred from the hot area of a solid object to the cool area of a solid object by the collisions of particles.
In other words, in solids the atoms or molecules do not have the freedom to move, as liquids or gases do, so the energy is stored in the vibration of atoms. An atom or molecule with more energy transfers energy to an adjacent atom or molecule by physical contact or collision.
In the image below, heat (energy) is conducted from the end of the rod in the candle flame further down to the cooler end of the rod as the vibrations of one molecule are passed to the next; however, there is no movement of energetic atoms or molecules.
Click the play button to start the animation.
Click here to open a text description of the Conduction Candle animation
Example of Conduction
A hand holds a metal rod above a lit candle. The molecules quickly heat up at the point where the flame touches the rod. The heat then spreads across the entire metal rod, and the heat is then able to be felt by the hand.
With regard to residential heating, the heat is transferred by conduction through solids like walls, floors, and the roof.
Click the play button to start the animation.
Click here to open a text description of Conduction in Regard to Residential Heating example
Example of Conduction in Regard to Residential Heating
Picture the cross-section of a wall in a house. Inside the house it is 65°F and outside it is 30°F. Two arrows point from inside the house to the outside to show how heat is transferred from the inside of the house to the outside through the wall via conduction.
Convection
Convection is a process by which heat is transferred from one part of a fluid (liquid or gas) to another by the bulk movement of the fluid itself. Hot regions of a fluid or gas are less dense than cooler regions, so they tend to rise. As the warmer fluids rise, they are replaced by cooler fluid or gases from above.
In the example below, heat (energy) coming from candle flame rises and is replaced by the cool air surrounding it.
Click the play button to start the animation.
Click here to open a text description of the Convection Candle animation
Example of Convection
A hand is held above a lit candle. As the candle heats the air, the heat rises to the hand. Eventually, it gets too hot, and the hand pulls away from the candle.
In residential heating, convection is the mechanism by which heat is lost by warm air leaking to the outside when the doors are opened, or cold air leaking into the house through the cracks or openings in walls, windows, or doors. When cold air comes in contact with the heater in a room, it absorbs the heat and rises. Cold air, being heavy, sinks to the floor and gets heated, and thus slowly heats the whole room air.
Instructions: Press the play button below and observe what happens to the cold air (blue arrows) as it enters the house and encounters the warm air (red arrows) coming from the heating vent:
Click here to open a text description of the Convection in a Room animation
Example of Convection in Regard to Residential Heating
Picture a room with an open door letting in cool air on the left and a radiator creating heat on the right. As the radiator heats the air around it, the air rises and is replaced by cool air. Once the warm air hits the ceiling, it travels left towards the open door, cooling as it moves. The cool air from the open door travels to the right across the floor towards the radiator to be heated. The overall effect is a circular convection current of air within the room.
Radiation
Radiation is the transfer of heat through electromagnetic waves through space. Unlike convection or conduction, where energy from gases, liquids, and solids is transferred by the molecules with or without their physical movement, radiation does not need any medium (molecules or atoms). Energy can be transferred by radiation even in a vacuum.
In the image below, sunlight travels to the earth through space, where there are no gases, solids, or liquids.
Click the play button to start the animation.
Click here to open a text description of the Radiation Example animation
Example of Radiation
Picture the Sun and the Earth, with arrows traveling from the Sun to the Earth through space. The arrows represent the energy that travels to the Earth via radiation, which does not require any medium (atoms or molecules) to do so.
Test Yourself
First, identify the type of home heat loss pictured in images A-J as either: conduction, convection or radiation. Then click and drag each image down to the correct category at the bottom of the screen.
Click here to open a text description of the Test Yourself activity
Test Yourself: Types of Heat Loss
Identify the type of heat loss (conduction, convection, or radiation) for each of the following examples:
- Heat escaping through the roof of a house
- A hot stove burner
- Boiling water
- A torch halogen lamp producing light and heat
- A door hanging wide open, letting in cold air
- A fire creating heat
- Heat escaping through a wall
- A mirror reflecting sunlight
- Heat escaping through a window
- Heat escaping through a chimney
Answers:
A. Conduction
B. Radiation
C. Convection
D. Radiation
E. Convection
F. Radiation
G. Conduction
H. Radiation
I. Conduction
J. Radiation
Reducing Energy Consumption
There are two ways in which we can reduce energy consumption.
- The most cost-effective way is to improve the home’s “envelope”—the walls, windows, doors, roof, and floors that enclose the home—by improving the insulation (conduction losses) and sealing the air leaks with caulking (convection losses).
- The second way to reduce the energy consumption is by improving the efficiency of the furnace that provides the heat.
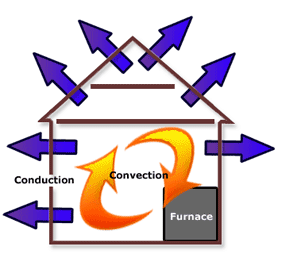
Click here to open a text description of the Conduction and Convection diagram
Line drawing of a house with arrows pointing out from the walls and roof showing conduction & arrows flowing in a circular motion inside the house showing convection.
Conduction Heat Loss
Main Factors of Heat Loss
What does a house's heat loss depend on? Complete the activity below to find out the three main factors leading to heat loss.
Main Factors of Heat Loss
What are the three main factors a house's heat loss depends on?
Example 1:
House A sits next to house B. Though both houses have the same basic design, house B is significantly larger than house A.
- Which house loses more heat?
- House A
- House B
- Why do you think this house loses more heat?
- More people in it
- More appliances and lights are used
- Larger size/more area
Example 2:
House A and house B are the exact same size and design. House A sits on the beach in a warm, tropical area, while house B sits by a ski resort in the mountains up north, surrounded by snow.
- Which house loses more heat?
- House A
- House B
- Why do you think this house loses more heat?
- People skiing need more heat to keep warm
- Snow on the roof is good insulation
- Outside temperature
Example 3:
House A and house B are the same size and sit next to each other. The design for both houses is the same, except house A has a thick layer of pink insulation installed. The R-value of house B is .63 and the R-value of house A is unknown.
- Which house loses more heat?
- House A
- House B
- Why do you think this house loses more heat?
- Less insulation
- It's only one color
- It's thicker
Answers:
Example 1:
- B: House B
- C: Larger size/more area
Example 2:
- B: House B
- C: Outside temperature
Example 3:
- B: House B
- A: Less insulation
Most heat is lost through a house's walls through conduction. As you learned from the activity on the previous screen, the amount of heat loss depends on three factors:
- Size of the house (area through which the heat can escape)
- Local weather or climatic conditions:
- The inside temperature is often constant at a comfortable temperature of 65°F.
- As the outside temperature falls lower than 65°F, the heat is lost to the outside.
- The higher the temperature difference, the higher the heat loss to outside.
- By calculating the Heating Degree Days (HDD), we can determine how many degrees the mean temperature fell below 65ºF for the day.
- Wall's capacity to resist heat loss.
- Insulation is rated in terms of thermal resistance, called R-value, which indicates the resistance to heat flow.
- The higher the R-value, the greater is the insulating effectiveness.
Heating Degree Days
Local weather or climatic conditions are one of three factors that affects the amount of heat loss through conduction. When examining weather conditions, we look at both the inside and outside temperature of a home.
The inside temperature is usually taken as a standard comfort temperature of 65ºF. The outside temperature varies by the hour. Knowing this information can help us to understand two concepts:
- Average outside temperature = Average of the maximum and minimum temperature during the day
- Heating Degree Day (HDD) = The temperature difference through which air has to be treated, or how many degrees the mean temperature fell below 65ºF for the day. It is also an index of fuel consumption.
Determining Heating Degree Day (HDD)
The formula for determining the Heating Degree Day (HHD) is:
To calculate HDD:
- Determine the base temperature or inside temperature:
- Find the day's average outside temperature using this formula:
- Use the HDD formula to solve:
Try This!
Click the play button below, and observe the temperature changes. Then calculate the average temperature and the Heating Degree Day.
Click here to open a text description of the Heating Degree Days activity.
Try This: Determining Heating Degree Day (HDD)
Picture a house with a thermometer on the porch. The current outside temperature is 60 degrees. As thick clouds start to move in, the temperature begins to drop in 5 degree increments, first to 55 degrees, then 50 degrees, etc. When the clouds have completely blocked the Sun, the thermometer reads 40 degrees.
Questions:
- What is the average temperature?
Hint: Ta = (max temperature + minimum temperature) divided by 2. - What is the heating degree days?
Hint: HDD = Tbase - Ta
Answers:
- 50 degrees
- 15 degrees
Heating Degree Days Examples
Example 1
Calculate the HDD for one day when the average outside temperature is 13º F.
Calculate the HDD for one day when the average outside temperature is 2º C.
Example 2
Given the following data, calculate the HDD for the week:
| Day | Average Temperature |
|---|---|
| Sunday | 49° F |
| Monday | 47° F |
| Tuesday | 51° F |
| Wednesday | 60° F |
| Thursday | 65° F |
| Friday | 67° F |
| Saturday | 58° F |
Heating Degree Day
For this problem, we need to calculate HDD for one full week. The data that is given is each day, what is the outside temperature -- average outside temperature. For example, Sunday, the average outside temperature is 49 degrees F. Monday 47 degrees Fahrenheit, Tuesday it’s 51 and Wednesday it is 60 degrees F and on Thursday it is 65, Friday, 67 and on Saturday it is 58.
| Day | Temperature (°F) |
|---|---|
| Sunday | 49 |
| Monday | 47 |
| Tuesday | 51 |
| Wednesday | 60 |
| Thursday | 65 |
| Friday | 67 |
| Saturday | 58 |
So we need to calculate heating degree days (HDD) for each day. One day, that is Sunday, the outside temperature is 65 minus 49 the outside temperature will give you the degree days. Similarly, 65 minus 47° Fahrenheit, one day times 65 minus 51 in this case. One day times 65 minus 60 and one day 65 minus 65. This would be zero. One day 65 minus 67. Remember when it exceeds 65, the heating degree days would be zero. In this case, also it is zero. One day on Saturday it is 65 minus 58.
| Day | Temperature (°F) | Calculate HDD |
|---|---|---|
| Sunday | 49 | 1 day (65-49) |
| Monday | 47 | 1 day (65-47) |
| Tuesday | 51 | 1 day (65-51) |
| Wednesday | 60 | 1 day (65-60) |
| Thursday | 65 | 1 day (65-65)=0 |
| Friday | 67 | 1 day (65-67)=0 |
| Saturday | 58 | 1 day (65-58) |
This case it is 7.
| Day | Temperature (°F) | Calculate HDD |
|---|---|---|
| Sunday | 49 | 1 day (65-49)=16 |
| Monday | 47 | 1 day (65-47)=18 |
| Tuesday | 51 | 1 day (65-51)=14 |
| Wednesday | 60 | 1 day (65-60)=5 |
| Thursday | 65 | 1 day (65-65)=0 |
| Friday | 67 | 1 day (65-67)=0 |
| Saturday | 58 | 1 day (65-58)=7 |
These two are zeros, this is 5 and this is 14 and this happens to be 18 and here it is 16. So the total sum is for one full week is 60 degree days.
| Day | Temperature (°F) | Calculate HDD |
|---|---|---|
| Sunday | 49 | 1 day (65-49)=16 |
| Monday | 47 | 1 day (65-47)=18 |
| Tuesday | 51 | 1 day (65-51)=14 |
| Wednesday | 60 | 1 day (65-60)=5 |
| Thursday | 65 | 1 day (65-65)=0 |
| Friday | 67 | 1 day (65-67)=0 |
| Saturday | 58 | 1 day (65-58)=7 |
| Total | 60 Degrees |
This is equal to 60 degree days.
Seasonal Heating Degree Days
In previous examples, we are assuming that the outside temperature remains the same for all 150 heating days in a season. This is not realistic, but it explains the method to calculate the HDD. In a more realistic example, we need to find the temperature difference for each day and add all the temperature differences.
We will now look at Seasonal Heating Degree Days (HDD), which is the sum of temperature differences of ALL days - rather than just 1 day or 1 week - during which heating is required.
The table below provides Seasonal HDDs for selected places in the United States. The higher HDD indicates a higher heat loss and therefore, higher fuel requirements.
HDD is used to estimate the amount of energy required for residential space heating during a cool season, and the data are published in local newspapers or on the National Weather Service website.
| Place | Degree Days |
|---|---|
| Birmingham, AL | 2,823 |
| Anchorage, AK | 10,470 |
| Barrow, AK | 19,893 |
| Tucson, AZ | 1,578 |
| Miami, FL | 155 |
| Pittsburgh, PA | 5,829 |
| State College, PA | 6,345 |
Source: NOAA [2]
Calculating Seasonal Heating Degree Days
To calculate Seasonal Heating Degree Days, use this formula:
Remember, in months where the average temperature is equal to or greater than 65, there will be no heating degree days, so the value for the month will be 0.
Seasonal Heating Degree Days Examples
Example 1
Given the following set of average temperatures, by month, for State College, PA, calculate the HDD for the heating season:
| Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 25°F | 28°F | 37°F | 48°F | 59°F | 67°F | 71°F | 70°F | 62°F | 51°F | 41°F | 31°F |
Please watch the following (2:32) presentation about problem #1:
Lesson 7a, Screen 23: Seasonal Heating Degree Days
Example 3
Given the following set of average temperatures, by month, for State College, PA, calculate the HDD for the heating season:
| Jan | Feb | Mar | Apr | May | Jun | July | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 °F | 28 °F | 37 °F | 48 °F | 59 °F | 67 °F | 71 °F | 70 °F | 62 °F | 51 °F | 41 °F | 31 °F |
Alright, this is an interesting problem. Given the following temperatures by month for State College, we need to calculate the heating degree days for the entire season. For January, the outside temperature is 25° F. This is average temperature for 31 days in January. And February, the outside temperature is 28° F, March, 37° F and April it is 48° F and May, the temperature outside is 59° F. June, the outside temperature is 67° F, July, the outside temperature is 71° F and August it is 70° F. September, it goes on like that. September it is 62° F, and October it is 51° F, November, 41° F and December goes as 31° F.
What we need to do is basically subtract this number (25° F) from 65 so the difference is, 65 minus 25, so this is 40° F for the month of January.
The same case here (February). 65 minus 28 which happens to be 37° F.
And if we do the same for all these months, from March through December, and then we have to multiply each month temperature difference by the number of days in the month.
So, for example, in the case of January, there are 31 days. So when you multiply 40◦ by 31 days you get 1240 degree days.
Similarly, we can do for all these months and add up and it turns out that for the entire year, it is 6138 degree days is for State College.
Example 2
If Ms. S. Belle moves from Birmingham, AL (HDD=2,800) to State College, PA (HDD=6,000) how much can she expect her heating bill to increase?
Please watch the following 1:34 presentation about problem #2:
Lesson 7a, Screen 24: Seasonal Heating Degree Days
Example 4
If Ms. S. Belle moves from Birmingham, AL (HDD = 2,800) to State College, PA (HDD=6,000) how much can she expect her heating bill to increase?
Alright, this is problem 1.6, if Ms. S. Belle moves from Birmingham, AL to State College, how much can she expect her heating bill to increase?
Birmingham, AL has heating degree days of 2800 and State College, PA has 6000. We need to remember this 6000 degree days. Basically what’s happening here is she is going to be heating more her home and it is increasing from 2800 to 6000. So, her increase is 6000 minus 2800 will be 3200 degree days.
And this increase (3200) is how much compared to 2800 what she has been paying for. So the increase is 3200 compared to the baseline of 2800. We need to multiply this by 100 to get the percentage. It would be an increase of 114 %.
She would be spending about 114% more for her heating in State College, PA.
Calculating Hourly Heat Loss
As we have learned, most heat is lost through a house's walls through conduction. One of the three factors that affect heat loss is a wall's capacity to resist heat loss.
We will now look at how to calculate the rate of heat loss of the walls of a house, using the following formula:
From the above equation, it can be seen that once the house is built, these two variables will NOT change:
- The area of the walls
- The R-value of the walls
The only variable that will change is the temperature difference between inside and outside.
Example
Calculate the heat loss for a 10 ft by 8 ft wall, insulated to R-value 22. The inside temperature is maintained at 70° F. The temperature outside is 43° F.
Please watch the following 2:25 presentation about Hourly Heat Loss:
Lesson 7a, Screen 26: Calculating Hourly Heat Loss
Example 5
Calculate the heat loss for a 10 ft by 8 ft wall, insulated to R-value 22. The inside temperature is maintained at 70°F. The temperature outside is 43°F.
For this problem, we are trying to calculate the heat loss. We are given the dimensions; we are given the R-value and the temperature difference. Those are the quantities that we need to calculate the heat loss, basically.
The dimensions are, the wall dimensions are 8ft and this side is 10 ft.
So the area is 8 times 10 will be 80 foot square or 80 square feet. And we are also given the inside temperature is 70°F and outside temperature, average outside temperature, is 43°F. Therefore, the difference or delta T (ΔT) is equal to 27°F.
Now area is given, A is, we already calculated 80ft2 and R-value is also given as 22 which is 22 ft2 °F hour over BTU.
Now, heat loss, BTUs per hour, is equal to area times ΔT divided by R-value.
Now in this case, it is:
So this will be equal to, here you can cancel ft2 and this ft2 and this °F and this °F, and we are left with BTUs per hour. And the heat loss comes out to be 98.2 BTU/h.
Calculating Daily Heat Loss
Now that you know how to calculate hourly heat loss, how would you calculate daily heat loss?
Since there are 24 hours in a day, you would simply multiply the hourly heat loss by 24.
Example
What is the hourly and daily heat loss of a 15-ft by 15-ft room with an 8-ft ceiling, with all surfaces insulated to R13, with inside temperature 65°F and outside temperature 25°F?
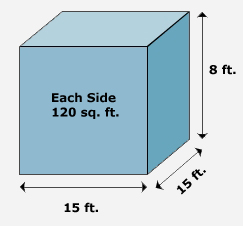
Once we know the heat loss rate per hour, we can determine the heat loss per day by multiplying by 24 (hours in a day).
In a 24-hour period or one day, the heat loss would be:

Area (ft2) is the sum of the area of all four walls. Each wall is 8' x 15', or 120 sq. feet, so take 4 x 120 sq ft to get 480 ft2 in the equation.
Calculating Annual Heat Loss
In the previous calculations, we determined hourly and daily heat loss. How do we calculate annual or seasonal heat loss?
Since the temperature outside the house may not remain the same day after day, the heat loss will vary by the day. Thus, to obtain the heat loss for a whole year, we do the following:
- Calculate heat loss for each day.
- Add the heat loss for all days in a year that needed heating.
- Leave the R-value of the wall and the area of the wall the same – they will not change.
- Determine the difference between inside and outside temperature, since it will change for each day.
Recall that the formula for daily heat loss is:
Thus, theoretically, we would need to perform this calculation for every day of the 365-day calendar year.
For example, if the average outside temperature were to be 35°F, 32°F, 28°F, and so on for each day, the heat loss for the whole year or the season can be calculated as follows:
Since the area (480 ft2), R-value ,and 24 h in a day are common for ALL heating days, we can bring those out and rewrite the equation as:
This equation can be even further simplified. The formula for Annual or Seasonal heat loss can be written in general terms as:
Calculating Annual Heat Loss Examples
Example 1
Please watch the following 3:29 presentation on Example Problem #1. For the 150-day heating season in Roanoke, VA, the average temperature was 47° F. How much heat is lost through a 176 ft2 wall (R=16) during the entire season?
Lesson 7a, Screen 32: Calculating Annual or Seasonal Heat Loss
Example 7 (formerly Example 3-11)
For the 150-day heating season in Roanoke, VA, the average temperature was 47°F.
How much heat is lost through a 176 ft2 wall (R=16) during the entire season?
Ok. In this problem, 3-11, we are trying to calculate the heat loss for a 150-day season in Roanoke, VA. It is a 150-day heating season. The outside temperature is given as 47°F. Inside, is obviously 65°F. Ok?
Outside: 47°F
Inside: 65°F
Degree Days can be calculated like this. Heating Degree Days are equal to the number of days, which is 150 in a season here, times the temperature difference. 65 minus 47°F.
Now we can calculate that. That is equal to 150 days times 18. So that turns out to be 2700 °F days.
Now, what else do we need? We need the area. Area is given. Area is equal to 176 ft2, and we are also given the R-value. R-value is 16.
Therefore, we can calculate the heat loss, heat loss through a season. Heat loss through the season is equal to Area times HDD times 24 over R.
Now, what can we cancel? ft2/ ft2, °F/°F, hour/hour and days/days are canceled. So when we do this calculation here, we get the answer of 712,800 Btus in this 150 day heating season.
Example 2
Please watch the following 3:42 presentation on Example Problem #2. In Fargo, ND, the heating season lasts about 220 days and the average outside temperature is around 27° F. How much heat is lost through an 8 ft by 6 ft window (R=1) during the heating season?
Lesson 7a, Screen 33: Calculating annual or Seasonal Heat Loss
Example 8 (formerly example 3-12)
In Fargo, ND, the heating season lasts about 220 days and the average outside temperature is around 27°F. How much heat is lost through an 8 ft by 6 ft window (R=1) during the heating season?
This problem is very similar to the last one, 3-11. Now this 3-12 involves again heat loss through a season. We need to calculate the HDD’s. The heating days are 220 days. Now the temperature difference is, inside, 65°F as usual and outside, the temperature, the average temperature happens to be 27°F for all 220 days. Therefore, Heating Degree Days (HDD) can be calculated like this: 220 days times (65°F minus 27°F). And this is equal to 220 days times 38°F which is equal to 8,360°F days.
Now, do we know the area? Area is given, actually. The dimensions of the window are 8ft by 6ft. Therefore the area is 8ft times 6ft, which is 48ft2
We know the temperature difference, we know the HDD, and we can calculate the heat loss provided we have the R value. R-value is also given. 1 ft2 °F h over BTU.
Now it is easy to calculate heat loss. Heat loss for the season is equal to area (and I am trying to repeat this), area times HDD times 24 over R. So in this case it is, area is 48 ft2 and we have 8360 degree days times 24 hours divided by a day over R value of 1 ft2 °F h/BTU.
So ft2/ft2, °F/°F will be canceled, hours and hours are canceled, days and days are canceled here.
So, when you do this math, it comes out to be 9,630,720 BTUs. This is in one full season.