Lesson 7b: Insulation and Home Heating Fuels

The following section of Lesson 7 wil discuss insulation and home heating fuels.

R-Value

As you may recall from the first part of this lesson, R-value is a wall's capacity to resist heat loss or its thermal resistance. Insulation materials are rated in terms of their R-value, with a higher R-value indicating better insulating effectiveness.

The R-value of thermal insulation depends on the type of material, its thickness, and its density. Generally, walls are not made up of just one material or one layer.

R-values for most commonly used building materials are given in the table below. From looking at the table below, we can see that natural materials like stone and bricks are not good insulation materials, but most of the synthetic insulation products such as polystyrene or polyurethane are very effective insulation materials.

Building Materials and their R-Values
Material	R-Value (ft^{2 o} F h / BTU)
Plain glass, 1/8 inch	0.03
Stone per inch	0.08
Common Brick per inch	0.20
Asphalt Roof Shingles	0.44
1/2 inch Gypsum Board (Drywall or plasterboard)	0.45
Wood Siding, 1/2 inch	0.81
Plywood, 3/4 inch	0.94
Insulating sheathing, 3/4 inch	2.06
Fiberglass, per inch (battens)	3.50
Polystyrene per inch	5.00
Polyurethane Board	6.25

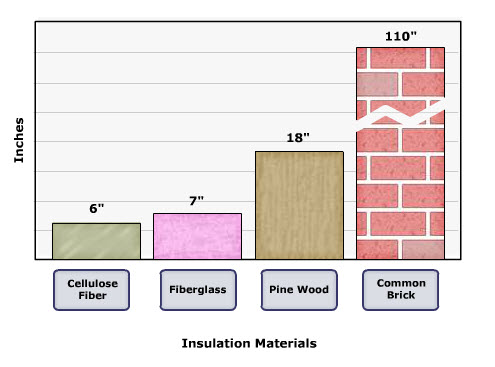
If insulation materials have a low R-value per inch, then they will need to be thicker than those materials with a higher R-value per inch to achieve the same degree of effectiveness in resisting heat loss.

Look at the chart below to compare the thickness required of various insulation materials to achieve the same R-Value of 22 and then answer the questions below.

Thickness required of various insulation materials to achieve an R-Value of 22.

Credit: "Insulation Value Of CMAA Australia [1]." LAT Works Construction.

Types of Insulation

Look at the table below to learn about six types of insulation.

Types of Insulation
Insulation	What is it made of?	What does it look like?	Additional Information
Fiberglass	Molten glass spun into microfibers	Pink or yellow in the form of batts or rolled blankets.
Rock Wool	Rock	Gray or brown fibers in batts or blankets or as shredded loose-fill.	Manufactured in a similar way as fiberglass, but with molten rock instead of glass.
Cellulose	Recycled paper – newsprint or cardboard shredded into small bits of fiber.	Blown in as loose fill.	It is treated with fire- and insect-resistant chemicals.
Rigid Foam	Different types, but some made from post-consumer recycled content from fast food containers and cups.	Rigid sheets that are applied directly to framing.	Best where space is limited, but a high R-value is needed. Can be installed on the interior of a wall, but if installed inside, must be covered by a fire resistant material like wallboard. One drawback to foam is it deteriorates unless it is protected from prolonged exposure to sunlight and water. It is also more expensive than other insulation.
Synthetic Insulation	Usually polystyrene or polyurethane foam.	Polystyrene comes as rigid boards, and Polyurethane comes as rigid boards or sprayed in place systems.	Polystyrene is used for insulating basements, cathedral ceilings, or sidewalls. Polyurethane foams are high performance insulating materials.

Composite Wall R-Values

Generally, walls are made up of several layers of different materials. The R-value of a composite wall is calculated by adding the effective R-values of each of the layers of the wall.

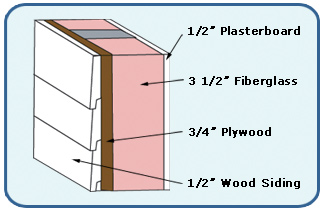
For example, the image below shows a wall made up of four layers—½ inch drywall inside for aesthetic purposes, real insulation in between the studs, ¾ inch plywood sheathing outside, and wood siding as the final exterior finish. Together, the layers of the wall are preventing heat loss.

Wall made up of four layers. The four layers are described in the paragraph above.

Diagram of a wall

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [2]

We can calculate this wall’s composite R-value by adding the R-values of each layer.

Plasterboard (1/2 inch)
+ Fiberglass (3.5 inches @ 3.70 per inch)
+ Plywood (3/4 inches)
+ Wood Siding (1/2 inch)
-----------------------------------------
Total R-Value of Composite Wall

We can find the R-values for the walls by using the table from the page about R-Values [3] (the table is repeated below):

Building Materials and their R-Values
Material	R-Value (ft^{2 o} Fh / BTU)
Plain glass, 1/8 inch	0.03
Stone per inch	0.08
Common Brick per inch	0.20
Asphalt Roof Shingles	0.44
1/2 inch Gypsum Board (Drywall or plasterboard)	0.45
Wood Siding, 1/2 inch	0.81
Plywood, 3/4 inch	0.94
Insulating sheathing, 3/4 inch	2.06
Fiberglass, per inch (battens)	3.50
Polystyrene per inch	5.00
Polyurethane Board per inch	6.25
Cinder Block (12 inches)	1.89

Plasterboard (1/2 inch) = 0.4524
+ Fiberglass (3.5 inches @ 3.70 per inch) = 12.95
+ Plywood (3/4 inches) = 0.94
+ Wood Siding (1/2 inch) = 0.81
-----------------------------------------
Total R-Value of Composite Wall = 15.15 $\frac{{ft}^{2} ° Fh}{Btu}$

Examples

Example 1

A ceiling is insulated with 0.75" plywood, 2" of polystyrene board, and a 3" layer of fiberglass. What is the R-Value for the ceiling?

Solution:

The ceiling consists of three layers, and all three layers together prevent the heat loss. So, we need to add the R-values of all three layers

$\frac{3/}{4}$ " of plywood has an R-value of 0.94
2" of polystyrene at 5.0 per inch will have an R-value of 10.00
3" of fiberglass at 3.7 per inch will have an R-value of 11.10

So the R-value of the ceiling is 22.04 ft^{2 o}Fh / BTU.

Pink insulation in the ceiling

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [2]

Example 2

Please watch the following 1:31 video presentation about Example #2. A wall consists of 0.5” wood siding (R = 0.81), 0.75” plywood (R = 0.94), 3.5” of fiberglass (R = 13.0), and 0.5” plasterboard (R = 0.45). What is the composite R-value of the wall?

Click here for a transcript of Composite Wall R-Values Problem # 1 video.

Lesson 7b, Screen 7: Composite Wall R-Values

Example 10

This problem, we need to calculate composite R-value.

The wall consists of four layers. One half inch wood siding, and its R-value is given straight away for half inch as .81. And we have three-quarter inch plywood and this plywood’s R-value is also given as .94, this is for 3/4". Whereas the fiberglass, each inch has an R-value of 3.7. We are using 3 and a half inches. So, 3.5 times 3.7 would give us about 13.00 R-value. And the last layer would be one half inch plaster board which is also drywall and its R-value is given as .45.

1/2" wood siding: 0.81
3/4" plywood: 0.94
3 1/2 Fiberglass (3.7/inch): 13.00
1/2" plaster board: 0.45
Total: 15.2

So when you add these up you get 15.2 which means the composite R-value of this wall is 15.2 degrees F, foot squared, hour over BTUs.

= 15.2 \frac{° F f t^{2} h}{B T U}

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [2]

Example 3

Please watch the following 1:18 video presentation about Example #3. What is the R-value of a wall that is made up of wood siding (R = 0.81), 5” of fiberglass (R = 3.70 per inch), and a layer of 0.5” drywall (R = 0.45)?

Click here for a transcript of Composite Wall R-Values Problem #2 video.

Lesson 7b, Screen 8: Composite Wall R-Values

Example 11

What is the R-value of a wall that is made up of wood siding (R= 0.81), 5” of fiberglass (R=3.70 per inch), and a layer of .5” drywall (R=0.45)?

Here we have, again a wall made up of three different layers. The first layer is wood siding which is outside, obviously, and its R-value is given as 0.81, whatever the thickness might be of that wood siding. And we have a second layer of fiberglass. And this fiberglass thickness is given as 5” and its R-value is given as 3.7 per inch. So we are using 5 inches so 5 times 3.7 would be 18.50. And we have a third layer of a drywall and this drywall has an R-value of 0.45, half inch drywall.

Wood siding: 0.81
5" fiberglass 3.7/inch: 18.50 (5x3.7)
Drywall: 0.45
Total R-value: 19.76

When you add all these three layers up, you get a total R-value of 19.76.

So the answer is 19.76 degrees F, foot squared, hour over BTUs. This is the composite R-value.

C o m p o s i t e R - v a l u e = 19.76 \frac{° F f t^{2} h}{B T U}

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [2]

Example 4

Please watch the following 1:44 video presentation about Example #4. A wall is made up of 8” of stone, 3” of polyurethane board, and 0.75” of plywood. Calculate the composite R-value for the wall.

Click here for a transcript of Composite Wall R-Values Problem #3 video.

Lesson 7b, Screen 9: Composite Wall R-Values

Example 12

A wall is made up of 8” of stone, 3” of polyurethane board, and 0.75” of plywood. Calculate the composite R-value for the wall.

This is a problem where we have three layers for a wall and those three layers are made up of stone, polyurethane board and plywood. The first one is stone and its thickness is 8” and each inch of stone wall will provide an R-value of 0.08. Therefore, all these 8” together would provide 0.64. And the second layer is made up of 3” of polyurethane and each inch provides an R-value of 6.25, therefore, together, all 3” would provide an R-value of 18.75. The third layer is again three quarters inch plywood, and it provides an R-value of 0.94. So all these three together would have an R-value of 20.33 or the composite R-value is 20.33 degree F, foot squared, hour over BTUs.

8" stone (0.08/inch): 0.64
3" polyurethane (6.25/inch): 18.75
0.75" plywood: 0.94
Total: 20.33

C o m p o s i t e R - v a l u e = 20.33 \frac{° F f t^{2} h}{B T U}

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [2]

Insulation Needs By Region

The United States map below shows insulation needs by region, as indicated by color and numbers.

Instructions: Click on the “zone” buttons below the map to see the U.S. Department of Energy’s Recommended Total R-Values for new construction of houses. Note that insulation R-values are different for the ceilings, walls, floor, etc.

U.S. Department of Energy recommended total R-Values for new construction houses, by regions and by various parts of the house.

Insulation Needs activity

Click here to open a text description of the Insulation Needs activity

Insulation Needs by Region

The U.S. Department of Energy released recommended total R-values for new construction houses. The info is based on regional zone and covers various parts of the house. The states within each zone are listed below, followed by a data table containing the R-values for each part of the house. The R-values are dependent on the type of heating system being used and may vary for each. Some states may lie in multiple zones.

Zone 1

States:

Florida

Zone 1 Insulation Needs
Zone 1	Gas Heat Pump Fuel Oil	Electric Furnace
Attic	R-49	R-49
Cathedral Ceiling	R-38	R-60
Wall	R-18	R-28
Floor	R-25	R-25
Crawl Space	R-19	R-19
Slab Edge	R-8	R-8
Basement Interior	R-11	R-19
Basement Exterior	R-10	R-15

Zone 2

States:

California
Arizona
Texas
Louisiana
Mississippi
Alabama
Florida
Georgis

Zone 2 Insulation Needs
Zone 2	Gas Heat Pump Fuel Oil	Electric Furnace
Attic	R-49	R-49
Cathedral Ceiling	R-38	R-38
Wall	R-18	R-22
Floor	R-25	R-25
Crawl Space	R-19	R-19
Slab Edge	R-8	R-8
Basement Interior	R-11	R-19
Basement Exterior	R-10	R-15

Zone 3

States:

North Carolina
South Carolina
Georgia
Alabama
Mississippi
Tennessee
Louisiana
Arkansas
Oklahoma
Texas
New Mexico
Arizona
Utah
New Mexico
Nevada
California
Alaska

Zone 3 Insulation Needs
Zone 3	Gas Heat Pump Fuel Oil Electric Furnace
Attic	R-49
Cathedral Ceiling	R-38
Wall	R-18
Floor	R-25
Crawl Space	R-19
Slab Edge	R-8
Basement Interior	R-11
Basement Exterior	R-10

Zone 4

States:

New York
New Jersey
Maryland
Delaware
Virginia
Pennsylvania
West Virginia
Ohio
Indiana
Illinois
Kentucky
Tennessee
North Carolina
Georgia
Arkansas
Missouri
Kansas
Oklahoma
Colorado
Texas
New Mexico
Arizona
California
Oregon
Washington

Zone 4 Insulation Needs
Zone 4	Gas Heat Pump Fuel Oil	Electric Furnace
Attic	R-38	R-49
Cathedral Ceiling	R-38	R-38
Wall	R-13	R-18
Floor	R-13	R-25
Crawl Space	R-19	R-19
Slab Edge	R-4	R-8
Basement Interior	R-11	R-11
Basement Exterior	R-4	R-10

Zone 5

States:

Washington
Oregon
Idaho
California
Nevada
Utah
Colorado
Arizona
New Mexico
Wyoming
South Dakota
Nebraska
Kansas
Iowa
Missouri
Illinois
Michigan
Indiana
Ohio
Pennsylvania
New York
West Virginia
Maryland
New Jersey
New Hampshire
Massachusetts
Rhode Island
Connecticut

Zone 5 Insulation Needs
Zone 5	Gas	Heat Pump Fuel Oil	Electric Furnace
Attic	R-38	R-38	R-49
Cathedral Ceiling	R-30	R-38	R-38
Wall	R-13	R-13	R-18
Floor	R-11	R-13	R-25
Crawl Space	R-13	R-19	R-19
Slab Edge	R-4	R-4	R-8
Basement Interior	R-11	R-11	R-11
Basement Exterior	R-4	R-4	R-10

Zone 6

States:

California
Washington
Idaho
Wyoming
Montana
Utah
Colorado
North Dakota
South Dakota
Minnesota
Iowa
Wisconsin
Michigan
New York
Pennsylvania
Vermont
New Hampshire
Maine

Zone 6 Insulation Needs
Zone 6	Gas	Heat Pump Fuel Oil	Electric Furnace
Attic	R-22	R-38	R-49
Cathedral Ceiling	R-22	R-30	R-38
Wall	R-11	R-13	R-18
Floor	R-11	R-11	R-25
Crawl Space	R-11	R-13	R-19
Slab Edge	(c)	R-4	R-8
Basement Interior	R-11	R-11	R-11
Basement Exterior	R-4	R-4	R-10

Source: Office of Energy Efficiency & Renewable Energy [4]

Calculating Wall Heat Loss

Heat loss from the surface of a wall can be calculated by using any one of the three formulas we have covered in Part A of this Lesson.

Equations

The heat loss in an hour equation

$H e a t L o s s (\frac{B T U s}{h}) = \frac{A r e a (f t^{2}) \times T e m p . D i f f e r e n c e (^{o} F)}{R - V a l u e \frac{f t^{2}^{o} F h}{B T U}}$

The heat loss in a day equation

$H e a t L o s s (\frac{B T U s}{h}) = \frac{A r e a (f t^{2}) \times T e m p . D i f f e r e n c e (^{o} F)}{R - V a l u e \frac{f t^{2}^{o} F h}{B T U}} \times 24$

The heat loss in full heating season

$S e a s o n a l H e a t L o s s = \frac{A r e a}{R - V a l u e} \times 24 \times H D D$

The heat loss from walls, windows, roof, and flooring should be calculated separately, because of different R-Values for each of these surfaces. If the R-value of walls and the roof is the same, the sum of the areas of the walls and the roof can be used with a single R-value.

Example

A house in Denver, CO has 580 ft² of windows (R = 1), 1920 ft² of walls and 2750 ft² of roof (R = 22). The walls are made up of wood siding (R = 0.81), 0.75” plywood, 3.5” of fiberglass insulation, 1.0” of polyurethane board, and 0.5” gypsum board. Calculate the heating requirement for the house for the heating season, given that the HDD for Denver is 6,100.

Solution:

Heating requirement of the house = Heat loss from the house in the whole year. To calculate the heat loss from the whole house, we need to calculate the heat loss from the walls, windows, and roof separately, and add all the heat losses.

Heat loss from the walls:

Area of the walls = 1,920 ft², HDD = 6,100, and the composite R- value of the wall needs to be calculated.

Materials and their R-Value
Material	R-Value
Wood Siding	0.81
3/4 inch plywood	0.94
3.5 inches of fiberglass 3.5 in x 3.7 / in	12.95
1.0 inch of polyurethane board = 1.0 in x 5.25 / in	5.25
1/2 inch Gypsum board	0.45
Total R-Value of the walls	20.40

Heat Loss from Walls = \frac{1,920 {ft}^{2} \times 6,100 ° F - days \times \frac{24 h}{day}}{20 .4 \frac{{ft}^{2} ° F h}{Btu}} = 13 .78 MMBtu

Heat Loss from Windows = \frac{580 {ft}^{2} \times 6,100 ° F - days \times \frac{24 h}{day}}{1 \frac{{ft}^{2} ° F h}{Btu}} = 84.91 MMBtu

Heat Loss from Roof = \frac{2,750 {ft}^{2} \times 6,100 ° F - days \times \frac{24 h}{day}}{22 \frac{{ft}^{2} ° F h}{Btu}} = 18.30 MMBtu

Total heat loss from the house = 13.78 + 84.91 + 18.30 =116.99 MMBTU in a year or heating requirement is 116.99 million BTUs per year.

Calculating Wall Heat Loss Example Problems

Example #1

Please watch the following 4:58 presentation about Example #1. A house in State College, PA has 580 ft² of windows (R = 1), 1920 ft² of walls, and 2750 ft² of roof (R = 22). The walls are made up of wood siding (R = 0.81), 0.75” plywood, 3” of fiberglass insulation, 1.5” of polyurethane board, and 0.5” gypsum board. Calculate the heating requirement for the house for the heating season.

Click here for a transcript of Wall Heat Loss - Problem #1 video.

Lesson 7b, Screen 14: Calculation of Wall Heat Loss

Example 15 (formerly Example 3-14)

A house in State College, PA has 580 ft² of windows (R=1), 1920 ft² of walls, and 2750 ft² of roof (R=22). The walls are made up of wood siding (R=0.81), 0.75” plywood, 3” of fiberglass insulation, 1.5” of polyurethane board, and 0.5” gypsum board. Calculate the heating requirement for the house for the heating season.

Here in this problem, we are trying to calculate the heat loss from the entire house. Heat loss through windows, heat loss through roof, heat loss through walls and add them up. We can directly calculate heat loss through windows. Area is given as 580 ft², R-value is given as 1 and HDD for State College is 6000 degree F days (°F days). So heat loss for the season is equal to 580 ft² times 6000 °F days times 24 hours in a day divided by 1 R-value (ft² (°F hour/BTU). So we can cancel these and the heat loss through windows is 83,520,000 BTUs.

Windows

\begin{array}{l} A r e a = 580 f t^{2} \\ R = 1 \\ H D D = 6000 ° F d a y s \end{array}

Similarly, we can calculate heat loss through the roof. And area of the roof is given as 2750 ft² times 6000 °F days times 24 hours over a day divided by 22 ft² °F hour over BTU. Now, when you do this calculation, we lose about 18 million BTUs through the roof.

Heat Loss Season

\frac{{580ft}^{2} \times 6000 ° Fdays \times 24hr/day}{1 f t^{2} \times \frac{° F d a y s}{B T U}}

Heat Loss Roof

\begin{array}{l} = \frac{2750 f t^{2} \times 6000 ° F d a y s \times 24 h r / d a y s}{22 f t^{2} \times \frac{° F h r}{B T U}} \\ = 18, 000, 000 B T U s \end{array}

For the wall heat loss, we need to calculate the composite R-value because we are not given the R-value straight away, and we are given the area. So, let’s calculate the composite R-value. The first layer is wood siding, and wood siding is 0.81 in R- value and the next layer is ¾” plywood and whose R-value is 0.94. And we got 3” of fiberglass and each inch provides an R-value of 3.7 therefore 3” would be 11.10, and we have another 1 ½ of polyurethane which has 6.25 per inch R-value therefore 1.5” would provide an R-value of 9.375. At the end or inside, we have ½” drywall whose R-value is 0.45. So together, all these layers would provide an R-value of 22.7.

Wood siding = 0.81
¾ “ plywood = 0.94
3” fiberglass = 11.10
1.5” polyurethane = 9.375
.5” dry wall = 0.45
Total = 22.7

So, heat loss now can be calculated. We know the area that is 1920 ft2 given and same 6000 °F days times 24 hours per day divided by 22.67 and this comes out to be 12,119,164 BTUs.

\begin{matrix} H e a t l o s s = \frac{1920 f t^{2} \times 6000 ° F d a y s x 24 h r / d a y s}{22.67 f t^{2} \frac{° F h r}{B T U}} \\ = 12, 119, 164 B T U s \end{matrix}

So when you add all these three heat losses, the total heat loss is equal to 113,753,164 BTUs per heating season.

T o t a l H e a t L o s s = 113, 753, 164 B T U s

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [2]

Example #2

Please watch the following 9:00 presentation about Example #2. A single-story house in Anchorage, AK (HDD = 11,000) is 50 ft by 70 ft with an 8 ft high ceiling. There are six windows (R = 1) of identical size, 4 ft wide by 6 ft high. The roof is insulated to R-30. The walls consist of a layer of wood siding (R = 0.81), 2” of polyurethane board (R = 6.25 per inch), 4” of fiberglass (R = 3.70 per inch), and a layer of drywall (R = 0.45). Calculate the heat loss through the house (not counting the floor) for the season. (A good estimate for the area of the roof is 1.1 times the area of the walls, before you subtract out the area for the windows.)

Click here for a transcript of Wall Heat Loss - Problem #2 video.

Wall Heat Loss #3

Problem

[ON SCREEN TEXT]: A single-story house in Anchorage, AK (HDD = 11,000) is 50 ft by 70 ft with an 8 ft high ceiling. There are six windows (R = 1) of identical size, 4 ft wide by 6 ft high. The roof is insulated to R-30. The walls consist of a layer of wood siding (R = 0.81), 2” of polyurethane board (R = 6.25 per inch), 4” of fiberglass (R = 3.70 per inch), and a layer of drywall (R = 0.45). Calculate the heat loss through the house (not counting the floor) for the season. (A good estimate for the area of the roof is 1.1 times the area of the walls, before you subtract out the area for the windows.)

SARMA PISUPATI: OK, for this problem, 3.15. We do, more or less, the same thing as the last house, except this house is in Anchorage, Alaska, where HDD happens to be 11,000 degree days. OK. Now we have to calculate here, heat loss through windows, through walls, and through roof, to calculate the total heat loss from the house, the same way that we have done before.

Heat loss through windows. We need the area of the windows first. So area of windows equal to-- Each window is 4 feet by 6 feet. So this is 24 square feet. So we have six of them, so the total area is 144 square feet. So heat loss equal to 144 feet square times HDDs 11,000 degree days times 24 hours in a day, and divided by r value, r value happens to be 1. So 1 feet square, degrees Fahrenheit, hour over BTU.

\begin{array}{l} H D D = 11, 000 ° F d a y s \\ W i n d o w s A r e a = 4 f t^{2} \times 6 f t^{2} \\ 24 f t^{2} \times 6 = 144 f t^{2} \\ H e a t l o s s = \frac{144 f t^{2} \times 11, 000 d a y s \times 24 h r s / d a y}{1 f t^{2} ° F \frac{h r s}{B T U}} \end{array}

So you could cancel out some of these. We'll get BTUs heat loss. This is in a year. OK. So we would get this one to be approximately 38 million. 38,016,000 BTUs. This is per season or per year. OK. Now the second thing that we have to do is walls.

Here we have to calculate the area and also the r value. r value because it is a composite wall consisting of four layers. It has wood siding, which has an r value of 0.81 and 2 inches of polyurethane. And 2 times 6.25, so that is 12.5 r value. And we have a third layer, 4 inches of fiberglass. 4 inches times 3.7, that's equal to 14.8.

And then we also have 1/2 inch drywall. And we know that the drywall r value is straight away 0.45, so now the total r value of this wall happens to be 28.56. OK. Now we have to calculate the area of the walls. Area of the walls we can calculate.

Let me draw a little picture here and show you. If we have-- Let's say this is the area, and we have-- and this side is about 70, this side is 50. And we will have under there, 50 this side, and 70 this side. So total times this height is 8 feet. So the total area would be 2 times 120. 120 is 70 plus 50 times 2, because twice these values, times 8 feet is the height. So we get about 1,920 feet square.

Of course, this also has some windows, about six windows as we originally looked at, but at this point, we will take this as 1920 and subtracting windows from this. Windows is 144 feet square, so 1920 minus 144, would give us 1776 feet square.

1920 f t^{2} - 144 f t^{2} = 1776 f t^{2}

OK, so now we have to calculate the area of-- Now, if we calculate the area of 1776 feet square times 11,000 times, this is degrees Fahrenheit days, times 24 hours per day, divided by-- we have 28.56. So the heat loss, in here, comes out to be 16,416,806 BTUs per year.

\begin{matrix} Heat loss = 1776 f t^{2} \times 11, 000 ° F d a y \times 26 h r s / d a y \\ = 16, 416, 806 B T U s / y r \end{matrix}

OK, now we have to calculate roof. Roof happens to be 1.1 times the area of the walls. Area of the walls was 1920 feet square. Again, we have to take this without the windows, actual area of the walls, times 1.1, that happens to be 2112 feet square.

\begin{array}{l} R o o f = 1.1 \times 1920 f t^{2} \\ = 2112 f t^{2} \end{array}

So heat loss 2112 feet square times 11,000 times 24, divided by-- r value of this is 30-- degrees Fahrenheit, feet square, hour, over BTU. So this comes out to be 18,585,600 BTUs per year.

\begin{array}{l} Heat loss = \frac{2112 f t^{2} \times 11, 000 \times 24}{30 ° F f t^{2} \frac{h}{B T U}} \\ = 18, 585, 600 B T U s / y r \end{array}

So the total heat loss now, would be the addition of all these three together. So that is, first we have, how much? If we look at, we have 38,016,000, so 38,016,000 plus 16,416,806 plus 18,585,600, so that is equal to 73, 019,000 BTUs. So that is the total heat loss from the house.

\begin{matrix} Total heat loss = 38, 016, 000 + 16, 416, 806 + 18, 585, 600 \\ = 73, 019, 000 B T U s \end{matrix}

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [2]

Fuel Choices

Various fuels such as natural gas, electricity, fuel oil, and so on, are used to heat a house. Click on the graph below to see the percent of households that use each type of heating fuel.

Choice of Fuels by Percent of Households
Fuel Type	Percentage used
Natural Gas	49%
Electricity	34%
Fuel Oil / LPG	11%
Other	6%

Source: Department of Energy [5]

As you see, about 50 percent of the households in the United States use natural gas as their main heating fuel, and about 35 percent of the households use electricity to heat their homes. Another 11% use fuel oil, and the last 6% use something other than natural gas, electricity, and fuel oil.

Capacity and Consumption

Capacity

The amount of heat a furnace can deliver is called its capacity. Heating units are manufactured and sold by their capacity. The heating capacities of Natural Gas, Propane and Fuel Oil are measured according to BTU/h, and the capacity of Electricity is measured in kilowatts.

Consumption

The amount of energy a furnace actually uses is called consumption. In other words, we pay monthly bills for the consumption of a particular heating fuel. Heating Fuels are sold to consumers in different units of measure. For example, Natural gas is sold by cubic feet (ft³).

Press play to see the difference between capacity and consumption in a gas-heated home. (36 seconds)

Click for a description of the animation.

The animation shows the capacity of the gas heater in BTUs per hour and a meter showing the consumption of fuel in cubic feet.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [2]

Fuel Comparison

Capacity, consumption, and other information about various types of fuel
Fuel	Capacity	Consumption	Additional Information
Natural Gas	Measured in British thermal units per hour (BTU/h). Most heating appliances for home use have heating capacities of between 40,000 and 150,000 BTU/h. In the past, gas furnaces were often rated only on heat input; today the heat output is given.	Consumption of natural gas is measured in cubic feet (ft³). This is the amount that the gas meter registers and the amount that the gas utility records when a reading is taken. One cubic foot of natural gas contains about 1,000 BTU of energy.	Utility companies often bill customers for CCF (100 cu. ft) or therms of gas used: one therm equals 100,000 BTUs. Some companies also use a unit of MCF, which is equal to 1,000 cu. ft One MCF equals 1,000,000 BTUs (1 MM BTUs).
Propane or Liquefied Petroleum Gas (LPG)	Measured according to BTU/h.	Consumption of propane is usually measured in gallons; propane has an energy content of about 91.300 BTUs per gallon.	Can be used in many of the same types of equipment as natural gas. It is stored as a liquid in a tank at the house, so it can be used anywhere, even in areas where natural gas hookups are not available.
Fuel Oil	The heating (bonnet) capacity of oil heating appliances is the steady-state heat output of the furnace, measured in BTU/h. Typical oil-fired central heating appliances sold for home use today have heating capacities of between 56,000 and 150,000 BTU/h.	Oil use is generally billed by the gallon. One gallon of #2 fuel oil contains about 140,000 BTU of potential heat energy.	Several grades of fuel oil are produced by the petroleum industry, but only #2 fuel oil is commonly used for home heating.
Electricity	The heating capacity of electric systems is usually expressed in kilowatts (kW); 1 kW equals 1,000 W. A kilowatt-hour (kWh) is the amount of electrical energy supplied by 1 kW of power over a 1-hour period. Electric systems come in a wide range of capacities, generally from 10 kW to 50 kW.	Electricity is sold in kWh (kilowatts per hour).	The watt (W) is the basic unit of measurement of electric power.

Heating Values of various fuels

Each unit of fuel when burned gives different amounts of energy. The energy that is released when a unit amount of fuel is burned is called the heating value. The heating value of a fuel is determined under a standard set of conditions. A comparison of approximate heating values of various fuels is shown in the table below.

Heating values of commonly used heating fuels
Fuel	Unit	Heating Value (BTU's)
Natural Gas	CCF (100 Cu. ft) or Therm	100,000
Natural Gas	MCF (1,000 Cu.ft)	1,000,000
Fuel Oil	Gallon	140,000
Electricity	kWh	3,412
Propane	Gallon	91,300
Bituminous Coal	Ton	23,000,000
Anthracite Coal	Ton	26,000,000
Hardwood	Cord	24,000,000

From the table above, it should be noted that if a gallon of fuel oil is burned, one would get 140,000 BTUs. Similarly, a CCF of natural gas would fetch 100,000 BTUs.

Heating Efficiency

An assumption is made here that all the energy from the fuel is released, and all the heat is available to heat the place. However, generally, when a fuel is burned in a furnace, not all the energy (heat) is available for the final end user.

The energy efficiency of a furnace is not 100 percent. Not all the energy from the fuel is released, and not all the heat is available to heat the place. For example, if a furnace’s efficiency is, say, 50 percent, then twice as much fuel would be needed to heat a home.

Looking again at the table on the previous screen, we saw that the heating value of fuel oil is given as 140,000 BTUs. However, if the furnace’s efficiency is 50 percent, then the actual heating value of fuel oil is 140,000 BTUs x 0.5 (efficiency) = 70,000 BTUs. In other words, when a gallon of oil is burned, 70,000 BTUs of heat is actually available to the user.

Heating values of commonly used heating fuels if efficiency = 50 %
Fuel	Unit	Heating Value (BTU's)	If Efficiency = 50 %
Natural Gas	CCF (100 Cu. ft) or Therm	100,000	50,000
Natural Gas	MCF (1,000 Cu.ft)	1,000,000	500,000
Fuel Oil	Gallon	140,000	70,000
Electricity	kWh	3,412	1706
Propane	Gallon	91,300	45,650
Bituminous Coal	Ton	23,000,000	11,500,000
Anthracite Coal	Ton	26,000,000	13,000,000
Hardwood	Cord	24,000,000	12,000,000

Efficiency of a Furnace

Click here to see the graph's tabular data

Efficiency of a Furnace

The table below contains the data from a line plot showing the efficiency of a furnace. The percent efficiency is dependent on the heating value of fuel oil (measured in BTU) and shows a strong positive correlation.

Efficiency of a Furnace
Efficiency of a Furnace	Heating Value of Fuel Oil (BTUs)
50%	70000
55%	77000
60%	84000
65%	90000
70%	100000
75%	105000
80%	111000
85%	122000
90%	125000
95%	131000
100%	140000

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [2]

It can be clearly seen that as the efficiency of the furnace increases, the amount of heat available increases proportionally.

The higher the efficiency, the less oil needs to be put into the furnace to get the same amount of heat output.

Most of the heating furnaces burn fuel and release hot combustion gases. The hot combustion gases heat the incoming cold air and go out through the chimney. In older furnaces, all the heat in the fuel is not released or not transferred to the cold air (or water, in the case of heat registers and water heaters), and therefore is lost through the chimney. The air or water that is heated distributes the heat throughout the house. Newer models of furnaces have gotten better at getting more of the heat into the cold air and, therefore, into your house.

Click the play button and observe how a wood burning furnace operates at 75% efficiency.

Click here to open a text description of How a Wood Furnace Operates

How a Wood Burning Furnace Operates

Cold combustion air from outside is pulled into the furnace combustion chamber by an electric blower. The wood fire in the chamber heats the air to 1 million BTUs. The hot combustion gasses heat the cold, outside air to 750,000 BTUs, which will circulate through the house. The combustion gasses (250,000 BTUs) travel out through the chimney.

Furnaces are usually not as efficient when they are first firing up as they are running at steady-state. It is sort of like a car getting better mileage in steady highway driving than in stop-and-go city traffic.

What matters over the course of the year is the total useful heat the furnace delivers to your house versus the heat value of the fuel it consumes. This is kind of like measuring the gas mileage your car gets by asking how many miles you drove this year and dividing it by how many gallons of gas you bought.

For furnaces, they call this measure the AFUE (Annual Fuel Utilization Efficiency). The federal minimum-efficiency standards for furnaces and boilers took effect in 1992, requiring that new furnace units have an AFUE of at least 78 percent and new boiler units have an AFUE of at least 80 percent. In comparison, many old furnaces and boilers have AFUE ratings of only 55 to 65 percent.

To find out how efficient your furnace is, look for an energy guide label like this:

Energy Guide Label.

Credit: Union Gas: Wise Energy Guide [6]

The table below gives the efficiencies of most efficient furnaces that were available in 2002–2003.

Efficiency range of some of the most efficient furnaces in 2002–2003
Fuel	Furnace Type	Efficiencies (%)
Natural Gas	Hot air	93.0 - 96.6
Natural Gas	Hot Water	83.0 - 95.0
Natural Gas	Steam	81.0 - 82.7
Fuel Oil	Furnace	83.8 - 86.3
Fuel Oil	Hot Water	86.0 - 87.6
Fuel Oil	Steam	82.5 - 86.0

When buying a new furnace, make sure its heating capacity (output) is appropriate for your home. If the insulation and/or windows in your home have been upgraded since the old heating equipment was installed, you can probably use a much less powerful furnace or boiler. Oversized furnaces operate less efficiently because they cycle on and off more frequently; in addition, larger furnaces are more expensive to buy.

Energy Costs

It is clear now that when a unit of fuel is burned not all of it is available to the end user, and that as the furnace efficiency increases, higher amounts of heat will be available. An important question that needs to be addressed is how much it costs to buy the energy or heat to heat a place.

Fuel is usually sold in gallons or CCF or kWh. Comparing the actual cost of energy to produce a certain amount of heat for the end user would be easy if the comparison is made on an energy basis rather than on a unit basis. That is, \$/BTUs rather than \$/gal or CCF or kWh.

We can use the following formula to calculate Actual Energy Cost:

$A c t u a l E n e r g y C o s t = \frac{F u e l C o s t (\frac{$}{U n i t o f F u e l})}{H e a t i n g V a l u e (\frac{M M B T U s}{U n i t o f F u e l}) \times E f f i c i e n c y}$

Example

Let’s say we need one million BTUs to keep a place warm at a certain temperature. What would it cost to get those million BTUs from oil or gas or electricity? Let’s assume that:

Cost, efficiency, and heating value of different materials
Material	Cost per unit	Efficiency	Heating Value
Natural Gas	$6.60/MCF	90%	1,000,000 BTUs or 1.0 MM BTU/MCF
Oil	$1.25/Gallon	85%	140,000 BTUs or 0.14 MM BTUs/Gallon
Electricity	$0.082/kWh	97%	3,412 BTUs or .003412 MM BTUs/kWh

Using the formula below, we can calculate the Actual Energy Cost.

$Actual Energy Cost = \frac{Fuel Cost (\frac{$}{Unit of Fuel})}{HeatingValue (\frac{MMBtus}{Unit of Fuel}) ×Efficiency}$

$Oil(in central heating system) cost = \frac{\frac{$ 1.25}{G a l}}{\frac{0.14 M M B t u s}{G a l} \times 0.85 (Efficiency)} = $ 10.50 / M M B t u$

$Electrical Resistance Heat Cost = \frac{\frac{$ 0.082}{k W h}}{\frac{0.003412 M M B t u s}{k W h} \times 0.97 (Efficiency)} = $ 24.77 / M M B t u s$

Energy Cost Examples

Example 1

Please watch the following 1:26 presentation about Example #1. Your old oil furnace runs at about 68% efficiency. If you buy your oil for $1.02/gal, calculate your actual cost on an MM BTU basis.

Click here to open a transcript of the Energy Cost Example #1

Energy Cost Example #1

Your old oil furnace runs at about 68% efficiency. If you buy your oil for $1.02/gal, calculate your actual cost on an MM BTU basis.

Ok, the old furnace runs at about 68% efficiency in this problem. This is 5.6 and the old furnace runs at an efficiency of E=0.68, and we have the actual cost per unit price or unit fuel which is $1.02 per gallon. And we also know the calorific value or heating value in millions of BTUs. When you burn one gallon of oil, we get .13 million BTUs so we apply the same formula to get the actual cost. Which is cost per unit fuel which is $1.02/gallon divided by the heating value which is 0.13 MMBTUs per gallon. We have to have the same units here. And times the efficiency here. Efficiency is 0.68. Gallons and Gallons are canceled, and we get this one as $11.50 / Million BTUs.

\begin{array}{l} E = 0 .68 \\ Fuel = $1 .02/gal \\ 1 Gal = 0 .13 MMBTUs \\ = \frac{$1 .02/gal}{0 .13 MMBTUs/gal \times 0 .68} \\ = \frac{$11 .50}{MMBTUs} \end{array}

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [2]

Example 2

Please watch the following 2:44 presentation about Example #2. Natural gas costs 9.74 dollars/MCF. Heating oil costs 0.99 cents/gal. The natural gas furnace runs at 90% efficiency and the oil furnace runs at 80% efficiency. Which fuel is cheaper?

Click here to open a transcript of the Energy Cost Example #2

Energy Cost Example #2

Natural gas costs $9.74/MCF. Heating oil costs $0.99/gal. The natural gas furnace runs at 90% efficiency and the oil furnace runs at 80% efficiency. Which fuel is cheaper?

Ok. This 5.7 is an interesting problem here. We are trying to compare the prices of two fuels – Natural Gas which sells for $9.74/MCF, and we also have oil that sells at $0.99/gallon. We are trying to compare the prices of these two and choose which one is the best fuel or cheapest fuel. So we need to calculate the price per million BTUs so that we can compare these two fuels. And we also know the furnace efficiencies of each of these. Natural gas furnace efficiency is 0.9, and we know the oil furnace efficiency is 0.8; it is given. So we need to calculate the actual cost and compare the cost.

Natural gas actual cost will be cost per unit fuel, which is $9.74/MCF divided by the heating value per unit fuel. Heating value for this one happens to be 1.0 Million BTUs per MCF, and we have to multiply by the efficiency here in the denominator which is 0.9, so the Natural Gas price turns out to be $10.83 or $10.83 per Million BTUs (MMBTUs).

\begin{array}{l} Natural Gas \frac{$9 .74}{MCF} \\ 0 .9 efficiency \\ Natural Gas = \frac{\frac{$9 .74}{MCF}}{\frac{1 .0 MMBTU}{MCF \times 0 .9}} \\ = \frac{$10 .82}{MMBTUs} \end{array}

When you do similar calculation for oil here, the actual price is, per unit is $0.99 per gallon here and how many million BTUs do we get per gallon? 0.13 Million BTUs (0.13 MMBTUs). We have done this before. We have to have the same units here. Gallons and gallons and MCF and MCF here in this case (natural gas) and times the efficiency is 0.8. So the price works out to be $9.50 per Million BTUs. Same million BTUs would cost $10.82 for Natural Gas and oil would be $9.50, so oil is cheaper.

Annual Heating Costs

In the example on the page 12, we see that the heat loss from the house (walls, windows, and the roof) was 116.53 MM BTUs. We also know that it costs $24.77 for 1MM BTUs if electrical resistance heating is used (see Example 17 on page 26). The total cost for the heating can be calculated as follows:

$C o s t o f H e a t i n g = (116.53 M M B T U s) \times \frac{$ 24.77}{M M B T U s} = $ 2, 886.44$

The price of fuel oil is $10.50 per MMBtu. The annual heating cost would be:

$C o s t o f H e a t i n g = (116.53 M M B T U s) \times \frac{$ 10.50}{M M B T U s} = $ 1, 1223.57$

Example

A house in International Falls, MN (HDD = 10,500) consists of 1248 ft² of walls with an R-value of 13 and 1150 ft² of roof with an R value of 29. The home is heated with natural gas. The AFUE is 0.90 and the price of natural gas is $0.88/CCF. What is the annual heating cost?

Energy cost per million BTUs from natural gas can be calculated using the following equation.

A c t u a l E n e r g y C o s t = \frac{F u e l C o s t (\frac{$}{U n i t o f F u e l})}{H e a t i n g V a l u e (\frac{M M B T U s}{U n i t o f F u e l}) \times E f f i c i e n c y}

$Actual Energy Cost = \frac{\frac{$ 0.88}{C C F}}{\frac{0.1 M M B t u s}{C C F} \times 0.90 (Efficiency)} = $ 9.80 / M M B t u$

Heat required can be calculated from the heat loss. Heat loss from the house is from two sources: walls and the roof. Heat loss from each of these sources for a year (season) can be calculated by using the following equation.

$Heat Loss from Walls = \frac{1, 248 f t^{2} \times 10, 500^{o} f - d a y s \times \frac{24 h}{d a y}}{13.0 \frac{f t^{2}^{o} f h}{B t u}} = 24.19 M M B t u$

$Heat Loss from Roof = \frac{1, 150 f t^{2} \times 10, 500^{o} f - d a y s \times \frac{24 h}{d a y}}{29.0 \frac{f t^{2}^{o} f h}{B t u}} = 9.99 M M B t u$

Total heat loss = sum of heat loss from the walls and the roof

= 24.19 + 9.99 = 34.18 M M B T U s

Annual heating cost = Annual heat loss (MMBTUs) x Actual energy cost ($/MMBTU)

$= (34.18 M M B t u s) \times \frac{$ 9.80}{M M B t u s} = $ 334.96$

Annual Heating Cost Examples

Example 1

Please watch the following 6:01 presentation about Example Problem #1. A house in Bismark, ND (HDD = 9,000) has 860 ft²of windows (R = 1), 2,920 ft² of walls (R = 19), and 3,850 ft² of roof (R = 22). Calculate how much heating oil is required to heat this house for the heating season. The furnace efficiency is 80%.

Click here to open a text description of the Annual Heating Cost Example 1.

Annual Heating Cost Example 1

A house in Bismark, ND (HDD = 9000) has 860 ft² of windows (R = 1), 2920 ft² of walls (R = 19), and 3850 ft² of roof (R = 22). Calculate how much heating oil is required to heat this house for the heating season. The furnace efficiency is 80%.

Ok, this problem is very similar to what we have done before. Which is calculating the heat loss from various surfaces and adding all of those to get the total heat loss from the house. And to calculate the oil requirement based on the furnace efficiency. The house is located in Bismark, ND and HDD there is given as 9,000, so HDD is given. This HDD remains the same for all different surfaces. And we also know the surfaces of each of these components, like windows. Let’s do the calculation first for windows.

Windows area is given as 860 square ft, and we also know the R-value of this. R-value is given as 1 – this is ft °F h/BTUs. So we can calculate heat loss through windows. Where all we need is the area, 860 square ft times HDD which is 9,000 in this case times 24 hours in a day divided by, we get the R-value here. That is 1 ft°F h/BTU. So ft/ ft cancel, °F/°F, 24 hours/24 hours, days and days, so the total heat loss through windows is the number that we get here. It happens to be 185,760,000 BTUs.

\begin{array}{l} {Windows = 860 ft}^{2} \\ {R-value = 1 ft}^{2} ° F h / BTUs \\ Heat Loss = \frac{{860 ft}^{2} \times {9,000 ft}^{2} ° F day \times 24 hrs/day}{{1 ft}^{2} ° F h / BTUs} \\ = 185,760,000 BTUs \end{array}

Similarly, we can calculate the heat loss - this is through windows. We can calculate heat loss through the walls. Wall area is 2,920 ft² times 9,000 °F days times 24 hours per day divided by R-value of 19 for walls. And we can cancel out the units and make sure that everything makes sense and this turns out to be 33,195,789 BTUs.

\begin{array}{l} Heat Loss = \frac{{2,920 ft}^{2} \times {9,000 ft}^{2} ° F day \times 24 hrs/day}{{19 ft}^{2} ° F h / BTUs} \\ = 33,195,789 BTUs \end{array}

Now heat loss through the roof. You can calculate it again separately and the area of the roof happens to be 3850 ft², and 9,000 degree days times 24 hours over a day divided by, the roof generally has higher R-value, 22 ft² °F h/BTUs, ok? Now let’s cancel out these units and the heat loss is to be 37,800,000 BTUs. So the total heat loss is the sum of all these three and when you add these up you get 256,755,789 BTUs.

Heat Loss = 256,755,789 BTUs

Now, the furnace efficiency is given, and we are using, in this case, heating oil. Heating oil is 130,000 BTUs so how much is required? How much heating oil is required? We need 256,755,789 BTUs. When we buy heating oil, we get 130,000 BTUs per every gallon, and although we get 130,000, this is theoretical, the efficiency is given as 0.8 so only 80% will get really available as heat. So, that makes it, actually, the requirement a little bit higher, so that is equal to now, if we do this calculation, it will be 2,468.8 gallons or roughly 2,469 gallons of oil is required to heat this place.

\frac{256,755,789 BTUs}{130,000 BTUs / gal \times 0 .8} = 2,468 .8 gallons or 2,469 gallons

Pay Back Period

Earlier sections illustrated that adding more insulation and improving the R-value of a wall would help in cutting heat loss. Less heat loss reduces the amount of fuel that needs to be burned, thereby reducing the heating costs and protecting the environment. However, adding insulation often involves additional investment.

The money invested into insulation can be recovered or paid back using the money saved because of the reduction of fuel usage. The time it takes to recover the additional cost through savings is called the pay-back period. A simple pay back is the initial investment divided by annual savings after taxes.

A simple calculation illustrates this term. If the R-value of the wall used in an earlier example is improved to R-23 by adding additional insulation, which costs $254, the heat loss can be reduced. The new heat loss after improvement can be calculated using the equation below.

$New Heat Loss from Walls = \frac{1, 248 f t^{2} \times 10, 500^{o} F - days \times \frac{24 h}{d a y}}{23.0 \frac{f t^{2}^{o} F h}{B t u}} = \frac{13.7 M M B t u}{Y e a r}$

Heat loss from the roof remains the same and is equal to 9.99 MM BTUs. Therefore, new annual total heat loss is only 13.7 + 9.99 =23.69 MM BTUs. The annual cost of heating after this improvement would be:

$= (23.69 M M B t u s) \times \frac{$ 9.80}{M M B t u s} = $ 232.16$

The savings is $334.96 - $232.16 = $102.80 every year. Remember that to get this savings, an investment of $254 was made. So if this investment was paid off by the savings, it would take

$\frac{$ 254.00}{$ 102.80 / y e a r} = 2.47 y e a r s$

The pay-back period is 2.47 years. Shorter pay-back periods indicate that the additional investment can be paid off quickly and the homeowner can start saving money after that.

The formula below will help you to estimate the cost effectiveness of adding insulation in terms of the "years to payback" for savings in heating costs.

$Y e a r s t o P a y b a c k = \frac{C_{i} \times R_{1} \times R_{2} \times E}{C_{e} \times (R_{2} - R_{1}) \times H D D \times 24}$

Where:

C_i = Cost of insulation in $/square feet. Collect insulation cost information; include labor, equipment, and vapor barrier if needed.

C_e = Cost of energy, expressed in $/BTUs. To calculate this, divide the actual price you pay per gallon of oil, kilowatt-hour (kWh) of electricity, gallon of propane, or therm (or per one hundred cubic feet [CCF]) of natural gas by the BTU content per unit of fuel.

E = Efficiency of the heating system. For gas, propane, and fuel oil systems, this is the Annual Fuel Utilization Efficiency, or AFUE.

R₁ = Initial R-value of section

R₂ = Final R-value of section

R₂ – R₁ = R-value of additional insulation being considered

HDD = Heating degree days/year. This information can usually be obtained from your local weather station, utility, or oil dealer.

24 = Multiplier used to convert HDD to heating hours (24 hours/day).

The formula above works only for uniform sections of the home. For example, you can estimate years to pay back for a wall or several walls that have the same R-values, if you add the same amount of insulation everywhere. Ceilings, walls, or sections of walls with different R-values must be figured separately.

Example

Mr. Energy Conscious (who lives in East Lansing, MI with an HDD of 7,164) wants to know how many years it will take to recover the cost of installing additional insulation in his attic. He renovated his attic and increased the level of insulation from R-19 to R-30 by adding additional insulation. He has a gas furnace with an AFUE of 0.88 and pays $0.95/CCF for natural gas. The attic insulation costs $340 to cover 1,100 sq. ft.

The pay-back period is given by the equation 5.5:

Y e a r s t o P a y b a c k = \frac{C_{i} \times R_{1} \times R_{2} \times E}{C_{e} \times (R_{2} - R_{1}) \times H D D \times 24}

R₁ = 19; R₂ = 30; and R₂- R₁ = 30 - 19 = 11

HDD = 7,164 and E = 0.88

The most important part of this problem is to determine the cost of insulation per one sq. ft (C_i) and cost of energy per one BTU (C_e).

C_{i} = \frac{$ 340}{1, 100 s q . f t .} = $ 0.31 / s q . f t .

$A n d, C_{e} = \frac{$ 0.95}{1 C C F \times \frac{100, 000 B t u s}{1 C C F}} = $ 0.0000095 / B t u$

Note: The cost for one BTU is a very small number.

Substituting the values in the equation,

Y e a r s t o P a y b a c k = \frac{0.31 \times 19 \times 30 \times 0.88}{0.0000095 \times [11] \times 7, 164 \times 24} = 8.65 y e a r s

After 8.65 years, Mr. Energy Conscious can start saving money for himself for the rest of the period that he lives in that home. During the entire period the energy that he is not using can help the environment.

Pay Back Period Examples

Example 1

Please watch the following 3:04 presentation about Example Problem #1. For a house in Hackensack, NJ (HDD = 4,600), the installed cost to upgrade from R-13 to R-22 is $0.60/ft². The AFUE for the oil furnace is 0.78 and heating oil costs $1.13/gal. How long will it take to recover the initial investment?

Click here to open a transcript of the Payback Period Example Problem #1.

Payback Period Example 1

For a house in Hackensack, NJ (HDD = 4,600), the installed cost to upgrade from R-13 to R-22 is $0.60/ft². The AFUE for the oil furnace is 0.78 and heating oil costs $1.13/gal. How long will it take to recover the initial investment?

Ok, this is 5.10. Heating Degree Days are given. In this problem, basically we are trying to calculate the pay back period again using the formula that we have. That we derived basically and payback period for adding insulation is cost of insulation times R₁ times R₂ times efficiency divided by cost of energy times the difference in R-value times HDD times 24. That is the formula that we need to use.

Payback = \frac{C_{i} \times R_{1} \times R_{2} \times E}{C_{e} \times [R_{2} - R_{1}] \times HDD \times 24}

We have all the data. HDD is given as 4,600 and cost of insulation C_i is given as $0.60 per ft² and the efficiency of the furnace is given as 78% or 0.78. We know the initial R-value, R₁ = 13, and we know the final R-value; the improved R-value which is 22, the difference is 9. And we know the price of energy or cost of energy. We are paying $1.13 to buy a gallon of oil and when we buy a gallon of oil by paying $1.13 we get 130,000 BTUs.

\begin{array}{l} HDD = 4,600 ° F days \\ C_{i} = $0 {.61 / ft}^{2} \\ E = 0 .78 \\ R_{1} = 13 \\ R_{2} = 22 \\ {Difference = R}_{2} - R_{1} = 9 \\ Cost of oil = $1 .13/gal \\ \frac{$1 .13}{130,000 BTUs} = $0 .0000869 per BTU \end{array}

So, for every BTU we pay $0.0000869. So we can use the formula now. It consists of C_i, C_i is cost of insulation, which is 0.06 per ft², dollars per ft² times R₁ which is 13, again units, you have to make sure ft², °F, hr/BTU. And here R₂ is 22 and times the efficiency which is .78 divided by the cost of energy which is dollars per BTUs. $0.0000869/1 single BTU times the difference between these two R values here and that is 22 minus 13 (9) times days, (HDD) 4,600 times 24 and when you do this calculation it turns out to be 15.5 years is the payback period.

\begin{array}{l} = \frac{$0 {.60/ft}^{2} \times 13   22 \times 0 .78}{$0 .0000869 / BTU \times 9 \times 4,600 \times 24} \\ Payback Period = 15 .5 years \end{array}

Example 2

Please watch the following 4:10 presentation about Example Problem #2. Lt. Dave Rajakovich has 1200 ft² of roof in his home in Pittsburgh, PA (HDD = 6,000). He is considering upgrading the insulation from R-16 to R-22. The estimate from the contractor was $775. His home is heated with natural gas. Last year, the average price he paid for natural gas was $9.86/MCF. Assuming an AFUE of 86%, how long will it take Dave to recover his investment?

Click here to open a text description of the Payback Period Example Problem #2.

Payback Period Example #2

Lt. Dave Rajakovich has 1200 ft² of roof in his home in Pittsburgh, PA (HDD = 6,000). He is considering upgrading the insulation from R-16 to R-22. The estimate from the contractor was $775. His home is heated with natural gas. Last year, the average price he paid for natural gas was $9.86/MCF. Assuming an AFUE of 86%, how long will it take Dave to recover his investment?

Ok, this is 5.11. Here Dave has a house, and he is trying to improve the insulation and the contractor comes up with an estimate of $775. He is using natural gas to heat the home, and we are trying to calculate how long will it take Dave to recover his investment? And this is a typical problem that uses an equation for payback period. Equal to C_i, cost of insulation, times R₁ times R₂ times efficiency divided by cost of energy times again R₂ minus R₁, this is the final R-value minus the initial R-value times HDD times 24.

Payback = \frac{C_{i} \times R_{1} \times R_{2} \times E}{C_{e} \times [R_{2} - R_{1}] \times HDD \times 24}

Do we have all the pieces of information for this formula?

Cost of insulation: Cost of insulation should be in dollars per square foot. So Dave has got an estimate of $775 to cover an area of 1200 square foot. Roof area happens to be 1200 ft². To cover this area with insulation it costs $775, so we can calculate the cost per ft. This happens to be $0.65 per ft². That’s what we want, per ft².

Do we know R₁? Yes we know, R₁ is equal to 16, R₂ is equal to 22 and the furnace efficiency, E, is equal to 0.86. And we also know HDD. HDD is 6,000, and we know 24 hours.

\begin{array}{l} \frac{$775}{{1,200 ft}^{2}} = $0 {.65 / ft}^{2} \\ R1 = 16 \\ R2 = 22 \\ E = 0 .86 \\ HDD = 6,000 \end{array}

Only thing here is we need to calculate the cost, C_e, cost of energy. And we are paying here, or Dave is paying $9.86 per MCF. Remember, MCF is basically one million BTUs. So the price would be $9.86 per million BTUs. So this will be equal to 0.00000986.

\begin{array}{l} C_{e} = $9 .86 / MCF = 9 .86 / 1,000,000 BTUs \\ = 0 .00000986 \end{array}

And if we plug this into this number here, into this formula here, 0.65 times 16 times 22 times 0.86 and divided by this is 0.00000986 and R₂ – R₁ happens to be 6 and 6,000 is the degree days and 24. This should come out to be, I guess 23 years roughly. This is kind of a long time period to recover the investment.

\begin{array}{l} = \frac{0 .65 \times 16 \times 22 \times 0 .86}{$0 .00 00986 \times 6 \times 6,000 \times 24} \\ Payback Period = 23 years \end{array}