So far, we have assumed that minimum rate of return is fixed over the life of the project. But there are situations where other opportunities for investment (that determine the minimum rate of return) can make different rate of returns in different time. Thus, minimum rate of return can change over time. For example, other opportunities for investment of capital can give i*=12% now; and three years from now, we might expect a project that has a return on investment of i*=15%.
For analyses with minimum rate of return that change with time, NPV and PVR are recommended as the best methods. ROR is not a reliable approach for such analyses.
Example 4-5:
Cash flows for two mutually exclusive investment projects A and B are given as:
| C=$40 | I=$20 | I=$20 | I=$20 | I=$20 | I=$20 | L=$40 | |
| A) |
|
||||||
| 0 | 1 | 2 | 3 | ... | 10 | ||
| C=$50 | I=$25 | I=$25 | I=$25 | I=$25 | I=$25 | L=$50 | |
| B) |
|
||||||
| 0 | 1 | 2 | 3 | ... | 10 | ||
C: Cost, I:Income, L:Salvage
Analyze these alternatives, assuming the minimum rate of return for the first and second years is 25% and for third to tenth year it is 15%.
Results indicate that project B is a better economic investment.
Note:
After year 2, minimum rate of return changes from 25% to 15%. In order to calculate the NPV of the cash flow, we have to separate the payments that happened at and before year 2 from payments that occurred after year 2.
Payments at year 2 and before that are not going to be affected by the change:
PV of payments from year 0 to year 2:
Project A: Present value of year 0 to year 2 payments
Project B: Present value of year 0 to year 2 payments
But payments after year 2 will be affected by the change.
To calculate the NPV of those payments and apply the change in i, first, we need to discount all the payments occurred after year 2 to this year (we set the year 2 as the base year) by i* = 15% and we calculate value of all payments at year 2:
Project A: Value of year 3 to year 10 payments at year 2
Project B: Value of year 3 to year 10 payments at year 2
Second, we discount the year 2 values for 2 years by i* = 25%to get the present value (value at year 0) of the payments:
Project A: Present Value of year 3 to year 10 payments
Project B: Present Value of year 3 to year 10 payments
In the end, we add all the values together:
Another Method:
You can also treat each payment separately. This method is especially helpful when payments are not equal or when you are using spreadsheet to calculate the NPV.
We separate the payments that happened at and before year 2 from payments after year 2. Payments at and before year 2 will be discounted just by 25%:
PV of payments from year 0 to year 2:
Project A: PV year 0 to year 2
Project B: PV year 0 to year 2
For payments after year 2, first we calculate their value at year 2:
Project A: Value of year 3 to year 10 payments at year 2
Project B: Value of year 3 to year 10 payments at year 2
Second step, we discount the year 2 values for 2 years by i* = 25% to get the present value (value at year 0) of the payments:
Project A: Present Value of year 3 to year 10 payments
Project B: Present Value of year 3 to year 10 payments
In the end we add all the values together:
Microsoft Excel or Spreadsheet
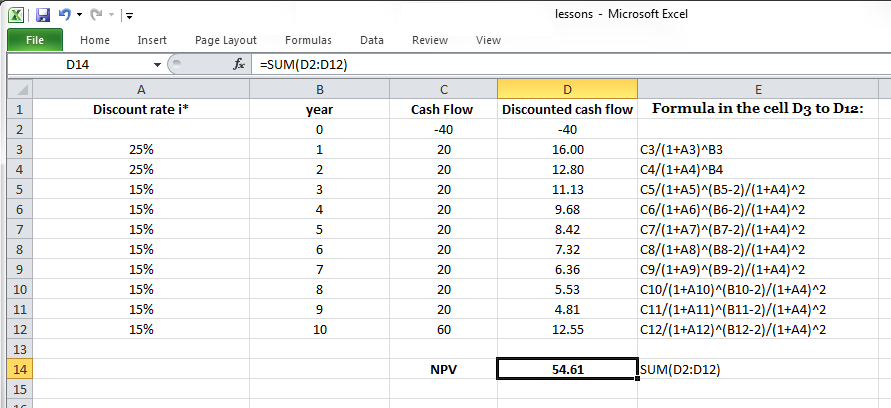
If you are using Microsoft Excel or another spreadsheet to calculate the Net Present Value for the cash flow that has different discount rates over the life of project, be careful! You can not use the NPV function. However, you can calculate the Net Present Value by making a summation over calculated discounted cash flow. Figure 4-3 displays how Net Present Value for Project A cash flow with a changing minimum rate of return can be calculated. Note the formula in the cell D3 to D12.
PRESENTER: So far, we assume the minimum rate of return in our analysis is fixed over the lifetime of the project. And it's not changing over time. But there are situations that we might have other opportunities for investment later on in the following years. So our minimum rate of return might change.
And it means that the discount rate, the minimum discount rate that we are using in our analysis will change too. In this video, I'm going to explain how we can evaluate the mutually exclusive projects or, in general, any other project if the minimum rate of return, if the discount rate changes over the lifetime of a project. So if the minimum rate of return changes with the time, the NPV and PVR present value ratio are recommended as the best methods. And rate of return is not a reliable approach for the project evaluation.
Let's work on this example. We have the cash flow for Project A and Project B that are mutually exclusive. And we assume the minimum rate of return for the first and second year is 25%. And the minimum rate of return changes to 15% from year 3 to year 10. So the first thing that we have to do is to separate the payments before the change and after the change.
So here, minimum rate of return changes after year 2. So I draw this red vertical line here to separate the payments before this year and payments that are after year 2. Return of present value of 40. Present value of these 20 payments at year 1 and 2. So present value of 40 is $40. And it is negative because it's a cost, it's an investment, and it's happening at present time. So there is no discounting needed here.
But two payments. We have two payments of $20 at year 1 and year 2. We discount them on 25%. And there are two of them. And then we need to calculate the present value of payments that are happening after year 2.
These payments are going to be affected by the change in the minimum rate of return. So first, we need to calculate the present value of these payments at 15% rate of return through the year 2 and then after discount at present value for 2 years with 25% of discount rate. So here, we have 8 payments of $20.
So we discount them 20 year 2 by the 15%. And then after, we discount that by 25% for 2 years. That is going to give us the present value here. And for the salvage value, it's the same. We discount the salvage value for 8 years at 15% and then we discount that after 2 years by 25%.
So we use this method to calculate the present value, net present value, NPV, for two mutually exclusive projects. And as we can see here, Project B has higher net present value. So I'm going to show you how we can calculate this in Excel using the other method, calculating the present value of each payment, and then add them back together. So I have the cash flow of Project A here, cash flow of Project B, and I wrote the minimum rate of return here for each year.
So as we can see here, we have 25% for year 1 and 2. And we have 15% from year 3 to year 10. So cash flow of Project A, cash flow of Project B. And for the last year, I added the salvage to the annual payment of the last year. So Project A, I'm going to calculate the present value of each payment in this cell.
So present value of these $40 of investment is going to be the same as $40. It doesn't need to be discounted because it is happening at the year 0. So present value of the $20. So I write equal sign at $20 divided by 1 plus interest rate, power, the year. So this is not going to be affected by change in the minimum rate of return.
So these 2 years are the same, so I just apply this equation to for the year 2. But for the year 3, how do we calculate the present value of this $20 that is happening at year 3? So it is going to be affected by two interest rates. 20 divided by open parentheses, 1 plus 15% power. So this needs to be discounted for 1 year because minimum rate of return changes at year 2. And this payment is 1 year away from year 2.
So I write year 1. And again, I have to divide that. I have to discount that by 2 years because this is going to give me the present value of this $20 here. And then I need to discount that at the rate of 25% for 2 more years. So 1 plus 25% power 2. And this is the same for the rest. So in order to apply these to the other cells, I will just write for this.
So read the year from here and minus 2, which is the year that the minimum rate of return changes. And I apply this to the other cash flow. And the same for Project B. Investment at present time as the same for year 1. It equals 1 plus 25% power the year.
For year 1 and year 2, there are similar. For year 3, this is 25 divided by open parentheses 1 plus 15% interest rate power year minus 2. And again, this divided by 1 plus 25% power 2.
And I apply this to the end. So these two should give me the present value. And I calculate the NPV for Project A, NPV for Project B. NPV for Project A equals the summation of all these present values. And the same for B.