3.8. The Air Mass used in Engineering Testing

For the good of the engineering community, air masses were "fixed" in 1976 as the U.S. Standard Atmosphere for the ideal clear sky atmosphere in the mid-latitudes of the USA. Yep, and nothing has changed since 1976, right? (cough)

Actually, the American Society for Testing and Materials (ASTM) developed the "Terrestrial Reference Spectra for Photovoltaic Performance Evaluation" so that we could compare and evaluate the performance of our solar technologies, like PV cells and modules. The full documentation of the reference standard is held by the National Renewable Energy Laboratory (NREL AM Standard).

The specified atmospheric conditions are:

1. "1976 U.S. Standard Atmosphere" with temperature, pressure, aerosol density (rural aerosol loading), air density, molecular species density specified in 33 layers;
2. Absolute air mass of 1.5 (solar zenith angle 48.19°s);
3. Angstrom turbidity (base e) at 500 nm of 0.084 c;
4. Total column water vapor equivalent of 1.42 cm;
5. Total column ozone equivalent of 0.34 cm;
6. Surface spectral albedo (reflectivity) of Light Soil as documented in the Jet Propulsion Laboratory ASTER Spectral Reflectance Database.

Actually, we are speaking of an air mass coefficient: a relative measure of the optical path length passing through the Earth's atmosphere, as described for a fixed moment in time and space. We express the air mass coefficient as a ratio of the direct path of the global shortwave irradiance incident upon a specially tilted surface, relative to the path length for a horizontal surface (optical path oriented vertically upwards as the normal).

AM0

The first thing we need to estimate is what the intensity of the global horizontal irradiance would be just "outside" of our thin covering atmosphere. So, how do we determine the solar energy incident upon the extraterrestrial surface for the Earth-Atmosphere system?

First, we begin with the annual average solar constant, in units of irradiance (recently updated as of 2012! No longer 1366 or 1367 W/m² if you knew that value). The average annual Solar intensity will actually vary according to an oscillation linked to 11-year cycles of sunspots. Given a large number of sunspots, the solar constant will be higher (~ 1362 W/m²) while the value will drop to ~ 1360 W/m² when there are not many sunspots (changes about 0.01%). You can see NASA's Solar Radiation Climate Research Area (accessed Feb 13, 2013).
$$G_{sc}=1361W/m^2$$

Here, G is for Global irradiance, and "sc" stands for solar constant.

Second, we estimate the irradiance of the Sun for the intensity collected on a plane perpendicular to the beam shooting out from the Sun that is also perpendicular to the surface of the Sun (the normal radiant exitance). We would term that "normal global irradiance at AM0" (G_0,n). This would be the equivalent of an estimate at zero cosine projection error, or the angle of incidence is zero. The cosine function in the following Equation delivers the change from zero to one, reflecting the cyclic orbit of the Earth relative to the Sun. The parameter n in this equation is the day number in the year.
$$G_{0,n}=G_{sc}\left[1+0.033\cos \left(\frac{360n}{365}\right)\right]$$

Here, G is for Global, subscript "0" is for Air Mass Zero, and subscript "n" stands for radiant exitance normal to the surface of the Sun (don't confuse it with the day number).

Third and finally, we need to estimate the AM0 irradiance for any given horizontal surface on Earth's surface (G₀). Think about it, a horizontal surface on Earth (or just outside the atmosphere) will be tangent to the curvature of that locale on Earth. We should notice in the following equation that the Earth-Sun relations of declination ($\delta$ ), latitude ($\alpha$), and hour angle ($\omega$) are all included in this irradiance equation for AMO.
$$G_0=G_{sc}\left[1+0.033\cos \left(\frac{360n}{365}\right)\right]\cdot \left[\sin \varphi \sin \delta +\cos \varphi \cos \delta \cos \omega \right]$$

By comparison with our work from Lesson 2, I can point out that the equation is actually multiplying the Equation for G_0,n with the Equation for the solar altitude angle: ${\alpha }_s$ Another way to write this would be $G_0=G_{sc}\cdot \sin {\alpha }_s$ Wow! Lesson 2 really comes in handy!

As a reminder, the relation to find ${\alpha }_s$ is:
$$\sin {\alpha }_s=\left[\sin \varphi \sin \delta +\cos \varphi \cos \delta \cos \omega \right]$$

Consider that the sine of the altitude angle ($\sin {\alpha }_s$ ) is the same as the cosine of the zenith angle ($cos{\theta }_z=sin{\alpha }_s$ ).

• Hourly Irradiation for AM0:

$$I_0=\frac{12\cdot 3600}{\pi }\cdot G_{0,n}\cdot \left[\frac{\pi }{180}({\omega }_2-{\omega }_1)\sin \varphi \sin \delta +\cos \varphi \cos \delta \left(\sin {\omega }_2-\sin {\omega }_1\right)\right]$$

• Daily irradiation for AM0:

$$H_0=\frac{12\cdot 3600}{\pi }\cdot G_{0,n}\cdot 2\left[\frac{\pi }{180}({\omega }_{ss})\sin \varphi \sin \delta +\cos \varphi \cos \delta (\sin {\omega }_{ss})\right]$$

where the hour angle for sunset has been defined in Lesson 2 as:
$${\omega }_{ss}={\cos }^{-1}(-\tan \varphi \tan \delta )$$

AM1.5

The "standard" for testing. The air mass coefficient is defined in proportion to the cosine of the zenith angle (${\theta }_z$): the angle between the beam from the Sun and the normal vector pointing directly up to the zenith of the sky (normal to the horizontal surface).

$$AM=\frac{1}{\cos ({\theta }_z)}\text{[simple, parallel plate]}$$

One needs

• the day number (N),
• the declination ($\delta$),
• the hour angle ($\omega$), and
• the local latitude ($\varphi$) to calculate the zenith angle.

By equivalence, the cosine of the zenith angle is the sine of the altitude angle ${\alpha }_s$ , as we just demonstrated above.

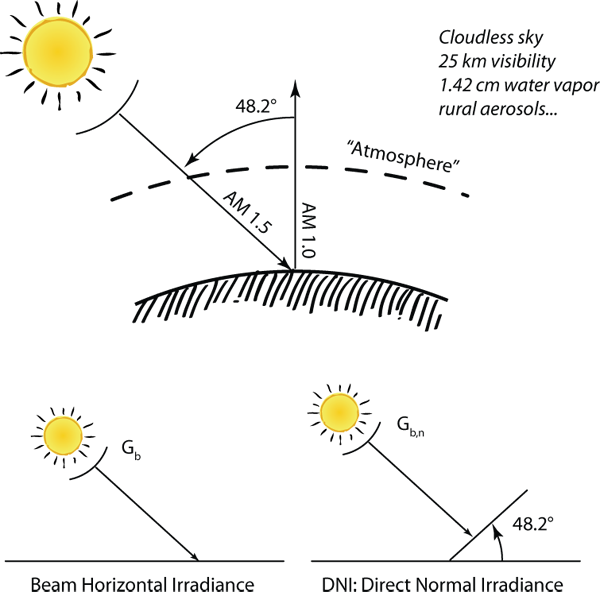
Figure 3.9 illustrates the concept of airmass with respect to a zenith angle of $\mathrm{\theta }={\mathrm{48.2º}}^{}$(AM1.5), or an altitude angle of ${\alpha }_s={\mathrm{41.7º. }}^{}$The hypothetical receiving surface would be tilted at ß = 37º for global irradiance G_t and an angle of incidence of  $$ θ = 11.2º. 

Gueymard has since developed a modified air mass model that will also apply for zenith angles >80°, as the former model tends toward infinity at ${\theta }_z=90°$ .

$$AM=\frac{1}{\cos ({\theta }_z)+0.00176759\cdot {\theta }_z\cdot {(94.37515-{\theta }_z)}^{-1.21563}}$$

Source: Matthew J. Reno, Clifford W. Hansen, and Joshua S. Stein. Global horizontal irradiance clear sky models: Implementation and analysis. Technical Report SAND2012-2389, Sandia National Laboratories, Albuquerque, New Mexico 87185 and Livermore, California 94550, March 2012.

---