2.9 Sun-Earth Relations
Reading Assignment
- SECS, Chapter 6: Earth-Sun Angles section
The following sections are closely coupled to the reading assignment, but I have enlarged the images for you. Our Solar Energy Conversion Systems are going to be fixed at some location on the surface of Earth, right? So, we will place an "Observer" at the future location and describe the relative position of the Sun and Earth and SECS. However, there are a few underlying spherical relations that do not depend on the location of the SECS or the observer.
This section discusses those geometric relations that are effectively "Independent of the Observer." Keep an eye out for the declination (delta, ), the latitude and longitude ( and ), and , the hour angle.
The Greek notation used below is now fairly standard for the field, but you may see different approaches in informal settings or unusual textbooks. I follow the established nomenclature defined by Beckman, et al., in the research journal Solar Energy in 1978, reprinted in Solar Energy in 1997. As noted earlier, the document is available to you from the Library E-Reserves.
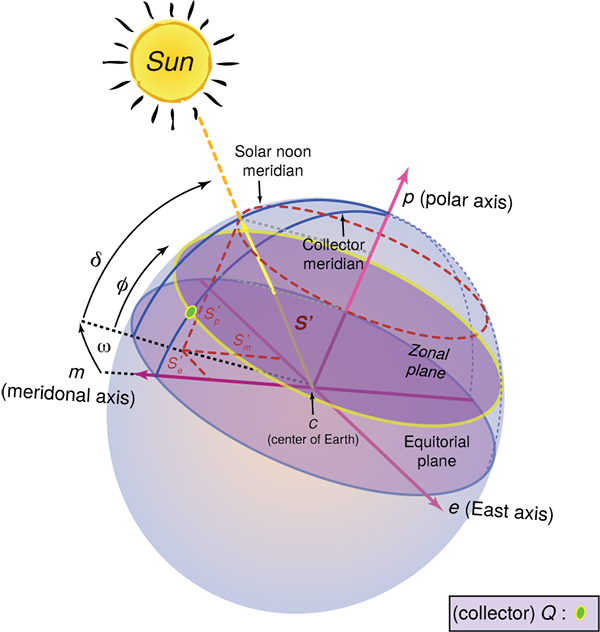
Hour Angle ():
Again, this is the way we represent the apparent displacement of the sun away from solar noon. An hour angle of zero degrees indicates that the sun is directly above, and the sign of the hour angle is determined by occurring either before noon (negative) or after noon (positive). Another way of looking at it is the difference in angle between the local meridian of the observer/collector and the meridian that the beam of the sun is intersecting at a given moment.
Angle of Declination ()
This is not an observed angle relative to the surface of the Earth and the Collector. Declination is the observed angle (due to the polar tilt) between the plane of the Earth’s equator and the plane of the ecliptic (the plane in which the Earth's orbit about the Sun lies). Declination has a maximum angle of 23.45° at either solstice. In this case of coordinates, the sun observed in the North is positive, and in the South is negative. One can imagine this as a series of sun paths over the course of a year. In contrast, the declination reaches a midpoint at either of the equinoxes. The range of declination is limited to Earth’s tilt: −23.45° (winter solstice) (summer solstice).
Declination is independent of location on the planet!
The declination can be calculated by a simple approximation (first equation) or a Fourier series (second equation).
where:
Angle of Latitude () and Longitude ()
The complement of longitude () in geospatial coordinates is the latitude. When combined together, we have identified a singular point on the surface of Earth. However, separately, they refer to arcs or circles spanning huge distances. We can look up the latitude and longitude of a site on a search engine like Google.
Key latitude angles of interest are:
- Arctic Circle = +66.56° North of this, the sun is above/below the horizon for 24 continuous hours at least once per year (during the solstices).
- Tropic of Cancer = +23.45° The maximum tilt of the North Pole to the Sun.
- Equator = 0°
- Tropic of Capricorn = −23.45° The maximum tilt of the South Pole to the Sun.
- Antarctic Circle = −66.56° South of this, the sun is above/below the horizon for 24 continuous hours at least once per year (during the solstices).