Lesson 8 - Methods of Prediction
8.0 Overview
Overview
We encounter two really big factors that create a spread of possible outcomes for energy systems when we look into the future: weather, and people demanding energy. In Lesson 8, we will advance our knowledge regarding the role of weather and the electric power grid. We will cover a general idea of risk and uncertainty. Then, we will show again that time and space are related using Taylor's Hypothesis. More important, we will describe how events in the future can be predicted (to certain degrees of confidence) from historical knowledge and from knowledge of present events that are connected spatially to the locale of interest. In particular, we are interested in tools used by meteorologists.
Both weather systems and demand on the grid (called loads) will be presented as dynamic, coupled parameters. Both weather and grid loads will deeply affect our clients in terms of the required decisions for solar technology deployment and management. Both will be shown to have a spread of possible outcomes for a given time horizon; and thus, there will be uncertainty and risk in making decisions.
Now, the point of Lesson 8 is to familiarize yourself with modern elements of time horizons that affect project risk assessment and management due to the dynamic behaviors of the grid and of the local weather systems. We are not going to give you the full chops of a meteorologist, no more than in the last lesson were we going to turn you into a financial analyst. The whole point of transdisciplinary research and practice is for experts from different disciplines to work jointly as a team around a shared goal (e.g., the goal of solar design) to address a common challenge. However, it is hard to work jointly on a team when you don't know the language of your team members. So, onward!
8.1 Learning Outcomes
By the end of this lesson, you should be able to:
- describe the role of risk and uncertainty in delivering solar resource units to the grid;
- describe the time-space relationship in meteorological assessment;
- list the current limitations of solar resource forecasting in time and space scales;
- list the relevant meteorological metrics for common SECS technologies.
What is due for Lesson 8?
This lesson will take us one week to complete. Please refer to the Course Syllabus for specific time frames and due dates. Specific directions for the assignment below can be found within this lesson.
| Required Reading: |
J.R. Brownson, Solar Energy Conversion Systems (SECS), Chapters 5, 8, and 9 (sections related to Risk, Time-Space, and Meteorology) W. Short et al. (1995) Manual for the Economic Evaluation of Energy Efficiency and Renewable Energy Technologies [1]. NREL Technical Report TP-462-5173. (read pp. 27-34: Uncertainty and Risk) |
|---|---|
| Optional Reading (not required): | J. Rayl, G. S. Young, and J. R. S. Brownson. Irradiance co-spectrum analysis: Tools for decision support and technological planning. Solar Energy, 2013. doi: http://dx.doi.org/10.1016/j.solener.2013.02.029 [5]. A. C. McMahan, C. N. Grover, and F. E. Vignola. "Evaluation of Resource Risk in Solar-Project Financing", Kleissl, J. ed. Ch 4 in: Solar Energy Forecasting and Resource Assessment (2013) Academic Press. F. E. Vignola, A. C. McMahan, and C. N. Grover. "Bankable Solar-Radiation Datasets", Kleissl, J. ed. Ch 5 in: Solar Energy Forecasting and Resource Assessment (2013) Academic Press. |
| To Do: |
Yellowdig Discussion: Space and time relationships in solar forecasting Engage in all Try-This and Self-check activities (not graded). |
| Topic(s): | Time Horizons Nowcasting Load Forecasting Numerical Weather Prediction (NWP) Weather Research & Forecasting (WRF) |
Questions?
If you have any questions, please post them to the Lesson 8 General Questions and Comments Discussion Forum. I will check the forum regularly to respond. While you are in a discussion, feel free to post your own responses if you, too, are able to help out a classmate.
8.2 Transdisciplinary What?
You don't have to know everything...
...but you'd better have a transdisciplinary team to really be competitive in the solar market. In this lesson and the next three, we are going to explore content for which you are not necessarily expected to be the expert. But you do need to know about the important roles of your future partners in design, and the core communication topics relevant to engaging them in the integrative design process.
On your dream team for solar design, do you have a meteorologist, an economist skilled in energy business and finance, a systems engineer, a quantitative analyst [6] to assess large data, a communications expert, and a practical electrician/roofer/plumber? Yes? Well, then you're way ahead of most everyone else. OK, does your team share a common framework: such as the goal of solar design? Do they understand and work to synthesize concepts across disciplines? Do they work together to address your problems?
This is just a quick review of the term "transdisciplinary." In exploring a spectrum of techniques for the last three content lessons, we are going further and further from "core" disciplinary topics. You know, we've been saying that this integrative design process is pretty important, and it involves a transdisciplinary approach. But what does that mean, and how is it practical to the core philosophy of a solar design team?
Levels of Integrative Design Teams
- (Level Three) Transdisciplinary: contributors are from different disciplines, working jointly to explore and apply a shared conceptual framework that synthesizes discipline-specific theories, concepts, and approaches. Transdisciplinary work extends methods and concepts to address common problems, often in transformative new ways.
- (Level Two) Interdisciplinary: contributors work jointly, but still carry discipline-specific perspectives while working to address a common problem. Results tend to be reported as partial contributions in a discipline-by-discipline sequence, and each contribution of knowledge is partitioned from other relevant elements.
- (Level One) Multidisciplinary: contributors are from different disciplines, working sequentially from their own discipline-specific perspectives. The goal is to combine results at the end of the project to address a common problem.
- (Silos) Single Discipline: contributors work together within a single discipline to address a problem.
Reference:
Patricia L. Rosenfield (1992) The potential of transdisciplinary research for sustaining and extending linkages between the health and social sciences, Social Science & Medicine, 35(11) 1343-1357. DOI: http://dx.doi.org/10.1016/0277-9536(92)90038-R [7]
If we really want to see solar energy grow in new directions and adapt quickly to the diversity of challenges in society and the environment, then we need to get comfortable with "not knowing" everything, or even not knowing a lot. The patterns are generally just too big for a single person to be able to hold all of the core knowledge and be able to execute the design-build-operate process alone. We also need to get comfortable with building knowledge across disciplines, linked by a common conceptual framework. We need integrative design teams that "get" the value of transdisciplinary work.
8.3 Uncertainty and Risk
Reading Assignment
- J.R. Brownson, Solar Energy Conversion Systems (SECS), Chapter 9 (section on Utility, Risk, and Return)
- W. Short et al. (1995) Manual for the Economic Evaluation of Energy Efficiency and Renewable Energy Technologies [1]. NREL Technical Report TP-462-5173. (Read pp. 27-34: Uncertainty and Risk.)
What is Risk?
In solar project design and project management, we would like to work for our clients to minimize risk. We describe risk as the dispersion of outcomes around an expected value. Something is riskier if the spread of possible outcomes is bigger around an expected value. The more specific terms of variance and standard deviation describe the spread of data (the dispersion) about an expected value. Events that occur in the future will have a spread of possible outcomes, because we cannot know the final value for the future with 100% confidence until it actually occurs.
When we really know what to expect, what we imply is that the dispersion of possible outcomes is clustered tightly about that expectation. From that information, we can adapt or make changes for the future appropriately. However, knowing the spread of possible outcomes about an expected value is deeply important, even if you know that the spread of outcomes is very broad. The greater the dispersion of outcomes, the higher the risk. In our reading, we comment that “riskier” scenarios in solar project development, or systems operation and management, will have a larger dispersion of outcomes around the expected value.
Risk is often framed as the probability of an uncertain event occurring in the future multiplied by the expected loss should the event occur. We call the model of the probability distribution the pdf, or the probability distribution function. Note that there are specific applications for continuous or discrete distributions (cf. probability density function [8], and probability mass function [9]). If we know the probability distribution [10] of all possible outcomes, then we also know the expected value of the outcome, surrounded by the dispersion of outcomes around that expected value. If the pdf is normalized, then the probability of any event can be evaluated by integrating a section under the curve. If we integrate under the entirety of a normalized pdf, then we are integrating across all possible outcomes. The total probability is then equal to 1.
Variance in Data
A common measure for the spread of data can be the variance [11] ( ). Given a sample of multiple events, the variance is a measure of the spread of the data about an expected value or outcome. We have also discovered in our reading that a portfolio of renewable energy can potentially be used to reduce the variance of the power generation coupled to the same grid. This is something to bear in mind in the future of large, distributed PV.
In Figure 8.1, below, we present a normal probability distribution function (also called a Gaussian). Now, many distributions in solar energy are not normally distributed, but this is a starting point. The data tends to be strongly skewed toward clear days (more clear days than overcast), or bimodal in nature. Quantitative analytics often use available statistical software such as R (The R Project for Statistical Computing) [12] to estimate density functions based on discrete real data (e.g. a histogram). This is called density estimation [13]. The peak(s) in a pdf represent the highest likelihood of expected values.

Self-Check
8.4 Exceedance Probabilities: P50, P75, P90
Reading Assignment
- A. Dobos, P. Gilman, M. Kasberg (2012) "P50/P90 Analysis for Solar Energy Systems Using the System Advisor Model." [2] Presented at the 2012 World Renewable Energy Forum Denver, Colorado May 13-17, 2012.
- Rhino Energy web page: "Exceedance Probabilities [3]." Accessed Oct. 20, 2013.
Using Exceedance Probabilities
Because the solar resource is intermittent (variable), so too is the power production from a technology such as PV. The expected values and the spread for natural data like the weather is not necessarily "normally distributed" or even unimodal (one peak). This is why we often plot histograms of the data to observe the manner in which the data is spread out.
We would like to describe our level of confidence that a certain level of power production (or capacity) will be met, in order to minimize the risk in managing a system. In our "Try This" example, we saw how a data set can be summarized using quartiles (minimum, 25%, 50% or mean, 75%, and maximum). So, in this case, we would like to break the spread of data into bins that are both useful and tied to probabilities.
A value of "P50" or "P90" (or any value from 0-100) describes an annual value of power production from the intermittent resource with a probability of 50% or 90%, respectively. In fact, that quartile summary can be viewed as P25, P50, and P75. For P50, there is a 50% chance that the mean power production will not be reached at any given time. For P90, there is a 10% chance that the P90 level will not be reached.
Banks and investment firms working on wind farm projects often require P50 and P90 values of the wind resource at a location to determine the risk associated with a project’s ability to service its debt obligations and other operating costs.
-Dobos, Gilmanjavascript:submit_mid('sp_ig_all'), Kasberg (2012)
Inside of the SAM software, there is an advanced feature to evaluate P50/P90. There is an accessible database (*.cbwfdb file format, a proprietary format developed for SAM's P50/P90 capability) from the National Climatic Data Center [16] (NCDC). The database is quite large (1.1 GB) but allows us to explore a number of cases for this course.
The long term NCDC/NSRDB dataset includes the impact of large volcanic activity and other phenomena that occur on timescales larger than one year. In particular relevance to solar plants, the eruption of Mt. Pinatubo introduced large quantities of aerosols into the atmosphere that reduced incident irradiance levels between 1991 and 1993. Other variations include the cyclic El Niño and La Niña phenomena, as well as the 11 and 22 year sun spot cycles.
-Dobos, Gilman, Kasberg (2012)
8.5 Coordination Challenges in Time and Space
Reading Assignment
- Alexandra von Meier (2011) "Integration of Renewable Generation in California: Coordination Challenges in Time and Space [17]" (white paper for California Institute for Energy and Environment (CIEE))
- [Review] SECS, Chapter 5 - Meteorology: the Many Facets of the Sky (sections:"Spatio-Temporal Uncertainty" and "Robot Monkey does Space-Time")
- [Review] SECS, Chapter 8 - Measure and Estimation of the Sun (sections: "Pyranometer: Global Irradiance Measurements," "Diffuse and Direct Normal Measures", and "Satellite Measures of Irradiation")
- Optional: J. Rayl, G. S. Young, and J. R. S. Brownson. Irradiance co-spectrum analysis: Tools for decision support and technological planning. Solar Energy, 2013. doi: http://dx.doi.org/10.1016/j.solener.2013.02.029 [5].
The Grid: it's complicated
Ok, so after digging into Dr. von Meier's paper on the grid, we should have noticed a few things. First, renewables in CA are continuing to grow as a contributing portion of electricity generation. Second, the power grid linked with CA (the Western Interconnection) will have to accommodate the new sources of power just as the grid has to accommodate new loads (sources of demand). Before renewables, we had baseload power mainly from coal, nuclear, and hydroelectric, and everything was pretty smooth on the generation side of the equation. But now, wind and solar power are pushing in with "intermittent power."
In essence, renewable and distributed resources introduce spatial and temporal constraints on resource availability: we cannot always have the resources where we want them, when we want them.
-A. von Meier (2011)
This is a really neat paper, in that it points out the orders of magnitude of challenges that the markets and grid operators have to deal with on a regular basis, both spatially and temporally! And yes, you might also note that those scales were incorporated into Figure 5.10 of the SECS textbook for the Fujita relation of meteorological phenomena in space and time. You can compare the units in the von Meier paper with the table and graphic below.
We just learned that large portions of the electricity grid can be managed by an Independent System Operator (ISO, or RTO), where demand on the grid is managed through markets. That is great, but the grid also has problems that accumulate anyway, which need to be dynamically adapted to by the utilities or the clients. In our main reading, we see all the different systems elements that need to be coordinated in our power grids. These are amazingly complicated systems that are then perturbed by pesky things like weather.
Coordination in Time:
- Power Systems Management and Markets: Regulatory and technological parameters occur over time spans from years to days, to less than 1 minute (>6 orders of temporal magnitude). Pay special attention to Day Ahead Scheduling and Hour Ahead Scheduling while reading about markets.
| Temporal Phenomenon | Short | Long | Unit |
|---|---|---|---|
| demand response | 4 | 4600 | sec |
| hour-ahead scheduling | 1.75 | 7 | hour |
| service restoration | 0.5 | 28 | hour |
| day-ahead scheduling | 18.5 | 48 | hour |
| T&D Planning | 1 | 16 | year |
| Carbon emissions goals | 13 | 80 | year |
Coordination in Space:
- Regional Power Grid Behaviors: Power responses, natural stability problems within the grid, transmission congestion, and regulatory scopes can happen over distances from thousands of kilometers down to tens of meters (>5 orders of spatial magnitude).
| Spatial Phenomenon | Short | Long | Unit |
|---|---|---|---|
| DG interconnection criteria | 50 | 20,000 | m |
| voltage regulation | 0.5 | 10 | km |
| distribution feeder | 2 | 25 | km |
| transmission congestion | 25 | 1,000 | km |
| stability problems | 500 | 3,000 | km |
| CAISO | 450 | 800 | km |
| WECC | 1,600 | 3,000 | km |
The Weather: yep, complicated too...
The weather systems that we deal with have their own orders of magnitude in time and space. Let's compare the time and space for weather phenomena in the following graphic. We saw this image in Lesson 3; but now, we can see that those time and space scales above actually fit with the scales right here, described by Ted Fujita. Notice the line that trends through the data of clouds (which are the nemeses of solar energy...). From a fit of $17\ m/s$, we have a quick conversion tool to flip between characteristic time scales and characteristic distance scales! Just remember $17\ m/s$ as the FRYB relation (Fujita-Rayl-Young-Brownson), and how to convert time from hours to seconds (3600 seconds in an hour), or kilometers to meters (you don't need that conversion, do you?).
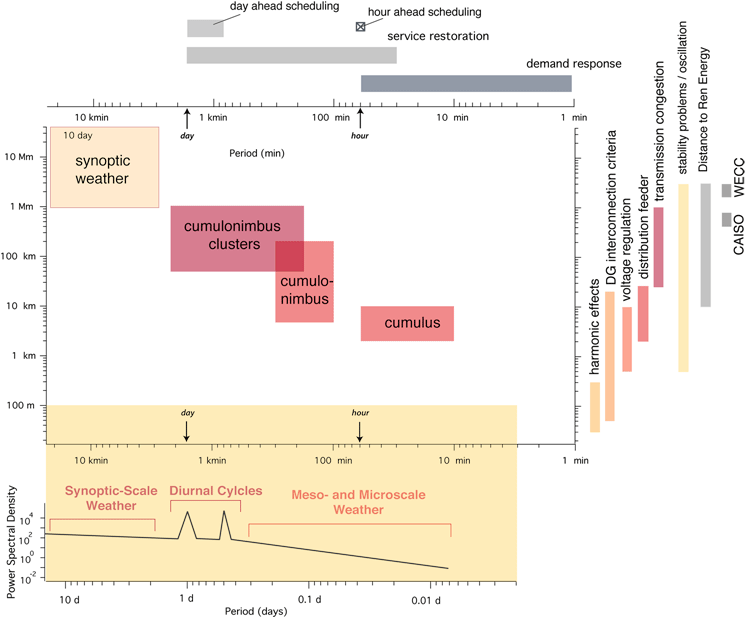
8.6 Putting it together: Supergraphic
Overlaying the Grid with the Weather
Now that we know a few things about the scales of time and space for the power grid (using CAISO and WECC for scale), we can compare it with the weather scales. Look to the top and right for the von Meier scales, and the core diagram in the center for the Fujita scales. The diagram on the lower portion shows us a rough sketch of the power spectral density for the meteorological spans of synoptic, mesoscale, and microscale weather.
By applying the average meteorological advection speed of , (which we are calling the FRYB relation for the class), we can convert an example spatial scales of variability associated with transmission congestion (red vertical bar on the right) from distances of 25-1000 km into a time horizon. The relevant time scales for meteorological phenomena exist within 25 minutes to 16 hours (involving events from cumulus, cumulonimbus, and cumulonimbus clusters interfering with the Sun's irradiation).
Alternately, we observe that the harmonic effects propagating within the grid along distances of 30-300 meters would be relevant for meteorological phenomena spanning 1.8-18 seconds. This scale of events is too small to be incorporated into the presented meteorological phenomena.
 [19]
[19]
8.7 Discussion Activity
Relations in Time and Space
You have been reading about the relations between time and space, and you have read about different time horizons of interest to the solar energy and electric grid fields. Now, let us apply that knowledge to Table 8.2 from the Chapter by Coimbra, Kleissl, and Marquez (2013).
| Technique | Sampling Rate | Spatial Resolution | Spatial Extent | Suitable Forecast Horizon | Application |
|---|---|---|---|---|---|
| Persistence | High | 1 point | 1 point | Minutes | Baseline |
| Sky-Imagery | 30 sec | 10-100 m | 2-5 m radius | Tens of minutes | Short-term ramps, regulation |
| GOES Satellite Data | 15 min | 1000 m | U.S.A. | 5 hours | Load following |
| NAM weather model | 3600 sec | 12 km | U.S.A. | 10 days | Unit commitment |
Questions to discuss:
- Based on the FRYB (Fujita-Rayl-Young-Brownson) relation of 17 m/s and the given "Sampling Rate" for each method (in Table 8.3), what is the characteristic meteorological distance scale being sampled (easy conversion)? How do those distances compare to the "Spatial Resolution" scales provided in the table?
- Now take a moment to read up on the Nyquist-Shannon Sampling Theorem [20], where you will focus on the Nyquist rate. Do all of the systems listed in the table meet the Nyquist sampling rate, and if so, for what minimum resolution?
Please share your reflections on these questions in the Yellowdig community. I wonder if everyone will come to the same conclusions.
Tagging
When you create a post in the Yellowdig discussion space, you are required to choose a topic tag. For Lesson 8 discussion, please use these tags:

Grading
Yellowdig points you earn over the weekly point earning period (from Saturday to next Friday) will count towards 1000 pts. weekly target. But you can go above it (to 1350 pts. max). Yellowdig discussions will account for 15% of the total grade in the course.
Deadline
There is no hard deadline for participating in these discussions, but beware of the weekly limit. You need to create posts every week to stay on target with your total discussion participation grade. Each weekly point earning cycle ends Friday night, and a new period starts on Saturday.
8.8 Time Horizons of Interest
Reading Review
- J. Kleissl (ed), 2013. Solar Energy Forecasting and Resource Assessment. Elsevier Science, Academic Press. Read pp. 171- 177 from Chapter 8: "Overview of Solar-Forecasting Methods and a Metric for Accuracy Evaluation", by Coimbra, Kleissl, and Marquez
Electricity Markets and Grid Management
The first forecasts that we will explore from the reading are related to the modern electrical power grid. You are about to observe us jump from a +20 year time horizon in Lesson 7 (Life Cycle Cost Analysis), right down to spans of days and hours. If you recall from the reading by von Meier, this jump in orders of magnitude is pretty common for analysis related to financial and engineering decisions in energy systems.
Within the technological ecosystem of the grid, one follows the demand for electricity. Recall from Lesson 7 that the term for energy demand (including losses) is called the Load. Supply must be managed to match those dynamic demands. So, why might we forecast for loads in the electricity market? The time horizons of interest to engineers and financial experts working with the grid have been developed within the technical ecosystem of the modern power grid. When managing the grid as a dynamic system, we can think in time spans of seconds to minutes (Intrahour), over a few hours (Intraday), and over the course of a few days (Intraweek).
CAISO Example
Recall that California mainly has an Independent System Operator, with the exception of entities like SMUD (Sacramento Municipal Utility District). Also recall that an ISO uses markets (a zonal or nodal market) to manage the grid. In the last super graphic, which tied together weather scales and grid management scales, we observed "Hour Ahead" and "Day Ahead" markets along the top. But in our reading, we see that the time horizon is a bit different from the simple description:
- Day Ahead Market: Operational Day begins at 12:00a in the morning.
- Release load forecast at 5:30a in the morning of the day prior to the operational day. This means a +18.5h lead time from the beginning of the forecast. (5h:30 + 18h and 30 min = 24h)
- The forecast ends at ~11:59p of the forecast day. The end of the forecast is a +42.5h lead time from the end of the forecast that was initiated at 5:30a the day before. (5h:30 + 42h and 30 min = 48h)
- Hour Ahead Market: Operational Hour begins at the 0h.
- Release the hourly load forecast 1h and 45 min prior to the operational hour.
- Also release an advisory forecast with a +7h window from the beginning of the operational hour.
- Other Planned Markets: CAISO is considering intrahour forecasts for 5 minute intervals. Midwest ISO already does this.
- FERC: Notice of Proposed Rulemaking -- opportunity to schedule transmission every 15 min.
Time Horizons of Interest to Meteorologists
By reviewing the reading on Taylor's Hypothesis in Ch. 5 of the SECS text, we see that periods in time and distances can be related: a series of changes in time for a fixed place is due to the passage of an unchanging spatial pattern over that locale. So, in the following list, we can connect space and time (in fact, we do the same for power systems).
Taylor’s hypothesis permits a time series of irradiance observations over fixed locations to be converted into an equivalent translation across space (at the advective or propagation speed to the corresponding spatial pattern). Hence, all time scales are also spatial scales so long as the advective wind speed is much greater than the time scale of the evolving meteorological event being investigated, as is often the case.
-Brownson, SECS (2013)
Just keep this in mind with forecasting, as units of time actually also imply units of distance, and vice versa.
- Synoptic-scale weather: large-scale meteorology (also termed cyclonic-scale), with common atmospheric phenomena spanning 1000–2500 km (or days to month)
- Mesoscale weather: common atmospheric conditions spanning hundreds of kilometers (minutes to hours)
- Microscale weather: common atmospheric conditions spanning approximately 1 km (minutes)
Self-Check
8.9 Forecasting Summary
Reading Review
- J. Kleissl (ed), 2013. Solar Energy Forecasting and Resource Assessment. Elsevier Science, Academic Press.
The reading continues for pp. 177-182 of Chapter 8: "Overview of Solar-Forecasting Methods and a Metric for Accuracy Evaluation," by Coimbra, Kleissl, and Marquez [found on Canvas] - Optional: The sections following 8.2 (pp. 182-192) can be scanned for key topics rather than a deep read. 8.3 deals with metrics for evaluating models, which is a deeper statistical investigation than we have time for here. Also, those methods are still evolving in collaboration with meteorologists.
Forecasting
Reading Summary
A quick reminder, summarizing the reading from the previous page.
- >6 hour time horizon: physics-based models
- 2-6 hour time horizon: combination of methods via Numerical Weather Prediction (NWP) models
- <30 minute time horizon: apply ground-to-sky imager technologies
Events to be evaluated for <2 hours will use statistical approaches such as time series (Autoregressive Integrated Moving Average; ARIMA) or artificial intelligence (e.g., Artificial Neural Networks; ANN).
Meteorology-Specific Forecasts
As a slight correction from the reading assignment, we provide the following standard terminologies in meteorology for forecasting ranges, called lead times. These are not stated clearly in the reading, and they are important enough to have in your vocabulary. In the prior reading assignment, you should notice that the time horizons tied into solar energy models are not yet aligned with the approaches for meteorological forecasting. This is an indication of the relatively new start of forecasting applied to solar energy. We are still learning the common language of meteorology, and hopefully that language will soon converge. Similarly, meteorologists are beginning to adapt to the solar field's language of GHI, DNI, irradiation, etc.
- Medium-range: 3-7 days
- Short-range: 6 hours to 2 days
- Nowcast: 0 - 6 hours
- Hindcast: negative lead time
Numerical Weather Prediction (NWP)
Numerical Weather Prediction [21] uses an assemblage of modeling methods, along with current weather observation data to forecast weather in a future state. Note that the observations tied to the current state of the data are very important to NWP.
- Rapid Refresh from NOAA. [22]
- North American Mesoscale Forecast [23] (NAM) (mentioned in Table 8.1 of the reading).
Weather Research and Forecasting (WRF)
Local dedicated NWP models have been developed as a collaboration among NOAA and NCAR. The approach is termed WRF (pronounced "worf") [24]. This is an advanced application of NWP, but the skill with which one can forecast will still decay with increasing lead times due to the chaotic atmospheric behavior.
The Weather Research and Forecasting (WRF) Model is a next-generation mesoscale numerical weather prediction system designed to serve both atmospheric research and operational forecasting needs. It features two dynamical cores, a data assimilation system, and a software architecture allowing for parallel computation and system extensibility. The model serves a wide range of meteorological applications across scales ranging from meters to thousands of kilometers.
-WRF Homepage [24] (Accessed Oct. 20, 2013)
Research Occurring Now!
- Perez Research Group [25] at SUNY-Albany
- UCSD Solar Resource Assessment and Forecasting Laboratory [26] (Kleissl) and Coimbra Energy Group [27] (Coimbra)
8.10 Summary and Final Tasks
Summary
As a recap, in Lesson 8 we established that transdisciplinary research is a core part of integrative design, and while each of us doesn't need to be an expert in every field, we do need to stretch ourselves to understand and integrate our approach towards a common framework. In solar energy, that framework is tied to the goal of solar energy design and the foundations of sustainability systems. We then explored the role of risk and uncertainty in delivering solar resource units to the grid or managing the energy outputs on site, and defined risk as the dispersion of outcomes around an expected value, using the statistical variance of the data as a metric. Another way to explore dispersion from a banking and finance perspective has also been developed for renewables, using exceedance probabilities.
We then described the time-space relationship in both the grid, markets, and meteorological assessment. While there is still a lot to learn about the complex systems of weather, energy markets, and people demanding energy from the grid, we at least established a map to explore the scales of relevant time and distances using a general Earthly atmospheric advection speed of , which we dubbed the FRYB relation.
We explored the early methods to forecast solar energy metrics, and we found that some of the current limitations of solar resource forecasting are tied to the early nature of the field, while others are based in the general diminishing skill to forecast further into the future due to the chaotic nature of the Earth's atmosphere. We discovered that resolution limitations can be found in either spatial or temporal scales, too.
The relevant meteorological metrics for many common SECS technologies are tied into DNI, but we see that the field currently has very few methods to evaluate DNI to a high accuracy without directly measuring the parameter with expensive equipment. Finally, we note that most solar forecasts are linked to GHI only, which has limited value given our prior knowledge of the inherent error bound to Liu and Jordan-style transformations of GHI to and , and later POA for oriented arrays. These transformations also hold very little value to extract a meaningful DNI measure. This should be a reminder that the field of solar forecasting is still young, and we should be on the lookout for new progress that will enable us to minimize risk for our clients, hopefully increasing their solar utility in the respective locale!
Reminder - Complete all of the Lesson 8 tasks!
You have reached the end of Lesson 8! Double-check the to-do list on the Lesson 8 Learning Outcomes page to make sure you have completed all of the activities listed there before you begin Lesson 9.