3.2. Apparent daily path of the sun
For most solar tracking applications, we need a reasonably accurate knowledge of where the sun will be at a specific hour during each day in a year. Theory is well-developed to calculate the sun position with respect to the observation point on the earth surface, and it sets the background for design and modeling of both photovoltaic and concentrating solar power systems of various scale.
In order to discuss tracking or any other adjustments of solar receivers, it would be useful first to understand the sun's path across the sky dome. We are going to turn to the following reading, which describes the key parameters of the solar motion.
Reading Assignment
Book chapter: Kalogirou, A, Solar Energy Engineering, Chapter 2: "Environmental Characteristics." pp. 51-63. (See E-Reserves via the Library Resources tab.)
This reading explains a lot about the geometry of sun movement, provides the key equations and example calculations alongside with them. The objective here would be to learn how to estimate the sun position and draw its track for a particular location and time of the year.
The above materials provide the main tools for predicting the position of the sun at a location of choice at any specific time. Let us summarize a few key takeaways from this reading.
Solar Altitude and Solar Azimuth
The main parameters to determine are solar altitude (α) and solar azimuth (z). Here are the equations that are used to calculate these coordinates:
|
(3.1) |
|
(3.2) |
Let us consider an example showing how to use these equations.
Example
Calculate the solar position for Abu-Dhabi (UAE) on January 15 at 2 pm local time.
For this calculation, we will use equations (3.1) and (3.2) to find the solar altitude and solar azimuth, respectively. We will need to find the following parameters:
L - local latitude - Abu-Dhabi coordinates are: latitude 24.492o N, and longitude 54.358o E
You can use this website to get GIS data.
δ - declination - It is a function of the day of the year (N). For Jan 15, δ = -21.27o
as found by Eq. (2.5), Kalogirou's text.
h - hour angle - It is a function of the time of the day. For 2 pm, h = 22.04o as found by Eq. (2.9), Kalogirou's text. For calculating hour angle, you need to determine the apparent solar time (AST), which is given by Eq. (2.3) of Kalogirou's text.
You can also use this helpful resource and embedded calculator to find AST. (You may want to bookmark it to use in your homework!)
Applying it to the current location, we find that AST = 13.47 hr decimal time or 1:28 pm clock time. And the hour angle will be:
h = (AST-12) x 15 = (13.47 - 12) x 15 = 22.04
Now we can plug these L, δ, and h numbers into Eq. (3.1):
sin(α) = sin (24.493o)sin(-21.27o) + cos(24.492o)cos(-21.27o)cos(22.04o) = 0.6356
α = 39.47o
For solar azimuth, we use Eq. (3.2):
sin(z) = cos(d)sin(h)/cos(α) = cos(-21.27o)sin(22.04o) / cos(39.47o) = 0.453
z = 26.93o
This calculation can be essentially used for any location and any time in a year. The algorithms available help to produce detailed solar resource data for different settings. These data are available for reference and use, so you do not have to calculate all things from scratch, although it is useful to understand the theoretical background of it.
Sun Path Chart Tool
We can use the Sun Path Chart Program calculator at the University of Oregon's Solar Radiation Monitoring Laboratory website to obtain a complete picture of sun movement throughout the year. The calculator allows data to be plotted in either orthogonal or polar coordinates. For example, the diagram below (Figure 3.2) was obtained for the same location (Abu Dhabi).
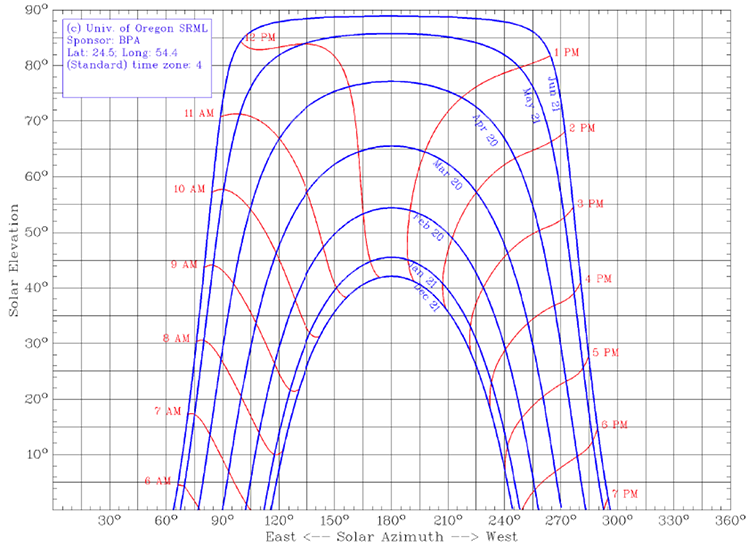
In this diagram, the solar altitude (elevation) is plotted versus solar azimuth, as shown by the blue curves for each date. There are a few representative dates shown, and January 21 is the closest to the calculation example previously given. Note that the solar azimuth is given on the 360o scale, with 180o corresponding to the south. Alternatively, Kalogirou uses the coordinate system and formulae to calculate solar parameters versus 0o as true south, with negative azimuth values corresponding to morning and positive azimuth values corresponding to afternoon hours. So beware of that difference if you try to match data from both sources. On the Sun Path diagram, the hourly position of the sun is marked by the red curves. In this particular case, the local standard times are plotted, while a similar diagram can be made in terms of solar time.
Check Your Understanding - Questions 1-3
Check Your Understanding - Question 4
Is it possible for the sun to reach 90° altitude at any time in a year in the following states? Type "yes" or "no" for each location. Can you explain why?
Arizona
Pennsylvania
California
Hawaii
Problem 3-1: Solar path calculation
(This calculation will be submitted as part of Lesson 3 problem set).
- Go to the Sun Path Chart Program calculator and calculate the sun path for a location of your choice. Use the orthogonal projection. Save your diagram.
You may need to find geographical coordinates and time zone for your location as input. Here is one of the websites that can be conveniently used for that purpose: TimeandDate.com. Just type in your location and get the data.
- Using equations (3.1) and (3.2) in this lesson, perform a manual calculation of the sun position (solar altitude and solar azimuth) for the same location on February 20th, at 12 pm and 3 pm local time.
- Mark your manual points on the diagram. Are you able to match your calculations with the plot?
The above materials and activity make sure that you can employ proper tools for defining solar position on the sky dome. Further on, the receiver positioning algorithms will use this information as the operational basis. Different types of tracking systems are discussed in the next section of the lesson.
