Gradient Solubility Model

Gradient Solubility Model

Because of the large disparity in structure and properties of asphaltenes and oil fractions in VDR, it is surprising that VDR appears as a solution (one-phase material) rather than a suspension of discrete asphaltene particles in VDR. A commonly accepted hypothesis to explain the single phase observed with VDR is known as the gradient solubility model, illustrated in Figure 5.6. The model claims that asphaltene molecules (depicted as dark spheres in Figure 5.6a) can be dissolved in resins (light spheres) and the resulting solution can be dissolved in oil (wiggly lines), thus producing a single phase solution. Some model molecular structures proposed for asphaltenes are shown in Figures 5.6b and 5.6c. There is a more widespread acceptance of the smaller molecular structures shown in 6c, as better representatives of asphaltenes molecules among the asphaltene researchers.

Figure 5.6a. Gradient-solubility model to explain dissolution of asphaltenes in crude oil.

Credit: Dr. Semih Eser © Penn State is licensed under CC BY-NC-SA 4.0

Figure 5.6b. Proposed molecular structures for asphaltene molecules.

Credit: Dr. Semih Eser © Penn State is licensed under CC BY-NC-SA 4.0

Figure 5.6c. Another proposed molecular structures for asphaltene molecules.

Credit: Dr. Semih Eser © Penn State is licensed under CC BY-NC-SA 4.0

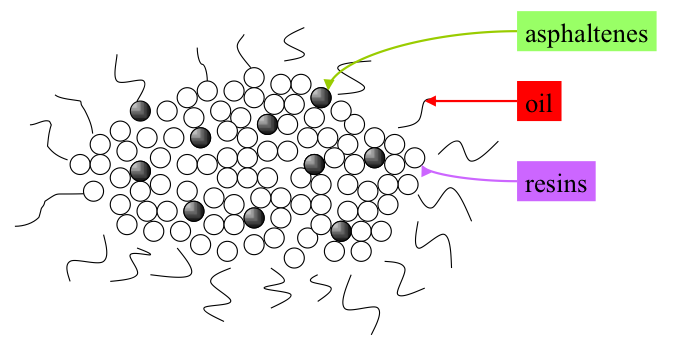
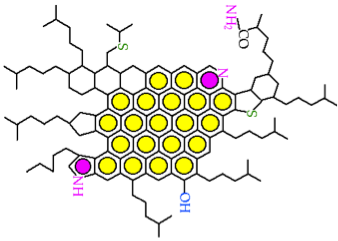
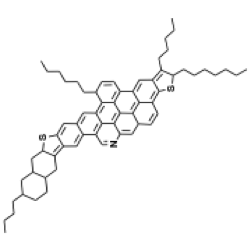
The gradient solubility model offers an explanation of how asphaltenes can be forced out of the solution in VDR by solvent extraction. Briefly, the solubility of a compound in a given solvent depends on the strength of the solvent that is measured by Hildebrand Solubility Parameters (HSP) for non-polar solvents. The two definitions of HSP are given in Figure 5.7, indicating the dependence of the parameter values on surface tension and molar volume of the solvent (1st Hildebrand parameter), or on the energy of vaporization (heat necessary to evaporate the solvent under constant volume conditions) and molar volume (2nd Hildebrand Parameter), respectively. These parameters correlate well with one another, and each can be used without any preference to express the dissolving power of a solvent. A discussion of the Solution Theory is beyond the scope of this course, but it would suffice to consider that solubility parameter increases with the increasing density (decreasing molar volume) and increasing surface tension, or increasing latent heat of vaporization. This explains why aromatic solvents have higher solvent power than aliphatic hydrocarbons, and why the solvent power of paraffins decreases with the decreasing carbon number.

It is now possible to explain that using a large volume of a paraffin solvent, added to dissolved VDR in a laboratory experiment, effectively disrupts the gradient solubility of asphaltenes, and as a result, asphaltenes precipitate as solid particles and can be filtered out for recovery. In refinery deasphalting process, however, e.g., in propane deasphalting [1], lower quantities of solvent (or lower solvent to resid (S/R) ratio) is used to separate asphalt (asphaltenes + resins) and deasphalted oil (DAO).

Figure 5.7. Hildebrand solubility parameters for non-polar solvents.

Click here for a text alternative to the figure above

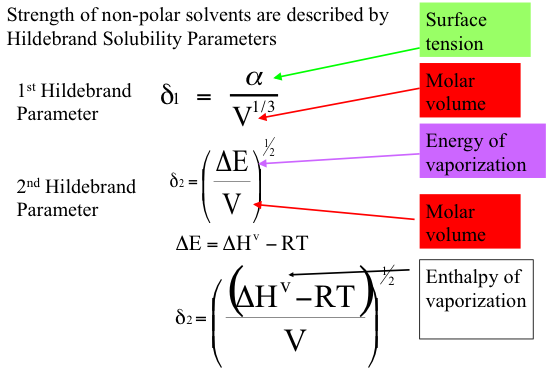
Strength of non-polar solvents are described by Hildebrand Solubility Parameters.

1^st Hildebrand Parameter:

$$\delta _ { 1 } = \frac { \alpha } { V ^ { 1 / 3 } }$$

2^nd Hildebrand Parameter:

$$\delta _ { 2 } = ( \frac { \Delta E } { V } ) ^ { 1 / 2 }$$

$$\Delta E = \Delta H ^ { v } – RT$$

$$\delta _ { 2 } = ( \frac { ( \Delta H ^ { v } - R T ) } { V } ) ^ { 1 / 2 }$$

Key: α = Surface Tension, V = Molar Volume; ΔE = Energy of Vaporization;ΔH=Enthalpy of Vaporization

$$$$  

Credit: Dr. Semih Eser © Penn State is licensed under CC BY-NC-SA 4.0