As we can see in the above graphic, there are quite a few materials terms that are used when describing the properties of materials. In this lesson, we are going to define the above terms. It turns out that many of the above terms are related to the stress-strain curve of a material. What are stress and strain, and how are they related?
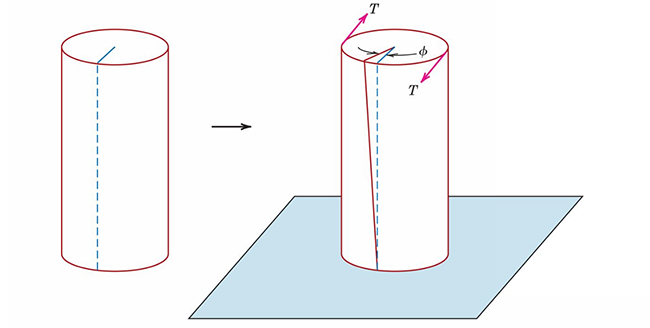
Let us take a cylinder and stress it. To stress it, I would fix one end of the cylinder and pull from the other end as shown in the figure below.
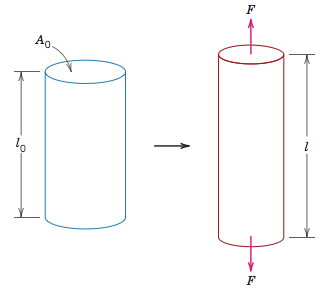
According to Newton's third law, the cylinder will experience a force downward on the lower surface of the cylinder and an equal and opposite force on the upper surface of the cylinder. My cylinder has an original length of Io and surface area of Ao. As I pull on my material with the force F the cylinder will lengthen and the resulting length will be l. Stress, σ, is defined as the force divided by the initial surface area, σ=F/Ao. This pulling stress is called tensile stress. Strain is what results from this stress. Strain, ε, is defined as the change in length divided by the original length, ε
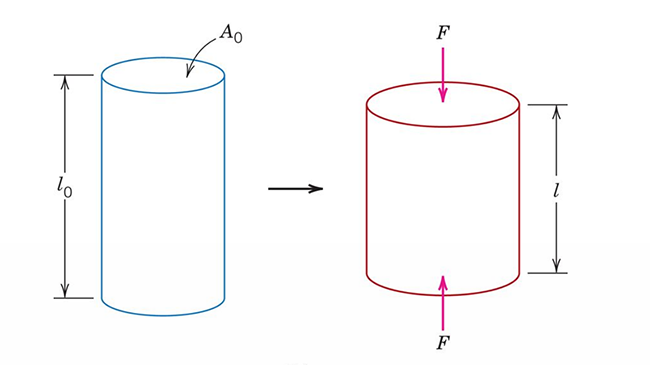
If instead of pulling on our material, we push or compress our cylinder we are introducing compressive stress. This is illustrated in the following figure:
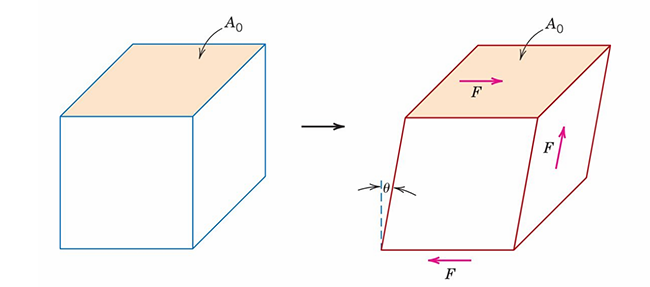
If instead of applying a force perpendicular to the surface, we apply parallel but opposite forces on the two surfaces we are applying a shear stress. This is illustrated in the following figure:
Stress related to shear is torsional stress. If we hold one end of our cylinder fixed and twist the other end as shown in the figure below, we are applying a torsional (or twisting) stress.