Overview

Meteorologists devote their lives to one purpose: to forecast the weather. But many other scientists work to build our understanding of the atmosphere, which is the basis for better prediction that meteorologists can use. Atmospheric science is the foundation upon which all meteorology is based.

Just as with all other physical sciences, mathematics is the language of atmospheric science. If you had our first-year meteorology course, you learned about weather forecasting and some of the physical basis behind the forecasts. This course will introduce you to even more physical concepts of atmospheric science and some of the mathematics that describe and quantify those physical concepts.

You have learned some of the mathematics that you need for this course and will be learning more about vectors and vector calculus soon. In this lesson, we will practice some of the mathematics. You will also prepare an Excel workbook that will help you with some of this course’s assessment problems.

Learning Objectives

By the end of this lesson, you should be able to:

• correctly use significant figures, dimensions, and units
• solve simple problems using integral and differential calculus
• prepare and use a course Excel workbook for course calculations 

Questions?

If you have any questions, please post them to the Course Questions discussion forum. I will check that discussion forum daily to respond. While you are there, feel free to post your own responses if you, too, are able to help out a classmate.

1.1 The atmosphere is …

The atmosphere is amazing, awe-inspiring, frightening, deadly, powerful, boring, strange, beautiful, and uplifting – just a few of thousands of descriptions. So much of our lives depend on the atmosphere, yet we often take it for granted.

Clouds over the Arctic Ocean at sunrise

Credit: W. Brune © Penn State is licensed under CC BY-NC-SA 4.0 [1]

Atmospheric science attempts to describe the atmosphere with physical descriptions using words, but also with mathematics. The goal is to be able to write down mathematical equations that capture the atmosphere’s important physical properties (predictability) and to use these equations to determine the atmosphere’s evolution with time (prediction). Predicting the weather has long been a primary focus, but, increasingly, we are interested in predicting climate.

We know quite a lot about the atmosphere. It has taken decades, if not centuries, of careful observation and insightful theory that is based on solid physical and chemical laws. We have more to learn. You could help to advance the understanding of the atmosphere, but you must first understand the physical concepts and mathematics that are already well known. That is a primary purpose of this course – to give you that understanding.

What follows, below, is a series of pictures and graphical images. Each one depicts some atmospheric process that will be covered in this course. Look at these images; you will see them again, each in one of the next ten lessons. Of course, in each observation there are many processes going on simultaneously. In the last lesson, you will have the opportunity to look at an observation and attach the physical principles and the mathematics that describe several processes that are causing the phenomena that you are observing.

1.2 You won’t believe what you can do with math!

You’ve been told many times that meteorology is a math-intensive field. It is. But for this course, you already know much of the math, and what you haven’t seen, you will see in vector calculus. To get ready for the meteorology and atmospheric science in this course, you will need to refresh your ability to solve simple math problems, including solving simple problems in differential and integral calculus. At the same time, we will remind you about the importance of correctly specifying significant figures and units in your answers to the problems. The goal of this first lesson is to boost your confidence in the math you already know.

How many figures should be in my answer?

Suppose you are asked to solve the following word problem:

In the radar loop, a squall line is oriented in the north-south direction and is heading northeast at 57 km hr^-1. In the last frame of the loop, the line is 17 km west of the Penn State campus. You are out running and know that you can make it back to your apartment in 25 minutes. Will you get back to your apartment before you get soaked?

You reason that the line is moving northeast, and thus, at an angle of 45^o relative to the east. Therefore, the eastward motion of the squall line is just the velocity times the cosine of 45^o. That gives you the eastward speed. You decide to divide the distance by the eastward speed to get the amount of time before the line hits campus. You plug the numbers into your calculator and get the following result:

$\text{time}=\frac{17\text{ km}}{\text{ (}57\text{ km/h)}\cdot \cos \left(\mathrm{45º}\right)}=0.42178\text{ hours}=25.3070\text{ minutes}$

According to your calculation, you will make it back with 0.3 minutes (18 seconds) to spare. But can you really be sure that the squall line will strike in 25.3070 minutes? Maybe you should figure out how many significant figures your answer really has. To do that, you need to remember the rules:

1.3 If you thought practice makes perfect, you could be right.

Calculus is an integral part of a meteorologist’s training. The ability to solve problems with calculus differentiates meteorologists from weather readers. You should know how to perform both indefinite and definite integrals. Brush up on the derivatives for variables raised to powers, logarithms, and exponentials. We will take many derivatives with respect to time and to distance.

Simple Integrals and Derivatives That are Frequently Used to Describe the Behavior of Atmospheric Phenomena

1. 

$$\begin{array}{l}\frac{da}{dt}=-ka\\ \frac{da}{a}=-kdt\\ {\displaystyle \underset{a_o}{\overset{a_1}{\int }}\frac{da}{a}}=-{\displaystyle \underset{t_o}{\overset{t_1}{\int }}kdt}\\ \ln (a_1)-\ln (a_0)=-k\left(t_1-t_0\right)\\ \ln (a_1/a_0)=-k\left(t_1-t_0\right)\\ a_1/a_0=e^{\left(-k\left(t_1-t_0\right)\right)}=\exp \left(-k\left(t_1-t_0\right)\right)\\ a_1=a_0{e}^{\left(-k\left(t_1-t_0\right)\right)}=a_0\exp \left(-k\left(t_1-t_0\right)\right)\end{array}$$

2.  $p=p_o{e}^{\left(-z/H\right)};{\displaystyle \underset{0}{\overset{\infty }{\int }}pdz=\text{? (Do the definite integral.)}}$

$${{\displaystyle \underset{0}{\overset{\infty }{\int }}pdz=-H{p}_o{e}^{-z/H}|}}_0^{\infty }=-H{p}_o\left(0-1\right)=p_{o}H$$

3.  $p=p_0{e}^{\left(-\frac{z}{H}\right)};\frac{1}{p}\frac{dp}{dz}=?$

$$\frac{dp}{dz}=-\frac{1}{H}{p}_0{e}^{\frac{-z}{H}}=-\frac{1}{H}p;\frac{1}{p}\frac{dp}{dz}=-\frac{1}{H}$$

4. $\begin{array}{l}\frac{d\ln (ax)}{dt}=?\frac{d\ln (ax)}{dt}=\frac{1}{ax}\frac{d(ax)}{dt}=\frac{1}{ax}\frac{adx}{dt}=\frac{1}{x}u\text{ , where u = velocity}\\ \end{array}$

5. $d(\cos (x))=?d(\cos (x))=-\sin (x)dx$

You have the power.

Often in meteorology and atmospheric science you will need to manipulate equations that have variables raised to powers. Sometimes, you will need to multiply variables at different powers together and then rearrange your answer to simplify it and make it more useful. In addition, it is very likely that you will need to invert an expression to solve for a variable. The following rules should remind you about powers of variables.

Are you ready to give it a try? Solve the following problem on your own. After arriving at your own answer, click on the link to check your work. Here we go:

1.4 Are you ready to get with the programming?

Meteorologists and atmospheric scientists spend much of their time thinking deep thoughts about the atmosphere, the weather, and weather forecasts. But to really figure out what is happening, they all have to dig into data, solve simple relationships they uncover, and develop new ways to look at the data. Much of this work is now done by programming a computer. Many of you haven’t done any computer programming yet, and for those of you who have, congratulations – put it to good use in this class. For those who are programming novices, we can introduce you to a few of the concepts of programming by getting you to use Excel or another similar spreadsheet program.

To help you learn and retain the concepts and skills that you will learn in this course, you will solve many word problems and simple math problems. For several activities, we give you the opportunity to practice solving particular types of problems enough times until you gain confidence that you can solve those same types of problems on a quiz. That means that you will be solving some types of problems several times and only the numbers for the variables will change. The simplest way for you to solve these problems is to program a spreadsheet to do that repetitive math for you.

Spreadsheet Screenshot 1

Credit: Image developed by W. Brune © Penn State with Excel [7]  2019 and licensed under CC BY-NC-SA 4.0 [8]

Click for a text description of the spreadsheet screenshot.

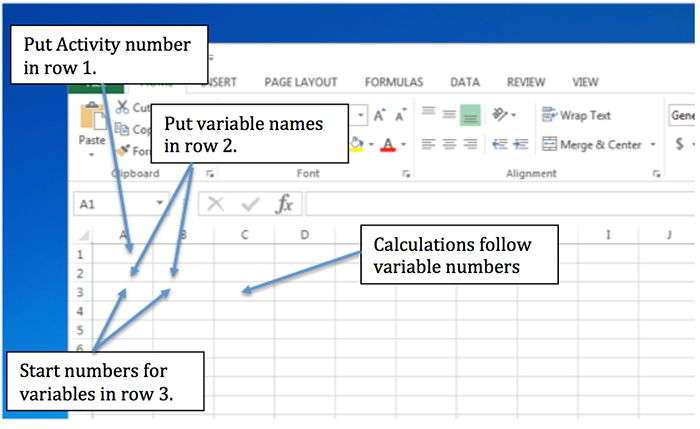
Screenshot shows an Excel Spreadsheet

A text box says "put activity number in row 1" and an arrow points to cell A1.

A second text box says "put variable names in row 2" with an arrow pointing to cells A2 and B2

A third text box says "start numbers for variables in row 3" with an arrow pointing to cells A3 and B3

A final text box says "calculations follow variable numbers" with an arrow pointing to C3.

Let’s do a simple example. Suppose we have several boxes, some with different shapes and sizes, and we want to calculate the volume of the boxes and find the total volume. I have put in the names of the variables (with units!) and then the numbers for the length, width, and height of each box type and the total number of each box. To calculate the volume of each box, click on E3 and put an “= a3*b3*c3” in the equation line. Hit enter and it will do the calculation and put the answer in E3. A small square will appear in the lower right corner of E3. Click on this square with the mouse and pull down over the next three rows. Excel will automatically do the calculations for those rows. To calculate the total volume, go to F3 and enter “=d3*e3,” and hit “enter.” Grab the small box and pull down to get the total volume of each type of box. To get the total volume, click on F7, click on “Formulas,” and then “AutoSum,” and finally “Sum.” Excel will show you which cells it intends to sum. You can change this by adjusting the edges of the box it shows. Finally, pay attention to significant digits in your calculated volumes. You can adjust the number of decimal places by highlighting a cell or group of cells and then by clicking on the appropriate icon on the Excel tool bar. Note that an incorrect number of significant figures is displayed in some of the answers--see if you can figure out where.

Spreadsheet Screenshot 2

Credit: Image developed by W. Brune © Penn State with Excel [7] 2019 and licensed under CC BY-NC-SA 4.0 [8]

Click for a text description of the spreadsheet example part 1.

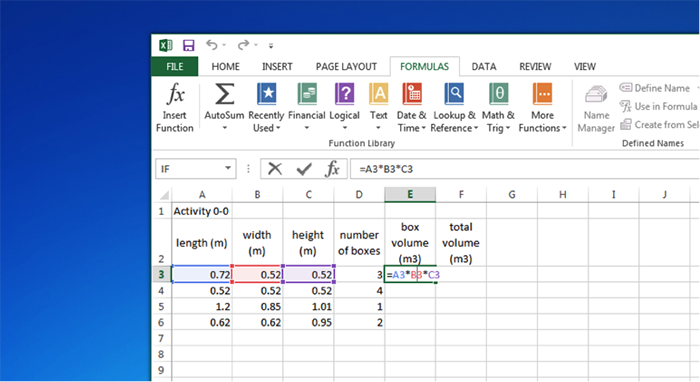
length (m)	width (m)	height (m)	number of boxes	box volume (m3)	total volume (m3)
0.72	0.52	0.52	3	=A3*B3*C3
0.52	0.52	0.52	4
1.2	0.85	1.01	1
0.62	0.62	0.95	2

Spreadsheet Screenshot 3

Credit: Image developed by W. Brune © Penn State with Excel [7] 2019 and licensed under CC BY-NC-SA 4.0 [8]

Click for a text description of the spreadsheet example part 2.

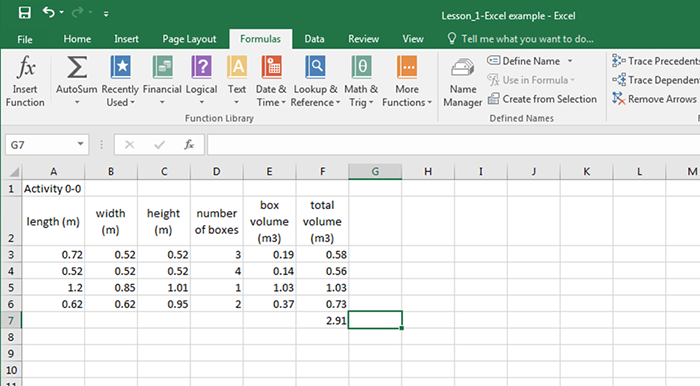
length (m)	width (m)	height (m)	number of boxes	box volume (m3)	total volume (m3)
0.72	0.52	0.52	3	0.19	0.58
0.52	0.52	0.52	4	0.14	0.56
1.2	0.85	1.01	1	1.03	1.03
0.62	0.62	0.95	2	0.37	0.73

Hopefully this example is a refresher for most of you. For those who are totally unfamiliar with Excel, please click on the question mark in the upper right of the screen and type in the box “creating your first workbook.” You can also visit Microsoft's help page for additional step-by-step instructions for how to Use Excel as Your Calculator [9]. The best way to learn, after the introduction, is by doing. The Keynote Support website [10] also lists helpful summaries of instructions.

Summary

There is a very good reason that you are taking this class and I am teaching it – all of us are fascinated by the weather, awed by the atmosphere’s power, and passionate about learning more about it. Quite honestly, I can’t imagine a more rewarding career than the one that you are embarking upon or the one that I have. Nothing could be more rewarding than saving lives by making the atmosphere more predictable or by making the perfect prediction. Nothing.

But, do you know what? The best forecasters are the ones who can not only read weather maps, but who also know physically what the atmosphere is doing. The best forecasters know how to translate the physics into mathematics so that hand-waving can be turned into usable numbers. This course will start to make all of these connections between observations and physical cause-and-effect and help us find numerical solutions to questions.

For those of you who are in related disciplines, this course will give you a solid basic understanding of the atmosphere that you can apply in your studies and career, whether it be civil engineering, mechanical engineering, environmental engineering, chemistry, hydrology, or many other fields. 

We have now reviewed some important concepts like significant figures and dimensions and units. You will continue to gain confidence in using the differential and integral calculus that you already know. As you go through the course, I want you to look back at the pictures of the atmosphere and imagine which equations are governing the processes that are causing your observations.

Reminder - Complete all of the Lesson 1 tasks!

You have reached the end of Lesson 1! Make sure that you have completed all of the tasks in Canvas.