Overview

Atmospheric radiation plays a critical role in life on Earth and in weather. Without solar heating, Earth would be a dead frozen ball hurtling through space. Luckily, the energy that Earth receives from solar radiation is sufficient to produce liquid water on its surface, thus enabling life to thrive. In this lesson we will look at solar radiation and its changes over time. Radiation is just another form of energy and can be readily converted into other forms, especially thermal energy, which is sometimes called "heat." In this lesson, we will use the word "radiation" to mean all electromagnetic waves, including ultraviolet, visible, and infrared radiation. We will introduce some unfamiliar terms like "radiance" and "irradiance" and will be careful with our language to prevent confusion.

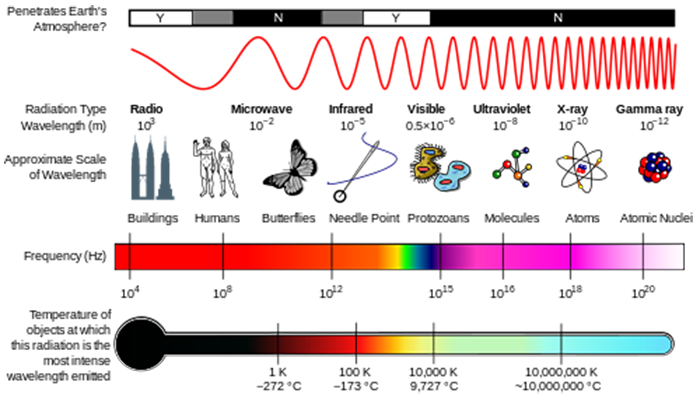
An important concept in studying atmospheric radiation is that all objects emit and absorb radiation. For a perfect emitter, the radiation emitted by an object, called the irradiance, is determined by the Planck function, which depends only on temperature and wavelength. The higher the temperature, the greater the radiation emitted at all wavelengths and the shorter the wavelength of the peak energy. The Sun emits mainly in the visible while Earth and its atmosphere emit mainly in the infrared. No object is really a perfect emitter at every wavelength; the unitless number emissivity measures how good or poor an emitter is. At each wavelength, a good emitter is a good absorber.

How well an object absorbs at different wavelengths of radiation, called its absorptivity, depends on its chemical composition and the rules of quantum mechanics. As a result, some absorption is strong and some is weak; some is in sharp lines while some is in broad features in the wavelength spectrum; some is in the UV, particularly due to O₂ and O₃, little is in the visible, and much absorption, including broad bands and sharp lines, occurs in the infrared, particularly by H₂O, CO₂, and O₃.

The radiation that is not absorbed by a gas, liquid or solid is either transmitted or scattered. The amount of transmitted radiation depends on the absorption and scattering cross sections of the gas, liquid, or solid components of matter, so that the larger the cross section and the distance through the matter, the less radiation passes through the matter. The decay of the transmitted light with distance through the matter is exponential, as is described by Beer’s Law.

Earth’s surface and atmospheric gases can emit and absorb radiation at the same wavelengths. Most of Earth’s emissions are at infrared wavelengths, whether the emission be from the surface, clouds, or atmospheric gases.

Scattering of atmospheric radiation complements absorption and is even more difficult to track through the atmosphere than absorption is. The wavelength of the radiation and the size, shape, and composition of the scattering particle together determine the scattering efficiency and scattering pattern. Many of the skies that we remember best are due to the scattering and absorption of sunlight.

Learning Objectives

By the end of this lesson, you should be able to:

• identify the causes of changing solar radiation on Earth
• calculate properties of the spectrum of solar and earth radiation in terms of the Planck function
• calculate the absorption between you and a light source
• explain why the sky looks blue and hazy in the summer

Questions?

If you have any questions, please post them to the Course Questions discussion forum. I will check that discussion forum daily to respond. While you are there, feel free to post your own responses if you, too, are able to help out a classmate.

6.1 Atmospheric Radiation: Why does it matter?

Everything radiates—the Sun, the Earth, the atmosphere, and you. The energy provided by the Sun is reused in the Earth system to provide the energy that drives weather and climate. But ultimately, the infrared radiation radiated by Earth into space must balance the solar visible radiation coming into the Earth system. From the point-of-view of the Earth system, we are most concerned about how atmospheric radiation interacts with matter. Matter is simply molecules and atoms and the structures that they build, such as the air, the clouds, the Earth, and the Sun. 

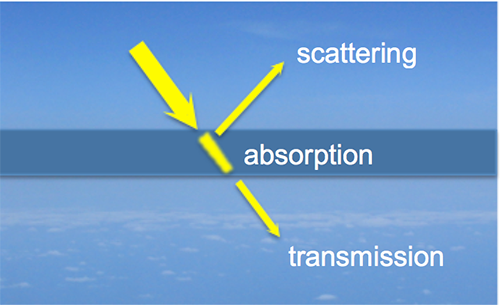
When radiation encounters matter, three things can happen. The radiation can be transmitted through matter; it can be absorbed by the matter; it can be scattered by the matter. One of these three things must happen, so we can sum them up to one:

where t is the transmissivity, the fraction of the radiation that is transmitted; a is the absorptivity, the fraction absorbed; and s is the reflectivity, the fraction that is scattered or reflected.

What can happen when radiation meets matter. The sum of radiant energy that is scattered, absorbed, and transmitted must equal the amount of incoming radiant energy.

Credit: W. Brune © Penn State is licensed under CC BY-NC-SA 4.0 [1]

6.2 Start at the Source: Earth Rotating Around the Sun

Solar radiation drives the Earth system and makes life possible. Solar radiation is absorbed and then put to use to increase the surface temperature, to change the phase of water, and to fuel atmospheric chemistry. The uneven distribution of solar radiation on Earth’s surface drives atmospheric dynamics.

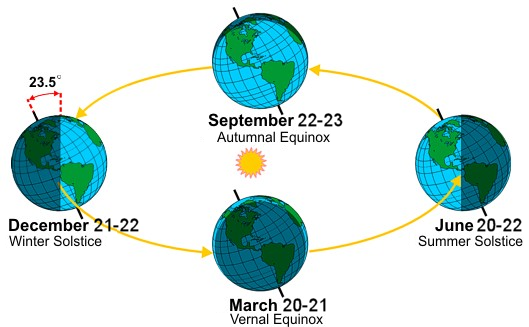
The total amount of solar energy per unit time and unit area, also called the solar irradiance, is 1361 W m^–2 at the top of the atmosphere (Stephens et al., 2012, Nature Geoscience 5, p. 691). It is distributed unevenly over Earth’s surface. That distribution changes over the course of the seasons (see next two figures). The seasons result primarily from the Earth's rotation axis not being perpendicular to the plane of the Earth's orbit around the Sun.

Earth’s orbit around the sun.

Credit: Credit: The Seasons. National Oceanic and Atmospheric Administration/National Weather Service [2]. (NOAA) (Public Domain)

The current tilt of Earth’s orbit. More solar radiation is absorbed by a square meter of Earth's surface near the equator than a square meter at high latitudes as a result of the curvature of the Earth.

Credit: National Park Service [3]. (NPS)

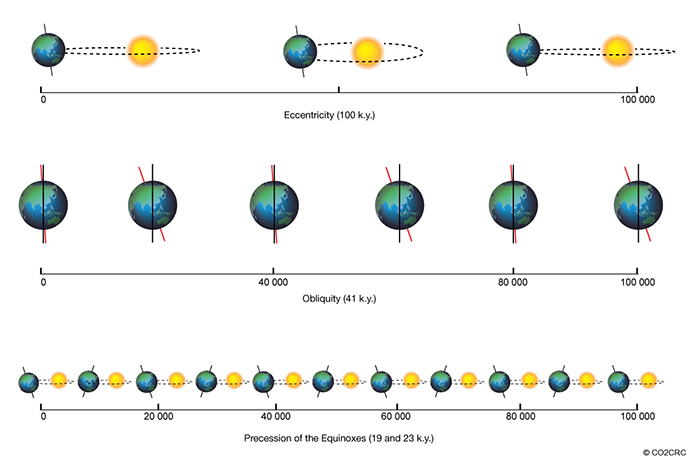
Earth’s spin and its orbit around the sun are not constant, but instead, change with time, like a spinning top. The orbit’s eccentricity (i.e., how different it is from circular) varies with a 100,000-year period. The tilt of Earth’s rotation axis with respect to a line perpendicular to the plane of Earth's orbit, which is called the obliquity, varies from 22.1^o to 24.5^o during a 41,000-year cycle. The obliquity is currently 23.4^o and decreasing. Finally, the precession of Earth’s orbit, which is the orientation of the rotation axis with respect to Earth’s orbital position, also varies with a period of about 26,000 years, although the orbit itself is also rotating around the sun, so that the effective period of precession is about 21,000 years. These motions, when taken together, slowly and periodically change the distribution of solar irradiance on Earth’s surface and are described by the Milankovitch Theory (see next two figures). The changes in solar radiation ultimately lead to very large changes in climate and greenhouse gas concentrations, particularly the ice ages, which occur about every 100,000 years. The greenhouse gas changes (methane and carbon dioxide, in particular) were presented in Lesson 4.

Changes in Earth’s orbit that occur over time (top). Eccentricity (non-circular shape) varies over 100,000 years (middle). Obliquity (tilt of Earth’s rotation axis) varies every 41,000 years (bottom). Precession (obliquity relative to position in Earth’s orbit) varies over a cycle with a period of approximately 20,000 years.

Credit: Credit: CO2CRC [4].

Variation of solar irradiance (i.e., forcing) observed as a result of the changes in eccentricity, obliquity, and precession. Links to glaciation are complex but the distribution of solar irradiance on Earth is important for climate.

Credit: Milankovitch Variations [5] from Wikimedia Commons [6] is licensed under CC BY-SA 3.0 [7]

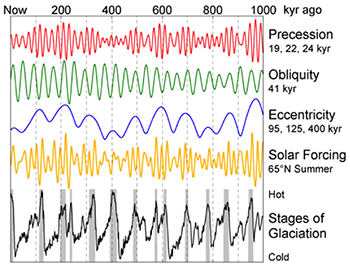
Changes in Earth’s orbit and spin are not the only ways that solar irradiance changes—the Sun’s energy output also changes. It has been increasing slightly (0.05–0.10%) over the past 300 years and varies by another ~0.1% over the course of the 11-year solar cycle. The ultraviolet (200–300 nm) irradiance has increased by about 3% in the past 300 years and varies by ~1.5% between solar maximum and solar minimum. This increased UV leads to greater stratospheric ozone production, which increases stratospheric heating, leading to the poleward displacement of the stratospheric meridional wind.

6.3 How is energy related to the wavelength of radiation?

We can think of radiation either as waves or as individual particles called photons. The energy associated with a single photon is given by $$ E = hν , where E is the energy (SI units of J), h is Planck's constant (h = 6.626 x 10^–34 J s), and $\nu$ is the frequency of the radiation (SI units of s^–1 or Hertz, Hz) (see figure below). Frequency is related to wavelength by $\lambda =c/\nu$ , where c, the speed of light, is 2.998 x 10⁸ m s^–1. Another quantity that you will often see is wavenumber, $\sigma =1/\lambda$, which is commonly reported in units of cm^–1.

The energy of a single photon that has the wavelength λ is given by:

Note that as the wavelength of light gets shorter, the energy of the photon gets greater. The energy of a mole of photons that have the wavelength λ is found by multiplying the above equation by Avogadro's number:

Energy scales: penetration through Earth’s atmosphere; radiation name by wavelength; physical object the size of that wavelength; frequency compared to wavelength; and temperature of an object that has its peak radiation at each wavelength.

Credit: Credit: EM Spectrum Properties reflected [8] by Inductiveload from Wikimedia Commons [6] is licensed under CC BY-SA 3.0 [7].

In the lesson on atmospheric composition, you saw how solar UV radiation was able to break apart molecules to initiate atmospheric chemistry. These molecules are absorbing the energy of a photon of radiation, and if that photon energy is greater than the strength of the chemical bond, the molecule may break apart.

6.4 The Solar Spectrum

The Sun's emission in the extreme ultraviolet part of the solar emission spectrum.

Credit: NASA Goddard Space Flight Center [9] via flickr

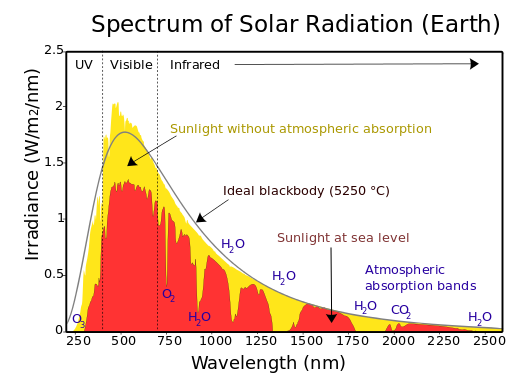
The Sun emits radiation from X-rays to radio waves, but the irradiance of solar radiation peaks in the visible wavelengths (see figure below). Common units of irradiance are Joules per second per m² of surface that is illuminated per nm of wavelength (e.g., between 300 nm and 301 nm), or W m^–2 nm^–1 for the plot below. These units are the units of spectral irradiance, which is also simply called irradiance, but as a function of wavelength. To get the total irradiance in units of W m^–2, the spectral irradiance should be integrated over all the wavelengths.

Note the following for the solar spectrum:

• About half of the energy is in the visible wavelengths below 0.7 μm. We can tell this by doing a quick integration.
• O₃ and O₂ absorb much of the UV irradiance below 300 nm high in the atmosphere.
• About 70% of the visible irradiance makes it all the way to sea level.
• O₃ absorbs a little of the visible irradiance.
• A significant fraction of the visible irradiance is scattered by clouds and aerosol. Some is reflected back out into space so that this portion never deposits energy in the Earth system.
• There are large wavelength bands in which water vapor, CO₂, and O₃ absorb infrared irradiance.

For solar wavelengths at which the absorptivity is high, the solar irradiance at sea level is small. Note that the big absorbers of infrared irradiance are water vapor, carbon dioxide, and ozone.

Solar spectrum and atmospheric absorbing gases from 240 nm to 2.5 µm wavelengths.

Credit: Nick84 [CC BY-SA 3.0 [7]], via Wikimedia Commons

6.5 What is the origin of the Planck Function?

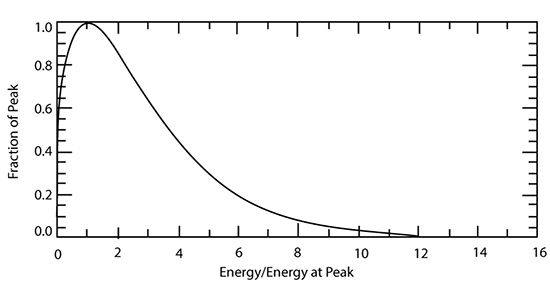
Recall that molecules have a wide range of speeds and thus a wide range of energies. The Maxwell–Boltzmann Distribution, which gives the distribution of molecules as a function of energy, is given approximately by the equation:

where f is the probability that a molecule has an energy within a small window around E, T is the absolute temperature, and k is the Boltzmann constant. The above equation, when integrated over all energies, gives the value of 1.

The functional form of this distribution is shown below:

Maxwell–Boltzmann distribution of molecules as a function of the energy of the molecules normalized to the number of molecules with the peak energy.

All objects—gas, liquid, or solid—emit radiation. If we think of radiation as photons, we would say that these photons have a distribution of energies, just like molecules do. However, photons cannot have continuous values of photon energy; instead, the photon energy is quantized, which means that it can have only discrete energy values that are different by a very very small amount of energy. When this quantized distribution is assumed, then the distribution of spectral irradiance leaving a unit area of the object’s surface per unit time per unit wavelength interval into a hemisphere is called the Planck Distribution Function of Spectral Irradiance:

where h is Planck’s constant, c is the speed of light, k is the Boltzmann constant (1.381 x 10^–23 J K^–1), T is the absolute temperature, and λ is the wavelength. The integral of this function over all wavelengths leads to the Stefan–Boltzmann Law Irradiance, which gives the total radiant energy per unit time per unit area of the object’s surface emitted into a hemisphere.

P_e(λ)/π is called the Planck Distribution Function of Spectral Radiance and commonly has units of W steradian^–1 m^–2 nm^–1 and is often denoted by the letter I. A steradian is just a unit solid angle. Just as a radian for a circle is a length of the circle's arc that is equal to the circle's radius, a steradian is the area on a sphere's surface that is equal to the sphere's radius squared. There are 2π radians along a circle and 4π steradians (abbreviated sr) over a sphere. For some of this discussion we will use the spectral irradiance P_e(λ) and consider the radiation from any area on the sphere to be emitted not in a single direction but into the full hemisphere of directions. Later on, when we start talking about absorption, we will need to think about the irradiance in very specific directions, in which case we will use radiance. Be mindful of the difference between irradiance and radiance.

The spectral irradiance is the amount of energy that is emitted from or falling on a unit area in space per unit time per unit wavelength (W m^–2 µm^–1). So the m² in this case indicates a surface area on which energy is leaving or falling. To get the Sun’s spectral irradiance at the top of Earth’s atmosphere, we must multiply the spectral irradiance emitted by the Sun's surface by the Sun's surface area to get the total energy emitted per unit time and per unit wavelength by the Sun and then divide by the surface area of the sphere that has a radius equal to the Earth–Sun distance to get the energy per time per unit wavelength per unit area of the surface located at the top of Earth's atmosphere.

Physical Interpretation

All the radiation that is emitted from the Sun’s surface continues to move outward at the speed of light until it hits objects, but there are very few objects between the Sun and Earth, except occasionally the Moon. Thus, in the absence of any objects, the total amount of solar irradiance striking the planets decreases as the square of the distance between the center of the Sun and the surface of the planet.

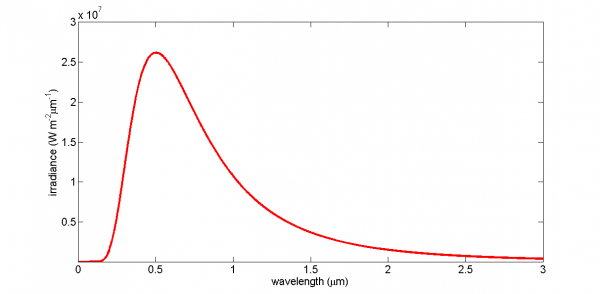
The Planck distribution function spectral irradiance for an object at a temperature of 5777 K (the Sun's surface temperature) is shown in the figure below. Note the rapid rise at the shorter wavelengths, the peak value, and then the slower decline at longer wavelengths. Look at the peak value of the irradiance, which is about 25 million W m^–2 nm^–1! That's a lot of energy being radiated from the Sun's surface, but of course the Earth is 150 million km away from the Sun and thus intercepts less than half a billionth of the solar irradiance.

The Planck distribution function spectral irradiance, P_e (equation 6.4) emitted into a hemisphere for the Sun's surface temperature, T_sun = 5777 K.

Credit: W. Brune

6.6 Which wavelength has the greatest spectral irradiance?

The peak of this distribution as a function of wavelength can be found by taking the derivative of P_e(λ) with respect to wavelength, setting the value equal to 0, and solving for the wavelength. The result is the Wien Displacement Law:

For the sun with a photospheric temperature of about 5780 K, λ_max ~ 0.500 μm or 500 nm, which is the color green. However, for Earth with a mid-tropospheric temperature of about 260 K, the peak wavelength is closer to 11 μm, well into the infrared (see below). 

The spectral irradiance of solar radiation for a surface located at the top of Earth's atmosphere (red solid curve) and the spectral irradiance emitted by Earth into the upward hemisphere above its surface (blue dashed curve) To get these curves, we assumed that the Sun and the Earth both emit radiation according to the Planck distribution function spectral irradiance, which they do not quite do.

Credit: W. Brune

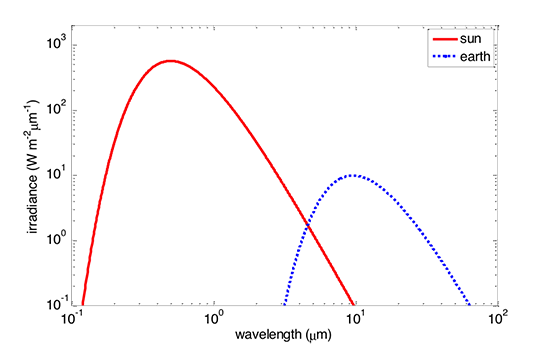
6.7 What is the total irradiance of any object?

If the Planck distribution function spectral irradiance is integrated over all wavelengths, then the total irradiance emitted into a hemisphere is given by the Stefan–Boltzmann Law:

where σ is called the Stefan–Boltzmann constant (5.67 x 10^–8 W m^–2 K^–4). F_s has SI units of W m^–2, where the m² refers to the surface area of the object that is radiating.

The Stefan–Boltzmann law (total) irradiance applies to an object that radiates according to the Planck distribution function spectral irradiance. If we look at the figure below, we see that the solar spectrum at the top of the atmosphere is similar to the Planck distribution function but does not follow it perfectly. However, the Planck distribution function with the same total irradiance as the sun has a temperature of 5777 K, as in the second figure.

Solar spectrum and atmospheric absorbing gases from 240 nm to 2.5 µm wavelengths.

Credit: Nick84 [CC BY-SA 3.0 [7]], via Wikimedia Commons

The Planck distribution function spectral irradiance, P_e (equation 6.4), emitted into a hemisphere for the sun, T_sun = 5777 K.

Credit: W. Brune

Check Your Understanding

Clouds radiate. Assume two spherical clouds, one with a radius of 100 m and a temperature of 275 K and a second with a radius of 100 m and a temperature of 230 K. Assuming that they both radiate according to the Planck distribution function, calculate the emission for each cloud in W m^–2 and in W. Which cloud is radiating more total energy and by how much?

Click for answer.

ANSWER:

Cloud T (K)	Cloud radius (m)	Fs (W m–2)	Fs x 4πRc2 (W)
275	100	324	4.1 x 107
230	100	159	2.0 x 107

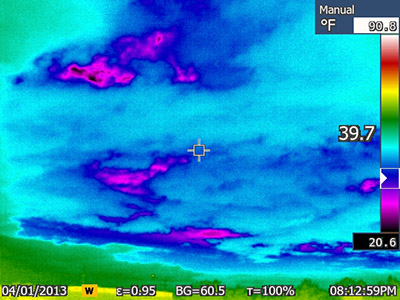
The warmer cloud is radiating about twice as much energy as the cooler cloud. These little clouds are radiating quite a lot of energy in all directions, but some of it is down toward Earth’s surface. If we make the simple assumption that half the radiation goes up and the other half goes down, the amount of energy radiated toward Earth’s surface per second is approximately 10 million W. If the clouds are not too far from the surface, this downward radiation could contribute a few hundred W m^–2 of heating at Earth’s surface. Thus clouds can act like additional heat sources for Earth’s surface, keeping its temperature higher than it would be on a clear night. The image below is an infrared photograph of the sky above Ogden, Utah. Infrared radiation detected by the camera has been converted to temperature, with higher temperatures indicating more infrared emission.

Credit: activerain [10]

6.8 Kirchhoff’s Law explains why nobody is perfect.

Remember that when radiation encounters matter it may be absorbed or transmitted or scattered (including reflected). For an object acting as a perfect Planck distribution function, it must absorb all radiation completely with no scattering and no transmission. Some objects absorb very well at some wavelengths but not at others. For instance, water vapor absorbs little visible radiation but absorbs infrared radiation at some wavelengths very well.

At the same time, the sun, like other objects, does not radiate perfectly according to the Planck distribution function spectral irradiance, but instead radiates at a fraction of it at some wavelengths. This fraction, which goes from 0 to 1, is called the emissivity and is denoted by ε. How is an object’s emissivity related to its absorptivity?

Kirchhoff’s Law states that at any given wavelength, an object’s emissivity ε is equal to its absorptivity, that is:

where we understand that ε is some form of averaged emissivity.

Watch the following video (1:07), where the Stefan–Boltzmann Law is described in greater detail:

What about gases? Gases absorb and thus emit like all other matter. To know more about the emissivity of all objects, we need to know more about the absorption of objects.

6.9 Why do objects absorb the way that they do?

The atmosphere absorbs a significant amount of radiation in the infrared but rather little in the visible. Also, we see that gases absorb strongly at some wavelengths and not at others. Why is this?

To answer this question, we need to look at the configurations of the electrons that are zooming around atoms and molecules. More than 100 years ago, scientists began using prisms to disperse the light from the sun and from flames containing different elements. While the sun gave the colors of the rainbow, the flames had light in very distinct lines or bands. This puzzle was finally resolved a little more than 100 years ago with the invention of quantum mechanics, which basically says that the electrons zooming around atoms and molecules and the vibrations and rotations of molecules can have only discrete energies that are governed by rules of conservation of angular momentum.

Perito Moreno Glacier Opal Iceberg in Argentina. The blue color results from selective absorption of radiation with wavelengths at the red end of the visible spectrum. In the figure below that shows the wavelength dependence of absorption by different molecules, you can see that water vapor has absorption in the red part of the visible spectrum, starting at about 600 nm (0.6 µm).

Credit: Dominic Alves [11] via flickr

The following bulleted list is a crash course in absorption by the electrons in atoms and molecules. Refer to the figure below the box.

The absorption cross section, σ, varies significantly over the width of the absorption line. So it is possible for all the radiation to be absorbed in the middle of the line but very little absorbed in the “wings.”

An energy level diagram for a molecule. The greater the distance between lines, the greater the energy of the absorbed or emitted photon and thus the shorter the photon’s wavelength. Not all transitions are allowed between all levels because of the conservation of angular momentum.

Credit: UC Davis chemwiki [12]

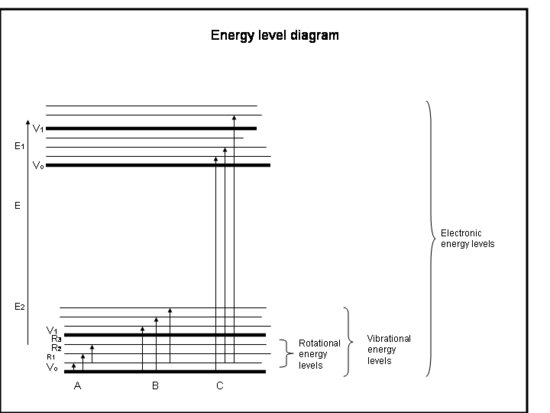
Physical Interpretation

Atoms and molecules can absorb radiation (a photon) only if their structure has an energy difference between levels that matches the photon’s energy (hc/λ). Otherwise, the atom or molecule will not absorb the light. Once the molecule has absorbed the photon, it can either lose a photon and go back to its original lower energy level; or it can break apart if the photon energy is greater than the chemical bond holding the molecule together; or it can collide with other molecules, such as N₂ or O₂, and transfer energy to them while it goes back to its lower energy level. Collisions happen often, so the energy of the absorbed photon is often transferred to thermal energy.

Calculated solar and terrestrial irradiances in the atmosphere. Gases considered for absorption are water vapor, carbon dioxide, oxygen, ozone, and nitrous oxide. Scattering is due to all gases (but mainly nitrogen and oxygen). The top panel shows the downgoing solar radiation at the Earth's surface (black line with red filling) and the upgoing terrestrial radiation at the top of the atmosphere (black line with blue filling). Also shown in the top panel are the Planck spectral irradiances for representative solar and terrestrial temperatures. Note that all curves in the top panel have been scaled such that the peak values are roughly the same. The middle panel shows the total extinction (due to absorption and scattering) by gases in the atmosphere. The bottom panel show the absorptivity of the individual gases and the scattering.

Credit: Robert A Rohde, Global Warming Art, via Wikimedia Commons [13]

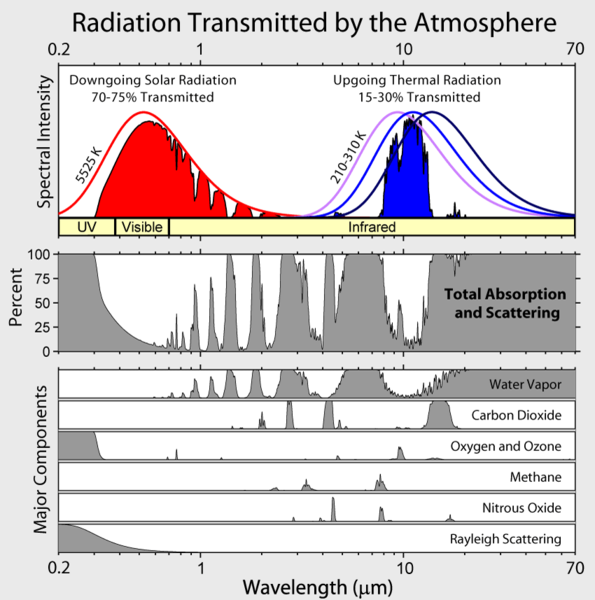
Note that Earth's outgoing infrared irradiance is limited to a few atmospheric "windows" and the irradiance at all other wavelengths is strongly absorbed, mostly by water vapor, but also by carbon dioxide, ozone, nitrous oxide, methane, and other more trace gases that aren't shown in the figure above.

6.10 How much radiation is absorbed as radiation passes through matter?

Gases, liquids, and solids can all absorb radiation. Since we are most interested in gases, we will use a gas to develop the equation that we need for absorption.

Suppose we have a volume of uniformly distributed gas that absorbs. Let's suppose that there is a beam of radiation that passes into this medium. Let's narrow this beam down so that all the radiation is traveling in essentially the same direction, so now we are interested in the irradiance that is traveling in a narrow range of angles, which is called the radiance, which is denoted by I and has units of W m^–2 steradian^–1 nm^–1. Refer back to Lesson 6.5 [14] to refresh your memory about what steradians are.

In an infinitesimal slab of that medium, a certain fraction dI of the radiation with radiance I (W m^–2) is absorbed. dI is equal to the absorption cross section, σ (m²), of a single molecule or particle multiplied by the number density, n (# m^–3) of absorbers, the length of the light-path through the slab, ds (m), and the amount of radiance I itself :

Note that both I and σ are functions of wavelength. If there is a beam of radiation with a certain wavelength, then the chance of absorbing the radiation depends on the cross-sectional area of each molecule or particle, which quantifies the efficiency with which the molecule absorbs the radiation with that particular wavelength. The absorption cross sections are largest if the energy of the radiation's wavelength matches the transition energy of an electron, atom, or molecule.

Integrating this expression over the total thickness of the volume, we get the Beer–Lambert Law:

$$I\left(\lambda \right)=I_o\left(\lambda \right)\exp \left[-\sigma \left(\lambda \right)ns\right]$$

where I_o is the radiance at the front edge of the path and I is the radiance at distance s along the path. Sometimes, we substitute a variable κ_a, called the absorption coefficient, for the product σn. In fact, you will see the absorption coefficient reported many ways.

When σns = 1, I(λ)/I_o(λ) = exp(–1) = 0.368.

For a uniform gas, the optical depth equals σns and is often given by the symbol τ (tau). If the optical depth gets large, then very little radiation gets through.

Example of Beer–Lambert Law: Laser light shining into a solution of a dye (Rhodamine 6B), which converts the green radiation to yellow radiation by a process called fluorescence. The yellow beam becomes weaker as it passes through solution because the green radiation that is making the dye fluoresce is being absorbed according to the Beer–Lambert Law.

Credit: Wikipedia [15]

Once we know the absorption coefficients of all of the absorbing molecules between the sun and the air volume of interest and the number densities of the absorbers, we can determine how much radiation will be absorbed at every wavelength.

The angle of the Sun with respect to the zenith (directly overhead) is called the solar zenith angle (SZA) and is 0^o overhead and 90^o on the horizon. The SZA affects the total path through absorbers, and thus is important. We often make an assumption that the atmosphere is a parallel plane (see figure below).

Schematic of the increase in path length with solar zenith angle as solar radiation passes through a layer, since ds > dz.

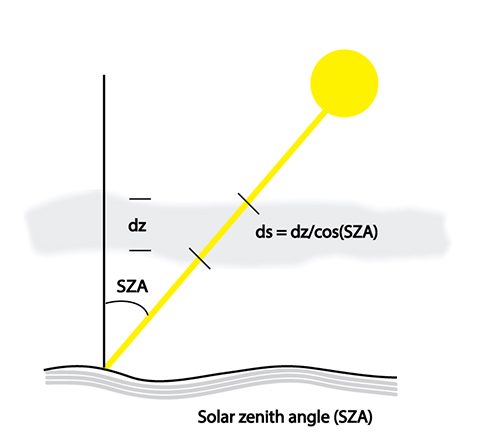
The result is that we can write $ds=\frac{1}{\cos \left(SZA\right)}dz=\sec \left(SZA\right)dz$ in the differential form of Beer's Law:

which gives:

Often, the integral is called the optical thickness, or optical path, where s₁ is one point along the path and s₂ is another. The exponential of the optical thickness, factoring in the sec(SZA), equals exp[–sec(SZA) τ(s₁,s₂)] and is called the transmittance, often designated with the symbol t, where τ is the optical depth.

For matter that absorbs and does not scatter, the absorptivity, a = 1 – t. Note that in this case the emissivity ε = a = 1 – t.

Usually, but not always, σ is a function of altitude because it often is a function of pressure and temperature, which vary for different altitudes.

Here is a video (2:03) further explaining Beer's Law:

6.11 What happens when we have both absorption and emission in the infrared?

Absorption and scattering apply to infrared radiation, just as they do to UV, visible, and microwave radiation. However, all matter that is at Earth-like temperatures is radiating in the infrared but isn’t hot enough to radiate significantly in the visible.

Remember that the peak in the Planck distribution function for a body at T = 300 K is given by Wien's Law:

To examine how extinction and emission work together, consider the case of an absorbing atmosphere with no scattering at a fixed wavelength. Assume that there is an absorbing gas between us and some radiation source which has a radiance I. Then I will be reduced as it travels through the absorbing gas:

But, at the same time, the layer with width ds is emitting:

Normally, we would multiply P_e by the emissivity for that wavelength. But because the absorptivity = emissivity for any given wavelength and type of matter by Kirchhoff’s Law, we can replace the emissivity, ε, with the absorptivity, κ_ads. Thus:

This equation is called Schwarzschild’s Equation. Please watch the video below (2:29).

NOAA GOES satellite measurement of water vapor using the 6.5–7.0 μm wavelength band, which is strongly absorbed by water vapor.

Credit: NOAA [16]

Physical Meaning

At every infrared wavelength, the change in the irradiance is due to the absorption of irradiance coming from some source, F, and the emission of irradiance by the absorbing gas itself. If the source is relatively strong (i.e., it produces a spectral irradiance greater than the Planck distribution function spectral irradiance from the gas), then the change in F will decrease mainly according to the Beer–Lambert Law. However, if the source is relatively weak, then the irradiance that gets to us will be due mostly to the gas itself.

Let’s look at this problem another way. Suppose we have an infrared sensor and are pointing it at the Sun. The Sun radiates some energy in the infrared, but at some wavelengths the water vapor and carbon dioxide are also radiating and the sensor may be picking up their irradiance. So what is the infrared sensor seeing?

Break the atmosphere into very thin layers, so thin that the temperature and amount of water vapor and carbon dioxide is almost constant over the thickness of each layer. Start with the layer closest to the sensor. It radiates both down to the sensor but also up to the layers above it. Since this first layer is just above us, the sensor measures the infrared radiation from it.

The next layer may be at a different temperature, but it too is radiating both down and up. Some of the irradiance in this second layer might get absorbed in the first layer depending upon what the first layer’s absorptivity is. If this absorptivity is a lot, then very little of the infrared radiation from the second layer will get through the first layer, according to the Beer–Lambert Law, but at the same time, the emissivity of the first layer will be great, so the irradiance of the first layer will be close to that of the Planck distribution function spectral irradiance at the layer’s temperature. As a result, the sensor will see mostly the first layer and not the second. If, on the other hand, the first layer has low absorptivity and thus low emissivity, then irradiance from the first layer to the sensor will be weak and irradiance from the second layer will get to the sensor along with irradiance from the first layer.

If we add a third layer, it too will be radiating the same amount of energy both down and up. Some or all of its irradiance might be absorbed in the first and second layers, so depending on the absorptivity of the first two layers, the sensor may or may not see any irradiance from the third layer.

You can see how we can build a model of atmospheric radiation by stacking individual layers with distinct amounts of water vapor and carbon dioxide on top of each other, one at a time, and as we add each one, use the Beer–Lambert Law to determine how much radiation from one layer is absorbed by the layers below or above it.

6.12 What about scattering?

Besides being absorbed or transmitted, radiation can be scattered. The scattering can be by particles of all sizes and by molecules. We can talk about the extinction of radiation by a particle that both absorbs and scatters.

When we have absorption and scattering by particles or molecules, we simply replace the absorption cross section with the extinction cross section in Equations 6.9 to 6.13 (see section 6.10).

Scattering is messy!!!! While absorption simply removes photons, or energy, from a beam of radiation, scattering can redirect the beam of radiation into other directions, where it can be absorbed or scattered some more. Furthermore, the intensity of the scattered radiation in different directions depends strongly on the radiation's wavelength and on the size, shape, and composition of the “particle,” where we can consider a molecule to be a particle.

A very important parameter is called the size parameter:

where r is the radius of a spherical particle and λ is the radiation’s wavelength.

Graph of size parameter x and type of scattering as a function of radiation wavelength and particle radius. Radiation and particle types are shown at the right and top, respectively.

Credit: W. Brune (after Grant Petty)

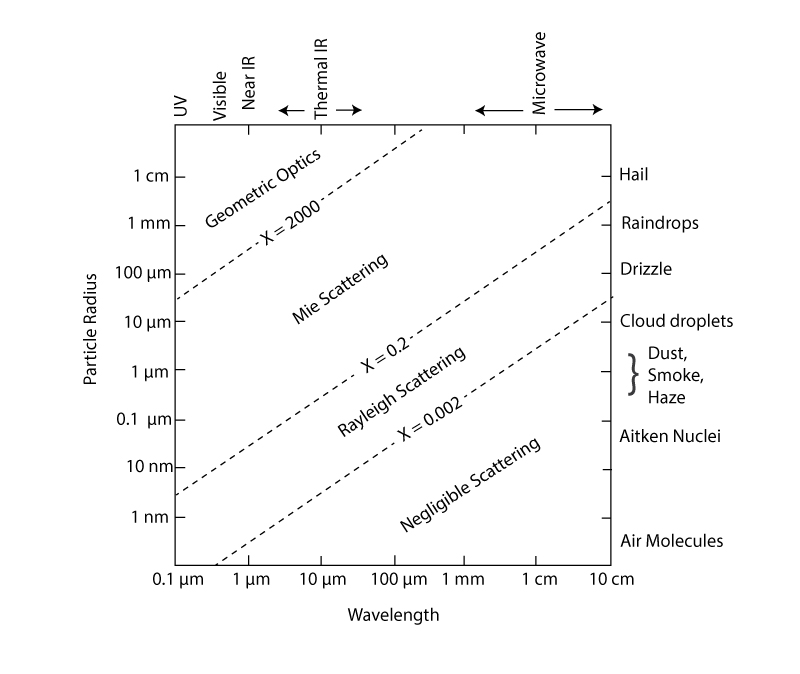
The effectiveness of scattering depends on the size parameter, which separates different types of scattering. For x > 2000, we have geometric optics. Geometric optics is when the particles get so big relative to the wavelength that we can calculate the interaction of radiation with them using optical principles (think of a lens or prism). For x = 0.2 to 2000, we have Mie scattering. Mie scattering is when the particle size is comparable to the size of the radiation wavelength, such as many atmospheric particles and light, from UV to microwave. For x between 0.002 and 0.2, we have Rayleigh scattering. Rayleigh scattering occurs for particles that are smaller than the radiation’s wavelength. This is the regime for molecules for the UV into the visible and for drizzle and raindrops for radar. Let’s look at its properties.

Scattering patterns by spheres for different values of the size parameter x. The source is on the left so that radiation is traveling from left to right. Note how the larger the particle radius is compared to the radiation wavelength, the more the radiation is scattered in the forward direction. The scattering of radiation by molecules or particles is most efficient for radiation that has a wavelength equal to the radius of the molecule or particle. Below that wavelength, the scattering is very inefficient, while above that wavelength, the scattering is efficient but not as much as when the wavelength equals the particle radius.

Credit: W. Brune (after Born and Wolf)

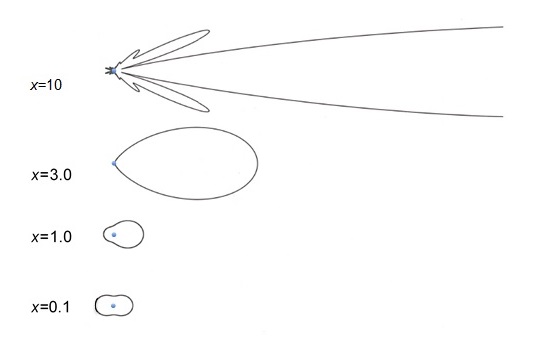
Without going through the math or the reasoning, I will state only that the scattering cross section for a molecule, particle, or raindrop in the Rayleigh regime (x << 1) is proportional to the sixth power of the particle radius and fourth power of the radiation wavelength.

In the Rayleigh regime, this scattering is equally strong in the backward and forward directions, with slightly less scattering in other directions (see figure above).

This strong wavelength dependence of scattering by small particles includes molecules at the wavelengths of visible radiation. This wavelength dependence of scattering leads to the preferential scattering of blue solar radiation compared to red solar radiation, which contributes to the blue of the sky in directions away from the sun and the deep orange-to-red colored sun as it sets. The image below shows both effects in one picture—a yellow-orange sunset below the cloud and a bright blue sky above the cloud.

For radar wavelengths, the r^₆ dependence of scattering by cloud and rain drops leads to much stronger back scattering of the radar beam with increasing drop size, thus allowing for estimates of raindrop sizes and thus rainfall rates.

Sunset on a partly cloudy day

Credit: W. Brune

See below for a video (2:09) explaining scattering in greater depth:

Summary

This lesson provided you with a basic understanding of atmospheric radiation. You should now be familiar with the following basic concepts:

• when radiation encounters matter, it can only be transmitted, absorbed, or scattered
• solar variability
• all objects are emitting radiation all the time
• emissivity = absorptivity at the same wavelength
• the molecular cause of absorption of different wavelengths of radiation by objects of different chemical composition
• Beer’s Law, which quantifies how much radiation will be absorbed as atmospheric radiation travels through an absorbing medium
• Schwarzschild’s equation, which quantifies the change in radiant energy per distance traveled through an emitting medium due to emission by layers and absorption of those emissions by layers above and below it, which are also emitting
• the dependence of the behavior of scattering on the wavelength of the radiation and the size of the scattering object

We will use many of these concepts in the next lesson on Applications of Atmospheric Radiation, in which we will consider two cases important to the atmosphere and weather: Earth’s radiant energy balance and Earth observed in the infrared by satellites in space.

Reminder - Complete all of the Lesson 6 tasks!

You have reached the end of Lesson 6! Double-check that you have completed all of the activities before you begin Lesson 7.