3.3 Phase Diagram for Water Vapor: Clausius Clapeyron Equation
3.3 Phase Diagram for Water Vapor: Clausius–Clapeyron Equation
The Clausius–Clapeyron Equation
We can derive the equation for es using two concepts you may have heard of and will learn about later: entropy and Gibbs free energy, which we will not go into here. Instead, we will quote the result, which is called the Clausius–Clapeyron Equation,
where lv is the enthalpy of vaporization (often called the latent heat of vaporization, about 2.5 x 106 J kg–1), Rv is the gas constant for water vapor (461.5 J kg–1 K–1), and T is the absolute temperature. The enthalpy of vaporization (i.e., latent heat of vaporization) is just the amount of energy required to evaporate a certain mass of liquid water.
What is the physical meaning? The right-hand side of [3.9] is always positive, which means that the saturation vapor pressure always increases with temperature (i.e., des/dT > 0). This positive slope makes sense because we know that as water temperature goes up, evaporation is faster (because water molecules have more energy and thus a greater chance to break the bonds that hold them to other water molecules in a liquid or in ice). At saturation, condensation equals evaporation, and since evaporation is greater, condensation must be greater as well. Much of the higher condensation comes from having more water vapor molecules hitting the liquid surface, which according to the Ideal Gas Law, means that the water vapor pressure is higher.
The temperature sensitivity of es is quite high. Plugging in the appropriate values to the right side of [3.9] yields 0.07 K–1, which means that the saturation vapor pressure increases by 7% for every 1 K increase in temperature. This high sensitivity has profound implications for weather and climate.
Separating variables (es and T) in [3.9] and integrating, assuming that lv is a constant with temperature (it is not quite constant!), yields:
Generally To is taken to be 273 K and eso is then 6.11 hPa.
Notes:
- es depends only on T, the absolute temperature. It is essentially independent of the atmospheric pressure, or any other factors.
- lv is not constant with temperature but instead changes slightly (from 2.501 x 106 J kg–1 at 0 oC to 2.257 x 106 J kg–1 at 100 oC).
- Thus, the most accurate forms of the integrated Clausius–Clapeyron Equation are more complicated but easy to deal with when using a computer.
What does the plot of this equation look like?
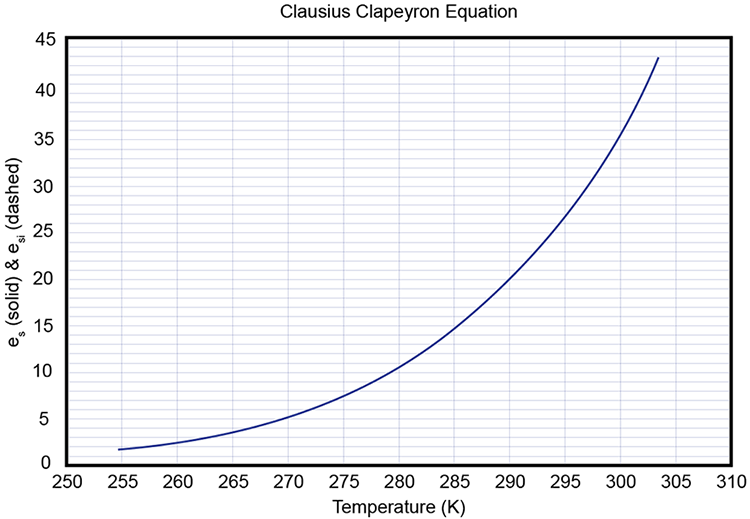
What happens between vapor and ice? The same methods can be applied and the same basic equations are obtained, except with a different constant:
where esi is the saturation vapor pressure for the ice vapor equilibrium and ls is the enthalpy of sublimation (direct exchange between solid water and vapor = 2.834 x 106 J kg–1).
Equations for es and esi that account for variations with temperature of lv and ls, respectively, can be found in Bohren and Albrecht (Atmospheric Thermodynamics, Oxford University Press, New York, 1998, ISBN 0-19-509904-4):
Dewpoint Temperature as a Measure of Water Vapor
Simply put, the dewpoint temperature is the temperature at which the atmosphere’s water vapor would be saturated. It is always less than or equal to the actual temperature. Mathematically,
which means that the water vapor pressure at some temperature T (not multiplied by T) equals the water vapor saturation pressure at the dewpoint temperature, Td. So we see that because ws depends only on Td at a given pressure, Td is a good method for designating the absolute amount of water vapor.
The Phase Diagram for Water
We can draw the phase diagram for water. There are three equilibrium lines that meet at the triple point, where all three phases exist (es = 6.1 hPa; T = 273.14 K). Along the line for es, vapor and liquid are in equilibrium, and evaporation balances condensation. Along the line for esi, vapor and ice are in equilibrium and sublimation equals deposition. Along the line for esm, liquid and ice are in equilibrium and melting balances fusion.

Is it possible to have water in just one phase? Yes!
The simplest case is when all the water is vapor, which occurs when the water vapor pressure is low enough and the temperature (and thus saturation vapor pressure) is high enough that all the water in the system is evaporated and in the vapor phase.
Let’s think about what it would take to have all the water in the liquid phase. Suppose we have a vertical cylinder closed on one end and a sealed piston at the other end. The whole cylinder is immersed in a constant-temperature water bath so that we can hold the cylinder and its contents at a fixed temperature (i.e., isothermal). Initially we fill the cylinder with liquid water and have a small volume of pure water vapor at the top. If we set the bath temperature to, say, 280 K and let the system sit for a while, the vapor will become saturated, which is on the es line. For isothermal compression, in which energy is removed from the system by the bath in order to keep the temperature constant, a push on the piston will slightly raise the vapor pressure above es and there will be net condensation until equilibrium is obtained again. If we continue to slowly push in the piston, eventually all the cylinder’s volume will be filled with liquid water and the cylinder will contain only one phase: liquid. If we continue to push the piston and the bath keeps the temperature constant, then the water pressure will increase.
In the atmosphere, ice or liquid almost always has a surface that is exposed to the atmosphere and thus there is the possibility that water can sublimate or evaporate into this large volume. Note that the presence or absence of dry air has little effect on the condensation and evaporation of water, so it is not the presence of air that is important, but instead, it is the large volume for water vapor that is important.
Conditions can exist in the atmosphere for which the water pressure and temperature are in the liquid or sometimes solid part of the phase diagram. But these conditions are unstable and there will be condensation or deposition until the condensation and evaporation or sublimation and deposition come into equilibrium, just as in the case of the piston above. Thus, more water will go into the liquid or ice phase so that the water vapor pressure drops down to the saturation value. When the water pressure increases at a given temperature to put the system into the liquid region of the water phase diagram, the water vapor is said to be supersaturated. This condition will not last long, but it is essential in cloud formation, as we will see in the lesson on cloud physics.
Note also that the equilibrium line for ice and vapor lies below the equilibrium line for supercooled liquid and vapor for every temperature. Thus esi < es for every temperature below 0 oC because ls > lv in the Clausius–Clapeyron Equation. This small difference between esi and es can be very important in clouds, as we will also see in the lesson on cloud physics.
Quiz 3-2: Humidity and relative humidity.
- Find Practice Quiz 3-2 in Canvas. You may complete this practice quiz as many times as you want. It is not graded, but it allows you to check your level of preparedness before taking the graded quiz.
- When you feel you are ready, take Quiz 3-2. You will be allowed to take this quiz only once. Good luck!