6.6 Which wavelength has the greatest spectral irradiance?
6.6 Which wavelength has the greatest spectral irradiance?
The peak of this distribution as a function of wavelength can be found by taking the derivative of Pe(λ) with respect to wavelength, setting the value equal to 0, and solving for the wavelength. The result is the Wien Displacement Law:
[6.5]
For the sun with a photospheric temperature of about 5780 K, λmax ~ 0.500 μm or 500 nm, which is the color green. However, for Earth with a mid-tropospheric temperature of about 260 K, the peak wavelength is closer to 11 μm, well into the infrared (see below).
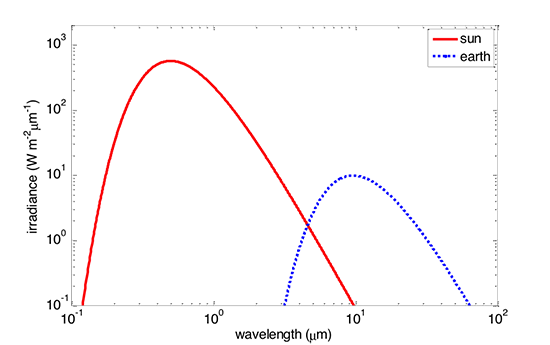
The spectral irradiance of solar radiation for a surface located at the top of Earth's atmosphere (red solid curve) and the spectral irradiance emitted by Earth into the upward hemisphere above its surface (blue dashed curve) To get these curves, we assumed that the Sun and the Earth both emit radiation according to the Planck distribution function spectral irradiance, which they do not quite do.
Credit: W. Brune