Lesson 8: Math and Conceptual Preparation for Understanding Atmospheric Motion
Overview
Overview
In previous lessons, we were able to explain physical and chemical processes using only algebra and differential and integral calculus. Thermodynamics, moist processes, cloud physics, atmospheric composition, and atmospheric radiation and its applications can all be quantified (at this level of detail) with fairly simple mathematics. However, more math skill is required to understand and quantify the dynamics of the atmosphere.
This lesson introduces you to the math and mathematical concepts that will be required to understand and quantify atmospheric kinematics, which is the description of atmospheric motion; and atmospheric dynamics, which is an accounting of the forces causing the atmospheric motions that lead to weather. Weather is really just the wind (the motion of air in the horizontal and the vertical) and the consequences of the wind. Wind, which has both direction and speed, is best described using vectors.
The Earth is a spinning, slightly squashed sphere. The atmosphere is a tenuous thin layer on this orb, so from a human’s limited view, the Earth appears to be flat. For some applications, a simple Cartesian coordinate system, with three dimensions in the x, y, and z directions, seems like a good way to mathematically describe motion. For processes that occur on the larger scale, where the Earth’s curvature is noticeable, we must resort to using coordinates that are natural for a sphere.
The way wind direction is described sprang out of wind observations, and is now firmly implanted in the psyche of every weather enthusiast: easterly, northerly, westerly, and southerly. This wind convention, however, is quite different than that used in the equations that govern atmospheric motion, which are the basis of weather forecast models. Here we will see that a conversion between the two conventions is straightforward but requires some care.
Finally, we will see that movement of air can either be described by an observer at a fixed location (called the Eulerian framework) or by someone riding along with a moving parcel of air (called the Lagrangian framework). These two points-of-view are very different, but we will see that they are related to each other by advection, which is just the movement of air with different properties (such as temperature, pressure, and humidity) from a place upwind.
With this math and these concepts you will be ready to take on atmospheric kinematics and dynamics.
Learning Objectives
By the end of this lesson, you should be able to:
- calculate partial derivatives
- implement vector notation, the dot product, the cross product, and the del operator
- explain the different coordinate systems and how they are used
- convert between math and meteorological wind directions
- calculate temperature advection at any point on a map of isotherms (lines of constant temperature) and wind vectors
Questions?
If you have any questions, please post them to the Course Questions discussion forum. I will check that discussion forum daily to respond. While you are there, feel free to post your own responses if you, too, are able to help out a classmate.
8.1 This is why partial derivatives are so easy...
8.1 This is why partial derivatives are so easy...
Extra Credit Reminder!
Here is another chance to earn one point of extra credit: Picture of the Week!
- You take a picture of some atmospheric phenomenon—a cloud, wind-blown dust, precipitation, haze, winds blowing different directions—anything that strikes you as interesting.
- Add a short description of the processes that you think are causing your observation. A Word file is a good format for submission.
- Use your name as the name of the file. Upload it to the Picture of the Week Dropbox in this week's lesson module. To be eligible for the week, your picture must be submitted by 23:59 UT on Sunday of each week.
- I will be the sole judge of the weekly winners. A student can win up to three times.
- There will be a Picture of the Week dropbox each week through Lesson 11. Keep submitting entries!
In your first calculus class you learned about derivatives. Suppose we have a function f that is a function of x, which we can write as f(x). How does f change with a very small change in x? This change is quantified by the derivative of f with respect to x.
What about a new function that depends on two variables, h(x,y)? This function could, for example, give the height h of mountainous terrain for each horizontal point (x,y). So what is the derivative of h with respect to x? One way we determine this derivative is to fix the value of y = y1, which is the same as assuming that y is a constant and then taking the ordinary derivative of h with respect to x. Suppose we take a slice through the mountain in the x-direction at a fixed value of y = y1, that is, y kept constant. How does h vary with a small change in x on this slice? This change is quantified as
This is called the partial derivative of h with respect to x. It’s pretty easy to determine because we do not need to worry about how y might depend on x.
Similarly, we can find the partial derivative of h with respect to y. In this case, we assume that x is constant and then take the ordinary derivative of h with respect to y. This change is quantified as
Are the partial derivatives of h with respect to x and to y the same? Try different functions for h(x,y) to see if you can find one for which they are equal for all values of x and y. (hint: Try h(x,y) = a constant.) Can you find any others?
Check Your Understanding
Let . What is the partial derivative of h with respect to x?
We can also find the partial derivative of h with respect to y. Can you do this?
So you can see that the may be different for each value of y and may be different for each value of x. Thus, even if you are not entirely familiar with partial derivatives and their notation, you can see that they are no different from ordinary derivatives but you take the derivative with respect to just one variable at a time.
Need more practice?
(7:29)
Hey everyone! Welcome back! Today we're going to be doing some Partial Derivative problems. The first one that we're going to do is f of (x, y, z) equals x squared times y cubed times z to the four, and all that partial derivatives means is that we're going to be taking the derivative for every single variable in the problem. So, since there are three variables, we're actually going to have to take the derivative three times, once for each variable, and its' going to be a separate equation four each one. So we'll go in order. The first one we'll look at is x and the notation for partial derivative looks like this. This weird squiggly thing f, the weird squiggly thing x, so f, you get from here, so this is, you know, h of (x, y, z) then this becomes an h and then x is the first variable we're going to... we're going to do. So, we'll go ahead and say... now, when we're taking and... and when... when we take the partial derivative here with x, we say that we're taking the partial derivative with respect to x, that's how people call it, then we'll take the partial derivative with respect to y then with respect to z. So, looking at x, the way that we take the partial derivative with respect to x while still having these other variables in the equation is we treat the other variables like they're constants. And, what I like to do, and you get... you'll get faster and faster at it in your head, but the way that I like to do that just to make it really obvious because sometimes it's hard to understand how to hold those constant especially when... when you're first starting out, I like to actually put a constant in there for those numbers and then simplify the equation and then take the partial derivative so I can see it. So... so, what I would do here, for example, we're talking about holding y and z constant, as if they we're a constant number like two or three, so let's go ahead and put two in for... for... for y and z here. If we did, we would have... we would have x squared times two cubed times two to the fourth, right, because we... we plugged in two for y and for z. Okay? So, since we're keeping this constant, this is how the equation would simplify. So if... if you... if you multiply this out, let's see, this would actually be x squared times eight and this would be times sixteen, so this would be eighty and forty eight, so this would be x squared times a hundred and twenty eight, right, if you simplify that. So, what would be if we... if we were taking the derivative of this normally, we would be looking at a hundred and twenty eight x squared. We would take the derivative of this and if we would multiply two times the coefficient which is a hundred and twenty eight so that would be, what? Two hundred and fifty six, so the derivative of this would be two hundred and fifty six x, right? So, what I'm hoping that you can see from this is that it's... its... it's exactly the same thing. We're going to hold these two things constant and they are going to be like a coefficient and... and this two hundred and fifty six stays. So, this is actually going to be an... Let's go ahead and write out the answer and then we'll compare them. You're going to multiply these two out in front here so it's going to be two x and then y cubed z to the four. That's going to be the answer for the partial derivative and I that you can see the relationship here. We multiplied the two on the x squared out in front just like we did here, we... we brought this two out in front, and we ended up with a single x just like we ended up with a single x here and we left y cubed and z to the fourth because they were absorbed into the coefficient here. They are like... because they're constants and they're multiplied together, they are part of the coefficient, they're like part of this two which is why... which is why they get left in... in this equation. Let's go ahead and do y so that we see in another example and hopefully we'll start to understand. So, when we... when we take the partial derivative with respect to y as you might expect, it's going to be a partial derivative of f with respect to y, just like we did for x here. So now, with y, we're going to actually be holding... Oh, I hope you guys can't hear that fire truck. So with... with y, we're going to be keeping x and z constant so they're going to be like the coefficient as well, you could plug in numbers for them and... and go through the same exercise. But, they're like the coefficient so they're going to stay exactly the same because they're... they're multiplied here with the y so we're not even going to touch them. Remember, we didn't touched y cubed, we didn't touch z to the fourth so x and z, this time, are going to stay as well. So, all we're really looking at is... is the y and we're going to... we're going to do the same thing we did with x, take the derivative of y. So we're going to get that three out in front and then y squared, right, three y squared is the derivative of y cubed. So we took the derivative and then the x squared and the z to the fourth are just going to stay. So, that's the derivative with respect to y. I left the space because when you take the... the partial derivative, you always like to keep the variables in alphabetical order. So, I could have written three y squared x squared z to the fourth but we like to always keep them x, y, z in order. So, we'll go ahead and... and do the same thing here for z. So it's going to be the partial derivative of f with respect to z and we will go ahead and leave x squared and y cubed. We're not touching them because they're like part of the coefficient, they stay. So we'll go ahead and say x squared y cubed and then we... we take the derivative of z here. So the derivative... Of course, we subtract one from the exponent, so four minus one is three and the four gets multiply out in front so it comes out here. So our answer with respect to z is actually four x squared y cubed z cubed. And, your final answer is... is a three part answer if you're asked to take the... the... the derivative of this function or the partial derivative. Because there are three variables, you need each one of these equations and you would want to write all three of these down on the homework or on your test because... because your answer is actually all three of these. So, there you have it.
8.2 What you don’t know about vectors may surprise you!
8.2 What you don’t know about vectors may surprise you!
Remember that a scalar has only a magnitude while a vector has both a magnitude and a direction. The following video (12:33) makes this difference clear.
Hi it's Mr. Andersen and right now I'm actually playing Angry Birds. Angry Birds is a video game where you get to launch Angry Birds at these pig type characters. I like it for two reasons. Number one it's addictive, but number two it deals with physics and a lot of my favorite games deal with physics. So let's go to level two. And so, what I'm going to talk about today are vectors and scalars, and vectors and scalars are ways that we measure quantities in physics. Angry Birds would be a really boring game if I just use scalars because if I just use scalars I would input the speed of the bird and then I would just let it go, and it'd be boring because I wouldn't be able to vary the direction. And so Angry Birds I can vary the direction and let me try to skip this off of... nice. I can try to skip it off and and kill enough of these pigs at once. Now I could play this for the whole 10 minutes but that would probably be a waste of time. So, what I want to do is talk about scalars and vector quantities. Scalar and vector quantities I wanted to start with them at the beginning of physics because sometimes we get two vectors and people get confused and don't understand where did they come from. So, we have quantities that we measure in science especially in physics and we give numbers and units to those, but they come in two different types and those are scalar and vector. To kind of talk about the difference between the two, a scalar quantity is going to be a quantity where we just measure the magnitude, and so an example of a scalar quantity could be speed. So when you measure the speed of something and I say how fast does your car go, you might say that my car goes 109 miles per hour. Or, if you're a physics teacher you might say that my bike goes, I don't know like nine point six meters per second, and so this is going to be speed and the reason it's a scalar quantity is it simply gives me a magnitude. How fast, how far, how big, how quick. All those things are scalar quantities. What's missing from a scalar quantity is direction, and so vector quantities are going to tell you the not only the magnitude, but they're also going to tell you what direction that magnitude is in. So, let me use a different color maybe. Example of a vector quantity would be velocity, and so in science it's really important that we make this distinction between speed and velocity. Speed is just how fast something is going, but velocity is also going to contain the direction. In other words I could say that my bike is going 9.08 m/s West. Or, I could say this pen is being thrown with initial velocity of two point eight meters per second up or in the positive. And so, once we add direction to a quantity now we have a vector. Now you might think to yourself that's kind of nitpicky. Why do we care what direction that were flowing in and I have a demonstration that will kind of show you the importance of that, but a good example would be acceleration. So what is acceleration? Acceleration is simply change in velocity over time and so acceleration is going to be the change in velocity over time. and so I could ask you a question like this. let's say a car is driving down a road and it's going 23 meters per second and it stays at 23 meters per second. Is it accelerating? And you would say no of course it's not. Let's say it goes around a corner and during that movement around the corner it stays at 23 miles per hour. Well what would happen to the scalar quantity of speed around the corner? It would still be 23 meters per second, and so if you're using scalar quantities we'd have to say that it's not accelerating, but since the velocity is a vector if you're going 23 miles an hour and you go around a corner are you accelerating. Yeah, because you're not changing the magnitude of your speed, but you're clearly changing the direction and so a change in velocity is going to be acceleration. And so you are accelerating when you go around a corner. And so that be an example of why in physics, I'm not trying to be nitpicky I'm just saying that you have to understand the difference between a scalar quantity and then which is just magnitude, and a vector which is magnitude and direction. There's a review at the end of this minute video, and so I'll have you go through a bunch of these and so we'll identify a number of them, but for now I want to give you a little demonstration. To show you the importance of a scalar and vector quantities. So what I have here is a one thousand gram weight or one kilogram weight. It's suspended from a scale and I don't know if you can read that on there but the scale measures the number of grams. And so, if this is a thousand grams and this measures the number of grams and it's scaled right it should say and it does about a thousand grams is, is the weight of this. Now a question I could ask you is this, let's say I bring another scale and so I'm going to attach another scale to it. And so if we had one mass that had a mass of a thousand grams, and now I have two scales that are bearing the weight of that and I lift them directly up, what should what should each of the scales read. And if you're thinking well it's a thousand gram so each one should read 500 grams let me try it. The right answer is, yeah. Each of the scales ray right at about five hundred grands and so that should make sense to you. In other words 500 + 500 is a thousand so we have the force down of the weight force of tension that's holding these in position, and so we should be good to go. The problem becomes when I start to change the angle and so what I'm going to do and I'm sure this will go off screen, is I'm going to start to to hold these at a different angle. and so what if they look right here and now find that it's a six hundred and so this one is at 600 as well. and so as I increase the angle like this will find that that will increase as well and so when I get it to an angle like this I have a thousand gram weight and it's being supported by two scales now that are reading a thousand. and it's going to vary as I come back to here and if you do any weight lifting you understand kind of how that works. So the question becomes how do we do math? The problem with this then is the the numbers don't add up. And so, if I've got a 500 gram way excuse me a thousand gram weight being supported by two scales it made sense that it was weighing five hundred each. But now we all the sudden have a thousand gram weight being supported by two scales that are reading thousand and so this doesn't make sense or the math doesn't make sense. And the reason why is that you're trying to solve the problem from a scalar perspective, and you'll never be able to get the right answer because it's going to change its going to change depending on the angle that we lift them at. So, to understand this in a a vector method, and we'll get way into detail so I just kind of wanted to touch on it for just a second. What we had was a weight so we'll say there's a weight like this and will say that's a thousand gram weight and then we have two scales and each of those scales are pulling at 500 grams. So, if you add the vectors up, so this is 1 vector and this is another vector, so each of these are 500 grams so I make them 500 in length. Then we balance out in other words you have the balancing of this weight with these two weights that are on top of it. Now if we go to the vector problem the vector problem again we had a thousand gram weights a thousand grams in the middle, and then we had a force in this direction of a thousand and a force in that direction of the thousand. So we had the force down of a thousand, but we had a force of a thousand in this direction and a force of a thousand in that direction. And so, if you start to look of it at it like a vector quantity imagine this that we've gotta weight right here but you have to have two people pulling on it and so it's like this tug-of-war where it's not just in one direction but it's actually in two. And so you can start to see how these forces are going to balance out, but only if we look at it from the vector perspective. Let me show you what that would actually look like. So if we put these tails up this would be that force down of a thousand grams. This would be the force of the weight, but we also had a force in this direction so I'm doing the same rule where I'm lining up my vector from the tail to the tip and the tail to the tip. And so that diagram that I had in the last slide I'm actually moving this one force and you can see that they all sum up to 0. and so the reason I like to start talking about vectors and scalars with this problem is that you can never solve the problem if you're going to go at it from a scalar perspective. and we're going to do some really cool problems let's say I'm sliding a box across the floor, but how often do you slide a box across the floor and actually pull it straight across like that? if you're like me you're pulling a sled or something you normally pulling it at an angle and once we start playing at an angle becomes a totally different for us and we can't solve problems in the scalar way we have to go and solve it from the vector perspective and so that's the importance of vectors. on now it's a huge thing. So there are lots of things that we can measure in physics and so what I'm going to try to do hopefully can get this right is go through and circle all the scalar quantities and then go back and circle all the vector quantities. And so if you're watching this video a good thing to do would be pause right now and then you go through in and circle the ones that you think are scalar and vector, and then we'll see if we match up the end. Scalar quantities remember is simply going to be magnitude. And so the question I always ask myself when I'm doing this is, ok does it have a direction? Length is simply the length of a side of something, so I would put that in the scalar perspective. This is kind of philosophical, does time have a direction? I would say no. Acceleration we already talked about that. That's changing in velocity. What about density, the density of something. That definitely is a scalar quantity. If I say the density of that is 12.8 grams per cubic centimeter North that doesn't make sense at all. What are some other scalar quantities? Temperature would be a scalar quantity. It's just how fast the molecules are moving, but it's not in one certain direction. Pressure would be another one that is scalar. It's not directional. It's not in one direction, the pressure is remember, pressure air pressure is the one that I always think of is going to be in all direction, so we wouldn't say that. Let's see, mass. The mass of something is going to be a scalar quantity as well so it it doesn't change. Now wait and we'll talk more about that later and would actually be a a vector quantity. let's see if I'm missing any. now I think this would be good so let's change color for a second. So, displacement is how far you move from a location and that's in a direction. So we call that a vector quantity acceleration I mentioned before. force is going to be a vector and will do these force diagrams which are really fun later in the year. Drag is something slowing you down, so if your car it's what's slowing you down in the opposite direction of your movement, so the direction is important. Momentum is a product of velocity in the mass of an object, and lift we get from like an airplane wing. That would be a vector quantity because it's in a direction. So these are all vector quantities, the ones that I circled in red, but there are way more that we're going to find out there. And scalar quantities remember it's simply just magnitude or how big it is. And so as we go through physics be thinking to yourself is this a scalar quantity or vector? And if it's vector, my problem is a little bit harder, but like Angry Birds it's more fun when you go the vector route. And so, I hope that's helpful and have a great day!
Typically the vectors used in meteorology and atmospheric science have two or three dimensions. Let’s think of two three-dimensional vectors of some variable (e.g., wind, force, momentum):
Sometimes we designate vectors with bold lettering, especially if the word processor does not allow for arrows in the text. When Equations [8.3] are written with vectors in bold, they are:
Yet another notation uses parentheses and commas, as in A = (Ax, Ay, Az). Be comfortable with all of these notations.
In the equations for vectors, Ax and Bx are the magnitudes of the two vectors in the x (east–west) direction, for which or i is the unit vector; Ay and By are the magnitudes of the two vectors in the y (north–south) direction, for which or j is the unit vector; and Az and Bz are the magnitudes of the two vectors in the z (up–down) direction, for which or k is the unit vector. Unit vectors are sometimes called direction vectors.
Sometimes we want to know the magnitude (length) of a vector. For example, we may want to know the wind speed but not the wind direction. The magnitude of , or A, is given by:
We often need to know how two vectors relate to each other in atmospheric kinematics and dynamics. The two most common vector operations that allow us to find relationships between vectors are the dot product (also called the scalar product or inner product) and the cross product (also called the vector product).
The dot product of two vectors A and B that have an angle between them is given by:
The dot product is simply the magnitude of one of the vectors, for example A, multiplied by the projection of the other vector, B, onto A, which is just . Thus, if A and B are parallel to each other, then their dot product is AB. If they are perpendicular to each other, then their dot product is 0. The dot product is a scalar and therefore has magnitude but no direction.
Also note that the unit vectors have the following properties:
Note that the dot product of the unit vector with a vector simply selects the magnitude of the vector's component in that direction () and that the dot product is commutative .
Equation [8.4] can be rearranged to yield an expression for in terms of the vector components and vector magnitudes:
The cross product of two vectors A and B that have an angle between them is given by:
The magnitude of the cross product is given by:
where is the angle between A and B, with increasing from A to B.
Note that the cross product is a vector. The direction of the cross product is at right angles to A and B, in the right hand sense. That is, use the right-hand rule (have your hand open, curl it from A to B, and A x B will be in the direction of your right thumb). The magnitude of the cross product can be visualized as the area of the parallelogram formed from the two vectors. The direction is perpendicular to the plane formed by vectors A and B. Thus, if A and B are parallel to each other, the magnitude of their cross product is 0. If A and B are perpendicular to each other, the magnitude of their cross product is AB.
The following video (2:06) reminds you about the right-hand rule for cross products.
We're going to do a couple more examples of finding vector cross product. Suppose that I give you these two vectors a and B, which both lie in the plane of, look its my hands, which both lie in the plane of the page. Ok, so there are a and B. You want to find the direction of a cross B. To find the magnitude you do a times B times the sine of the angle between them, but we just want to find the direction right now, and to do this we're going to use the right hand rule, but first we can use a little bit of logic. So, first of all logic says this, whatever the direction of a cross B is which let's call that c, a cross b the we'll call that c. It has to be perpendicular to both a and B or perpendicular to the plane of the page. Well there are only two directions that that could be, right. What that means is that c either must point straight out of the page or it must point straight into the page. And, to figure out which one of those two directions it is, what we're going to have to do is we're gonna have to put our fingers along a. So there are two ways to do that. You can either put your fingers along a this way, or you could put your fingers along a this way, and you have to do it in the way that will let you swing a down into b like it was a little hinge. So, if you try that notice if you do it this way, yeah it's the wrong way right. You'd have to swing all the way the long way around. If you want to just simply fold a into b the way to do that is to put your fingers this way then you can curl them down this way. Notice when you do that your thumb is pointing into the page, so therefore, the answer is that c is into the page... and actually I got marker on my wall. Actually, the way we represent that is that's represented into the page is represented by a little X with a circle around it. You're supposed to think of it like the tail feathers of an arrow that's pointing into the page.
It follows that the cross products of the unit vectors are given by:
Note finally that .
We sometimes need to take derivatives of vectors in all directions. For that we can use a special vector derivative called the Del operator, .
Del is a vector differential operator that tells us the change in a variable in all three directions. Suppose that we set out temperature sensors on a mountain so that we get the temperature, T, as a function of x, y, and z. Then T would give us the change of T in the x, y, and z directions.
The Del operator can be used like a vector in dot products and cross products but not in sums and differences. It does not commute with vectors and must be the partial derivative of some variable, either a scalar or a vector. For example, we can have the following with Del operator and a vector A:
Quiz 8-1: Partial derivatives and vector operations.
- Find Practice Quiz 8-1 in Canvas. You may complete this practice quiz as many times as you want. It is not graded, but it allows you to check your level of preparedness before taking the graded quiz.
- When you feel you are ready, take Quiz 8-1. You will be allowed to take this quiz only once. Good luck!
8.3 Describing weather requires coordinate systems.
8.3 Describing weather requires coordinate systems.
In meteorology and other atmospheric sciences, we mostly use the standard x, y, and z coordinate system, called the local Cartesian coordinate system, and the spherical coordinate system. Let’s review some of the main points of these two systems.
Local Cartesian Coordinate System
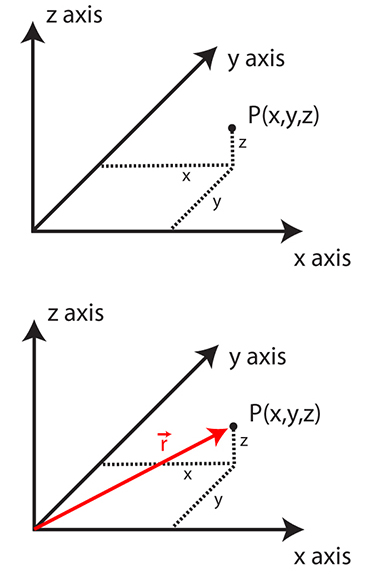
The local Cartesian coordinate system applies to three dimensions (as seen in the figure below). The convention is simple:
- The zero point, x = y = z = 0 or (0,0,0), is arbitrary.
- x increases to the east; x decreases to the west.
- y increases to the north; y decreases to the south.
- z increases going up; z decreases going down.
- A distance vector extending from the origin to (x,y,z) is given by r = i x + j y + k z.
Unit vectors (length 1 along standard coordinates) are i (east); j (north); k (up).
Often we will consider motion in two dimensions as being separate from motions in the vertical. We usually denote the horizontal with a subscript H; for example, rH = i x + j y, where rH is a horizontal distance vector.
This coordinate system works well over relatively small scales on Earth, perhaps the size of an individual state, where Earth's curvature is not important. This is why the qualifier "local" is used in the name of the coordinate system. This coordinate system does not work so well for large-scale motion on Earth, which is spherical.
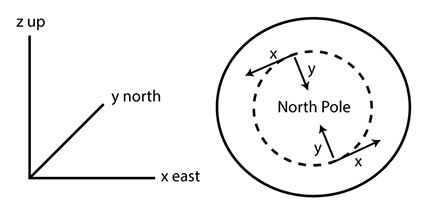
When we place the Cartesian coordinate system on a sphere, note that x always points toward the east, y always points toward the north, and z always points up along the direction of Earth’s radius (as seen in the figure above).
Spherical Coordinate System
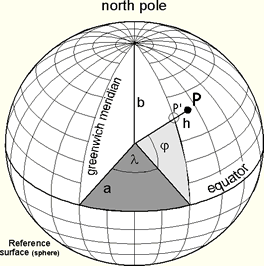
Life would be much easier if the Earth were flat. We could then use the local Cartesian coordinate system with no worries. But the Earth is very nearly a perfect sphere, which implies that to accurately describe motion, we must take the Earth’s spherical shape into account.
We use the following terms:
- r = distance from the center of the Earth
- = latitude (–90o to +90o, or – /2 to +/2)
- = longitude (–180o to 180o, or – to +)
- State College, PA is at .
Note that 1o of latitude is always 111 km or 60 nautical miles, but 1o of longitude is 111 km only at the equator. It is smaller in general and equal to 111 km x cos(). Note that 1 nautical mile = 1.15 miles.
To find the horizontal distance between any two points on Earth's surface, we first need to find the angle of the arc between them and then we can multiply this angle by Earth's radius to get the distance. To find the angle of the arc, , we can use the Spherical Law of Cosines:
where the latitude and longitude of the two points are , respectively and is the absolute difference between the longitudes of the two points. Note that the angle of the arc must be in radians, where . To find the distance, simply multiply this arc angle by the radius of the Earth, 6371 km.
Check Your Understanding
Show that 1o of latitude = 111 km distance.
Distance = 6371 km * (1/360)*2π = 111.2 km
In summary, we will use a local Cartesian coordinate system when our scales of interest are not too large (synoptic scale or smaller), but will need to use spherical coordinates when the scale of interest is larger than synoptic scale.
For another explanation of these two systems, visit this Coordinate Systems website [5].
Vertical Coordinates
Three different vertical coordinates are used in meteorology and atmospheric science: height, pressure, and potential temperature.
We have already introduced the vertical coordinate z, which is a height, usually in m or km, above the Earth's surface in the local Cartesian coordinate system; z is related to r in spherical coordinates through r = a + z, where a is the Earth's radius. The vertical coordinate z is the most commonly used in meteorology and in any process that involves getting off the ground, such as flight. Often pilots talk about flight levels, which are measured in hundreds of feet. So, flight level 330 is about 10 km altitude.
Another useful vertical coordinate is pressure, which decreases with height. Pressure is often a useful vertical coordinate in dynamics calculations. To a good approximation, pressure falls off exponentially with height, p = poexp(-z/H), as we learned in Lesson 2, so that ln(p) is fairly linear with height. We’ll get into this in greater detail later. For now, consider the following table of typically used pressure heights:
| altitude (km) | altitude (kft) | pressure level (hPa or mb) |
|---|---|---|
| 0 | 0 | 1000 |
| 1.5 | 4.9 | 850 |
| 3.0 | 9.8 | 700 |
| 5.5 | 18.0 | 500 |
A third important vertical coordinate is potential temperature, (Equation 2.58). This quantity is the temperature that an air parcel would have if it were brought to a pressure of 1000 hPa without any exchange of heat with its surroundings. This vertical coordinate has a nice property: air parcels tend to move on surfaces of constant potential temperature because moving on such a surface requires no energy. This coordinate is particularly useful in the stratosphere, where the rapid increase with altitude tends to keep air motion stratified.
8.4 Do you need a weathervane to see which way the wind blows?
8.4 Do you need a weathervane to see which way the wind blows?
Meteorologists use terms such as northeasterlies and southerlies when they describe winds. These terms designate directions that the winds come from. But when we think about the dynamic processes that cause the wind, we use the conventions for direction that are common in mathematics and in coordinate systems like the Cartesian coordinate system. The conversion between the two conventions—math and meteorology—is not simple. However, we will show you a simple way to do the conversion (see the second figure below).
Math Wind Convention
The wind vector is given by U = i u + j v + k w. The wind vector points to the direction the wind is going.
The subscript “H” will be used to denote horizontal vectors, such as the horizontal velocity, UH = i u + j v (though note that sometimes the symbols V , vH, and v will be used to denote the horizontal velocity). The magnitude of UH is UH = (u2 + v2)1/2. The math wind angle, , is the angle of the wind relative to the x-axis, so that tan() = v/u and the angle increases counterclockwise as the direction moves from the eastward x-axis ( = 0o) to the northward y-axis ( = 90o) .
Meteorology Wind Convention
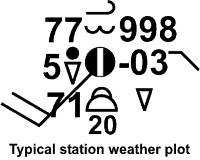
The meteorology wind convention is often used in meteorology, including station weather plots [7]. The wind vector points to the direction the wind is coming from. The angle is denoted by delta, , which has the following directions:
| direction wind is coming from | angle |
|---|---|
| north (northerlies or southward) | 0o |
| east (easterlies or westward) | 90o |
| south (southerlies or northward) | 180o |
| west (westerlies or eastward) | 270o |
Relationship Between Math and Meteorology Wind Conventions
Meteorology angles, designated by , increase clockwise from the north (y) axis. Math angles, designated by , increase counterclockwise from the east (x) axis.
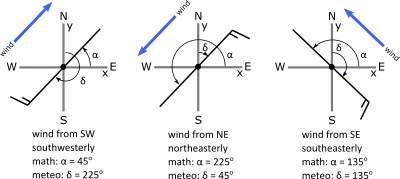
In the diagram on the left, the wind is southwesterly, the meteorology angle (measured clockwise from the north or y-axis) δ = 225o , and the math angle (measured counterclockwise from the east or x-axis) . If the wind is northerly (southward), the wind vane points to the north, the wind blows to the south, δ = 0o and α = 270o. If the wind is westerly (eastward), δ = 270o and α = 0o.
Note that in all cases, we can describe the relationship between the math and the meteorology angles as:
When the meteorology angle is greater than 270o, the math angle will be negative but correct. However, to make the math angle positive, simply add 360o.
Drawing a figure like those shown in the figure above often helps when you are trying to do the conversion. The following video (2:17) explains the conversion between meteorology and math wind angles using the figure above.
Meteorology description and wind direction originates from the compass and facing into the wind, where the wind comes from. The mathematical description of wind direction is based on the Cartesian xy grid and tracks the direction that the wind is going. We need to know both. Because the meteorology description, or medial angle, is used in the station weather plot. And we need the mathematical description, or math angle, for dynamics and a numerical weather prediction. Let's look at one example that relates the meteorology and math involves. First note that the grids are related, with positive x corresponding to east and positive y corresponding to north. Now let's add a wind, in this case a wind from the northeast, or northeasterly. From station weather plot the wind is from the northeast. Normally the wind bar would end in the center with a description of cloud cover. But we extend it past the center, toward the direction the wind is blowing, since that would be how we would draw the line and describe the wind direction in the mathematical xy coordinate system. The meteorology angle is measured clockwise from the north axis, just as it is for a compass-- 0, 90, 180, 270, 360, which is the same as 0. The math angle is measured counterclockwise from the x, or east, axis-- 0, 90, 180, 270, 360 or 0. It turns out that the math angle equals 270 degrees minus the meteorology angle. And also therefore the meteorology angle equals 270 degrees minus the math angle. So for this case that we've drawn here the meteorology angle equals 45 degrees. So the math angle equals 270 minus 45, which is 225 degrees. The meteorology angle is drawn clockwise. And the math angle as drawn counterclockwise. If the resulting angle is negative, simply add 360 degrees to make it positive.
Quiz 8-2: Finding coordinates and wind directions.
- Find Practice Quiz 8-2 in Canvas. You may complete this practice quiz as many times as you want. It is not graded, but it allows you to check your level of preparedness before taking the graded quiz.
- When you feel you are ready, take Quiz 8-2. You will be allowed to take this quiz only once. Good luck!
8.5 Gradients: How to Find Them
8.5 Gradients: How to Find Them
The gradient of a variable quantifies the magnitude and direction of the maximum change of the variable as a function of distance in space. For instance, the temperature gradient gives the maximum amount of temperature change in space and the direction of that maximum temperature change. Thus, a gradient is a vector.
We can find the gradient in Cartesian coordinates by using the del operator, which is also called the nabla or gradient operator, which is a vector that finds the partial derivative of a variable (please review 8.1) in each direction.
To see how we can calculate gradients, lets start with the commonly used gradient: the horizontal temperature gradient. Look at the surface temperature map for the United States on 8 September 2012.
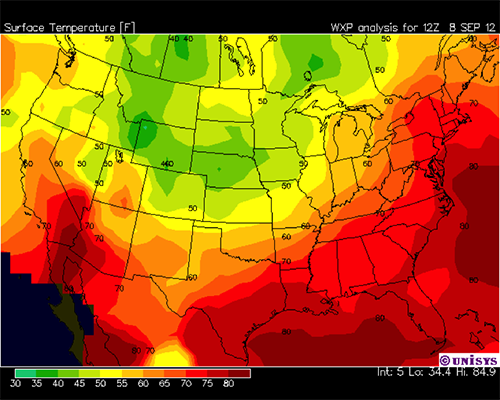
With the temperature data that was used to generate the map above, a computer can easily calculate the gradients for every location. However, you can get a better understanding of gradients by using a map, ruler, and the following mathemantical equations to estimate gradients. First, we show you how to find distances on a map using a ruler. Watch this video (2:12) on finding distances:
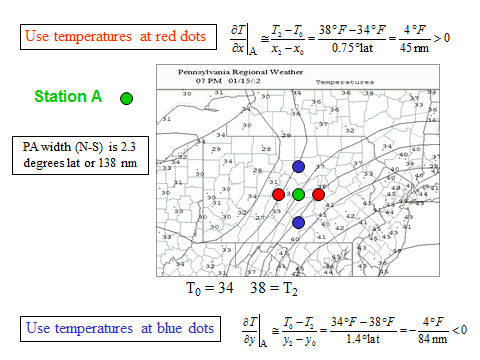
We're often interested in finding distances on a map so that we can calculate quantities we are interested in, such as the temperature gradient. Note first that often the projection of the map that we have does not have east-west, parallel, and straight across. In fact, the east-west line is curved a little bit, so take that into account when you're doing your calculations. Also note the north-south lines run a little bit not parallel as well. So how do we find distances? Well, there are many different ways, but one good way is to take a known distance on the map, scale it with a ruler, and then use that ruler in other places to give us distances in other places. So for instance, we know that the height of Pennsylvania between the two parallel borders, the north and south borders is 135 nautical miles. So we can scale that with a ruler, and I have a ruler here. I put the ruler in, and I see, in this particular case, the distance between the two is just about exactly 1 centimeter or 10 millimeters. So what that means is each millimeter on my scale is equal to 13.5 nautical miles on the map. So then I can use this in other places to measure other distances. So for instance, if I want to know the height of Kansas between its parallel North and South borders, I can put my ruler on there. And if I look carefully, I get a number that's about 13 and 1/2 millimeters. So 13 and 1/2 times 13 and 1/2 is about 182. And that's what I would say this distance is. The actual distance is 180 nautical miles, so in fact, the scaling I have is actually pretty good.
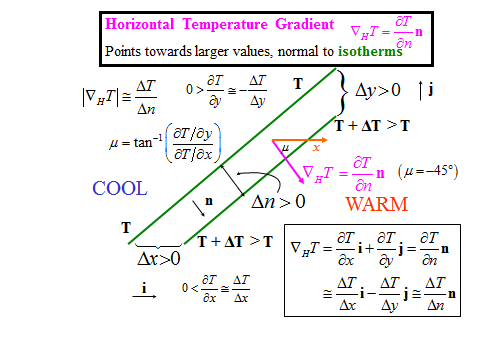
We can calculate a gradient for every point on the map, but to do this we need to know the change in the temperature over a distance that is centered on our chosen point. One approach is to calculate the gradients in the x and y directions independently and then determine the magnitude by:
and the direction by:
The partial derivatives are approximately equal to changes over small distances. Let's assume that the temperature gradient is approximately constant around a location. Then, integrating the equation 8.11, which is the definition of a horizontal gradient, yields
We can program a computer to do these calculations. However, often we just want to estimate the gradient. The gradient can be determined by looking at the contours on either side of the point and computing the change in temperature over the distance. These partial derivatives can be approximated by small finite changes in temperatures and distances, so that is replaced by in all places in these equations. We can calculate gradients by using “centered differences” as shown in the figures below.
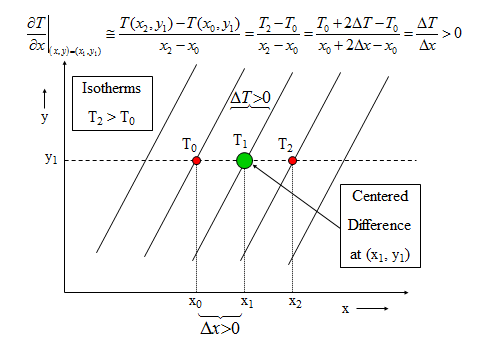
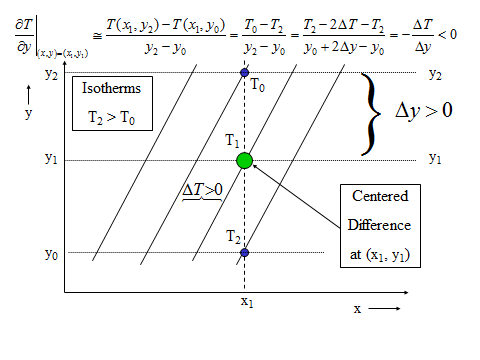
We then calculate the magnitude with Equation [8.12] and the direction with Equation [8.13], where we replace the partial derivatives with the small finite differences in all places in these equations.
The magnitude and direction are:
When you calculate the arctangent, keep in mind that the tangent function has the same values every 180o or every π radians. If you get an answer for the arctangent that is 45o, how do you know whether the angle is really 45o or 45o + 180o = 225o? The gradient vector always points towards higher values, so always choose the angle so that the gradient vector points toward the warmer air. Alternatively, if ∂T/∂x is greater than 0, choose the value of the arctangent between –90o and 90o, whereas if ∂T/∂x is less than 0, add 180o.
Recap of the process for calculating the temperature gradient:
- Determine the distance scale by any means that you can. Sometimes it is given to you; sometimes you can scale off a ruler; sometimes you just estimate it using the size of known boundaries.
- Determine the spacing between the isotherms.
- Find the temperature change in the x and y directions using the centered difference method. These two numbers, , are needed to calculate both the gradient magnitude and the gradient direction. Note that can be either positive or negative.
- Calculate the magnitude by finding the square root of the squares of the gradients in the x and y directions (i.e., ).
- Calculate the direction of the gradient vector by finding the arctangent of the y-gradient divided by the x-gradient. Pay attention to the direction—make sure that it points toward the warmer air.
Now watch this video (3:52) on finding gradients:
We can calculate the gradient by using the method that's described in the lesson. Let's pick a point in Pennsylvania about here, and then we'll calculate the gradient for that point. We will first look at the gradient in the x direction which goes along, and it's parallel with the North and South boundaries of Pennsylvania. We'll use the method of center differences that's described. We'll look at this contour here, this isotherm, and this one over here on the other side. And we note that this distance here is very, very similar to the distance of Pennsylvania between the parallel borders, which is 135 nautical miles. And so each one of these contours is four degrees Fahrenheit. So we have two of them, so 8 divided by 135 nautical miles gives us a gradient in the x direction of 0.059 degrees Fahrenheit per nautical miles. Now we can do the y direction, so we pick two points here. One here and one about here to be on the gradients. And we note that this is a little bit more than half the height of Pennsylvania. It's actually about 80 nautical miles. But also note that as y goes more positive, the temperature becomes more negative and therefore, we have to use minus 8 over 80. And we get, for the gradient in the y direction, minus 0.1 degrees Fahrenheit per nautical miles. When we put these in to get the magnitude-- it's the square root of the squares-- we see that we end up with 0.12 degrees Fahrenheit per nautical mile with a magnitude of the gradient. To find the direction of the gradient we see that mu, the angle with respect to the x-axis-- so this is a math angle. It's equal to the arctangent of the gradient in y divided by the gradient in x. And so that would be the arctangent of minus 0.1 over 0.059, which is minus 59 degrees. And that is, of course, measured from the x-axis here. So that is measured from this direction here like this, and so that's minus 59. And it's the same as if we went all the way around and we would get 301 for alpha if we were looking at the math angle. Now, we can look and get an idea about gradients and other places really quickly, so let's just take this point in Central Oregon. So now x is going like this over here, and so we see that the gradient in the East West direction, or x direction is-- to go to another country you have to go very, very far, and so that would be 8 degrees. It's so far the really the gradient is essentially 0. Whereas if we go in the North South direction-- that is in the y direction here-- we see that there's quite a substantial distance here. And so, since this is 8 degrees, just like this is 8 degrees over here, then what that means is the gradient is going to be quite a bit smaller in this direction than it is in Pennsylvania here where the isotherms are much, much closer together. So we would expect a gradient that's a fourth or a fifth of the gradient that we got for Pennsylvania, and so it'll be very weak. Nonetheless, it'll point toward the hotter air, and it'll look something like this.
A word about finding gradients in the real world. Sometimes the centered differences method is difficult to apply because the gradient is too much east–west or north–south. For instance, in the temperature map at the beginning of this section, the x-gradient is hard to determine by the centered difference method in the Oklahoma panhandle and the y-gradient is hard to determine in central Pennsylvania because in both cases, the temperature hardly changes in those directions. In these cases, you could say that the gradient in that direction equals 0, but then your computer program might have a hard time finding the arctangent. One way around this problem is to put in a very small number for the gradient in that direction, say 1 millionth of your typical gradient numbers, to do the calculation.
A second word about finding gradients in the real world. When you are finding temperature gradients from a temperature map, it is sometimes hard to determine the temperature gradient at some locations because the isotherms are not evenly spaced and can be curvy. Don't despair! Use your best judgment as to what the gradients are. Check your answers for the magnitude and direction of the temperature gradient vector by estimating the magnitude and direction by eyeballing the normal to the isotherms at that location and pointing the gradient vector to the warmer air. If your calculated direction is very different from your eyeballed value by more than, say, 45o, check your math.
Quiz 8-3: Grading your gradients.
- Find Practice Quiz 8-3. You may complete this practice quiz as many times as you want. It is not graded, but it allows you to check your level of preparedness before taking the graded quiz.
- When you feel you are ready, take Quiz 8-3. You will be allowed to take this quiz only once. Good luck!
8.6 What You Experience Depends on Your Point of View: Eulerian vs. Lagrangian
8.6 What You Experience Depends on Your Point of View: Eulerian vs. Lagrangian

Suppose you were driving underneath an eastward-moving thunderstorm at the same speed and in the same direction as the storm, so that you stayed under it for a few hours. From your point-of-view, it was raining the entire time you were driving. But from the point-of-view of people in the houses you passed, the thunderstorm approached, it rained really hard for twenty minutes, and then stopped raining.
If the people in houses formed a network of observers, and if they talked to each other, they would find that the thunderstorm moved rapidly from west to east in a path that rained on some houses and missed others. This point-of-view is called the Eulerian description because observers are at fixed locations and see the storm only when it is over them. You, on the other hand, followed along with the thunderstorm; any changes you saw were due to changes in the thunderstorm’s intensity only. Your point-of-view was a Lagrangian description because you stayed with the storm.
We can now generalize these ideas to any parcel of air, not just a thunderstorm. An air parcel is a blob of air that hangs more-or-less together as it moves through the atmosphere, meaning that its mass and composition are conserved (i.e., not changing) as it moves. It has a fairly uniform composition, temperature, and pressure, and has a defined velocity. An air parcel needs be large enough so that thermodynamic properties such as temperature, pressure and dewpoint temperature are well defined, but small enough so that it responds quickly to thermodynamic changes induced by air motions. Air parcel change shape as they move in air and bump into other air parcels. Even though air parcels do not live forever, they are very useful concepts in explaining the differences between the Eulerian and Lagrangian frameworks.
To Summarize
Eulerian Framework:
- Observes atmospheric properties and their changes at fixed locations
- Observes different air parcels as they pass by a location
- Tracks motion only if observers in many locations form a network and communicate their information
- Is the way most weather observations are taken and the way the most weather prediction models do computations
Lagrangian Framework:
- Observes atmospheric properties and their changes following a moving air parcel
- Tracks changes within the air parcel as it moves
- Being in the same air parcel makes it easier to test and to understand the basic physical principals causing changes in air parcel properties.
- Is a conceptual or numerical approach and is difficult to realize with observations
Here's an interesting fact. Radiosonde measurements are considered Eulerian for continental or global networks that span thousands of kilometers because they measure properties like temperature and humidity at most a few 10's of kilometers from their launch site. However, radiosonde measurements are actually neither Eulerian nor Lagrangian because a radiosonde moves in air but does not follow the same air parcel. A cup anemometer or sonic anemometer mounted on a stationary tower is an example of a Eulerian method of measuring wind velocity.
Discussion Forum 5: Eulerian and Lagrangian Points-of-View From Your Everyday Life
In the lesson, I presented an example of a driver in a car that happened to be traveling at the same speed as a rainstorm so that to the driver it was raining the entire time, while to the observers in the houses that the driver passed, the rain showers were brief. We could have given a second case in which there was widespread rain so that both the car driver and the house occupants observed constant rainfall for several hours. In the first case, the advection exactly matched the local rainfall change wherever the driver was, so that the driver was in rain constantly, but the house occupants saw rain only for a short while. In the second case, there was no gradient in the rainfall rate, so even if the storm was moving, neither the driver nor the house occupants observed a change in rainfall.
Think of one event or phenomenon from the Eulerian and Lagrangian points-of-view, one in which the event or phenomenon looks very different from the two points-of-view. These events do not have to be weather related. Be creative.
- You can access the Eulerian and Lagrangian Points-of-View Discussion Forum in Canvas.
- Post a response that answers the question above in a thoughtful manner that draws upon course material and outside sources.
- Keep the conversation going! Comment on at least one other person's post. Your comment should include follow-up questions and/or analysis that might offer further evidence or reveal flaws.
This discussion will be worth 3 discussion points. I will use the following rubric to grade your participation:
| Evaluation | Explanation | Available Points |
|---|---|---|
| Not Completed | Student did not complete the assignment by the due date. | 0 |
| Student completed the activity with adequate thoroughness. | Student answers the discussion question in a thoughtful manner, including some integration of course material. | 1 |
| Student completed the activity with additional attention to defending their position. | Student thoroughly answers the discussion question and backs up reasoning with references to course content as well as outside sources. | 2 |
| Student completed a well-defended presentation of their position, and provided thoughtful analysis of at least one other student’s post. | In addition to a well-crafted and defended post, the student has also engaged in thoughtful analysis/commentary on at least one other student’s post as well. | 3 |
8.7 Can the Eulerian and Lagrangian frameworks be connected?
8.7 Can the Eulerian and Lagrangian frameworks be connected?
Changes over time in properties, such as temperature and precipitation, can be expressed in Lagrangian and Eulerian frameworks, and often the changes are different in the two frameworks (as in the precipitation change for the thunderstorm example). We can express these changes mathematically with time derivatives. Suppose we have a scalar, R, which could be anything, but let’s make it the rainfall rate. It is a function of space and time:
To find the change in the rainfall rate R in an air parcel over space and time, we can take its differential, which is an infinitesimally small change in R:
where dt is an infinitesimally small change in time and dx, dy, and dz are infinitesimally small changes in x, y, and z coordinates, respectively, of the parcel.
If we divide Equation [8.15] by dt, this equation becomes:
where dx/dt, dy/dt, and dz/dt describe the velocity of the air parcel in the x, y, and z directions, respectively.
Let’s consider two possibilities:
Case 1: The air parcel is not moving. Then the change in x, y and z are all zero and:
So, the change in the rainfall rate depends only on time. is called the Eulerian or local time derivative, also called the local derivative. It is the time derivative that each of our weather observing stations record.
Case 2: The air parcel is moving. Then the changes in its position occur over time, and it moves with a velocity, , where:
A special symbol is given for the derivative when you follow the air parcel around. It is called the substantial derivative, also called the Lagrangian derivative, material derivative, or total derivative and is denoted by:
Mathematically, we can express this equation in a more general way by thinking about the dot product of a vector with the gradient of a scalar as we did in an example of the del operator:
where the second term on the right hand side is called the advective derivative, which describes changes in rainfall that are solely due to the motion of the air parcel through a spatially variable rainfall distribution.You should be able to show that equation [8.19] is the same as equation [8.18].
We can rearrange this equation to put the local derivative on the left.
The term on the left is the local time derivative, which is the change in the variable R at a fixed observing station. The first term on the right is the total derivative, which is the change that is occurring in the air parcel as it moves. The last term on the right, , is called the advection of R. Note that advection is simply the negative of the advective derivative.
To go back to the analogy of the thunderstorm, the change in rainfall that you observed driving in your car was the total time derivative and it depended only on the change in the intensity of the rain in the thunderstorm. However, for each observer in a house, the change in rainfall rate depended not only whether the rainfall within the thunderstorm was changing with time (which would depend, for example, on the stage of the storm) but also on the movement of the thunderstorm across the landscape.
R can be any scalar. Rainfall rate is one example, but the most commonly used are pressure and temperature.
Equation [8.20] is called Euler’s relation and it relates the Eulerian framework to the Lagrangian framework. The two frameworks are related by this new concept called advection.
Let’s look at advection in more detail, focusing on temperature.
We generally think of advection being in the horizontal. So often we only consider the changes in the x and y directions and ignore the changes in the z direction:
So what’s with the minus sign? Let’s see what makes physical sense. Suppose T increases only in the x-direction so that:
If u > 0 (westerlies, blowing eastward), then both u and are positive so that temperature advection is negative. What does this mean? It means that colder air blowing from the west is replacing the warmer air, and the temperature at our location is decreasing from this advected air. Thus should be negative since time is increasing and temperature is decreasing due to advection.
If the temperature advection is negative, then it is called cold-air advection, or simply cold advection. If the temperature advection is positive, then it is called warm-air advection, or simply warm advection.
Some examples of simple cases of advection show these concepts (see figure below). When the wind blows along the isotherms, the temperature advection is zero (Case A). When the wind blows from the direction of a lower temperature to a higher temperature (Case B), we have cold-air advection. When the wind blows as some non-normal direction to the isotherms, then we need to multiply the magnitude of the wind and the temperature gradient by the cosine of the angle between them. We can estimate the temperature advection by doing what we did for the gradient, that is, replace all derivatives and partial derivatives with finite .

When the isotherms with the same temperature difference are further apart on the map (see figure below), then the horizontal temperature advection will be less than when the isotherms are closer together, if the wind velocity is the same in the two cases.
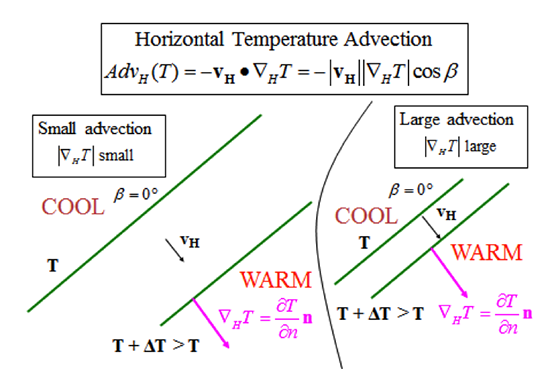
In summary, to calculate the temperature advection, first determine the magnitude and the direction of the temperature gradient. Second, determine the magnitude and direction of the wind. The advection is simply the negative of the dot product of the velocity and the temperature gradient.
Watch this video (2:20) on calculating advection:
Temperature advection is just a dot product of the velocity vector and the temperature gradient vector at that point. Let's choose this point in Pennsylvania where we've already calculated the gradient of this point. Let's look at the wind vector. So the station weather plot has a wind barb that's northwesterly and five knots. And so we can estimate, since this is x direction, and since this is north, we can estimate that this is about 300 degrees in terms of meteorology angle. So to find the math angle, which is what we need for the calculation here, we need to take 270 degrees. And we subtract 300 degrees from that, and we get alpha equals minus 30, which is 330 degrees if we start from the x-axis and we go counterclockwise all the way around to this direction like this. We've already figured out that the gradient has an angle that's 301 degrees, and that's from the x-axis going all the way around. So that's something like this. And therefore, the difference between the two is 29 degrees. And that's beta. We know that the magnitude of the temperature gradient is 0.12 degrees Fahrenheit. So we multiply the magnitude of the velocity times the magnitude of the temperature gradient times cosine of 29 degrees. We end up getting a value of 0.52 and the minus sign degrees Fahrenheit per hour. So the minus sign is here, because this is positive, positive, and positive. And so the advection is minus 0.52 degrees Fahrenheit per hour. This is cold air advection, or cold advection.
Quiz 8-4: The advection connection.
- Find Practice Quiz 8-4 in Canvas. You may complete this practice quiz as many times as you want. It is not graded, but it allows you to check your level of preparedness before taking the graded quiz.
- When you feel you are ready, take Quiz 8-4. You will be allowed to take this quiz only once. Good luck!
Summary and Final Tasks
Summary and Final Tasks
You now have all of the math tools that you will need to understand the lessons on kinematics and dynamics. For some of you, the concept of partial derivatives is new, but you see how easy it is to apply. We have reviewed vectors and a little vector calculus that you will need in the next few lessons. Dot products and cross products will appear frequently in the next few lessons, so make sure that you are comfortable with them and their applications. We introduced a new operator, the “del” or “gradient” operator, which is essential for describing weather observations and how atmospheric properties vary in space. There are two major coordinate systems that are used to describe atmospheric motion: local Cartesian and spherical. And there are three different coordinates that are used to define the vertical distance starting at Earth’s surface and rising radially: height z (m); pressure or logarithm of pressure p (hPa); and potential temperature (K). You will become skilled in converting between the meteorological wind directions shown on weather maps and in station weather plots and the wind direction needed to do calculations of wind motion and its effects. We introduced the concepts of the Eulerian and Lagrangian frameworks and showed that they are related by advection of a scalar, which is simply the dot product of the wind velocity and the gradient of the scalar.
Once you successfully complete the activities in this lesson, you will be ready to learn about atmospheric kinematics (the description of air movement) and atmospheric dynamics (the study of why air moves the way that it does).
Reminder - Complete all of the Lesson 8 tasks!
You have reached the end of Lesson 8! Double-check that you have completed all of the activities before you begin Lesson 9.