9.2 Watch these air parcels move and change.
9.2 Watch these air parcels move and change.
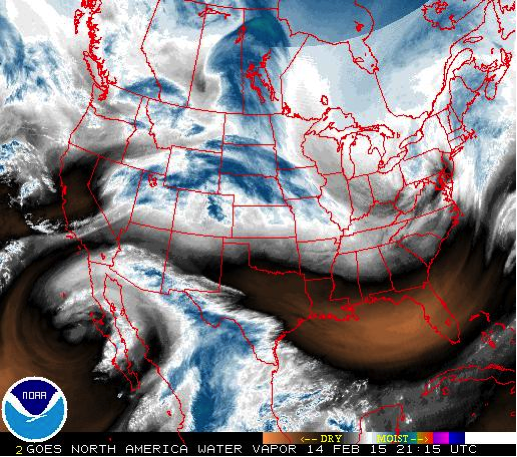
The water vapor image from the GOES 13 satellite, above, indicates different air masses over the United States. As we know from Lesson 7, the water vapor image actually shows the top of a column of water vapor that strongly absorbs in the water vapor channel wavelengths, but it is not a bad assumption to think that there is a solid column of moister air underneath the water vapor layer that is emitting and is observed by the satellite. In a single snapshot, it is not possible to see what happens to the air parcels over time. But if we look at a loop, then we can see the air parcels moving and changing shape as they move.
Watch a Loop
Watch the loop in the animated image below to see. Pick any air parcel with more water vapor in the first frame and then watch it evolve over time. What does it do? Maybe it moves; it spins; it stretches; it shears; it grows. Maybe it does only a few of these things; maybe it does them all.
We can break each air parcel’s complex behavior down into a few basic types of flows and then mathematically describe them. We will just describe these basic motions here and show how they lead to weather.

Assume that we have an air parcel as in the figure above. We focus on motion in the two horizontal directions to aid in the visualization (and because most motion in the atmosphere is horizontal) but the concepts apply to the vertical direction as well. If the air parcel is moving and does not change its orientation, shape, or size, then it is only undergoing translation (see figure below).
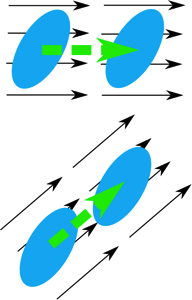
The air parcel can do more than just translate. It can undergo changes relative to translation, and its total motion will then be a combination of translation and relative motion. Let’s suppose that different parts of the air parcel have slightly different velocities. This situation is depicted in the figure below.
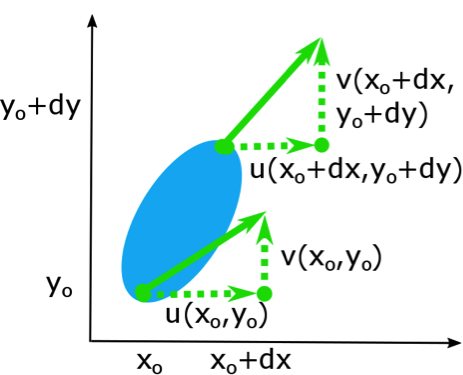
If we consider very small differences dx and dy, then we can write u and v at point (xo + dx,yo + dy) as a Taylor series expansion in two dimensions:
We see that u(xo,yo) and v(xo,yo) are the translation, and the relative motion is expressed as gradients of u in the x and y directions and gradients of v in the x and y directions.
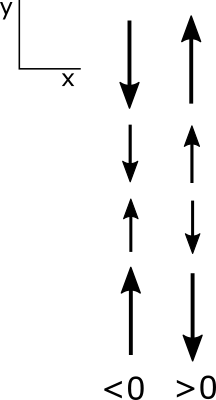
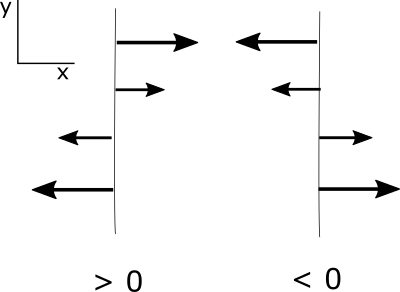
There are four gradients represented by the four partial derivatives. Each can be either positive or negative for each partial derivative.
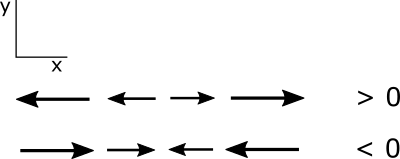
is the following change in velocity in the x direction:
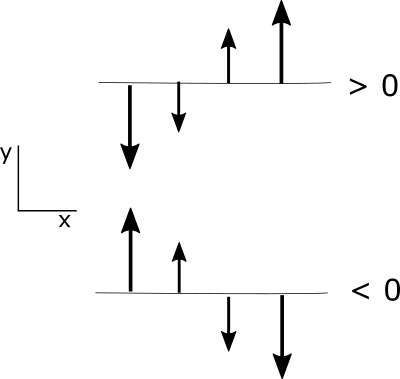
Note that a partial derivative is positive if a positive value is becoming more positive or a negative value is becoming less negative. Similarly, a negative partial derivative occurs when a positive value is becoming less positive or a negative value is becoming more negative. Be sure that you have this figured out before you go on.
Watch this video (2:38) for further explanation:
I want to make sure that you understand the partial derivatives of the u and v velocity with respect to x and y because we will soon be using these terms a lot. Let's start with the partial derivative u with respect to x. Consider a constantly increasing x so that the change in x is positive. As x increases, u becomes initially less negative, hence a positive change; then becomes positive, another positive change; and then becomes more positive, another positive change. Since the change in u and the change in x are both always positive, the partial derivative is positive, greater than 0. Look at the case where a partial derivative is less than 0, or negative. As x increases, u becomes less positive hence, a negative change. Then becomes negative, another negative change, then becomes more negative, another negative change. Since the change in u is always negative with a positive change in x, the partial derivative is always negative. Same logic applies to the partial derivative of v with respect to y. Up is positive for y, so you should look at how v changes as y becomes more positive. Look at the case of the change in u with respect to y. It does not matter that u is in the x direction perpendicular to y because we are interested in how u changes as a function of y. Let's look at what happens as y becomes more positive. On the left, u becomes less negative, a positive change in u, then positive, and more positive. Thus the partial derivative is a positive change in u over a positive change in y and therefore is positive, or greater than 0. The change in u with respect to y is always positive in this case. Using the same logic on the right, we see that the change in u with respect to y is always negative. And because a change in y is positive, the partial derivative is negative, or less than 0. The same logic applies to the partial derivative of v with respect to x. To the right is positive for x. So you can determine how v changes as x becomes more positive to see whether the partial derivative is positive or negative.