The Components of the Climate System
The climate system reflects an interaction between a number of critical sub-systems or components. In this course, we will focus on the components most relative to modern climate change: the atmosphere, hydrosphere, cryosphere, and biosphere. Please watch the following video to walk through the important aspects of these components.
Video: The Components of the Climate System (1:52)
PRESENTER: This is a schematic of the climate system. We can think of the climate as representing essentially four subsystems that are coupled together.
Among those subsystems are the atmosphere-- so that's one of the spheres. And that, of course, represents the chemistry and the dynamics of that component of the system, the atmosphere.
Then we have the hydrosphere, which is all the water that exists on the face of the earth in liquid form. So that would be the oceans and seas, rivers, lakes, et cetera. Water that exists in vapor form-- water vapor-- is part of the atmosphere.
Then we have the cryosphere, which is all of the water that exists in the form of snow and ice. That would include mountain glaciers, that would include the major ice sheets, and that would include snow that falls in the extra tropics during the winter.
Finally, then we have the biosphere, and that represents all living things on the face of the earth. And as we'll see in this course, the biosphere does indeed play a key role. It influences the composition of the atmosphere through the global carbon cycle, it influences the surface characteristics of the land, which has implications for climate.
So ultimately what we have are these four systems-- the hydrosphere, the atmosphere, the cryosphere, and the biosphere-- interacting with each other to form what we call the climate system PRESENTER: I think that this course fits into the major, energy and sustainability of policy, in a very vital way. I mean, climate change, in a sense, is sort of the 800-pound gorilla when it comes to the future energy policy. We need to take into account the fact that there are impacts, and there will continue to be impacts, that will grow in magnitude if we continue on our course of deriving energy from fossil fuel burning.
Decision-making ultimately relies upon taking both costs and benefits into account, and with climate change, there are costs, and many of those costs lie in our future. And in order to make appropriate decisions about how we balance the benefits of the energy that we can get today relatively cheaply from burning fossil fuels with the cost to society and to our environment of our continued reliance on fossil fuel burning, to really take on that big question, we need to understand the basics of climate change.
What is it about? What's causing it? What are the impacts, and what are the likely costs of future climate change? And how do we take into account these costs and benefits in making actual decisions about our energy future? So, hopefully, by the time this course is done, we will have brought all of those things together in a way that students can now think about this problem in a way that they wouldn't have been able to before they took the course.
Atmospheric Structure and Composition
The atmosphere is, of course, a critical component of the climate system, and the one we will spend the most time talking about.
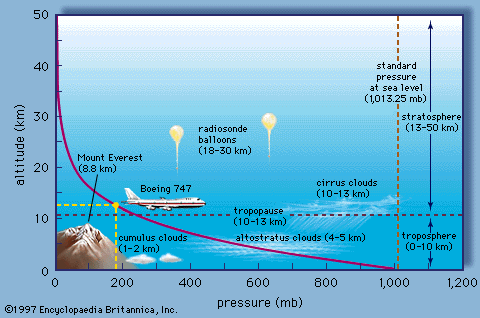
One key feature about the atmosphere is the fact that pressure and density decay exponentially with altitude:
As you can see, the pressure decays nearly to zero by the time we get to 50 km. For this reason, the Earth's atmosphere, as noted further in the discussion below, constitutes a very thin shell around the Earth.
The exponential decay of pressure with altitude follows from a combination of two very basic physical principles. The first physical principle is the ideal gas law. You are probably most familiar with the form , but that form applies to a bounded gas, where the volume can be defined. In our case, the gas is free, and the appropriate form of the ideal gas law is
where is the atmospheric pressure, is the density of the atmosphere, is the gas constant that is specific to Earth's atmosphere, and is temperature.
The 2nd principle is the force balance. There are two primary vertical forces acting on the atmosphere. The first is gravity, while the other is what is known as the pressure gradient force — it is the support of one part of the atmosphere acting on some other part of the atmosphere. This balance is known as the hydrostatic balance.
The relevant pressure gradient force in this case is the vertical pressure gradient force. When we are talking about a continuous fluid (which the atmosphere or ocean is), then the correct form of force balance involves force per unit volume of fluid.
In this form, we have for gravity (the negative sign indicates a downward force):
where is Earth's surface gravitational acceleration ( ).
The pressure gradient force has to be written in terms of a derivative:
The positive sign ensures that an atmosphere with a greater density below exerts a positive (upward) force.
In equilibrium, these forces must balance, i.e.
Now we can use the ideal gas law (eq. 1.) to substitute for ρ, the expression , giving
or re-arranging a bit,
The term in parentheses can be treated as a constant (in reality, temperature varies with altitude, but it varies less dramatically than pressure or density, so it's easiest to simply treat it as a constant).
This is a relatively simple first order differential equation.
Self Check...
Do you remember how to solve this first order differential equation from your previous math studies?
Click for answer.
Or, we can exponentiate both sides to yield:
The expression for atmospheric pressure as a function of altitude is:
where is the surface pressure, and is the surface height (by convention typically taken as zero).
This equation is known as the hypsometric equation.
The combination has units of inverse length, and so we can define a scale height (assuming a mean temperature ,
and write:
this gives an exponential decline of pressure with height, with the e-folding height equal to the scale height, representing the altitude at which pressure falls to roughly 1/3 of its surface value. At this altitude, which as you can see from the above graphic is just a bit below the height of Mt. Everest, roughly 2/3 of the atmosphere is below you.
Self-check...
Using the hypsometric equation (9 above), estimate the altitude at which roughly half of the atmosphere is below you.
Click for answer.
Take logs of both sides and rearrange:
Take and use from earlier:
Let us look at the vertical structure of the atmosphere in more detail, define some key layers of the atmosphere:
Video: Key Layers of the Atmosphere (2:41)
PRESENTER: We're going to-- OK. Well, let's talk a little bit about Earth's atmosphere. Here we're viewing Earth from outer space. And we can see there's this faint blue shell encasing the planet. And that faint blue shell is indeed Earth's atmosphere. So this gives us a sense of how relatively thin Earth's atmosphere actually is.
As it turns out, the lower 80 kilometers-- so that is, the first 80 kilometers above the Earth's surface-- contains just about 99% of the atmosphere. So the atmosphere really is this thin blue shell around the Earth.
Now, we can further decompose the atmosphere into various layers. The lowest of these layers is what we call the troposphere. Depending on the latitude, it's somewhere between the first 10 and 14 kilometers. And it's the area of the atmosphere within which we reside, in which most of Earth's surface resides-- in fact, all of Earth's surface, even the tallest mountains. It's also the layer within which weather takes place.
Now, this plot here shows temperature as a function of altitude. And we can see that, within the troposphere, temperatures decrease. It turns out they decrease at a rate of about 6 and 1/2 degrees Celsius per kilometer. And they continue to do so until we reach this boundary here between the troposphere and the next layer up, the stratosphere, where that temperature trend reverses and temperatures, in fact, start to increase as we go up further in the atmosphere. The boundary between these two layers is what we call the tropopause.
Now, why do temperatures increase as we get into the stratosphere? Well, it has to do with the chemistry of the atmosphere. And in fact, the existence of ozone within the stratosphere-- it's the photodissociation of ozone by solar radiation and the heat given off during that photodissociation process that actually heats the stratosphere and leads to the increasing temperatures as we go up in the atmosphere.
Now primarily, in this course, we are going to focus on the troposphere and to some extent the stratosphere. Those are the main parts of the atmosphere that we're going to be interested in.
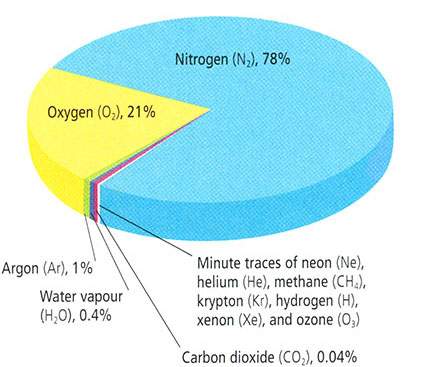
- Nitrogen (N2), 78%
- Oxygen (O2), 21%
- Argon (Ar), 1%
- Water vapor (H2O), 0.4%
- Carbon dioxide (CO2), 0.04%
- Minute traces of: neon (Ne), helium (He), methane (CH4), krypton (Kr), hydrogen (H), xenon (Xe), and ozone (O3)
© 2015 Pearson Education, Inc.
Now, let us talk a bit more about the atmospheric composition:
The atmosphere is mostly nitrogen and oxygen, with trace amounts of other gases. Most atmospheric constituents are well mixed, which is to say, these constituents vary in constant relative proportion, owing to the influence of mixing and turbulence in the atmosphere. The assumption of a well-mixed atmosphere and the assumption of ideal gas behavior, were both implicit in our earlier derivation of the exponential relationship of pressure with height in the atmosphere.
There are, of course, exceptions to these assumptions. As discussed earlier, ozone is primarily found in the lower stratosphere (though some is produced near the surface as consequence of photochemical smog). Some gases, such as methane, have strong sources and sinks and are therefore highly variable as a function of region and season.
Atmospheric water vapor is highly variable in its concentration, and, in fact, undergoes phase transitions between solid, liquid, and solid form during normal atmospheric processes (i.e., evaporation from the surface, and condensation in the form of precipitation as rainfall or snow). The existence of such phase transitions in the water vapor component of the atmosphere is an obvious violation of ideal gas behavior!
Of particular significance in considerations of atmospheric composition are the so-called greenhouse gases (CO2, water vapor, methane, and a number of other trace gases) because of their radiative properties and, specifically, their role in the so-called greenhouse effect. This topic is explored in greater detail later on in this lesson.