We will wrap up our discussion of climate change projections with a discussion of so-called tipping points. Tipping points are important because they represent possible threshold responses to forcing. While many of the climate change impacts we have looked at, like surface temperature increases, are projected to follow increasing atmospheric concentrations in a smooth manner, there are other responses that can be more abrupt—once a certain amount of warming takes place, some component of the climate system abruptly transitions to some other regime of behavior. We saw an example of this sort of behavior in our discussion in Lesson Five (see the series of videos at the bottom of this Lesson Five page) of the role of ice-albedo feedback in the long-term evolution of the Earth's climate system. In that case, we saw that there is the potential for more than one equilibrium state of the Earth's climate under a given state of the solar constant. When that is the case, it is possible that one or more of the steady states is unstable. In that case, a small perturbation can cause the system to spontaneously transition from its current state to a very different, other equilibrium state.
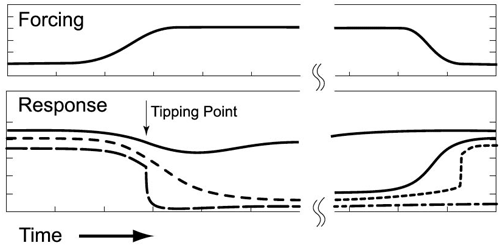
We have already seen some examples of potential climate tipping points—e.g., in the potential response of the cryosphere or patterns of ocean circulation to ongoing warming. There are many other potential tipping points in the system, however. These include the possibility that the ENSO phenomenon might transition rather suddenly into a very different mode of behavior, or that the Indian monsoon system—whose role is so critical to fresh water availability in large parts of South Asia—might suddenly collapse. Other possibilities include one of the possible carbon cycle feedbacks alluded to previously in this lesson; that a sudden release of previously frozen methane from thawing permafrost suddenly enters into the atmosphere. It is, of course, possible that other tipping points exist that we are not even aware of yet! Can you think of any possibilities yourself? If so—this would be another good topic to bring into this week's discussion.
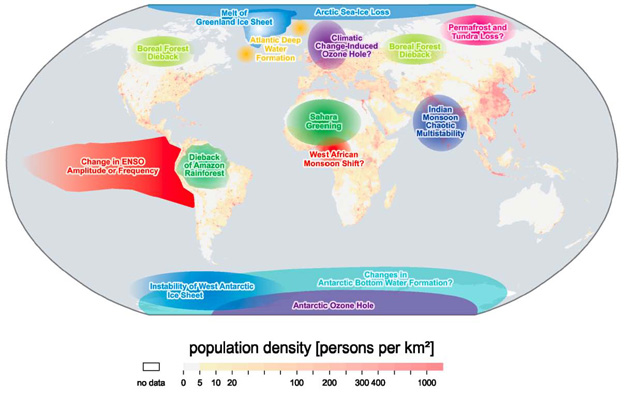
Tipping Points:
- Change in ENSO Amplitude or Frequency
- Boreal Forest Dieback
- Dieback of Amazon Rainforest
- Instability of West Antarctic Ice Sheet
- Melt of Greenland Ice Sheet
- Atlantic Deep Water Formation
- Antarctic Ozone Hole
- Changes in Antarctic Bottom Water Formation?
- Arctic Sea-Ice Loss
- Sahara Greening
- West African Monsson Shift?
- Climatic Change-Induced Ozone Hole?
- Permafrost and Tundra Loss?
- Indian Monsoon Chaotic Multistability
