Lesson 4 - Modeling of the Climate System, part 1
The links below provide an outline of the material for this lesson. Be sure to carefully read through the entire lesson before returning to Canvas to submit your assignments.
Introduction
About Lesson 4
We have now seen evidence indicating that the globe is warming, and that there is an array of other internally-consistent changes in the climate system that are associated with that warming. While these changes are suggestive of human-caused climate change, the existence of trends cannot alone be used to draw causal inferences.
That is where theoretical climate models come in. Climate models allow us to test particular hypotheses about climate change. For example, we can interrogate the models with respect to how much warming of the globe we might expect for a given change in greenhouse gas concentrations. In this lesson, we will consider the simpler classes of climate models, and we will engage in hands-on climate modeling activities.
What will we learn in Lesson 4?
By the end of Lesson 4, you should be able to:
- Describe the factors that govern Earth's climate system;
- Perform basic energy balance computations to estimate the surface temperature of the Earth;
- Perform basic energy balance computations to estimate the response of Earth's surface temperature to hypothetical changes in natural and anthropogenic forcing; and
- Explain what "equilibrium climate sensitivity" is.
What will be due for Lesson 4?
Please refer to the Syllabus for specific time frames and due dates.
The following is an overview of the required activities for Lesson 4. Detailed directions and submission instructions are located within this lesson.
- Problem Set #3: Estimate the warming due to an increase in CO2
- Read: Dire Predictions, v.2: p. 68-69
Questions?
If you have any questions, please post them to our Questions? discussion forum (not e-mail), located under the Home tab in Canvas. The instructor will check that discussion forum daily to respond. Also, please feel free to post your own responses if you can help with any of the posted questions.
Energy and Radiation Balance
We actually covered this topic back in the introductory lecture (lecture #1), so I'm going to ask you to simply review the Overview of the Climate System (part 2) [1] before continuing on to our initial discussion of climate models...
Simple Climate Models
We will start out our discussion of climate models with the simplest possible conceptual models for modeling Earth's climate. These models include different variants on the so-called Energy Balance Model. An Energy Balance Model or 'EBM' does not attempt to resolve the dynamics of the climate system, i.e., large-scale wind and atmospheric circulation systems, ocean currents, convective motions in the atmosphere and ocean, or any number of other basic features of the climate system. Instead, it simply focuses on the energetics and thermodynamics of the climate system.
We will start our discussion of EBMs with the so-called Zero Dimensional EBM—the simplest model that can be invoked to explain, for example, the average surface temperature of the Earth. In this very simple model, the Earth is treated as a mathematical point in space—that is to say, there is no explicit accounting for latitude, longitude, or altitude, hence we refer to such a model as 'zero dimensional'. In the zero-dimensional EBM, we solve only for the balance between incoming and outgoing sources of energy and radiation at the surface. We will then build up a little bit more complexity, taking into account the effect of the Earth's atmosphere—in particular, the impact of the atmospheric greenhouse effect—through use of the so-called "gray body" variant of the EBM.
Zero Dimensional EBM
The zero dimensional ('0d') EBM simply models the balance between incoming and outgoing radiation at the Earth's surface. As you'll recall from your review of radiation balance in the previous section, this balance is in reality quite complicated, and we have to make a number of simplifying assumptions if we are to obtain a simple conceptual model that encapsulates the key features.
For those who are looking for more technical background material, see this "Zero-dimensional Energy Balance Model" online primer [2] (NYU Math Department). We will treat the topic at a slightly less technical level than this, but we still have to do a bit of math and physics to be able to understand the underlying assumptions and appreciate this very important tool that is used in climate studies.
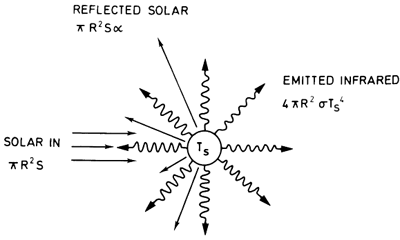
We will assume that the amount of shortwave radiation absorbed by the Earth is simply , where S is the Solar Constant (roughly 1370 W /m2 but potentially variable over time) and α is the average reflectivity of Earth's surface looking down from space, i.e., the 'planetary albedo', accounting for reflection by clouds and the atmosphere as well as reflective surface of Earth including ice (value of roughly 0.32 but also somewhat variable over time).
We will assume that the outgoing long wave radiation is given simply by treating the Earth as a 'black body' (this is a body that absorbs all radiation incident upon it). The Stefan-Boltzman law for black body radiation holds that an object emits radiation in proportion to the 4th power of its temperature, i.e., the flux of heat from the surface is given by
where σ is known as the Stefan-Boltzmann constant, and has the value ; ε is the emissivity of the object (unitless fraction) — a measure of how 'good' a black body the object is over the range of wavelengths in which it is emitting radiation; and Ts (K) is the surface temperature. For the relatively cold Earth, the radiation is primarily emitted in the infrared regime of the electromagnetic spectrum, and the emissivity is very close to one.
We will approximate the surface temperature, TS, as representing the average 'skin temperature' of an Earth covered with 70% ocean (furthermore, we will treat the ocean as a mixed layer of average 70m depth—this ignores the impacts of heat exchange with the deep ocean, but is not a bad first approximation). We can then approximate the thermodynamic effect of the mixed layer ocean in terms of an effective heat capacity of the Earth's (land+ocean) surface, . The condition of energy balance can then be described in terms of the thermodynamics, which states that any change in the internal energy per unit area per unit time (<) must balance the rate of net heating, which is the difference between the incoming shortwave and outgoing longwave radiation. Mathematically, that gives:
Let's suppose that the incoming radiation (the first term on the right hand side) were larger than the outgoing radiation (the second term on the right hand side). Then the entire right-hand side would be positive, which means that the left-hand side, the rate of change of Ts over time, must also be positive. In other words, Ts must be increasing. This, in turn, means that the outgoing radiation must increase, which will eventually bring the two terms on the right hand side into balance. At this point, there is no longer any change of Ts with time, i.e., we achieve an equilibrium.
In equilibrium, the time derivative term is, by definition, zero, and we thus must have equality between the outgoing and incoming radiation, i.e., between the two terms on the right-hand side of equation 1. This yields the purely algebraic expression
The factor of 1/4 comes from the fact (see Figure 4.1, below) that the Earth is emitting radiation over the entirety of its surface area (4πR2 where R is the radius of the earth), but at any given time only receiving incoming (solar) radiation over its cross-sectional area, πR2.
It turns out that since the Earth's surface temperature varies over a relatively small range (less than 30° K) about its mean long-term temperature (in the range of O° C, or 273° K), i.e., it varies only by at most 10% or so, it is valid to approximate the 4th degree term in equation (1) by a linear relationship, i.e.,
A and B, thus defined, have the approximate values: ;
Such an approximation is often used in atmospheric science and other areas of physics when appropriate, and is called linearization.
Using this approximation, we can readily solve for TS as
 [3]
[3]
You might find it rather disappointing that, after all the work we did above to develop a realistic Energy Balance Model for Earth's climate, we were way off. Our EBM indicates that, given appropriate parameter values (i.e., ), the Earth should be a frozen planet with TS = 255° K, rather than the far more hospitable TS= 288° K we actually observe. Our model gave a result that was a whopping 33° C (roughly 60° F) too cold!
Think About It!
What do you think we forgot?
Click for answer.
So, how do we include the effect of the atmospheric greenhouse effect in a simple way? That is the topic of our next section.
Simple Climate Models, cont'd
Gray Body Variant of the Zero Dimensional EBM
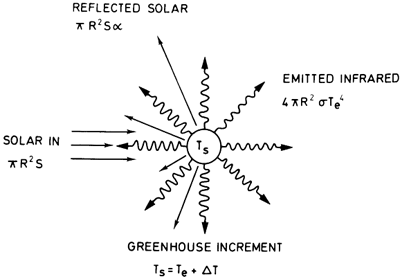
Even in the presence of the greenhouse effect, the net longwave radiation emitted out to space must balance the incoming absorbed solar radiation. So, we can think of the Earth system as still possessing an effective radiating temperature (Te), which is the black body temperature we calculated earlier with the zero-dimensional EBM and the black body parameter values for A and B, i.e., T = 255o K. It is the temperature Earth's surface has in the absence of any greenhouse effect. The outgoing longwave radiation to space is still given by . The atmosphere will have a temperature Te somewhere aloft in the cooler region of the mid-troposphere. If we like, we can think of the Earth as, on average, emitting temperature to space from this level; hence, we refer to the temperature as the effective radiating temperature.
When a greenhouse effect is present, the temperature at the surface, TS, will be substantially higher, however, due to the additional downward longwave radiation emitted by the atmosphere back down towards the Earth's surface.
We can attempt to account for this effect by simply changing the way we model the longwave radiation in the zero-dimensional EBM to account for the additional downward longwave radiation component.
Returning to the linearized form of the energy balance equation (i.e., equation (5) on the previous page), we will, therefore, now relax the assumption that A and B are given by their black body values. Instead, we will allow A and B to take on arbitrary values. This is a crude way of taking into account the fact that the Earth does not behave as a black body because the atmosphere has non-zero emissivity due to the presence of atmospheric greenhouse gases.
Simply put, we can tweak the values of A and B until they provide a good approximation. We refer to this generalized version of the black body approximation as the gray body approximation. The gray body model is a very crude way of accounting for the greenhouse effect in the context of a simple zero-dimensional model. In Lesson 5, we will build our way up to more realistic representations of the atmospheric greenhouse effect.
Various gray body parameter choices for A and B have been used by different researchers, in different situations. Since the gray body approximation is a linear approximation to a non-linear (Planck radiation) relationship, it is only valid over a limited range of temperatures about a given reference temperature. This means that a different set of parameters might be used for studying, e.g., the ice ages than would be used for studying, e.g., the early Cretaceous super greenhouse.
It turns out that the choices and yield realistic values for the current average temperature of the earth TS, and gives a value for the climate sensitivity — a concept we will define in the next section — that is consistent with mid-range IPCC estimates. We will, therefore, adopt these as our standard gray body parameter values, but we will also explore the impact of using alternative values a bit later.
Think About It!
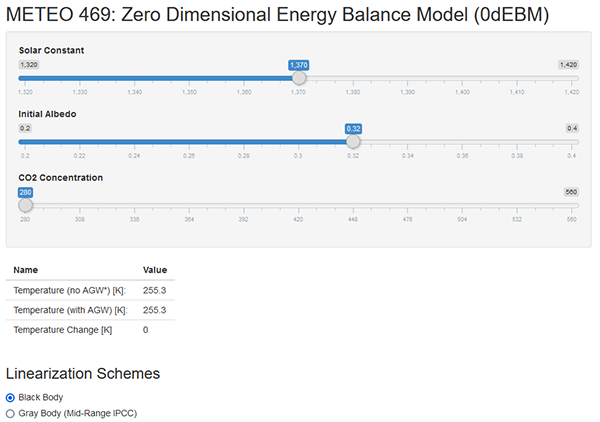
Use the Online 0d EBM Application [3] to estimate the average temperature of the Earth for the "mid-range IPCC" gray body parameter values. What surface temperature do you find, and how does it compare with the previous black body estimate of Earth's surface temperature?
Click for answer.
You should have found that TS = 288o K in the gray body approximation.
This is roughly 33o C (or 60o F!) warmer than the black body value.
In other words, the greenhouse effect has the effect of warming Earth from a frigid average temperature of -18o C to a far more hospitable 15o C!
The Concept of Equilibrium Climate Sensitivity
Let us rewrite the equation energy balance equation (5) on the previous page in a slightly different form,
where Fin represents the total incoming radiative energy flux at the surface, which includes incoming short wave radiation, but also any potential changes in the downward longwave radiation towards the surface.
Let us now consider the response of Ts to an incremental change in Fin. Since the 2nd term in (7) is a constant, we simply have
We can also rewrite (8) as
The change in downward longwave radiation forcing associated with a change in CO2 concentration from a reference concentration, [CO2]0 to some new value, [CO2], can be approximated by the following relationship from a paper by Myhre et al. (1998) [5]
Now, let us further specify that we are interested in the change in radiative forcing resulting from a doubling of atmospheric CO2 concentrations. For a CO2 doubling, e.g., an increase from pre-industrial levels of 280 ppm to twice that value, 560 ppm,
We can define equilibrium climate sensitivity, s, as the change in temperature resulting from a doubling of pre-industrial CO2 concentrations; s has units of K (or equivalently degrees C, since differences in C and K are equal). To estimate s, we combine equations (8) and (11)
The equilibrium climate sensitivity is the equilibrium warming we expect in response to CO2 doubling. In the simple case of the 0d EBM, it is readily calculated through equation (12).
Think About It!
Using the formula above (12), estimate the equilibrium climate sensitivity s for both the black body model and our standard version of the gray body model. Record your answers.
Click for answer.
For the black body model, we have:
, i.e., approximately 1K
For the standard gray body model, we have:
, i.e., approximately 3K.
Think About It!
Let's now use the Online 0d EBM Application [3] again to estimate the climate sensitivity for these two cases, by explicitly varying the CO2 level until you achieve a CO2 doubling, and recording the warming that you observed. Compare to the results you calculated above directly from the formula for climate sensitivity for the 0d EBM.
Click for answer.
We find the same answers that we found earlier, namely that the black body models gives just under 1o C warming, while the gray body model gives roughly 3o C warming.
As we will see later, this is close to the best current available estimate of the warming expected from a doubling of CO2 concentrations.
Problem Set #3
Activity
NOTE: For this assignment, you will need to record your work on a word processing document. Your work must be submitted in Word (.doc or .docx) or PDF (.pdf) format so I can open it.
The documents associated with this problem set, including a formatted answer sheet, can be found on CANVAS.
- Worksheet successfully downloaded! Be sure also to download the answer sheet from CANVAS (Files > Problem Sets > PS#3).
Each problem (#2 to #4) will be graded on a quality scale from 1 to 10 using the general rubric as a guideline. Problems #3 and #4 will each be worth twice as much as #2, meaning each of those two problems will be given a quality score as high as 10, which then will be multiplied by 2. Thus, a score (up to 10 points, 20 points, and 20 points from #2, #3, and #4, respectively) as high as 50 is possible, and that score will be recorded in the grade book.
The objective of this problem set is for you to work with some of the concepts and mathematics around zero-dimensional energy-balance models (0-D EBMs) covered in Lesson 4. You may find Excel useful in this problem set, but you may use any software you wish, keeping in mind that the instructor only can provide help with Excel.
- The following is the equation for planetary surface temperature under zero-dimensional energy balance, which is equation (5) on this page from Lesson 4 [6]:
Re-read the derivation of that equation in Lesson 4. After re-reading the derivation, explain what each variable in the equation is. Summarize also the assumptions behind the derivation; in other words, explain what a 0-D EBM is. This is as straightforward as it seems, but this problem is here to ensure that you understand the underlying concepts because they are referenced often in climate science. Report your discussion on the answer sheet.
- Report your responses to all parts of this problem on the answer sheet.
- Determine the planetary surface temperature TS for a blackbody Earth in both Kelvin and degrees Celsius, rounding to two decimal places. For the input values, let “A” be 315 W m-2 and “B” be 4.6 W m-2 °C-1 and the solar constant be 1,370 W m-2 and the planetary albedo value be 0.32, the “standard” values mentioned in Lesson 4. Although the answer to this question is given in Lesson 4, you MUST show explicitly all values substituted into the equation for TS. Be mindful of the order of operations as you perform the calculation.
- Recall that the graybody assumption is that Earth’s atmosphere has a greenhouse effect, i.e., the atmosphere itself emits longwave radiation downward to the surface. We account for it by varying the values of terms “A” and “B”. Let “A” be 214.4 W m-2 and “B” be 1.25 W m-2 °C-1 and the solar constant be 1,370 W m-2 and the planetary albedo value be 0.32. Calculate the planetary surface temperature for this conception of a graybody Earth, rounding the result to two decimal places and expressing it in both degrees Celsius and Kelvin. Once again, you MUST show explicitly all values substituted into the equation for TS.
- Using values of solar constant ranging from 0 to 2,000 W m-2, incremented by 100 W m-2, and assuming that the planetary albedo value is 0.32 and that term “A” is 214.4 W m-2 and “B” is 1.25 W m-2 °C-1, calculate planetary surface temperature, displaying the results in a table, expressing them in Kelvin, and rounding them to two decimal places. Also, plot the results, with the horizontal axis giving values of solar constant and the vertical axis giving values of planetary surface temperature.
- Using values of planetary albedo ranging from 0 to 1, incremented by 0.05 W m-2, and assuming that the solar constant is 1,370 W m-2 and that term “A” is 214.4 W m-2 and “B” is 1.25 W m-2 °C-1, calculate planetary surface temperature, displaying the results in a table, expressing them in Kelvin, and rounding them to two decimal places. Also, plot the results, with the horizontal axis giving values of planetary albedo and the vertical axis giving values of planetary surface temperature.
- Using values of term “A” ranging from 0 to 350 W m-2, incremented by 50 W m-2, and assuming that the solar constant is 1,370 W m-2, planetary albedo value is 0.32, and term “B” is 1.25 W m-2 °C-1, calculate planetary surface temperature, displaying the results in a table, expressing them in Kelvin, and rounding them to two decimal places. Also, plot the results, with the horizontal axis giving values of term “A” and the vertical axis giving values of planetary surface temperature.
- Using values of term “B” ranging from 0 to 5.0 W m-2 °C-1, incremented by 0.5 W m-2 °C-1, and assuming that the solar constant is 1,370 W m-2, planetary albedo value is 0.32, and term “A” is 214.4 W m-2, calculate planetary surface temperature, displaying the results in a table, expressing them in Kelvin, and rounding them to two decimal places. Also, plot the results, with the horizontal axis giving values of term “B” and the vertical axis giving values of planetary surface temperature.
- This problem will deal with the notion of climate sensitivity, which is described in Lesson 4 [7] Report all responses to the parts of this problem on the answer sheet.
- Write the equation that approximates the change in downward longwave radiation forcing associated with a change in CO2 concentration from a reference concentration to some new concentration value, defining each of the variables that are in the equation.
- Define equilibrium climate sensitivity in words, and write the equation that approximates it, defining each of the variables that are in the equation. How is this equation related to the equation that you wrote down in part (a)?
- The European Union has defined 2°C warming relative to pre-industrial temperatures as the threshold for Dangerous Anthropogenic Interference (DAI) with the climate system. Estimate the concentration of carbon dioxide (in ppm) at which we would expect to breach the DAI amount of warming. Assume a “mid-range” graybody parameter setting, i.e., term “B” is 1.25 W m-2 °C-1. Also assume that the pre-industrial carbon-dioxide concentration is 280 ppm and that the pre-industrial average global temperature is 288 K. Show your work.
- The atmospheric carbon-dioxide concentration is currently at about 414 ppm and is increasing by about 2 ppm per year. If we continue to increase carbon-dioxide concentration at this rate, how many years will it take until we commit ourselves to DAI, based on the climate sensitivity (i.e., the graybody parameter setting) considered above? If you were advising policy makers, how many years would you tell them we have to stabilize carbon-dioxide emissions and why? Show your work.
- Some scientists have argued that the threshold of 2°C is actually too high for DAI and that it should be a lower value. Re-work (c) and (d) assuming an alternative DAI of 1.5°C, and report the results. Is it too late to avoid DAI at this threshold? Show your work.
Lesson 4 Summary
In this lesson, we began to explore the use of theoretical models of the climate system. We saw that:
- A simple zero-dimensional energy balance model can be used to estimate the surface temperature of the Earth, as well as the response of surface temperatures to changes external (including human-induced perturbations). The model balances the incoming solar radiation absorbed at Earth's surface and the outgoing longwave radiation emitted from Earth's surface;
- A simple linear approximation can be used in the zero dimensional EBM to represent the outgoing longwave radiation, leading to a mathematical simplification and a simple formula for global surface temperature;
- Using the simplest, black body approximation for the outgoing longwave radiation gives a global surface temperature of about 255K, i.e., 18C below freezing—obviously way too cold;
- The gray body approximation provides a simple fix to the zero-dimensional EBM that incorporates, at least crudely, the atmospheric greenhouse effect;
- Using appropriate values of the gray body model coefficients, we can accurately predict both the Earth's surface temperature (roughly 288K, i.e., approximately 15°C), and the response of surface temperatures to perturbations such as increasing greenhouse gas concentrations (roughly 3°C for a doubling of atmospheric CO2).
This lesson also introduced us to the important concept of equilibrium climate sensitivity—a concept we will encounter again and again throughout this course.
Reminder - Complete all of the lesson tasks!
You have finished Lesson 4. Double-check the list of requirements on the first page of this lesson to make sure you have completed all of the activities listed there before beginning the next lesson.