Simple Climate Models, cont'd
Gray Body Variant of the Zero Dimensional EBM
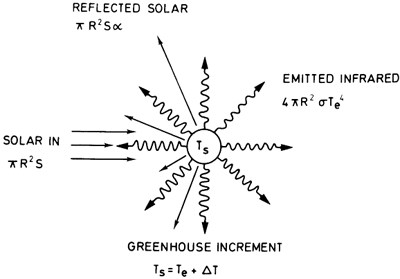
Even in the presence of the greenhouse effect, the net longwave radiation emitted out to space must balance the incoming absorbed solar radiation. So, we can think of the Earth system as still possessing an effective radiating temperature (Te), which is the black body temperature we calculated earlier with the zero-dimensional EBM and the black body parameter values for A and B, i.e., T = 255o K. It is the temperature Earth's surface has in the absence of any greenhouse effect. The outgoing longwave radiation to space is still given by . The atmosphere will have a temperature Te somewhere aloft in the cooler region of the mid-troposphere. If we like, we can think of the Earth as, on average, emitting temperature to space from this level; hence, we refer to the temperature as the effective radiating temperature.
When a greenhouse effect is present, the temperature at the surface, TS, will be substantially higher, however, due to the additional downward longwave radiation emitted by the atmosphere back down towards the Earth's surface.
We can attempt to account for this effect by simply changing the way we model the longwave radiation in the zero-dimensional EBM to account for the additional downward longwave radiation component.
Returning to the linearized form of the energy balance equation (i.e., equation (5) on the previous page), we will, therefore, now relax the assumption that A and B are given by their black body values. Instead, we will allow A and B to take on arbitrary values. This is a crude way of taking into account the fact that the Earth does not behave as a black body because the atmosphere has non-zero emissivity due to the presence of atmospheric greenhouse gases.
Simply put, we can tweak the values of A and B until they provide a good approximation. We refer to this generalized version of the black body approximation as the gray body approximation. The gray body model is a very crude way of accounting for the greenhouse effect in the context of a simple zero-dimensional model. In Lesson 5, we will build our way up to more realistic representations of the atmospheric greenhouse effect.
Various gray body parameter choices for A and B have been used by different researchers, in different situations. Since the gray body approximation is a linear approximation to a non-linear (Planck radiation) relationship, it is only valid over a limited range of temperatures about a given reference temperature. This means that a different set of parameters might be used for studying, e.g., the ice ages than would be used for studying, e.g., the early Cretaceous super greenhouse.
It turns out that the choices and yield realistic values for the current average temperature of the earth TS, and gives a value for the climate sensitivity — a concept we will define in the next section — that is consistent with mid-range IPCC estimates. We will, therefore, adopt these as our standard gray body parameter values, but we will also explore the impact of using alternative values a bit later.
Think About It!
Use the Online 0d EBM Application [1] to estimate the average temperature of the Earth for the "mid-range IPCC" gray body parameter values. What surface temperature do you find, and how does it compare with the previous black body estimate of Earth's surface temperature?
Click for answer.
You should have found that TS = 288o K in the gray body approximation.
This is roughly 33o C (or 60o F!) warmer than the black body value.
In other words, the greenhouse effect has the effect of warming Earth from a frigid average temperature of -18o C to a far more hospitable 15o C!
The Concept of Equilibrium Climate Sensitivity
Let us rewrite the equation energy balance equation (5) on the previous page in a slightly different form,
where Fin represents the total incoming radiative energy flux at the surface, which includes incoming short wave radiation, but also any potential changes in the downward longwave radiation towards the surface.
Let us now consider the response of Ts to an incremental change in Fin. Since the 2nd term in (7) is a constant, we simply have
We can also rewrite (8) as
The change in downward longwave radiation forcing associated with a change in CO2 concentration from a reference concentration, [CO2]0 to some new value, [CO2], can be approximated by the following relationship from a paper by Myhre et al. (1998) [2]
Now, let us further specify that we are interested in the change in radiative forcing resulting from a doubling of atmospheric CO2 concentrations. For a CO2 doubling, e.g., an increase from pre-industrial levels of 280 ppm to twice that value, 560 ppm,
We can define equilibrium climate sensitivity, s, as the change in temperature resulting from a doubling of pre-industrial CO2 concentrations; s has units of K (or equivalently degrees C, since differences in C and K are equal). To estimate s, we combine equations (8) and (11)
The equilibrium climate sensitivity is the equilibrium warming we expect in response to CO2 doubling. In the simple case of the 0d EBM, it is readily calculated through equation (12).
Think About It!
Using the formula above (12), estimate the equilibrium climate sensitivity s for both the black body model and our standard version of the gray body model. Record your answers.
Click for answer.
For the black body model, we have:
, i.e., approximately 1K
For the standard gray body model, we have:
, i.e., approximately 3K.
Think About It!
Let's now use the Online 0d EBM Application [1] again to estimate the climate sensitivity for these two cases, by explicitly varying the CO2 level until you achieve a CO2 doubling, and recording the warming that you observed. Compare to the results you calculated above directly from the formula for climate sensitivity for the 0d EBM.
Click for answer.
We find the same answers that we found earlier, namely that the black body models gives just under 1o C warming, while the gray body model gives roughly 3o C warming.
As we will see later, this is close to the best current available estimate of the warming expected from a doubling of CO2 concentrations.