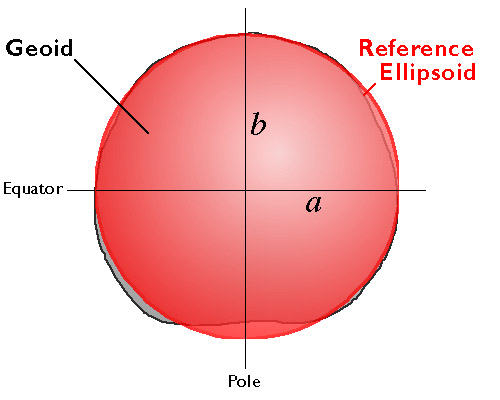
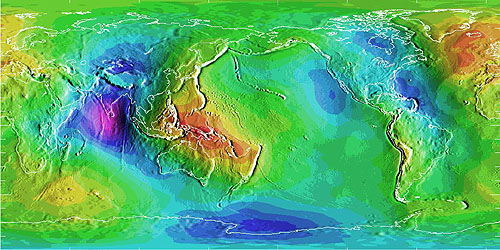
An ellipsoid is a three-dimensional geometric figure that resembles a sphere, but whose equatorial axis (a in Figure 2.15.1, above) is slightly longer than its polar axis (b). The equatorial axis of the World Geodetic System of 1984, for instance, is approximately 22 kilometers longer than the polar axis, a proportion that closely resembles the oblate spheroid that is planet Earth. Ellipsoids are commonly used as surrogates for geoids so as to simplify the mathematics involved in relating a coordinate system grid with a model of the Earth's shape. Ellipsoids are good, but not perfect, approximations of geoids. The map in Figure 2.15.2, below shows differences in elevation between a geoid model called GEOID96 and the WGS84 ellipsoid. The surface of GEOID96 rises up to 75 meters above the WGS84 ellipsoid over New Guinea (where the map is colored red). In the Indian Ocean (where the map is colored purple), the surface of GEOID96 falls about 104 meters below the ellipsoid surface.
Many ellipsoids are in use around the world. (Wikipedia presents a list in its entry on Earth Ellipsoids) Local ellipsoids minimize differences between the geoid and the ellipsoid for individual countries or continents. The Clarke 1866 ellipsoid, for example, minimizes deviations in North America. The North American Datum of 1927 (NAD 27) associates the geographic coordinate grid with the Clarke 1866 ellipsoid. NAD 27 involved an adjustment of the latitude and longitude coordinates of some 25,000 geodetic control point locations across the U.S. The nationwide adjustment commenced from an initial control point at Meades Ranch, Kansas, and was meant to reconcile discrepancies among the many local and regional control surveys that preceded it.
The North American Datum of 1983 (NAD 83) involved another nationwide adjustment, necessitated in part by the adoption of a new ellipsoid, called GRS 80. Unlike Clarke 1866, GRS 80 is a global ellipsoid centered upon the Earth's center of mass. GRS 80 is essentially equivalent to WGS 84, the global ellipsoid upon which the Global Positioning System is based. NAD 27 and NAD 83 both align coordinate system grids with ellipsoids. They differ simply in that they refer to different ellipsoids. Because Clarke 1866 and GRS 80 differ slightly in shape as well as in the positions of their center points, the adjustment from NAD 27 to NAD 83 involved a shift in the geographic coordinate grid. Because a variety of datums remain in use, geospatial professionals need to understand this shift, as well as how to transform data between horizontal datums.
The preceding statement remains true despite the fact that NAD 83 will soon be discontinued as part of the National Geodetic Survey's ongoing modernization of the U.S. National Spatial Reference System. The switch from a "passive" ellipsoid-based reference system to a GPS-based dynamic system was planned for 2022, but it has since been delayed until 2024 or -25. Visit the National Geodetic Survey for the latest information.