Point locations are specified in terms of (a) their positions relative to some coordinate system grid and (b) their heights above or below some reference surface. Obviously, the elevation of a stationary point depends upon the size and shape of the reference surface (e.g., mean sea level) upon which the elevation measurement is based. In the same way, a point's position in a coordinate system grid depends on the size and shape of the surface upon which the grid is draped. The relationship between a grid and a model of the Earth's surface is called a horizontal datum. GIS specialists who are called upon to merge data sets produced at different times and in different parts of the world need to be knowledgeable about datum transformations.
NAD 27 to NAD 83
In the U.S., the two most frequently encountered horizontal datums are the North American Datum of 1927 (NAD 27) and the North American Datum of 1983 (NAD 83). The advent of the Global Positioning System necessitated an update of NAD 27 that included (a) adoption of a geocentric ellipsoid, GRS 80, in place of the Clarke 1866 ellipsoid; and (b) correction of many distortions that had accrued in the older datum. Bearing in mind that the realization of a datum is a network of fixed control point locations that have been specified in relation to the same reference surface, the 1983 adjustment of the North American Datum caused the coordinate values of every control point managed by the National Geodetic Survey (NGS) to change. Obviously, the points themselves did not shift on account of the datum transformation (although they did move a centimeter or more a year due to plate tectonics). Rather, the coordinate system grids based upon the datum shifted in relation to the new ellipsoid. And because local distortions were adjusted at the same time, the magnitude of grid shift varies from place to place. The illustrations below compare the magnitude of the grid shifts associated with the NAD 83 adjustment at one location and nationwide.
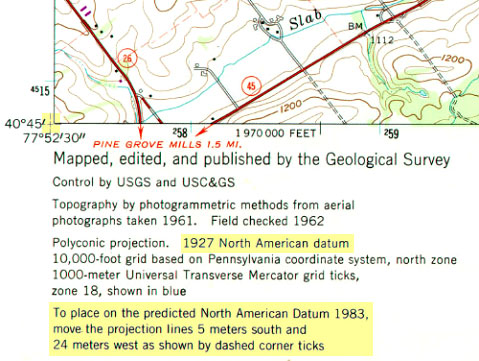
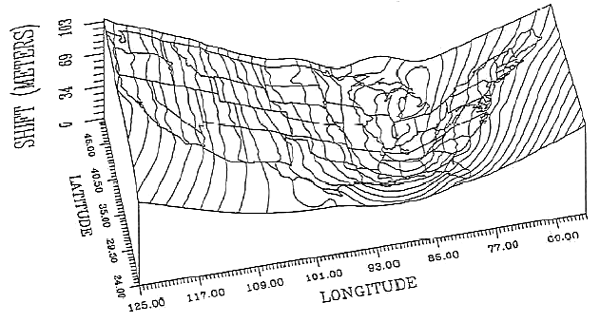
Given the irregularity of the shift, NGS could not suggest a simple transformation algorithm that surveyors and mappers could use to adjust local data based upon the older datum. Instead, NGS created a software program called NADCON (Dewhurst 1990, Mulcare 2004) that calculates adjusted coordinates from user-specified input coordinates by interpolation from a pair of 15° correction grids generated by NGS from hundreds of thousands of previously-adjusted control points.
GPS Data and WGS 84
The U.S. Department of Defense created the Global Positioning System (GPS) over a period of 16 years at a startup cost of about $10 billion. GPS receivers calculate their positions in terms of latitude, longitude, and height above or below the World Geodetic System of 1984 ellipsoid (WGS 84). Developed specifically for the Global Position System, WGS 84 is an Earth-centered ellipsoid which, unlike the many regional, national, and local ellipsoids still in use, minimizes deviations from the geoid worldwide. Depending on where a GIS specialist may be working, or what data he or she may need to work with, the need to transform GPS data from WGS 84 to some other datum is likely to arise. Datum transformation algorithms are implemented within GIS software as well as in the post-processing software provided by GPS vendors for use with their receivers. Some transformation algorithms yield more accurate results than others. The method you choose will depend on what choices are available to you and how much accuracy your application requires.
Unlike the plane transformations described earlier, datum transformations involve ellipsoids and are therefore three-dimensional. The simplest is the three-parameter Molodenski transformation. In addition to knowledge of the size and shape of the source and target ellipsoids (specified in terms of semimajor axis, the distance from the ellipsoid's equator to its center, and flattening ratio, the degree to which the ellipsoid is flattened to approximate the Earth's oblate shape), the offset between the two ellipsoids needs to be specified along X, Y, and Z axes. The window shown below (Figure 2.19.3) illustrates ellipsoidal and offset parameters for several horizontal datums, all expressed in relation to WGS 84.
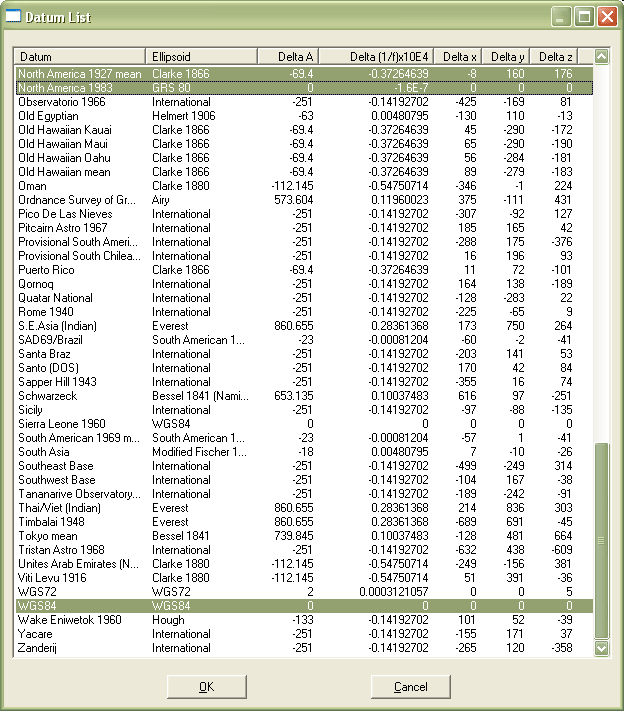
For larger study areas, more accurate results may be obtained using a seven-parameter transformation that accounts for rotation as well as scaling and offset.
Finally, surface-fitting transformations like the NADCON grid interpolation described above yield the best results over the largest areas.
For routine mapping applications covering relatively small geographic areas (i.e., larger than 1:25,000), the plane transformations described earlier may yield adequate results when datum specifications are unknown and when a sufficient number of appropriately distributed control points can be identified.
