Ideal Behavior

An ideal gas is an imaginary gas that satisfies the following conditions:

• Negligible interactions between the molecules,
• Its molecules occupy no volume (negligible molecular volume),
• Collisions between molecules are perfectly elastic — this is, no energy is lost after colliding.

We recognize that this fluid is imaginary because — strictly speaking — there are no ideal gases. In any fluid, all molecules are attracted to one another to some extent. However, the ideal approximation works best at some limiting conditions, where attraction forces can be considered to be weak. In fact, ideal behavior may be approached by real gases at low pressures (close to atmospheric) and high temperatures. Note that at low pressures and high temperatures, the distance between any pair of gas molecules is great. Since attraction forces weaken with distance, we have chosen a condition where attraction forces may be neglected. In conclusion, we consider a gas ideal when each molecule behaves as if it were alone — molecules are so far apart from each other that they are not affected by the existence of other molecules.

The behavior of ideal gases has been studied exhaustively and can been extensively described by mathematical relationships.

For a given mass of an ideal gas, volume is inversely proportional to pressure at constant temperature, i.e.,

$$v\alpha \frac{1}{P}(at constant temperature)$$(6.1)

This relationship is known as Boyle’s Law. Additionally, volume is directly proportional to temperature if pressure is kept constant, i.e.,

$$v\alpha T(at constant pressure)$$ (6.2)

This relationship is known as Charles’ Law. By combining both laws and recognizing “R” (the universal gas constant) as the constant of proportionality, we end up with the very familiar equation:

<$$Pv=nRT$$ (6.3)

This represents the equation of state (EOS) of an ideal gas. Numerical values of “R” depend on the system of units that is used:

$$R10.731\frac{{\text{psia ft}}^{\text{3}}}{\text{lbmol R}}8.3144\frac{\text{Joule}}{\text{gmole K}}1.9872\frac{\text{cal}}{\text{gmole K}}$$ $$R1.314\frac{{\text{atm ft}}^{\text{3}}}{\text{lbmol R}}0.7302\frac{{\text{atm ft}}^{\text{3}}}{\text{lbmol R}}1.9869\frac{\text{BTU}}{\text{lbmol R}}$$

If we construct the P-v diagram for an ideal gas at a given temperature, we end up with the isotherm shown in Figure 6.2.

Figure 6.2: P-v Isotherm for an Ideal Gas

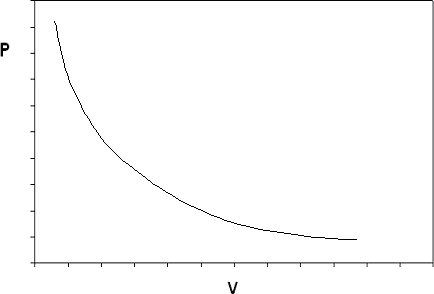
The ideal gas model predicts two limiting fluid behaviors: first, that the volume of the gas becomes very large at very low pressures $v\to \infty$ as $P\to 0$ , a concept that agrees with what we know from our experience in the physical world). And second, $v\to \infty$ as $P\to 0$ (the volume of matter just “vanishes” if the pressure is high enough: this concept we would not be as willing to accept). These two behaviors are a consequence of the assumptions made in the ideal gas model.