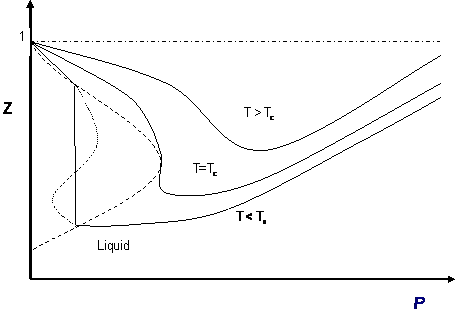It comes as no surprise that cubic equations of state yield three different roots for volume and compressibility factor. This is simply because they are algebraic equations, and any nth order algebraic equation will always yield “n” roots. However, those “n” roots are not required to be distinct, and that is not all: they are not required be real numbers, either. A quadratic expression (n = 2) may have zero real roots (e.g., x2 + 1 = 0); this is because those roots are complex numbers. In the case of cubic expressions (n = 3), we will either have one or three real roots; this is because complex roots always show up in pairs (i.e., once you have a complex root, its conjugate must also be a solution.) In our case, and because we are dealing with physical quantities (densities, volumes, compressibility factors), only real roots are of interest. More specifically, we look for real, positive roots such that in the case of molar volume and in the case of compressibility factor.
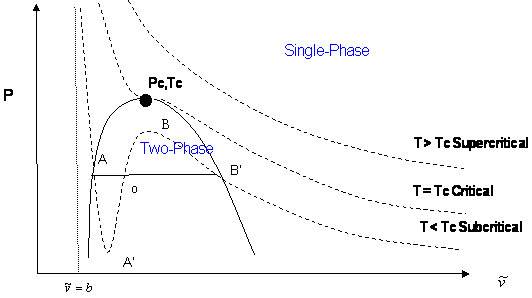
In a cubic equation of state, the possibility of three real roots is restricted to the case of sub-critical conditions (T < Tc), because the S-shaped behavior, which represents the vapor-liquid transition, takes place only at temperatures below critical. This restriction is mathematically imposed by the criticality conditions. Anywhere else, beyond the S-shaped curve, we will only get one real root of the type . Figure 10.1 illustrates this point.
Let us examine the three cases presented in Figure 10.1:
- Supercritical isotherms (T > Tc): At temperatures beyond critical, the cubic equation will have only one real root (the other two are imaginary complex conjugates). In this case, there is no ambiguity in the assignment of the volume root since we have single-phase conditions. The occurrence of a unique real root remains valid at any pressure: any horizontal (isobaric) line cuts the supercritical isotherm just once in Figure 10.1.
- Critical isotherm (T = Tc): At the critical point (P = Pc), vapor and liquid properties are the same. Consequently, the cubic equation predicts three real and equal roots at this special and particular point. However, for any other pressure along the critical isotherm (P < Pc or P > Pc,) the cubic equation gives a unique real root with two complex conjugates.
- Subcritical isotherm (T < Tc): Predictions for pressures within the pressure range for metastability (PA’ < P < PB’) or for the saturation condition (P = Psat) will always yield three real, different roots. In fact, this is the only region in Figure 10.1 where an isobar cuts the same isotherm more than once. The smallest root is taken as the specific volume of the liquid phase; the largest is the specific volume of the vapor phase; the intermediate root is not computed as it is physically meaningless. However, do not get carried away. Subcritical conditions will not always yield three real roots of the type . If the pressure is higher than the maximum of the S-shaped curve, PB, we will only have one (liquid) real root that satisfies . By the same token, pressures between 0 < P < PA’ yield only one (vapor) root. In the case of PA’ being a negative number, three real roots are to be found even for very low pressures when the ideal gas law applies. This can be seen in Figure 10.1 as well. The largest root is always the correct choice for the gas phase molar volume of pure components.
Most of these considerations apply to the cubic equation of state in Z (compressibility factor). The most common graphical representation of compressibility factor is the well-known chart of Standing and Katz, where Z is plotted against pressure. Standing and Katz presented their chart for the compressibility factor (Z) of sweet natural gases in 1942. This chart was based on experimental data. Graphical determination of properties was widespread until the advent of computers, and thus the Standing and Katz Z-chart became very popular in the natural gas industry. Typical Standing and Katz charts are given for high temperature conditions (T > Tc or Tr > 1). Figure 10.2, using a cubic equation of state for a pure gas, presents the qualitative behavior of the solution of Z versus pressure. Isotherms (T > Tc) show the typical qualitative behavior we are accustomed to seeing in the Standing and Katz chart. Cases T < Tc (Tr < 1) are not as familiar to us, as they were not considered by Standing and Katz. For such isotherms, it is clear that you come up with two values of Z (liquid, gas) at saturation conditions.