Course Outline
Introduction and Purpose
Overview
Module Goal
To sensitize you to the central role that phase behavior plays in the petroleum extraction processes.
Module Objective
At the completion of this module, you should be able to describe, in concrete terms, how knowledge of fluid phase behavior impacts specific aspects of the process design and/or operations you are engaged in.
Introduction
The basic essence of engineering is to harness the tremendous energy of the universe, in its latent or potent form, to resolve socio-economic problems. Most often than not in the process, energy must be converted from its natural form into a form that is more amenable to human utilization. Petroleum and natural gas engineering is no different. It is a discipline focused on efficiently extracting the petroleum buried deep within the earth and getting it to where it is needed. The petroleum fluids of particular interest to the petroleum and natural gas engineers are crude oil and natural gas. The term crude oil is used broadly here as to encompass the different forms of petroleum liquids that are used for energy and other purposes.
Natural gas and crude oil are naturally occurring hydrocarbon mixtures; generally they are referred to as petroleum fluids. These fluids are found underground at elevated pressure and temperature conditions. Petroleum fluids are composed principally of hydrocarbons; various non-hydrocarbon components, such as nitrogen, carbon dioxide, and hydrogen sulfide, may also be present.
Producing, separating, transporting, and storing petroleum fluids are the primary responsibilities of a petroleum and natural gas engineer. Therefore, we make no mistake when we refer to natural gas and petroleum engineers as petroleum fluid engineers. These engineers deal with hydrocarbon fluids to make a living. As a consequence, they may very well be referred to as hydrocarbon fluid engineers. One cannot overemphasize the importance of the primary fluids — oil and natural gas — to the modern industrial society. Indeed, modern man’s reliance upon natural gas and crude oil as the primary source of energy is such that these fluids are absolutely critical to the operation of today’s industrial society. It is fair to assume that you, the reader, are interested in hydrocarbon fluids production.
At every stage of the petroleum exploration and production business, a hydrocarbon fluid engineer is needed. Hydrocarbon fluid engineers might find themselves dealing with activities such as reserve evaluations, drilling operations, reservoir analyses, production operations, and gas processing. They are, therefore, called upon to deal with a wide spectrum of activities, mostly dealing with fluid handling and the associated facilities.
Most of the fluid handling protocols require the engineer to know a priori how the fluids will behave under a wide range of pressure and temperature conditions, particularly in terms of their volumetric and thermophysical properties. For example, the engineers should know if the reservoir contains a dry gas, a wet gas, or a gas-condensate before they design the surface production facility. This is collectively termed fluid phase behavior. It is therefore, not an overstatement to say that a thorough understanding of hydrocarbon fluid phase behavior is essential for the work of a petroleum and natural gas engineer. Phase behavior has defining implications in petroleum and natural gas engineering processes. Pressure, volume, and temperature (PVT) relations are required in simulating reservoirs, evaluating reserves, forecasting production, designing production facilities, and designing gathering and transportation systems.
En route from a subsurface reservoir to man’s energy extracting combustion processes, a hydrocarbon molecule goes through various phase- and property-altering intermediate stages. These properties are crucial in designing and operating the processes efficiently and optimally. Phase behavior thermodynamics gives us the tools needed for gaining the desired understanding of how fluids behave at any of those stages.
Questions?
If you have questions at any time during this lesson, please feel free to post them to the Course Introduction Discussion Forum. (Click on the Discussions tab under Home in Canvas to access our course discussion forums.)
Why Study Phase Behavior?
Natural gas and crude oil are naturally occurring hydrocarbon mixtures that are found underground and at elevated conditions of pressure and temperature. They are generally referred to as petroleum fluids. Petroleum fluids are principally made up of hydrocarbons; but few non-hydrocarbon components may be present such as nitrogen, carbon dioxide and hydrogen sulfide.
We make no mistake when we refer to Natural Gas and Petroleum Engineers as Fluid Engineers. This is, engineers that deal with fluids to make a living. Moreover, we specialize in two special fluids whose importance to the society cannot be overstated--indeed, humankind rely on natural gas and crude oil as the premier source of energy that keeps the society operative. As a consequence, we may very well be titled as Hydrocarbon Fluid Engineers. That is everything we are basically about. At every stage of the oil business, a Hydrocarbon Fluid engineer is required. This is, reservoir analyses, drilling operation, production operation, processing, among others, reveal the wide spectrum of areas where an engineer with expertise on hydrocarbon fluids is fundamental.
This said, what can be more important for a Hydrocarbon Fluid Engineer than understanding how these fluids behave?
It is not an overstatement to say that a through understanding of hydrocarbon phase behavior is quintessential for the Petroleum and Natural Gas Engineer. Phase Behavior has many implications in natural gas and petroleum engineering. Pressure, volume, temperature (PVT) relations are required in simulating reservoirs, evaluating reserves, forecasting production, designing production facilities and designing gathering and transportation systems.
Every hydrocarbon molecule in the reservoir is to embark on a fascinating journey from beneath the earth, passing through a great deal of intermediate stages, to be finally dumped into our atmosphere upon combustion (release of energy). Phase Behavior is the part of thermodynamics that gives us the tools for the complete understanding of how fluids behave at any of those stages. Let us be the witnesses of this exciting journey.
Summary
Regardless of the aspect of petroleum extraction process — be it drilling, reserve estimation, reservoir performance analysis, reservoir simulation, tubing flow hydraulics, gathering design, gas-liquid separation, oil and gas transmission, oil and gas metering or quality control — a good predictive knowledge of phase behavior is called for. This course will help you to acquire this knowledge. You may never have to develop computer routines for doing many of the predictive calculations pertaining to hydrocarbon fluid phase behavior; nevertheless, the knowledge base developed in this course will help you develop the understanding needed to be an intelligent user of commercial software packages and ask the right questions that your responsibility as an engineer demands.
Action Item
Write a paragraph or two describing, very briefly, your educational background and practical experience, including your knowledge of phase behavior (if any) and how you apply or have applied this subject matter in your current or recent work assignments. Post your paragraph(s) to the Module 1 Message Board in our online course environment Canvas [1]. From our Canvas course environment, click on the In Touch tab.
- Scroll down to the "Message Boards" section, then click on the link for Module 1 Message Board.
- In the message space provided, type in your paragraph(s) or paste them in if you drafted them first in another application.
- Click on the Save button to post your message.
- Click on the other student postings in the listing of threaded messages to learn more about your fellow classmates.
Phase Diagrams, Part I
Module Goals
Module Goal: To familiarize you with the basic concepts of phase diagrams as a means of representing thermodynamic data.
Module Objective: To highlight the basic description of phase diagrams of single-component systems.
Introduction
One of the primary challenges that we face as engineers is how to communicate large quantities of complex information to our peers and superiors. For instance, we may need to report what thermodynamic changes our working fluid is undergoing. Here, the familiar saying: A picture is worth a thousand words applies. Although most non-engineers believe that the only language an engineer speaks is mathematics, in actuality, the most effective means that engineers use to communicate information involves the use of pictures or diagrams. Phase behavior is not an exception. In phase behavior thermodynamics, phase diagrams are used precisely for this purpose.
Phase Diagram:
A phase diagram is a concise graphical method of representing phase behavior of fluids. It provides an effective tool for communicating a large amount of information about how fluids behave at different conditions.
First of all, let us classify fluids into two broad groups on the basis of the number of components that are present in the system: pure component systems and mixtures.
Two Classes of Fluids
-
Pure-component systems
-
Mixtures
Although this classification may seem trivial at a first glance, it recognizes the paramount influence of composition on the phase behavior of a fluid system. Whereas for a single-component system, composition is not a variable and therefore cannot influence behavior, the behavior of a mixture is strongly controlled by composition. In fact, as the number of components in the system increases, the complexity of the phase diagram increases as well. Therefore, the simplest form of a phase diagram is that of a system made of only one component (a pure-component system).
Pure-component Systems
Let us start with a well-known single component system: water — the most plentiful substance on earth. What is the behavior of water under different conditions of pressure and temperature? Or even more specific, is there a single answer to the question: what is the boiling point of water? Most people would say, “of course, 100 °C”, but a more accurate response would pose a clarifying question: “At what pressure?” It is common knowledge that water boils at 100 °C (212 °F) at atmospheric pressure. By requiring a pressure specification in order to uniquely define the boiling point of water, we are acknowledging that the boiling temperature of a pure substance is pressure-dependent. In reality, we are also implicitly applying a very useful thermodynamic principle, the Gibbs Rule, but this will be the topic for later discussion.
In thermodynamics, we refer to the Normal Boiling Point as the boiling temperature of a fluid at 1 atm of pressure (that is, atmospheric pressure.) Therefore, 100 °C (212 °F) is the normal boiling point of water.
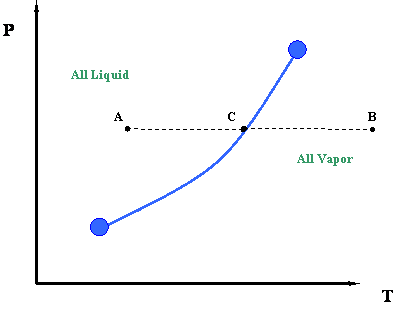
What if we want to communicate this idea? We would like to communicate the concept that the temperature at which water boils varies with pressure. What about a picture to represent this information? Here is our first phase diagram, Figure 2.1. Whereas several sentences may be required to describe the variability of the boiling point of water, the single line shown in Figure 2.1 is adequate. What does Figure 2.1 tell us? It tells us that the boiling temperature of a liquid increases as pressure increases. In other words, it says that the vapor pressure of a liquid increases as temperature increases. That is to be expected because as the temperature increases, more liquid molecules are able to escape into the vapor phase, thus increasing the pressure that the aggregate of all vapor molecules exerts on the system (i.e. vapor pressure).
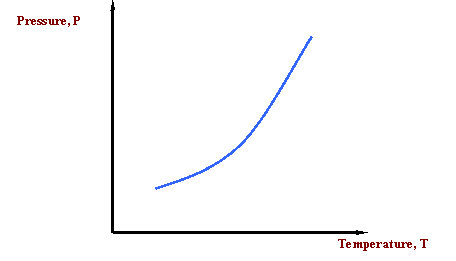
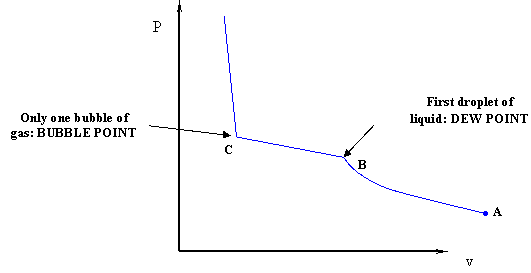
The curve in Figure 2.1 is called the vapor pressure curve or boiling point curve. The line also represents the dew point curve and the bubble point curve; one on top of the other. This curve represents the transition between the vapor and liquid states.
Definition of Basic Terms
Vapor Pressure: The pressure that the vapor phase of a fluid exerts over its own liquid at equilibrium at a given temperature.
Dew Point: The pressure and temperature condition at which an infinitesimal quantity of liquid (a droplet) exists in equilibrium with vapor. It represents the condition of incipient liquid formation in an initially gaseous system. Notice that it can be also visualized as a “liquid system” where all but an infinitesimal quantity of liquid has been vaporized.
Bubble Point: The pressure and temperature condition at which the system is all liquid, and in equilibrium with an infinitesimal quantity (a bubble) of gas. This situation is, in essence, the opposite of that of the dew point.
Note:
For single-component systems, one single curve represents all three of these conditions (vapor pressure, dew point and bubble point conditions) simply because Vapor Pressure = Dew Point = Bubble Point for unary systems.
In Figure 2.1, once a saturation pressure has been selected, there is one (and only one) saturation temperature associated with it. This is only true for a single component system. In other words, this is the only temperature (at the given pressure), at which liquid and gas phase will co-exist in equilibrium. The rule that governs the uniqueness of this point, for a single-component system, is called the Gibbs Phase Rule. This is the second time we have mentioned this rule, pointing to its great importance in phase behavior. Let us postpone any detailed discussion of the Gibbs Phase Rule until later.
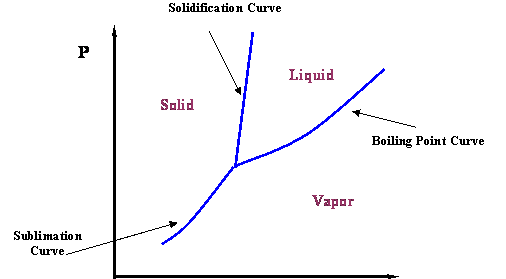
The vapor curve, shown in Figure 2.1, represents the transition between the vapor and liquid states for a pure component. Obviously, this is not the whole story. If we cool the liquid system, it makes sense to expect ice to form (a solid phase). We can communicate this new idea by adding more information to Figure 2.1. In fact, there is a line that defines the liquid-solid transition; it is called the solidification (or melting) curve (see Figure 2.2). Furthermore, even though it is counter-intuitive, it is possible to go from solid to vapor without going through a liquid state, if the pressure is low enough. This information can be added to the diagram by including the sublimation curve. Thus, Figure 2.2 represents a more complete phase diagram for a pure-component system.
See how more and more information can be represented within the limits of the phase diagram. As petroleum and natural gas engineers, we focus our attention on the Boiling Point Curve, as it represents the transition between liquid and gas, the phases with which we deal most often. Let us focus our attention on it.
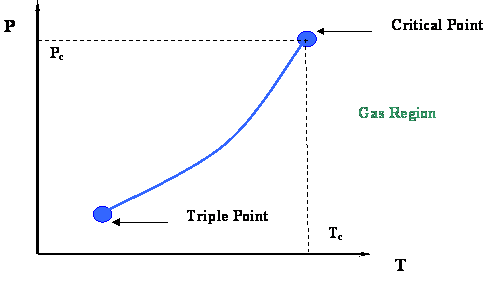
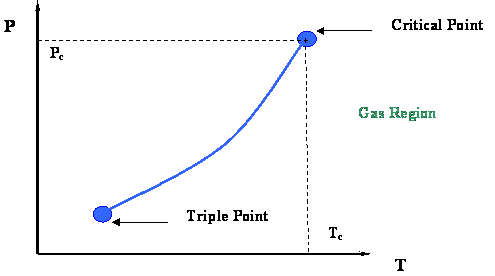
Figure 2.3 presents a P-T diagram representing the vapor pressure curve and its extremities. Two very important thermodynamic points bound the vapor pressure curve: the Critical Point at its upper end and the Triple Point at its lower end.
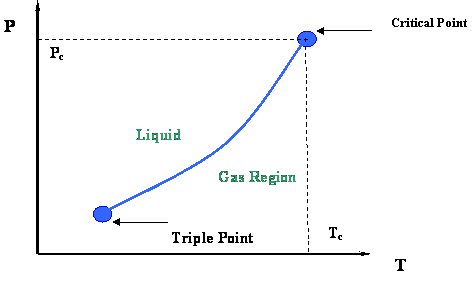
The Triple Point is the meeting point of the vapor pressure, solidification and sublimation curves (see Figure 2.2); hence, it represents the only condition at which all three phases of a pure substance (solid, liquid and gas) can co-exist in equilibrium.
At the Critical Point, gas and liquid are in equilibrium without any interface to differentiate them; they are no longer distinguishable in terms of their properties. As we recall, the only location on the P-T diagram where liquid and gas can be found together in equilibrium is along the vapor pressure curve. Hence, the critical point is clearly the maximum value of temperature and pressure at which liquid and vapor can be at equilibrium. This maximum temperature is called the critical temperature (Tc); the corresponding maximum pressure is called the critical pressure (Pc).
Let us conclude this first module by highlighting the most important properties of the critical point of pure substances, as shown below. The next module will be providing more details of interest that are embedded in Figure 2.3.
Properties Of The Critical Point (Tc,Pc) (For Pure Substances):
- Temperature and pressure for which liquid and vapor are no longer distinguishable.
- For T > Tc, liquid and vapor will not co-exist, no matter what the pressure is.
- For P > Pc, liquid and vapor will not co-exist, no matter what the temperature is.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
Speculate on what the difference would be between phase diagrams (P-T curve) of various pure component systems. Write a paragraph or so on what you believe the differences are and why.
-
What should be the differences in the diagrams in question 1? Are the dew points the same? What about the bubble points? And their critical points?
Phase Diagrams, Part II
Module Goals
Module Goal: To familiarize you with the basic concepts of phase diagrams as a means of representing thermodynamic data.
Module Objective: To familiarize you with the use of P-T and P-v diagrams.
Vapor Pressure Curve
From the last module you will recall that the vapor-pressure curve (Figure 2.3) and its extremities were examined. That figure is presented in this module in Figure 3.1. We concluded that two very important thermodynamic points bound the vapor pressure curve: the Critical Point at its upper end and the Triple Point at its lower end.
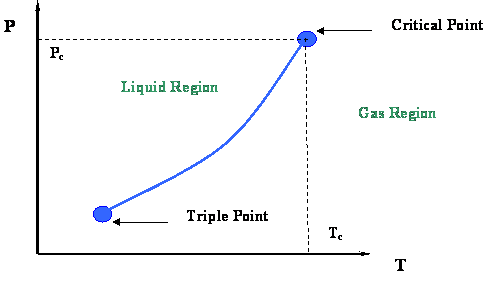
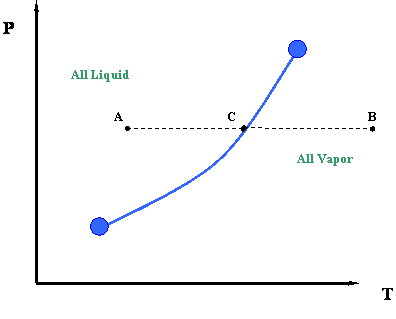
Now let us take a second look at this figure. We can better understand the information represented by the vapor pressure curve by looking at the process of isobaric heating. This is illustrated by line ACB in Figure 3.2. The term “isobaric” pertains to a constant pressure process. By isobaric heating process, we then mean a “constant pressure addition of heat into a system.”
Such a process can be described as follows. Starting at point A and moving towards point C at constant pressure, we add heat to the system. By adding this heat, we cause a temperature increase in the system (Temperature at C > Temperature at A.). At point C, which lies above the vapor pressure or boiling point curve, we encounter a phase change. To the left of point C, at lower temperatures, exists only liquid. To the right of point C, at higher temperatures, there is only vapor. Therefore, a sharp discontinuity in density exists at point C. During this transition, from liquid to vapor, we will notice that the heat that we add to the system does not cause any temperature increase, and in fact, temperature and pressure conditions remain constant during the transition represented by the vapor curve. In other words, even though we are adding heat, the system remains at the pressure and temperature associated with point C until the whole phase transition has taken place — i.e., until all the vapor is converted to liquid. Instead of working to increase liquid temperature, this heat serves to move liquid molecules apart until all liquid has become vapor.
Up to this point, we saw that the heat added before the system reached the phase transition was used to raise the temperature of the substance. However, the heat that we are adding right now, during the phase transition, is not causing any temperature increase (hence it is said to be hidden heat or latent heat of vaporization). Therefore, we differentiate between two kinds of heat: sensible heat and latent heat.
Sensible Heat: Its main purpose is to cause an increase in temperature of the system.
Latent Heat: It serves only one purpose: to convert the liquid into vapor. It does not cause a temperature increase.
In fact, the name “latent” suggests “hidden.” Here, we are adding heat to the system but are not seeing its effect in terms of temperature increase. The heat that is needed to transform one mole of saturated liquid into vapor is known as the latent molar heat of vaporization: 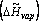
Once we have converted all the liquid into vapor (i.e., we supplied all the necessary latent heat to accomplish this), we may continue to add more heat. If we do so, the temperature will rise again and we will end at point B (Figure 3.2). This heat is also sensible since it is causing the temperature of the system to rise.
It is interesting to note that, in order to reverse the process from point B to point A, we will have to remove the exact amount of heat that we had added before. This is a basic consequence of an energy balance principle. We call such a reverse process an isobaric cooling process. We will have to remove some sensible heat in order to cool the vapor from point B to C, and then we will remove all the latent heat of the vapor to condense it into liquid (transition at point C). Finally, we will also need to remove more sensible heat from the system for the cooling of the liquid from point C to point A.
In the previous two processes, from A to B or vice versa, we had to cross the phase boundary represented by the vapor pressure curve. However, this is not the only thermodynamic path that is available for us to go from A to B. Figure 3.3 depicts another possible path.
Instead of doing the whole process isobarically, we may devise a new path that may also accomplish the goal of taking the system from a condition ‘A’ to a condition ‘B.’ Consider the path ADEB that is shown in Figure 3.3.
Sequence of Paths
- Path AD: Isothermal compression
- Path DE: Isobaric heating
- Path EB: Isothermal expansion
There is something remarkable about this new path. Unlike the previous path, notice that we do not cross the phase boundary at all. The consequences of taking this new road may seem astonishing at first glance: we went from an all-liquid condition (point A) to an all-vapor condition (point B) without any sharp phase transition. In fact, along the path ADEB there is NO phase transition because we never crossed the phase boundary. Since the phase boundary represents a sharp discontinuity in density (and other physical properties), the fact that we are not crossing it tells us that as we go, there is actually a gradation in density (from a liquid like, or high-density at point A to a gas like, or low-density at point B) instead of a sharp change from the high liquid density to the low gas density.
We were able to do so because we went above the critical conditions. In the vicinity of and beyond critical conditions, we are no longer able to distinctly label the single-phase condition as either “liquid” or “gas”. Under these conditions, any transition takes place gradually without any differentiation between a ‘liquid’ and a ‘gas’ phase. We call this fluid, which we cannot define either as a liquid or as a gas, a supercritical fluid. In terms of density, a supercritical fluid may be described, at the same time, as a light liquid (its density is not as high as the liquid density) and a heavy gas (its density is not as low as the typical gas density of the given substance). The behavior of fluid around this area is an active and interesting area of current research.
In summary, for a pure substance, you can avoid having an abrupt phase transition (such as the one described by the path ACB) by going around the critical point (path ADEB). Keep in mind that any path that crosses the vapor pressure curve (ACB) will undergo a phase transition.
PV Diagram for Pure Systems
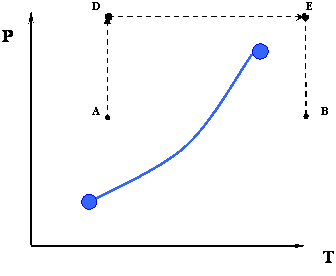
In the previous discussion, we used the P-T diagram and were not concerned about changes in the volume of the system. If we want to follow changes in volume, we may construct P-v or T-v diagrams, in which we hold temperature (T) or pressure (P) constant. Let us consider the case of a P-v Diagram (Figure 3.4).
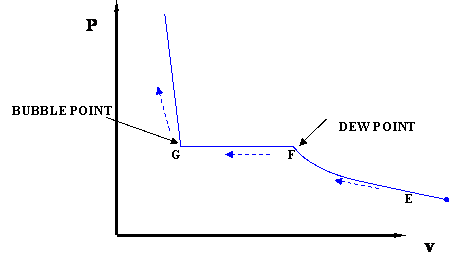
In this case temperature is being held constant; our substance is undergoing an isothermal compression process. Starting at E (all-vapor condition), an increase in pressure will result in a rather significant reduction in volume since the gas phase is compressible. If we keep compressing isothermally, we will end up at point F, where the gas will be saturated and the first droplet of liquid will appear. We have come to the two-phase condition, where liquid (L) and vapor (V) co-exist in equilibrium, for the first time, albeit an infinitesimal amount of liquid.
Once we reach the two-phase condition, what happens is not intuitive. While we keep on compressing by decreasing the volume (path F-G,) the pressure of the system remains constant; this condition continues until all the vapor has become liquid. Point G represents the last condition of liquid and vapor (L+V) coexistence, saturated liquid condition (liquid in equilibrium with an infinitesimal amount of vapor.) Once we have only liquid, if we keep on compressing (i.e., attempting to reduce liquid volume) we will observe a rapid increase in pressure, as indicated by the steep slope in the P-v diagram. This is because liquid is virtually incompressible, hence, a great deal of pressure is needed to cause a small reduction in volume.
It is important to recognize some points of this process. If we recall our previous definitions of basic concepts, we will recognize point F, where only a tiny quantity of liquid exists in an otherwise completely gaseous system (the dew point of the system at the given temperature). Similarly, Point G is the bubble point; only an infinitesimally small bubble of vapor exists in an otherwise liquid system.
But wait a second. Let us try to compare Figure 3.4 with Figure 3.2. Can we relate them to each other? Where is path F-G in Figure 3.4 represented in Figure 3.2 (repeated below)?
The answer is, path F-G is represented by one point in Figure 3.2; that is, point C. Recall, for a single-component system, dew points and bubble points are identical. During a phase transition, both pressure and temperature must remain constant for pure components.
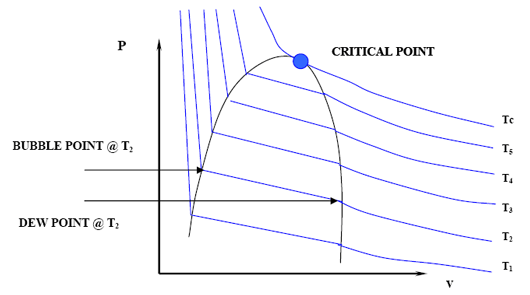
Now, if we want to generate all the possible points that make up the vapor pressure curve in Figure 3.2, we would need to repeat the experiment for different temperatures. We would end up with a family of isotherms (each similar to the one presented in Figure 3.4). This is represented in Figure 3.5.
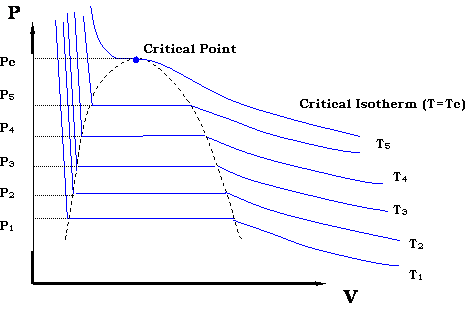
The zone where the isotherms become flat delineates the two-phase region. It is clearly seen that by plotting all the pairs in that zone (P1,T1), (P2,T2)… (Pc, Tc) we will be able to reproduce Figure 3.2.
If we now draw a line through all the Bubble Points in Figure 3.5, and then draw a line connecting all the Dew Points, we will end up with the Bubble Point Curve and the Dew Point Curve, respectively. It is clear that the two curves meet at the critical point (Pc, Tc). Furthermore, the two curves delineate the phase envelope, which contains the 2-phase region inside. If we “clean” Figure 3.5 a little, we end up with the phase envelope that is shown in Fig. 3.6.
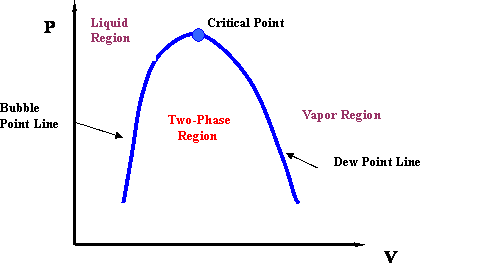
If you carefully follow the trend of the critical isotherm (@ T = Tc in Fig. 3.5), you will realize that it has a point of inflexion (change of curvature) at the critical point. Furthermore, the critical point also represents the maximum point (apex) of the P-v envelope. Mathematically, this information is conveyed by the expressions:
$$\left(\frac{\partial P}{\partial \vec{V}}\right)_{P C, T C}=\left(\frac{\partial^{2} P}{\partial \vec{V}^{2}}\right)_{P C T C}=0$$
which are usually known as the criticality conditions. These conditions are always satisfied at the critical point. We will comment more on this after we begin the discussion on Equations of State (EOS) — semi-empirical relationships that mathematically model the P-v-T behavior of fluids.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
- Explain in your own words (no more than a paragraph) why the 2-Phase segment of the P-v isotherm should correspond to one single point in the P-T diagram.
- What about the critical point in the P-T diagram? Which P-v isotherm could that correspond to?
- Take two different hydrocarbons (say, C1 and C2) and compare their P-T vapor pressure curves. What do you notice? As you saw in the previous module, those P-T curves will be found at different conditions of pressure and temperature. But more than that, what can you comment about the slopes of both curves? Are they different? Why? Speculate.
Phase Diagrams, Part III
Module Goals
Module Goal: To familiarize you with the basic concepts of Phase Diagrams as a means of representing thermodynamic data.
Module Objective: To introduce you to the additional complexity brought about by the presence of one or more additional components.
Binary Systems
Thus far, we have focused our attention on single-component systems (also called unary, one-component, or pure-component systems). However, real-life systems are never single-component; they are multicomponent systems. The simplest of this category is the binary system. The good news, however, is that the behavior of multicomponent systems are quite similar to that of binary systems. Therefore, we will focus on binary systems, since they are easier to illustrate.
Let us place two gases (A and B) in an isothermal cell. As we did before, we will keep temperature constant during this experiment (shown in Fig. 4.1)
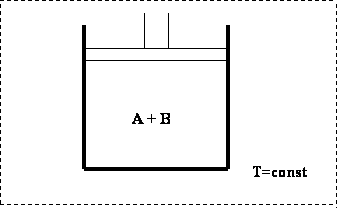
If we move the piston down, we would compress the gasses, causing a decrease in volume. In such a scenario, an increase in pressure would occur. The process starts at point A, as shown in Figure 4.2, an all-vapor condition.
Nothing here is new regarding the compression of the vapor itself. As pressure increases, volume decreases accordingly. After some compression, the first droplet of liquid will appear. That is, we have found the dew point of the mixture (point B). We then proceed with compression. As we further compress the system, more liquid will appear and the volume will continue to decrease.
It would appear that we are seeing here the same features as those of the single-component system that we studied in the previous modules. But wait a minute, is that so?
Actually, there is a difference. During the phase transition, pressure does not remain constant in this experiment. In fact, as compression progresses and more liquid is formed, pressure keeps rising — although not as sharply as in the single-phase vapor region. When the entire system has become liquid, with only an infinitesimal bubble of vapor left, we are at point C — the bubble point of the mixture. Please note that, for binary mixtures (as is the case for multicomponent mixtures,) the dew point and bubble point do not occur at the same pressure for isothermal compression. If you recall, for the single-component system, the dew point and the bubble point coincide. This is not true for binary and multicomponent systems. Compare Figure 4.2 with Figure 3.4 (repeated below from Module 3) to see this point.

WHY?? Why is pressure increasing during the phase transition? At this point, we start to realize the ways in which composition plays a fundamental role in the behavior of mixtures.
In a single-component system, both liquid and vapor in the two-phase region have the same composition (there is only one chemical substance within the system). Now, when a mixture exists in a two-phase condition, different molecules of different species are present and they can be either in a liquid or vapor state (two-phase condition). Some of them would “prefer” to be in the gas phase while the others would “prefer” to be in the liquid phase. This “preference” is controlled by the volatility of the given component. When we reach point B (Figure 4.2) and the first droplet of liquid appears, the heaviest molecules are the ones that preferentially go to that first tiny droplet of liquid phase. For ‘heavy’ molecules, given the choice, it is more desirable to be in the condensed state.
As we keep on forming more liquid (by compression), mainly light molecules remain in the vapor phase. However, at the end point of the transition (point C in Figure 4.2) we have forced all of them to go to the liquid state — they no longer have a choice. This enforcement requires greater pressure. If you compare a sample of liquid at dew point conditions (point B in Figure 4.2) to one taken in the middle of the transition, it is clear that the former would be richer in heavy components than the latter. The properties of the heaviest component would be most influential at the dew point (when the liquid first appears); while the properties of the lighter component would be most influential at the bubble point (when the last bubble is about to disappear.)
In the two-phase region, pressure increases as the system passes from the dew point to the bubble point. The composition of liquid and vapor is changing; but — watch out! — the overall composition is always the same! At the dew point, the composition of the vapor is equal to the overall composition of the system; however, the infinitesimal amount of liquid that is condensed is richer in the less volatile component. At the bubble point, the composition of the liquid is equal to that of the system, but the infinitesimal amount of vapor remaining at the bubble point is richer in the more volatile component than the system as a whole.
In general, when two different species are mixed, some of the behaviors of the individual species and their properties will change. Their usual behavior (as pure components) will be altered as a consequence of the new field of molecular interactions that has been created. While kept in a pure condition, molecules only interact with like molecules. On the other hand, in a mixture new interactions between dissimilar molecules occur.
Our next step, in order to continue this discussion in a coherent manner, is to draw the complete P-V diagram for this binary mixture by delineating the two-phase region. In the same way as we did previously, we delineate the two-phase region by drawing a complete family of isotherms in the P-V diagram. Figure 4.3 illustrates this.
Again, the line connecting all of the bubble and dew points will generate the bubble and dew point curve, both of which meet at the critical point. Notice that the critical point does not represent a maximum in the P-V diagram of a mixture. Also note that bubble point pressures and dew point pressures are no longer the same.
Again, the isotherms through the two-phase region are not horizontal but have a definite slope. This must have an implication. In fact, it does. What if we now want to plot the P-T diagram for this mixture? Will we have only a single line, where bubble and dew point curves lie on top of each other, as we had for a single-component system? Of course not. Instead of both curves being together, the bubble point curve will shift to the upper left (higher pressures) and dew point curve will shift to the lower right (lower pressures) — both of them meeting at the critical point. Figure 4.4 shows us a typical phase envelope for a mixture.
Notice the enormous difference between the P-T curve of a multi-component system (binary system in this case, Fig. 4.4) and the P-T curve of a pure (single) component (Fig. 3.1 of Module 3, repeated below). The only system for which the bubble point curve will coincide with the dew point curve is a single component system, where we have a single line for the P-T diagram (for example, the boiling point curve represented in Fig. 3.1). In Fig 3.1, the critical point represents the maximum set of (P,T) values that you could find in the P-T graph.
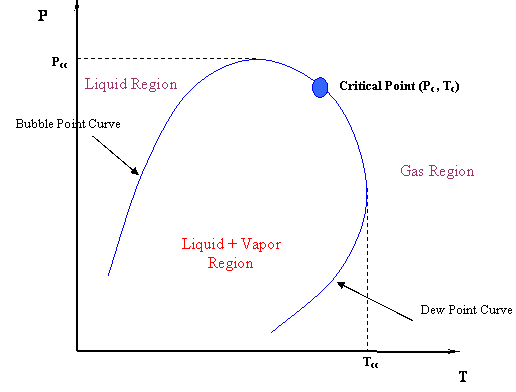
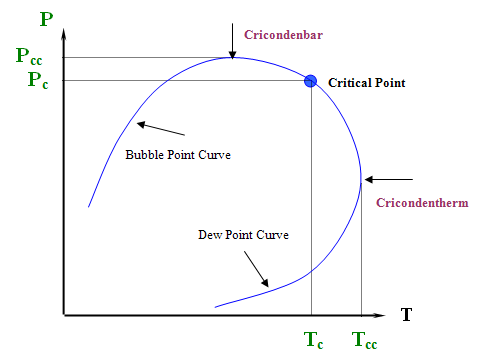
This is not all. There are some other implications. Can we say now that the critical point is the maximum value of pressure and temperature where liquid and gas can coexist? Look at Figure 4.4 again. Obviously not. The critical point is no longer at the apex or peak of the two-phase region; hence, vapor and liquid can coexist in equilibrium at T > Tc and P > Pc. In fact, we can identify two new maxima: condition Pcc is the maximum pressure and condition Tcc is the maximum temperature at which L+V will be found in equilibrium. We assign special names to these points. There are the cricondenbar and cricondentherm, respectively.
Clearly, the only definition that now can still hold for the critical point — both for mixtures and pure components — is the one shown below.
Critical Point (Pc,Tc): The temperature and pressure for which liquid and vapor are indistinguishable.
Again, this definition is applicable both for mixtures and pure-component systems; it does not make any reference to maximum values in the curve. These maximum values, as we said, have special names in the case of mixtures. Thus, for mixtures, we have to additionally define:
Cricondentherm (Tcc):
- The highest temperature in the two-phase envelope.
- For T > Tcc, liquid and vapor cannot co-exist at equilibrium, no matter what the pressure is.
Cricondenbar (Pcc):
- The highest pressure in the two-phase envelope.
- For P > Pcc, liquid and vapor cannot co-exist at equilibrium, no matter what the temperature is.
In the case of the unary system, besides dew and bubble point curves lying on top of each other, it is clear that cricondentherm, cricondenbar, and critical conditions are also represented by a single point (that is, the critical point itself.) This is clear from all three previous definitions. Thus, as we saw before, the definition for critical point in unary systems encompasses all three of the definitions given above.
For pure substances only:
Cricondentherm = Cricondenbar = Critical Point.
Retrograde Phenomenon
Regarding multi-component mixtures (where the binary system is the simplest case), some interesting phenomenon profoundly differentiate their behavior from the behavior of single-component systems. We are now talking about retrograde phenomena.
In the previous section, we learned how the “critical point” for a single-component system meant everything: the highest pressure and temperature at which two phases can exist and the point for which liquid and vapor phases are indistinguishable. Then we learned that this is not the case for multicomponent systems. Although the critical point for these systems is the common point between the dew and bubble point curves (the point for which liquid and vapor phases are indistinguishable), in general, this point neither represents the maximum pressure nor the maximum temperature for vapor-liquid coexistence. In fact, we gave new names to these maxima: cricondenbar (for the maximum pressure) and cricondentherm (for the maximum temperature). Let’s look at this again in Figure 4.5, where the critical point (Pc, Tc), cricondentherm (Tcc), and cricondenbar (Pcc) are highlighted.
Please recall that the bubble point curve represents the line of saturated liquid (100 % liquid with an infinitesimal amount of vapor) and the dew point curve represents the line of saturated vapor (100 % vapor with an infinitesimal amount of liquid). These conditions are all shown in Figure 4.5.
Let us now consider the isothermal processes taking place at T = T1 and T = T2, represented in Figure 4.6.
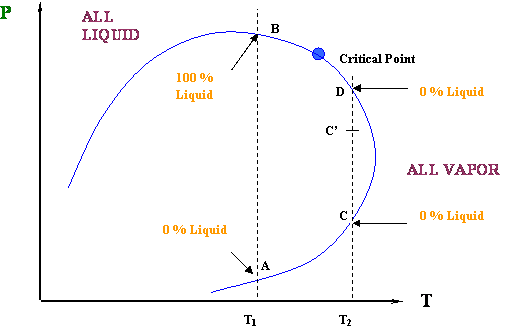
Figure 4.6 shows us two cases of isothermal compression for two different temperatures T1 and T2. Notice that these temperatures are such that T1 < Tc and Tc < T2 < Tcc.
It is common knowledge that an isothermal compression (increasing pressure while temperature is held constant) causes the condensation of a vapor (steam, in the case of water). That is the normal or expected behavior of a vapor under compression: the more you compress it, the more liquid you get out of it after the saturation conditions have been reached. This is always true for a pure-component system, such as water.
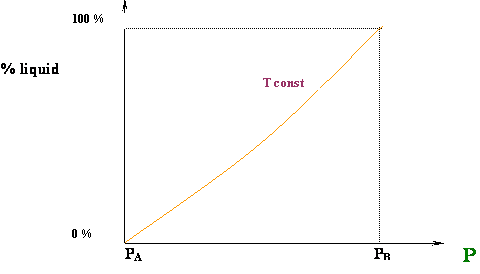
Well, that is exactly what is happening for our first case, the isothermal compression at T = T1. At point A, we are in an ALL VAPOR condition (0 % liquid) and we are starting to cross over into the two-phase region. As we compress from point A to B, more and more liquid is formed until the entire system has been condensed (point B). We went all the way from 0 % liquid to 100 % liquid, as we expected, by compressing the vapor. How liquid yield progresses with pressure is shown in Figure 4.7.
Again, there is nothing contrary to expectations here, and we would get the same result as long as T < Tc. However, there is something very interesting going on within the region Tc < T < Tcc.
In the second case (Tc < T2 < Tcc), we have a different behavior. At point C (Figure 4.6), we are starting in an ALL VAPOR condition (0 % liquid); by increasing pressure, we force the system to enter the two-phase region. Thus, some liquid has to drop out; we expect that as the pressure keeps increasing, we will produce more and more liquid. That is true to some extent… BUT, look at the final point of our journey, point D: although we are producing liquid, our final condition (dew point) requires us to have 0 % liquid in the system again.
How so?? This is telling us that, as we are entering the two-phase region, we will start to produce some liquid; but, there will be a point (of maximum liquid yield) where that liquid will start to vaporize (point C’). In other words, even though we are compressing the system, liquid will vaporize and not condense. Isn’t this contrary to expectations? Yes, and that is why we call this a retrograde (contrary to expectation) behavior.
Figure 4.8 shows a typical curve for the variation of the liquid volume percentage with pressure. This curve can be also referred to as the liquid dropout curve.
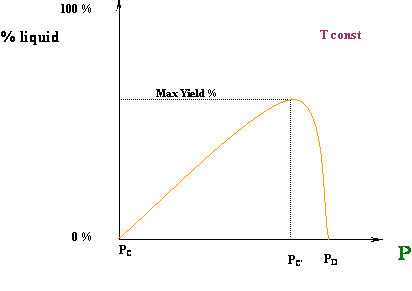
The increase in the liquid fraction with decreasing pressure between points C and D is exactly the opposite of the normal trend. This behavior, however, is typical of gas condensate systems. Retrograde conditions may be encountered in deep-well gas production, as well as in reservoir conditions.
For production operations, usually the objective is to maintain pressure so as to achieve maximum liquid dropout. The initial PVT conditions of the well may correspond to a point above point D. If the conditions at the wellhead are then maintained near point C’, liquid recovery is maximized at the surface. However, maximum liquid dropout is not always sought. At reservoir conditions, the presence of liquid is not desirable in a gas reservoir, because liquids have negligible mobility (at low saturations) and thus, the hydrocarbon would be — for practical purposes — lost forever. Liquid also impairs gas mobility; hence, liquid production at reservoir conditions is to be avoided at all times in a gas reservoir. This is often achieved by repressurization or lean gas injection.
It is also important to see that a similar behavior is to be expected within the region Pc < P < Pcc. In this case, we talk about retrograde vaporization since we will be moving from a 100 % liquid to another 100 % liquid condition (both on the bubble point curve) in an isobaric heating.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
Compare and contrast the definition of critical point for a single component system and a mixture. What is common between these two systems and what is not? Explain.
-
Do the cricondentherm and cricondenbar play a similar role as the critical point? If not, why? What is the difference?
- In a couple of sentences, speculate on the physics of why we have retrograde phenomena.
- Compare and contrast the 2-Phase segment of the P-v isotherm for single components and the P-v isotherm for a binary system. What is the difference?
Phase Diagrams, Part IV
Module Goals
Module Goal: To familiarize you with the basic concepts of Phase Diagrams as a means of representing thermodynamic data.
Module Objective: To familiarize you with the process of extracting quantitative compositional information from phase envelopes.
Effect of Composition on Phase Behavior
Let us try to reconcile the P-T graphs for the binary mixture with what we know from P-T graphs for single-component systems. At the end of the day, a mixture is formed by individual components which, when pure, act as presented in the P-T diagram shown in Fig. 3.1 [Module 3, repeated below]. We would, therefore, expect that the P-T diagram of each pure component will have some sort of influence on the P-T diagram of any mixture in which it is found.
In fact, it would be reasonable to think that as the presence of a given component A dominates over B, the P-T graph of that mixture (A+B) should get closer and closer to that of A as a pure component.
What this is telling us is that a new variable is coming into the picture: composition. So far we have not considered the ratio of component A to component B in the system. Now we are going to study how different ratios (compositions) will give different envelopes, i.e., different P-T behaviors.
Let us say that we have a mixture of components A (Methane, CH4) and B (Ethane, C2H6), where A is the more volatile of the two. It is clear that for the two pure components, we would have two boiling point curves for each component (A and B) as shown in Figure 5.1.
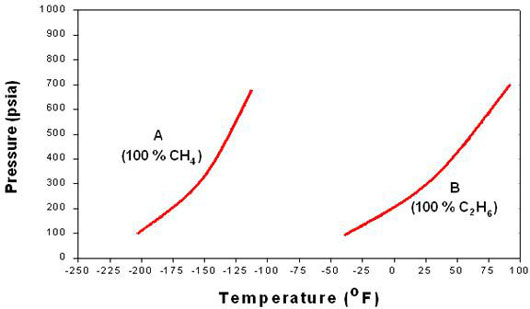
Please notice that the position of each of curve with respect to the other depends on its volatility. Since we are considering A to be the more volatile, it is expected to have higher vapor pressures at lower temperatures, thus, its curve is located towards the left. For B, the less volatile component, we have a boiling point curve with lower vapor pressures at higher temperatures. Hence, the boiling point curve of B is found towards the right at lower pressures.
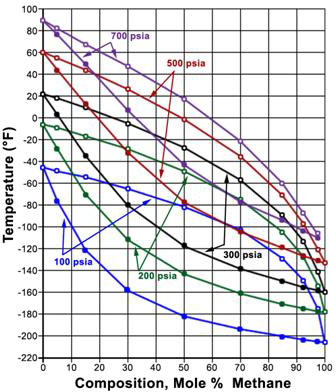
Now, if we mix A and B, the new phase envelope can be anywhere within curves A and B. This is shown in Figure 5.2, where the effect of composition on phase behavior of the binary mixture Methane/Ethane is illustrated.
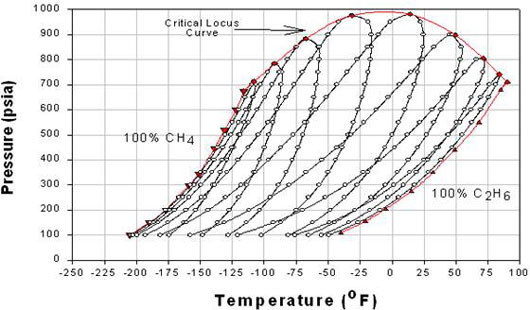
In Figure 5.2, each phase envelope represents a different composition or a particular composition between A and B (pure conditions). The phase envelopes are bounded by the pure-component vapor pressure curve for component A (Methane) on the left, that for component B (Ethane) on the right, and the critical locus (i.e., the curve connecting the critical points for the individual phase envelopes) on the top. Note that when one of the components is dominant, the curves are characteristic of relatively narrow-boiling systems, whereas the curves for which the components are present in comparable amounts constitute relatively wide-boiling systems.
Notice that the range of temperature of the critical point locus is bounded by the critical temperature of the pure components for binary mixtures. Therefore, no binary mixture has a critical temperature either below the lightest component’s critical temperature or above the heaviest component’s critical temperature. However, this is true only for critical temperatures; but not for critical pressures. A mixture’s critical pressure can be found to be higher than the critical pressures of both pure components — hence, we see a concave shape for the critical locus. In general, the more dissimilar the two substances, the farther the upward reach of the critical locus. When the substances making up the mixture are similar in molecular complexity, the shape of the critical locus flattens down.
Px and Tx Diagrams
In addition to considering variations with pressure, temperature, and volume, as we have done so far, it is also very constructive to consider variations with composition. Most literature on the subject calls these diagrams the “P-x” and “T-x” diagrams respectively. However, a word of caution is needed in order not to confuse the reader. Even though “x” stands for “composition” — in a general sense — here, we will see in the next section that it is also customary to use “x” to single out the composition of the liquid phase. In fact, when we are dealing with a mixture of liquid and vapor, it is customary to refer to the composition of the liquid phase as “xi” and use “yi” for the composition of the vapor phase. “xi” pertains to the amount of component in the liquid phase per mole of liquid phase, and “yi” pertains to the amount of component in the vapor phase per mole of vapor phase. However, when we talk about composition in general, we are really talking about the overall composition of the mixture, the one that identifies the amount of component per unit mole of mixture. It is more convenient to call this overall composition “zi”. If we do so, these series of diagram should be called “P-z” and “T-z” diagrams. This is a little awkward in terms of traditional usage; and hence, we call them “P-x” and “T-x” where “x” here refers to overall composition as opposed to liquid composition.
A P-x diagram for a binary system at constant temperature and a T-x diagram for a binary system at a constant pressure are displayed in Figures 5.3 and 5.4, respectively. The lines shown on the figures represent the bubble and dew point curves. Note that the end points represent the pure-component boiling points for substances A and B.
(Courtesy of ©LOMIC, INC)
In a P-x diagram (Figure 5.3), the bubble point and dew point curves bound the two-phase region at its top and its bottom, respectively. The single-phase liquid region is found at high pressures; the single-phase vapor region is found at low pressures. In the T-x diagram (Figure 5.4), this happens in the reverse order; vapor is found at high temperatures and liquid at low temperatures. Consequently, the bubble point and dew point curve are found at the bottom and the top of the two-phase region, respectively.
The Lever Rule
P-x and T-x diagrams are quite useful, in that information about the compositions and relative amounts of the two phases can be easily extracted. In fact, besides giving a qualitative picture of the phase behavior of fluid mixtures, phase diagrams can also give quantitative information pertaining to the amounts of each phase present, as well as the composition of each phase.
For the case of a binary mixture, this kind of information can be extracted from P-x or T-x diagrams. However, the difficulty of extracting such information increases with the number of components in the system.
At a given temperature or pressure in a T-x or P-x diagram (respectively), a horizontal line may be drawn through the two-phase region that will connect the composition of the liquid (xA) and vapor (yA) in equilibrium at such condition — that is, the bubble and dew points at the given temperature or pressure, respectively. If, at the given pressure and temperature, the overall composition of the system (zA) is found within these values (xA < zA < yA in the T-x diagram or yA < zA < xA in the P-x diagram), the system will be in a two-phase condition and the vapor fraction (αG) and liquid fraction (αL) can be determined by the lever rule:
(5.1a)
(5.1b)
Note that αL and αG are not independent of each other, since αL + αG = 1. Figure 5.5 illustrates how equations (5.1) can be realized graphically. This figure also helps us understand why these equations are called “the lever rule.” Sometimes it is also known as the “reverse arm rule,” because for the calculation of αL (liquid) you use the “arm” within the (yA-xA) segment closest to the vapor, and for the vapor calculation (αG) you use the “arm” closest to the liquid.
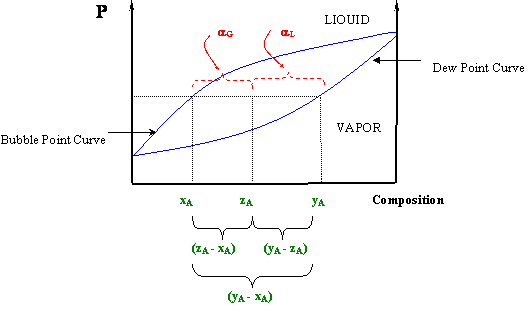
At this point you will see clearly why we needed to make a clear distinction among “xi” and “yi” and “zi”. Expressions (5.1) can be derived from a simple material balance. Can you prove it? [Hint: The number of moles of a component “i” per mole of mixture in the liquid phase is given by the product “xiαL”, while the number of moles of “i” per mole of mixture in the gas is given by “yiαG”. Since there are “zi” moles of component “i” per mole of mixture, the following must hold: . Can you proceed from here?]
Ternary Systems
The next more complex type of multi-component system is a ternary, or three-component, system. Ternary systems are more frequently encountered in practice than binary systems. For example, air is often approximated as being composed of nitrogen, oxygen, and argon, while dry natural gas can be rather crudely approximated as being composed of methane, nitrogen and carbon dioxide. We can also have pseudo 3-component systems, which consist of multicomponent systems (more than 3 components) that can be described by lumping all components into 3 groups, or pseudo-components. In this case, each group is treated as a single component. For example, in CO2 injection into an oil reservoir, CO2, C1, and C2 are often lumped into a single light pseudo-component, while C3 to C6 form the intermediate pseudo-component, and the others (C8+) are lumped together into a single heavy pseudo-component.
Intuitively, having more than two components poses a problem when a pictorial representation is desired. A rectangular coordinate plot, having only two axes, will no longer suffice. Gibbs first proposed the use of a triangular coordinate system. In modern times, we use an equilateral triangle for such a representation. Figure 5.6 shows an example of a ternary phase diagram. Note that the relationship among the concentrations of the components is more complex than that of binary systems.
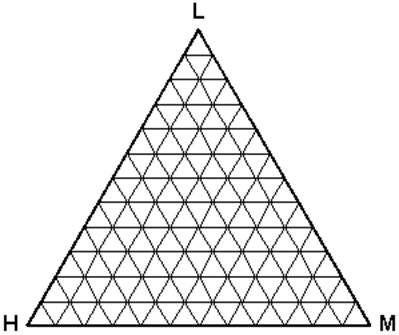
Features:
- Any point within this triangle represents the overall composition of a ternary system at a fixed temperature and pressure.
- By convention, the lightest component (L) is located at the apex or top of the triangle. The heavy (H) and medium (M) components are placed at the left hand corner and right hand corner, respectively.
- Every corner represents a pure condition. Hence, at the top we have 100 % L, and at each side, 100 % H and 100 % M, respectively.
- Each side of the triangle represents all possible binary combinations of the three components.
- On any of those sides, the fraction of the third component is zero (0%).
- As you move from one side (0 %) to the 100 % or pure condition, the composition of the given component is increasing gradually and proportionally. At the very center of the triangle, we find 33.33 % of each of the component.
To differentiate within the two-phase region and single-phase region in the ternary diagram, pressure and temperature must be fixed. There will be different envelopes (binodal curves) at different pressures and temperatures. The binodal curve is the boundary between the 2-phase condition and the single-phase condition. Inside the binodal curve or phase envelope, the two-phase condition prevails. If we follow the convention given above (lights at the top, heavies and mediums at the sides), the two-phase region will be found at the top. This can be seen more clearly in Figure 5.7.
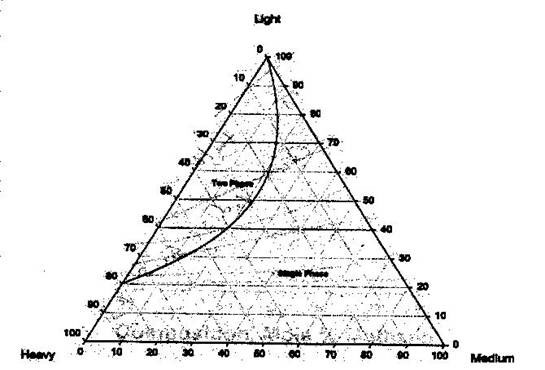
The binodal curve is formed of the bubble point curve and the dew point curve, both of which meet at the plait point. This is the point at which the liquid and vapor composition are identical (resembles the critical point that we studied before). Within the two-phase region, the tie lines are straight lines that connect the compositions of the vapor and liquid phase in equilibrium (bubble point to the dew point). These tie lines angle towards the medium-component corner. It can also be recognized that any mixture on a tie line has the same liquid and vapor compositions.
Finally, to find the proportion of liquid and vapor at any point on the tie line, we apply the lever rule.
Multicomponent Mixtures
For systems containing more than three components, pictorial representation becomes difficult, if not impossible. Simple diagrams can be obtained if the mole fractions of all but two or three components remain constant, and the variation of the two or three varying components with temperature and pressure are shown.
In practical applications, the mole fractions of all components can be expected to vary. For such systems, direct calculations based on physical models are the only way to obtain reliable information about the system phase behavior. This is the ultimate goal of this series of modules, and these calculations will be studied in detail as the course progresses.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
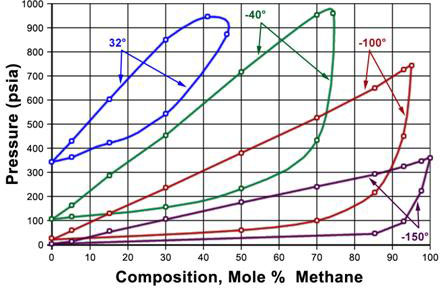
Figure 5.2 shows the P-T phase envelopes for eight binary mixtures of Methane and Ethane at eight different compositions. The data was experimentally generated at IGT (Institute of Gas Technology) and presented in the Research Bulletin No. 22. The vapor pressure curves of Methane and Ethane bound the phase envelopes of the eight binary mixtures of Methane and Ethane at different proportions. From left to right, these proportions (molar compositions) are:
P-T phase envelopes for eight binary mixtures of Methane and Ethane at eight different compositions Mixture Composition Mixture 1 97.50% CH4 and 2.50% C2H6 (closest to 100% pure Methane vapor pressure curve) Mixture 2 92.50% CH4 and 7.50% C2H6 Mixture 3 85.16% CH4 and 14.84% C2H6 Mixture 4 70.00% CH4 and 30.00% C2H6 Mixture 5 50.02% CH4 and 49.98% C2H6 Mixture 6 30.02% CH4 and 69.98% C2H6 Mixture 7 14.98% CH4 and 85.02% C2H6 Mixture 8 5.00% CH4 and 95.00% C2H6 (closest to 100% pure Ethane vapor pressure curve) Using this phase behavior data, generate the P-x and T-x diagram for Methane/Ethane mixtures at T = – 40 F and P = 500 psia respectively.
- If a certain amount of the mixture 40% C1 – 60% C2 is kept in a vessel at 500 psia, determine the temperature at which the vessel has to be subjected if at least 50% of the substance is required to be in the liquid state. How would your answer change if we were now required to have 10% of liquid in the vessel? How would it change if the overall composition is now considered to be 60% C1 and 40% C2 ?
- 10 lbmol of an equimolar C1/C2 mixture is confined inside a vessel at conditions of – 60oF and 500 psia. What is the percentage of liquid inside the vessel? What is the composition of the liquid and vapor at such condition?
- What would be the composition of the first bubble that appears in a isothermal expansion of a liquid at – 40oF? At which pressure would this bubble appear? What would be the pressure at which the first droplet appears in a isothermal compression of a vapor at – 40oF? What is the composition of such a droplet?
- Can you apply the lever rule to in a ternary diagram? If not, why not? What about a multicomponent system?
PT Behavior and Equations of State (EOS), Part I
Module Goals
Module Goal: To introduce you to quantification in fluid phase behavior.
Module Objective: To quantitatively and qualitatively compare ideal and real gas behavior.
Introduction
The ultimate purpose of this course is to build a firm knowledge of the phase behavior of fluids. With this understanding, we will be able to establish the basis and rationale upon which phase behavior applications in production systems are grounded. We are using the word production in a generic sense, that is, where it pertains to reservoir, pipeline, and the surface production (of any produced fluid).
So far, we have seen that much of the importance that we place on understanding phase behavior comes from the ability that it gives us to predict how a given system will behave at different conditions. We need phase diagrams to look at what the state of the system that we are dealing with is; that is, what is its original state. As a matter of fact, if we look at petroleum production, we often talk about a thermodynamic process that is taking place, involving a process path similar to one that we have seen in any basic thermodynamics course.
Just to give an illustration, consider Figure 6.1.

Production, as defined above, involves taking the reservoir from an initial condition (PA , Tf) to final state of depletion (PB , Tf), (PD , Tf), (PE , Tf) or even (PF , Tf). Once the end points of our thermodynamic path are fixed, the single most important question is determining the path that leads to such an end point. This path dictates whether or not you have the maximum recovery possible from the system.
When we talk about gas cycling, we are generally referring to the practice of injecting gas back into the reservoir. This is done in order to optimize the thermodynamic path we have chosen to take. In a typical condensate system, you generally produce a wet gas from the system with a high liquid yield at the surface. At the surface, you pass this gas through a series of separators; during this process liquid is going to drop out. The liquid that drops out will be rich in the heavier components. Hence, the gas that comes out of the separator will be dry (i.e., very light). If you inject this lean gas back into the reservoir, there will be a leaching process. All you are trying to do from the point of view of the phase diagram is to move the phase boundary and dew point towards the left (lower temperatures zones). Let me explain this in more detail.
Let us say that we have the phase envelope for the reservoir fluid shown in Figure 6.1, with the given path of production. If we were to follow the path from (A , Tf) to (E , Tf), we would enter the two-phase region and end up having liquid in the reservoir. However, you do not want liquid in the reservoir because its low mobility dictates that it would not be recovered! Next, you want to move that phase diagram to the left by injecting a lighter gas. When you inject a lighter gas, the phase envelope shifts to the left; your production path will be free of liquid dropout at reservoir conditions. By injecting the gas, we are making the overall composition of the reservoir fluid lighter. The effect of composition on phase behavior was discussed in the previous module (see Figure 5.2 in Module 5). This example demonstrates the importance of phase diagrams as tools that help us produce a reservoir in an optimal way.
So, we recognize that we needed phase behavior data for this particular system. The question now is how do we get the data? We can collect data in at least two ways: from laboratory measurements and from field measurements. Lab experiments are expensive, and we cannot hope to generate data for every foreseeable condition we may encounter. Just to give you an idea, generating a single phase envelope may cost at least $120,000. This is not something you want to be doing all the time. On the other hand, if you went to the field, you would lose valuable resources or have to stop operations to make your observations. On a routine basis, you don’t want to use the field or a lab as your main sources of phase behavior data. These options mean a lot of lost revenue and a great deal of expense. Is there a third option? Yes, indeed. We can rely on prediction, by which we produce a model that can do this work for us. In fact, we will be dealing with, and developing, this option in this course.
The basis for such a model is what is called an Equation of State (EOS). Hence, the central part of this course is EOS, since they are the basis of what we do in phase behavior.
There are several other examples that illustrate very vividly why we need to study equations of state. For instance, let us think about the concept of equilibrium.
In petroleum production, we generally make the assumption that, at every stage, the system is in equilibrium. When you think about equilibrium, you generally think about a system that is static, that is, not moving. When a system is moving, it cannot, in actuality, be in equilibrium. Nevertheless, the best approach we have so far is to describe it using equilibrium thermodynamics. While we usually assume equilibrium, we recognize that it is not a perfect assumption, but that it is a reasonable one.
This means that in the course of producing the reservoir, a process which always involves movement, I am assuming that everywhere the gas and the liquid are in equilibrium. With this assumption, we are free to use equilibrium thermodynamics, so we are able to employ EOS in describing the state of the system.
Consider the reservoir in Figure 6.1, in an entirely gaseous condition at (A, Tf), and having a known fluid composition zri (i=1,…n). As we produce this reservoir through a pipeline, we take the fluid from reservoir conditions through a battery of separators. Generally speaking, we deal with a series of separators, but for the sake of this discussion we will assume that we have just a single separator.
This separator does not care about the pressure and temperature of the reservoir. It only cares about its own pressure and temperature condition: Ps, Ts. The composition of the fluid at the separator inlet is assumed to be the same as that of the reservoir fluid, although this is strictly true only for single phase conditions.
The fluid exits the separator in two streams: a vapor stream and a liquid stream. As a petroleum engineer, we want to know how much gas, how much liquid, and the quality (compositions) of both streams. That is, we need quantitative and qualitative information. As we shall study in Module 12, we can perform a material balance around each separator to calculate the amount of vapor and liquid that is to be recovered. We will need the properties of both streams (such as density and molecular weight) in order to express flow rates in suitable field units.
How do we generate all this? We need a tool; that tool is an Equation of State! Why do we need an Equation of State? We need EOS to define the state of the system and to determine the properties of the system at that state. That is why it is called an equation of state. As you may have noticed, something critical in this series of lectures is the ability to establish links within all the material we are studying. We will not look at each topic simply as an isolated compartment, but instead, we must think in terms of how each piece of information fits into the overall picture that we are developing.
P-V-T Behavior
We embark now on a rather ambitious journey. Given a fluid, we would like to develop mathematical relationships for predicting its behavior under any imaginable condition of pressure, temperature and volume (P-V-T). In other words, we want to describe the P-V-T behavior of fluids in general.
As we stated earlier, this is a very challenging problem. The way science approaches these sorts of problems is to introduce simplifications of the physical reality. In other words, we formulate a set of assumptions and come up with a base model that we might call ideal. From that point on, once the base model has been established, we look at a real case by estimating how close (or far) it performs, with respect to the base (ideal) case, and introducing the corresponding corrections. Such corrections will take into account all the considerations that our original assumptions left out.
Let us discuss our base case for fluids (the simplest fluid we may deal with): the ideal or perfect gas.
Ideal Behavior
An ideal gas is an imaginary gas that satisfies the following conditions:
- Negligible interactions between the molecules,
- Its molecules occupy no volume (negligible molecular volume),
- Collisions between molecules are perfectly elastic — this is, no energy is lost after colliding.
We recognize that this fluid is imaginary because — strictly speaking — there are no ideal gases. In any fluid, all molecules are attracted to one another to some extent. However, the ideal approximation works best at some limiting conditions, where attraction forces can be considered to be weak. In fact, ideal behavior may be approached by real gases at low pressures (close to atmospheric) and high temperatures. Note that at low pressures and high temperatures, the distance between any pair of gas molecules is great. Since attraction forces weaken with distance, we have chosen a condition where attraction forces may be neglected. In conclusion, we consider a gas ideal when each molecule behaves as if it were alone — molecules are so far apart from each other that they are not affected by the existence of other molecules.
The behavior of ideal gases has been studied exhaustively and can been extensively described by mathematical relationships.
For a given mass of an ideal gas, volume is inversely proportional to pressure at constant temperature, i.e.,
(6.1)
This relationship is known as Boyle’s Law. Additionally, volume is directly proportional to temperature if pressure is kept constant, i.e.,
(6.2)
This relationship is known as Charles’ Law. By combining both laws and recognizing “R” (the universal gas constant) as the constant of proportionality, we end up with the very familiar equation:
< (6.3)
This represents the equation of state (EOS) of an ideal gas. Numerical values of “R” depend on the system of units that is used:
If we construct the P-v diagram for an ideal gas at a given temperature, we end up with the isotherm shown in Figure 6.2.
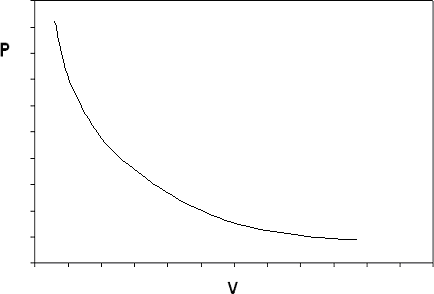
The ideal gas model predicts two limiting fluid behaviors: first, that the volume of the gas becomes very large at very low pressures as , a concept that agrees with what we know from our experience in the physical world). And second, as (the volume of matter just “vanishes” if the pressure is high enough: this concept we would not be as willing to accept). These two behaviors are a consequence of the assumptions made in the ideal gas model.
Real Gases
In reality, no gas behaves ideally. Therefore, the ideal EOS is not useful for practical applications, although it is important as the basis of our understanding of gas behavior. Even though the ideal model is not reliable for real engineering applications, we have to keep in mind that the ideal gas EOS is the starting point of all modern approaches.
If we look back at Figure 6.2 and recall our discussions about P-v behavior of pure substances, something should catch your attention. Figure 6.3 shows us the typical P-v behavior of a pure substance to facilitate our discussion.
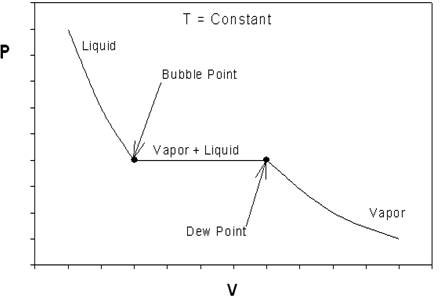
What can we conclude about the ideal EOS while contrasting Figure 6.2 to 6.3? The curve in Figure 6.2 is continuous; Figure 6.3 has an obvious discontinuity (at the vapor+liquid transition). Hence, one thing we can already say is that the ideal EOS is at least qualitatively wrong. For a real substance, as pressure increases, there must be a point of discontinuity that represents the phase change. Ideal gas will not condense, no matter what pressure it is subjected to, regardless of the temperature of the system. In other words, we cannot hope to reproduce the P-v behavior of Figure 6.3 using the ideal equation (6.3) since no discontinuity is to be found. However, the real P-v isotherm can be approximated by ideal behavior at low pressures, as we can see from the plots.
We can also establish some quantitative differences between ideal and real PVT behavior. For example, for most conditions of interest at a given volume and temperature, the ideal gas model over-predicts the pressure of the system:
(6.4)
We can explain this difference by recalling that a real gas does have interaction forces between molecules. Secondly, we recall that the concept of “pressure” of a gas is a consequence of the number of molecular collisions per unit area against the wall of the container. Such number of collisions is, in turn, a measure of the freedom of the molecules to travel within the gas. The ideal gas is a state of complete molecular freedom where molecules do not even know the existence of the others. Hence, a hypothetical ideal gas will exert a higher pressure than a real gas at any given volume and temperature. When molecules come together (real gas), it reduces the available free space for the molecules and pressure is reduced.
Additionally, the ideal model assumes that the physical space that the molecules themselves occupy is negligible. In reality molecules are physical particles and they do occupy space. Once we find a way of accounting for the space that the molecules themselves occupy, we would be able to compute a “real” free volume available for the molecules to travel through the gas. In the ideal case, this free volume is equal to the volume of the container itself since molecular volume is not accounted for. In the real case, this free volume must be less than the volume of the container itself after we account for the physical space that molecules occupy. Therefore:
(6.5a)
(6.5b)
Summary
The ideal gas EOS is inaccurate both quantitatively and qualitatively. Quantitatively, ideal gas will not condense no matter what pressure and temperature the system is subjected to. Quantitatively, pressures and volumes used by the ideal gas model are higher than the values that a real gas would have. These are the primary reasons that scientists have made an effort to go beyond the ideal gas EOS, simply because it does not apply for all the cases of interest.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
Under what conditions should a real gas behave as an ideal gas?
-
Can we manufacture an ideal gas?
- Write a paragraph on what you think we should do with the ideal gas equation to make it applicable to real gases. Describe all the considerations that you feel must be accounted for.
PT Behavior and Equations of State (EOS), Part II
Module Goals
Module Goal: To introduce you to quantification in fluid phase behavior.
Module Objective: To introduce you to the concept of Z-factor and the van der Waals equation of state.
Z-Factor
From the last module, it is very likely that one question is left in our minds. How can we adjust the ideal model to make it suitable for real gases? Well, we already have the answer. We said that once we have established a base (ideal) model, we look at a real case by estimating how close (or far) it performs with respect to the base (ideal) case, and introducing the corresponding corrections. Again, such corrections will take into account all the considerations that our original assumptions left out.
For the case of gas behavior, we introduce a correction factor to account for the discrepancies between experimental observations and predictions from our ideal model. This correction factor is usually referred to as the compressibility factor (Z), and is defined as:
(7.1)
In the previous equation, V is the real volume occupied by the gas and VIdeal is the volume that the ideal model predicts for the same conditions. The ideal volume is given by:
(7.2)
Hence, the equation of state for real gases is written as:
(7.3)
Engineers are very much familiar with this equation, to the extent that it is usually recognized as Engineering EOS. Please note that for Z = 1, this equation collapses to the ideal gas model. In fact, unity is the compressibility factor of any gas that behaves ideally. However, please note that Z = 1 is a consequence of ideal behavior, but this is not a definition.
Something to think about:
Is it possible to have a real gas at a condition at which Z=1 without being ideal (far removed from the ideal-gas theory assumptions)?
For natural gases, the most enduring method of estimating Z has been the Katz-Standing Method. However, we are now living in a computer-driven era, where thermodynamic estimations are very rarely taken from graphs or plots, as was common in the past.
Definition of Equation of State (EOS)
Assuming an equilibrium state, the three properties needed to completely define the state of a system are pressure (P), volume (V), and temperature (T). Hence, we should be able to formulate an equation relating these 3 variables, of the form f(P,T,V)=0.
An equation of state (EOS) is a functional relationship between state variables — usually a complete set of such variables. Most EOS are written to express functional relationships between P, T and V. It is also true that most EOS are still empirical or semi-empirical. Hence, the definition:
An Equation of State (EOS) is a semi-empirical functional relationship between pressure, volume and temperature of a pure substance. We can also apply an EOS to a mixture by invoking appropriate mixing rules.
There have been a number of attempts to derive a theoretically sound EOS; but, generally speaking, not much success has been achieved along that line. As a result, we use what are known as semi-empirical EOS. Most equations of state used today are semi-empirical in nature, this being so because they are fitted to data that are available. Additionally, equations of state are generally developed for pure substances. Their application to mixtures requires an additional variable (composition) and hence an appropriate mixing rule.
The functional form of an EOS can be expressed as:
(7.4)
where ak = EOS parameters.
As we stated earlier, most applicable EOS today are semi-empirical, in the sense that they have some theoretical basis but their parameters (ak) must be adjusted. The number of parameters (np) determines the category/complexity of the EOS. For instance, 1-parameter EOS are those for which np = 1, and 2-parameter EOS are those for which np = 2. The higher “np” is, the more complex is the EOS. Also, in general terms, the more complex the EOS, the more accurate it is. However, this is not always the case; in some cases a rather simple EOS can do a very good job.
Since the time of the ideal gas law (ideal gas EOS), a great number of equations of state have been proposed to describe real gas behavior. However, many of those have not passed the test of time. Only few have persisted through the years, this because of their relative simplicity. In the petroleum business, the most common modern EOS are the Peng Robinson EOS (PR EOS) and Soave-Redlich-Kwong EOS (SRK EOS). Both of these are cubic EOS and hence derivations of the van der Waals EOS, which we will be discussing next. There are other more complex EOS, although they have not yet found widespread application in our field:
- Lee Kesler EOS (LK EOS)
- Benedict-Webb-Rubin EOS (BWR EOS)
- Benedict-Webb-Rubin-Starling EOS (BWRS EOS)
In the natural gas business, especially in the gas transmission industry, the standard EOS used is the AGA EOS; this is an ultra-accurate EOS for Z-factor calculations — a very sensitive variable for custody-transfer operations.
Purpose and Historical Development
We want to use EOS as the basis for generating data: volumetric data, thermophysical data, and to help us perform vapor/liquid equilibrium (VLE) calculations. Probably there has not been an area of thermodynamics to which so many hours of research have been devoted as that of the topic of EOS. Among the properties derived from an EOS include:
- Densities (vapor and liquid),
- Vapor pressures of pure components,
- Critical pressures and temperatures for the mixture,
- Vapor-Liquid equilibrium (VLE) information,
- Thermodynamic properties .
300 years of EOS Development
PERIOD 1: “Foundational work”
Before 1662, there was an incomplete understanding and qualitative representation of the volumetric behavior of gases.
1662: First breakthrough — Boyle’s Law. Boyle did not define an ideal behavior. When he proposed this law, he was convinced that it applied to all gases. Among the limitations that Boyle was working under: no high pressure measurements could have been taken using the equipment of his time, and his working fluid was air. Hence, it is no wonder that everything these pioneers did pertained to what we now recognize as the ideal state.
PV = constant
1787: Charles’ Law. It was one hundred plus years until a new, important development in the gas behavior field. Charles postulated that the volume of a gas is proportional to its temperature at isobaric conditions.
Combining, PV/T = constant = R, gas constant
1801: Dalton introduced the concept of partial pressures and recognized that the total pressure of a gas is the sum of the individual (partial) contributions of its constituents.
1802: Gay-Lussac. He helped to define the universal gas constant “R”. Dalton had looked at different gases and calculated the ratio PV/T to verify that it was constant. However, it was believed that each gas may have its own R. Gay-Lussac showed that a single constant applied to all gases, and calculated the “universal” gas constant.
1822: Cagniard de la Tour. He discovered the critical state (critical point) of a substance.
1834: Clapeyron. He was the first to suggest PV=R(T+273).
PERIOD 2: “Monumental Work”
Period of turning points and landmarks with quantitative developments.
1873: van der Waals. With van der Waals, a quantitative approach was taken
for the first time. He was an experimentalist and proposed the continuity of gases and liquid that won for him a Nobel Prize. He has provided the most important contribution to EOS development.
1875: Gibbs, an American mathematical physicist, made the most important contributions to the thermodynamics of equilibrium in what has been recognized as a monumental work.
1901: Onnes theoretically confirmed the critical state.
1902: Lewis defined the concept of fugacity.
1927: Ursell proposed a series solution (polynomial functional form) for EOS: P = 1 + b/V + c/V2 + d/V3 +… This is known as the virial EOS. Virial EOS has better theoretical foundation than any other. However, cubic EOS (as vdW’s) need only 2 parameters and have become more widespread in use.
PERIOD 3: “Incremental Improvement”
During this last and current period, a better quantitative description of volumetric behavior has been achieved at a rather low pace. What is striking, as we will study later, is that most of the tools of most critical use for us today are based on the works of van der Waals, Gibbs, and Lewis, and have been around for years.
1940: Benedit, Webb, & Rubbin proposed what can be called the “Cadillac” of EOS, i.e., the most sophisticated and most accurate for some systems. However, the price to pay is that it is complicated and not easy to use.
1949: Redlich & Kwong introduced a temperature dependency to the attraction parameter “a” of the vdW EOS.
1955: Pitzer introduced the idea of the “acentric factor” to quantify the non-sphericity of molecules and was able to relate it to vapor pressure data.
1972: Soave modified the RK EOS by introducing Pitzer’s acentric factor.
1976: Peng and Robinson proposed their EOS as a result of a study sponsored by the Canadian Gas Commission, in which the main goal was finding the EOS best applicable to natural gas systems.
Since then, there has not been any radical improvement to SRK and PR EOS, although a great deal of work is still underway.
The van der Waals Equation
Even though van der Waals EOS (vdW EOS) has been around for more than one hundred years, we still recognize van der Waals’ achievements as crucial in revolutionizing our thinking about EOS. We talk about vdW EOS because of pedagogical reasons, not because it finds any practical application in today’s world. In fact, vdW EOS is not used for any practical design purposes. However, most of the EOS being used widely today for practical design purposes have been derived from vdW EOS.
The contributions of vdW EOS can be summarized as follows:
- It radically improved predictive capability over ideal gas EOS,
- It was the first to predict continuity of matter between gas and liquid,
- It formulated the Principle of Corresponding States (PCS),
- It laid foundations for modern cubic EOS.
In his PhD thesis in 1873, van der Waals proposed to semi-empirically remove the main key “weaknesses” that the ideal EOS carried with it. Essentially, what he did was to look again at the basic assumptions that underlie the ideal EOS, which we have listed above.
vdW accounted for the non-zero molecular volume and non-zero force of attraction of a real substance. He realized that there is a point at which the volume occupied by the molecules cannot be neglected. One of the first things vdW recognized is that molecules must have a finite volume, and that volume must be subtracted from the volume of the container. At the same time, he modified the pressure term to acknowledge the fact that molecules do interact with each other though cohesive forces. These are the two main valuable recognitions that he introduced.
The ideal EOS states:
(7.5)
or,
(7.6)
where of the substance.
vdW focused his attention on modifying the terms “P” and “v” in the original ideal gas law by introducing an appropriate correction. Looking back at the inequality of equation (6.4) in Module 6, vdW proposed that the difference of both pressures is the result of the attraction forces — cohesive forces — neglected in the ideal model (equation 7.6) and thus,
(7.7)
At this point, vdW postulated the term Pattraction, an inverse function of the mean distance between molecules — this being a direct consequence of Newton’s law of inertial attraction forces, F (distance)-2. Recognizing that the volume of the gas is a measure of the mean distance between molecules (the smaller the volume, the closer the molecules and vice versa),
(7.8)
and using “a” as a constant of proportionality,
(7.9)
Next, vdW took care of the inequality in equation (6.5) (see Module 6). Any particle occupies a physical space; hence, the space available to the gas is less than the total volume of its container. Let us say we can experimentally determine the actual physical space that all the molecules in the container occupy, and that we call it “b”, or the co-volume. vdW then proposed:
(7.10)
The inclusion of a parameter “b” (co-volume) recognizes the role of repulsive forces. Repulsive forces prevent molecules from “destroying” one another by not letting them get too close. In a condensed state, there is a maximum allowable “closeness” among molecules. Therefore, it is because of repulsive forces that we cannot compress the volume of a fluid beyond its co-volume value “b”. If the molecules get too close to each other, repulsion forces take over to prevent their self-destruction.
In summary, vdW proposed to correct the pressure and volume terms of the ideal model represented by equation (7.6). The “new” modified-ideal equation of state becomes:
(7.11a)
or,
(7.11b)
where:
P = absolute pressure
v = molar volume
T = absolute temperature
R = universal gas constant
Equation (7.11b) demonstrates that vdW EOS is explicit in pressure. At this stage it is important to stress that any prediction for from equations (7.11) is meaningless due to the physical significance that we have attached to this parameter. Since all the others parameters are constants, equations (7.11) are functional relationships of the variables P, T and :
(7.12)
Therefore, equation (7.11a) expresses a PVT relationship and hence, it is an equation of state. In this equation, “a” and “b” are constants that are specific to each component. However, the numerical value of “R” depends on the system of units chosen, as we discussed above.
It is time to ask ourselves a very important question:
How do we calculate “a” and “b” for each substance?
As can be inferred from their definitions, “a” and “b” are different for different substances; i.e.,
How do we relate “a” and “b” to well-known and easily-obtainable physical properties of substances?
It turns out that there are a set of conditions called criticality conditions that must be satisfied for all systems, provided that those systems satisfy the 2nd law of thermodynamics. Indeed, in the previous chapter we recognized that the critical isotherm of a pure substance has a point of inflexion (change of curvature) at the critical point. Furthermore, we recognized the critical point to be the maximum point (apex) of the P-V envelope. This condition of horizontal inflexion of the critical isotherm at the critical point is mathematically imposed by the expression:
(7.13)
These conditions are called the criticality conditions. It turns out that when one imposes these conditions on equation (7.11a), one is able to derive expressions for the parameters “a” and “b” as a function of critical properties as follows:
(7.14a)
(7.14b)
You may want to prove this as an exercise. “a” and “b” can therefore be known because they are functions of known (tabulated) properties of all substances of interest (critical pressure and temperature.)
So far, we have applied vdW EOS to pure components. Can we extrapolate this to apply to multi-component systems?
To extend this concept to a system of more than one component, we use what is called a mixing rule. A mixing rule relates the parameters that characterize the mixture (am and bm) to the individual contributions of the pure components that make up that mixture (ai and bi)
How do we do this? vdW proposed to weight the contributions of each component using their mole compositions, as follows:
(7.15a)
(7.15b)
The former is called the quadratic mixing rule, while the latter is known as the linear mixing rule.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
If a gas is ideal, would its compressibility factor (Z) be always equal to one?
-
For a gas with Z=1, would its behavior be ideal?
- Take a look at the Standing-Katz Compressibility Factor Plot for Natural Gases. What is the information you need to obtain a value of “Z” for a gas? What happens to “Z” at low pressures? What is the behavior of “Z” at high pressures? What is the compressibility factor of Methane (Pc = 666 psia, Tc = – 117 F) at P = 1000 psia and T = 0 F?
- As pressure approaches to zero, what should vdW EOS collapse to? Why? Can you show it?
- Speculate on how you could calculate the “Z” factor for a gas using vdW EOS.
PT Behavior and Equations of State (EOS), Part III
Module Goals
Module Goal: To introduce you to quantification in fluid phase behavior.
Module Objective: To highlight the principle of corresponding states and its importance for thermodynamic correlations.
Principle of Corresponding States (PCS)
The principle of Corresponding States (PCS) was stated by van der Waals and reads: “Substances behave alike at the same reduced states. Substances at same reduced states are at corresponding states.” That is,
“Substances at corresponding states behave alike.”
Reduced properties are used to define corresponding states. Reduced properties provide a measure of the “departure” of the conditions of the substance from its own critical conditions and are defined as follows:
(8.1a)
(8.1b)
(8.1c)
If Pr = Tr = vr = 1, the substance is at its critical condition. If we are beyond critical conditions, Tr > 1, Pr > 1 and vr > 1. By the same token, if all the conditions are subcritical, Tr < 1, Pr < 1 and vr < 1. Critical conditions become the scaling factor by which substances can be compared among each other in terms of their “departure from criticality” or reduced properties.
The PCS says that all gases behave alike at the same reduced conditions. That is, if two gases have the same “relative departure” from criticality (i.e., they are at the same reduced conditions), the corresponding state principle demands that they behave alike. In this case, the two conditions “correspond” to one another, and we are to expect those gases to have the same properties.
The Corresponding State Principle can be derived from vdW EOS. If we recall,
(8.2a)
where:
(8.2b)
(8.2c)
We defined the reduced conditions as:
(8.3)
If we substitute all this into vdW EOS,
(8.4)
Simplifying the expression, and employing the expressions:
(8.5a)
(8.5b)
We get:
(8.6)
Equation (8.6) is the reduced form of vdW EOS. See how this equation is “universal”. It does not care about which fluids we are talking about. Just give it the reduced conditions “Pr, Tr” and it will give you back vr — regardless of the fluid. Hence, if you compute vr for a certain fluid by entering Pr and Tr for that fluid into vdW reduced EOS (equation 8.6), you will compute the same vr, for any other fluid at the same conditions of Pr and Tr. There is no other possibility. Strictly speaking, van der Waals’ Corresponding States Principle reads: “fluids at the same reduced pressures and temperatures have the same reduced volume.” This is how van der Waals discovered the Principle of Corresponding States. As long as two gases are at corresponding states (same reduced conditions), it does not matter what components you are talking about, or what is the nature of the substances you are talking about; they will behave alike.
The critical point provides the perfect scaling for the application of the corresponding state principle because of the existence of the criticality conditions. In fact, equation (7.13) [Module 7] makes the application of corresponding states possible for equations of state.
(7.13)
Indeed, for us to arrive at equation (8.6), we needed to use equations (8.2) — which in turn were the outcome of the application of the criticality conditions to van der Waals’ equation of state. As a result, gases that have the same relative departure from their own critical condition have the same properties.
What is the use of this principle? Basically, it is used for thermodynamic correlations — its most powerful application. Most thermodynamic correlations have been made viable and general because of the application of the principle of corresponding states. An excellent example is the popular Z-chart of Standing and Katz, shown in Figure 8.1. In fact, most of the correlations that we use in thermodynamics are based on this principle. This explains why “Pr” and “Tr” so often appear in thermodynamic correlations. The main reason for using “Pr” and “Tr” is to obtain the most generalized correlation possible, so that it is suitable for use with most substances.
(Reference: Standing and Katz, Trans. AIME, 1942)
Acentric Factor and Corresponding States
It is important to point out that the PCS that we have just discussed was originally outlined by van der Waals. In reality, it is the simplest version of the principle of corresponding states, and it is referred to as the two-parameter PCS. This is because it relies on two parameters (reduced pressure and temperature) for defining a “corresponding state.”
With the passing of time, more accurate PCS formulations have made use of more than two parameters. For instance, the three-parameter PCS affirms that two substances are in corresponding states not only when they are at the same reduced conditions (reduced pressure and temperature), but also when they have the same “acentric factor” value. In any case, the general statement of PCS remains untouched:
“Substances at corresponding states behave alike.”
What makes the difference is the definition of “what a corresponding state is.”
The acentric factor “w” is a concept that was introduced by Pitzer in 1955, and has proven to be very useful in the characterization of substances. It has become a standard for the proper characterization of any single pure component, along with other common properties, such as molecular weight, critical temperature, critical pressure, and critical volume.
Pitzer came up with this factor by analyzing the vapor pressure curves of various pure substances. From thermodynamic considerations, the vapor pressure curve that we studied in our first modules for pure components can be mathematically described by the Clausius Clapeyron equation:
(8.7)
The use of the integrated version of equation (8.7) is very common for the mathematical fitting of vapor pressure data. The integrated version of equation (8.7) shows that the relationship between the logarithm of vapor pressure and the reciprocal of absolute temperature is approximately linear. That is, in terms of reduced conditions, vapor pressure data approximately follows a straight line when plotted in terms of “logPr” versus “1/Tr”, or, equivalently:
(8.8)
If the two-parameter corresponding state principle were to hold true for all substances, the parameters “a” and “b” should be the same for all substances. That is, all vapor pressure curves of all imaginable substances should lie on top of each when plotted in terms of reduced conditions. Stated in another way, if the plot is of the form “logPr” versus “1/Tr”, all lines should show the same slope (a) and intercept (b).
The bad news is that, as you may imagine, this is not always true. Vapor pressure data for different substances do follow different trends. The good news is that some gases follow the expected trend. Which are they? The noble gases. Noble gases (such as Ar, Kr and Xe) happen to follow the two-parameter corresponding states theory very closely. Hence, they yield themselves amenable to acting as a reference to evaluate “compliance” with the two-parameter equation of state.
Pitzer wanted to come up with a reliable way of quantifying the deviation of substances with respect to two-parameter corresponding state predictions. He decided to use noble gases as the base for comparison. Analyzing vapor pressure data for noble gases, Pitzer showed that a value of logPr = – 1 was achieved at approximately Tr = 0.7. So, BINGO! There you are! He thought: if the vapor pressure data of a substance show that logPr = – 1 at Tr = 0.7, it behaves as the noble gases and thus complies with the two-parameter corresponding states. If not, we are to compute the difference:
(8.9)
Pitzer called this difference the “acentric factor, ” of the substance. Noble gases, being the reference themselves, have an acentric factor value of zero (=0). Substances with an acentric factor of zero are called “simple” substances. The acentric factor is said to be a measure of the non-sphericity (acentricity) of the molecules. Therefore, the three-parameter corresponding state theory of Pitzer reads: “Fluids that have the same value of will behave alike at the same conditions of reduced pressure and temperature.”
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears (this needs update)
Problem Set
-
Consider Methane (Pc = 666 psia, Tc = – 117 F) and Ethane (Pc = 706 psia, Tc = – 90 F) stored in two different vessels at the following conditions:
Using the Standing-Katz Z-factor plot, determine the compressibility factor of both substances. Any observation? Are those values different? Describe the situation for both gases. If their Z-factors are the same, does it mean that both gases have the same density? What does it mean?Methane and Ethane stored in two different vessels Methane Vessel P = 1332 psia T = 55 F Ethane Vessel P = 1412 psia T = 95 F
Cubic EOS and Their Behavior (I)
Module Goals
Module Goal: To demonstrate thermodynamic quantification using modern cubic EOS.
Module Objective: To introduce you to the basis premises of cubic EOS and their behavior.
Introduction
If we multiply the vdW EOS (expression 7.11a in Module 7) by and expand the factorized product by applying the distributive law, the result is the vdW EOS expressed in terms of molar volume, as follows:
(9.1)
Note that equation (9.1) is a third order polynomial in i.e., it is cubic in molar volume. Additionally, we can substitute the definition of compressibility factor Z,
(9.2)
into equation (9.1) and obtain a different cubic polynomial in Z, as shown:
(9.3)
As we see, vdW EOS is referred to as cubic because it is a polynomial of order 3 in molar volume (and hence in compressibility factor Z). In general, any equation of state that is cubic in volume (and Z) and explicit in pressure (equation 7.11b) is regarded as a cubic equation of state. vdW EOS is a cubic EOS, and all the transformations and modifications that it has undergone during the more than one hundred years since its publication are also cubic EOS; or better, they are in-the-van-der-Waals-spirit EOS or of-the-van-der-Waals-family EOS.
The Cubic Behavior
Let us see what we have accomplished thus far. First, remember that we are not satisfied with the fact that the ideal gas law is not able to predict the discontinuity of Figure 6.3, which corresponds to the condensation that an all-gas pure substance undergoes during isothermal compression.The isotherm that we get from the ideal model was shown in Figure 6.2. Condensation, as we know, is to be expected at some point when you isothermally compress any pure gas while below its critical conditions (T < Tc). This lack of conformance to actual behavior led us to realize that the ideal model is quantitatively and qualitatively wrong at high pressures. To remove the weaknesses of the ideal model, we recall that vdW, in developing his equation of state (equation 7.11), introduced the concepts of co-volume and the attraction term.
Now, we wonder, what did he really accomplish? Are we now able to predict the condensation phenomena? Are these “new” cubic-type EOS capable of showing where such a discontinuity occurs? So far, we have not seen what a cubic isotherm looks like. Let us plot the cubic isotherm for conditions below critical (T < Tc), superimpose it on Figure 6.3, and see what we get.

Figure 9.1 shows a typical cubic behavior. That is, around condensation conditions, the equation of state presents an S-shaped curve. This should not come as a surprise; because the equation is cubic in volume, it will provide three roots for volume, and hence the S-shaped cubic feature. For the sake of our discussion, we have shown the gas and liquid branches of the cubic equation lying directly on top of the experimental ones. This kind of matching is the “ultimate goal” of any cubic EOS, but in reality, the matching is not this good — especially for the case of the original vdW EOS, as we will discuss later.
The cubic behavior is bounded by the two extremes of real fluid behavior, given by the zero pressure and infinite pressure limits. On one hand, it is clear from equation (7.11b) that we have a singularity at , where “b” represents the co-volume, or physical space that molecules themselves occupy. This singularity conveniently creates an asymptotic behavior (high pressure asymptote) of the cubic equation liquid branch, by which as . Recall from our previous discussions that predictions for are meaningless. Accordingly, we need an infinite amount of pressure if we are to compress a fluid to the extent that no free space is available among molecules . On the other hand, it is clear from vdW EOS (equation 7.11a) that as , the cubic EOS collapses to the ideal EOS (equation 7.6). At this low pressure limit, vdW
corrections to the ideal model become inconsequential .
Mathematically, this is the low-pressure asymptote of the cubic-equation gas branch by which as .
Let us see how “good” the cubic behavior is for the ideal-gas model. Refer to Figure 9.2, where we have superimposed the ideal gas isotherm of Figure 6.2 on the cubic EOS behavior.

A look at Figure 9.2 helps us confirm that the cubic equation of state collapses to the prediction of the ideal gas model at reduced pressure — i.e., they share the same low-pressure asymptote. This is to be expected, since the assumptions underlying the ideal model are satisfied. As we recall, these assumptions are that the attractive forces between molecules are very weak and that the physical volume of the molecules can be disregarded when compared to the total volume of the container. It is worthy to note that the high pressure asymptote is not the same for both models; as , as for the cubic model while for the ideal model. The latter is a direct consequence of neglecting the molecular volume in the ideal model.
Implications of S-shaped curve (Sub-critical Conditions)
A major issue that has kept us banging our heads has been how to mathematically represent the discontinuity of the P-v isotherm during the vapor-liquid transition (Figure 6.3). Such a discontinuity shows up during the isothermal compression of any pure substance at sub-critical conditions (T < Tc). What we want here requires fitting a continuous mathematical function to a discontinuous, real-life event. Strictly speaking, it would be contradictory to find a single continuous mathematical function that can capture such a discontinuity in its full nature.
Can we really model the discontinuity? Not really, but we can get around it. van der Waals provided a possible solution in his dissertation on the “continuity of vapor and liquid.” Even though neither cubic equations nor any other continuous mathematical function is able to follow the discontinuity, what they can do is good enough for engineering purposes. The “cubic behavior” can reasonably match the liquid and vapor branches for the real, experimental isotherms.
Since van der Waals’ EOS, we have been able to consider the continuity between gas and liquid phases. Now, we need to learn how to deal with the S-shaped behavior, and to look at it as a minor, inconsequential price that we pay for the modeling of the vapor — liquid discontinuous transition with a continuous mathematical function. Let us zoom in on Figure 9.1, as shown in Figure 9.3.
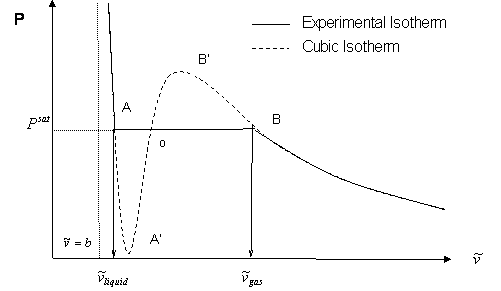
There are several features of the S-shaped behavior that should be noted.
- The S-shaped transition represents the zone where gas and liquid coexist in equilibrium for a pure substance; hence, such a behavior will show up whenever a cubic equation of state is used for predictions at temperatures below critical conditions (sub-critical conditions).
- Physically, changes in pressure and changes in volume in a fluid must have different signs in any isothermal process, such that:
This requirement is met by the liquid branch, gas branches and sections AA’ and BB’ of the cubic isotherm. Portions AA’ and BB’ have even been realized experimentally for metastable conditions, i.e., conditions of fragile or weak stability. However, changes of pressure and volume have the same sign in portion A’B’; consequently, this portion of the cubic isotherm is regarded as meaningless and unphysical. - Point A’ and B’ are the minimum and maximum values of the metastable behavior represented by the S-shaped curve. The saturation pressure (Psat) will naturally lie between these two extremes. Graphically, Psat can be attained as the pressure that make the areas AoA’ and BoB’ equal. This equal-area rule is known as the Maxwell principle. Similarly, we can also determine the saturation condition as the pressure where fugacity — a thermodynamic property we will be studying later — is equal both at the liquid and vapor branches.
- It is not impossible for section AA’ of the cubic isotherm to reach negative pressures (i.e., PA’ < 0). This should not be of any concern to us because we are seldom interested in such metastable behavior. In fact, once Psat is determined, most practical applications call for cleaning up the cubic isotherm and suppressing areas AoA’ and BoB’. In this case, we are left with liquid branch, the discontinuity AB’ at Psat, and the gas branch; just as the experimental isotherm would look.
- The most crucial implication of the S-shaped curve is that the cubic equation will certainly produce three distinct real roots for molar volume (or compressibility factor, if it is the case.) This will always be the case as long as you are making a prediction within the S-shaped curve (PA’ < P < PB’ ; T < Tc). At the vapor-liquid discontinuous transition — i.e., at the intercept of the cubic isotherm with the saturation pressure, Psat, at the given temperature — we end up with 3 mathematically possible real roots for volume. The extreme points of intersection represent liquid molar volume and gas molar volume respectively, represented as and in Fig. 9.3. The third, middle root, given by point “o”, is always regarded as unphysical and is always discarded, because it belongs to the path A’B’.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
Cubic EOS yield three roots for Z-factor for a pure substance at subcritical conditions. Does that mean that there is a “Z” factor for liquids? Isn’t the “Z” factor concept only applicable to gases? What does a “Z factor” connote for liquids?
Cubic EOS and Their Behavior (II)
Module Goals
Module Goal: To demonstrate thermodynamic quantification using modern cubic EOS.
Module Objective: To highlight the most often used cubic EOS.
Multiple Roots and Cubic Behavior
It comes as no surprise that cubic equations of state yield three different roots for volume and compressibility factor. This is simply because they are algebraic equations, and any nth order algebraic equation will always yield “n” roots. However, those “n” roots are not required to be distinct, and that is not all: they are not required be real numbers, either. A quadratic expression (n = 2) may have zero real roots (e.g., x2 + 1 = 0); this is because those roots are complex numbers. In the case of cubic expressions (n = 3), we will either have one or three real roots; this is because complex roots always show up in pairs (i.e., once you have a complex root, its conjugate must also be a solution.) In our case, and because we are dealing with physical quantities (densities, volumes, compressibility factors), only real roots are of interest. More specifically, we look for real, positive roots such that in the case of molar volume and in the case of compressibility factor.
In a cubic equation of state, the possibility of three real roots is restricted to the case of sub-critical conditions (T < Tc), because the S-shaped behavior, which represents the vapor-liquid transition, takes place only at temperatures below critical. This restriction is mathematically imposed by the criticality conditions. Anywhere else, beyond the S-shaped curve, we will only get one real root of the type . Figure 10.1 illustrates this point.
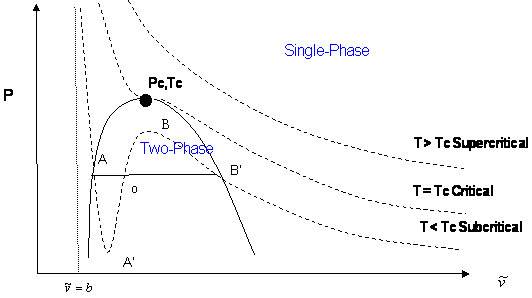
Let us examine the three cases presented in Figure 10.1:
- Supercritical isotherms (T > Tc): At temperatures beyond critical, the cubic equation will have only one real root (the other two are imaginary complex conjugates). In this case, there is no ambiguity in the assignment of the volume root since we have single-phase conditions. The occurrence of a unique real root remains valid at any pressure: any horizontal (isobaric) line cuts the supercritical isotherm just once in Figure 10.1.
- Critical isotherm (T = Tc): At the critical point (P = Pc), vapor and liquid properties are the same. Consequently, the cubic equation predicts three real and equal roots at this special and particular point. However, for any other pressure along the critical isotherm (P < Pc or P > Pc,) the cubic equation gives a unique real root with two complex conjugates.
- Subcritical isotherm (T < Tc): Predictions for pressures within the pressure range for metastability (PA’ < P < PB’) or for the saturation condition (P = Psat) will always yield three real, different roots. In fact, this is the only region in Figure 10.1 where an isobar cuts the same isotherm more than once. The smallest root is taken as the specific volume of the liquid phase; the largest is the specific volume of the vapor phase; the intermediate root is not computed as it is physically meaningless. However, do not get carried away. Subcritical conditions will not always yield three real roots of the type . If the pressure is higher than the maximum of the S-shaped curve, PB, we will only have one (liquid) real root that satisfies . By the same token, pressures between 0 < P < PA’ yield only one (vapor) root. In the case of PA’ being a negative number, three real roots are to be found even for very low pressures when the ideal gas law applies. This can be seen in Figure 10.1 as well. The largest root is always the correct choice for the gas phase molar volume of pure components.
Most of these considerations apply to the cubic equation of state in Z (compressibility factor). The most common graphical representation of compressibility factor is the well-known chart of Standing and Katz, where Z is plotted against pressure. Standing and Katz presented their chart for the compressibility factor (Z) of sweet natural gases in 1942. This chart was based on experimental data. Graphical determination of properties was widespread until the advent of computers, and thus the Standing and Katz Z-chart became very popular in the natural gas industry. Typical Standing and Katz charts are given for high temperature conditions (T > Tc or Tr > 1). Figure 10.2, using a cubic equation of state for a pure gas, presents the qualitative behavior of the solution of Z versus pressure. Isotherms (T > Tc) show the typical qualitative behavior we are accustomed to seeing in the Standing and Katz chart. Cases T < Tc (Tr < 1) are not as familiar to us, as they were not considered by Standing and Katz. For such isotherms, it is clear that you come up with two values of Z (liquid, gas) at saturation conditions.
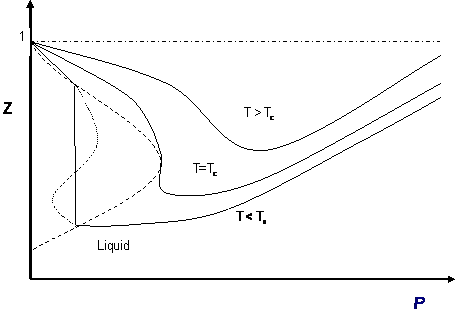
Modern Cubic EOS
At this point, we have a couple of comments on the cubic behavior that the pioneer work of vdW introduced to the field of equations of state. First, we can say that the vdW cubic behavior is qualitatively reasonable; and second, we can say that it is capable of describing the continuity between liquid and vapor. Nevertheless, vdW cubic EOS has been proven not to be quantitatively suitable for most engineering purposes. Certainly, it yields unacceptable errors for the quantitative prediction of densities and any other related thermodynamic property. However, all of the development in the field of phase behavior that has been achieved today is due to the work of van der Waals. Although his own equation is seldom used because of its lack of accuracy, his principles are still the foundations of the current developments. vdW concepts were so far reaching that he won the Nobel Prize for his equation.
The truth is that van der Waals’ accomplishment in 1873 triggered a tremendous effort among scientists to make modifications to his EOS which would remove from it large disagreements with experimental data. This effort has not yet ceased today and is not likely to stop in the near future. Much of this endeavor has focused on how to better model the attractive parameter “a” and the repulsive term “b”, with the hope that we can get better quantitative predictions. Naturally, the qualitative cubic-nature of vdW’s original EOS is always preserved, and hence all subsequent refinements belong to the same family of modified-van-der-Waals equations of state. We refer to vdW EOS and all its descendents as cubic equations of state, because, as we have said, they take a cubic form when expressed in terms of volume or compressibility factor and are explicit in pressure.
It is fair to claim that modern cubic EOS started to make a difference when a temperature dependency was introduced to the attractive parameter “a”. Interestingly enough, van der Waals was convinced that the parameters “a” (and even “b”) of his equation of state were not necessarily constants and suggested that, indeed, some dependency on temperature could be found. A very interesting discussion on this, from van der Waals himself, is found in the lecture speech that he offered during his acceptance of the Nobel Prize in Physics, in 1910, for his work on the continuity of vapor and liquid. This speech and the biography of this great physicist, Johannes Diderik van der Waals (1837-1923), can be found in the web resources of the Nobel Prize organization.
The most popular cubic EOS, which time has proven to be most reliable, are:
- Redlich-Kwong EOS,
- Soave-Redlich-Kwong EOS (very popular among chemical engineers),
- Peng-Robinson EOS (very popular among petroleum and natural gas engineers).
Keep in mind that, once you have an EOS, you can derive virtually any property of the fluid.
Redlich-Kwong EOS (1949)
vdW cubic equation of state had to wait almost 100 years before a real, successful improvement was introduced to it. As we stated before, this progress occurred once researchers committed themselves to finding the empirical temperature dependency of the attraction parameter “a” proposed by van der Waals. In contrast, very little attention has been paid to modifying the parameter “b” for co-volume. It makes a lot of sense that “b” would not be modified by temperature, because it represents the volume of the molecules, which should not be affected by their kinetic energy (measured in terms of temperature).
The very first noteworthy successful modification to the attraction parameter came with the publication of the equation of state of Redlich-Kwong in 1949. Redlich and Kwong revised van der Waals EOS and proposed the following expression:
(10.1)
Notice that the fundamental change they introduced was to the functional form of (equation 7.8, Module 7). Additionally, they introduced the co-volume “b” into the denominator of this functional form.
The important concept here is that the attraction parameter “a” of van der Waals needed to be made a function of temperature before any cubic EOS was able to do a better job of quantitatively matching experimental data. This was a realization that vdW himself had suggested, but no actual functional dependency had been introduced until the Redlich-Kwong EOS.
We know what follows at this point. To come up with an expression for “a” and “b” of equation (10.1), we apply the criticality conditions to this EOS. As we recall, imposing the criticality conditions allows us to relate the coefficients “a” and “b” to the critical properties (Pc, Tc) of the substance. Once we have done that, we obtain the definition of “a” and “b” for the Redlich-Kwong EOS,
(10.2a)
(10.2b)
This EOS radically improved, in a quantitative sense, the predictions of vdW EOS. We now recall that vdW-type equations are cubic because they are cubic polynomials in molar volume and compressibility factor. It comes as no surprise then, that we can transform equation (10.1) into:
(10.3)
and, by defining the following parameters,
(10.3a)
(10.3b)
and introducing the compressibility factor definition , we get:
(10.4)
We may also verify the two-parameter corresponding state theory by introducing equations (10.3) and (10.2) into (10.4),
(10.5)
In equation (10.5) we can observe the same thing that we saw with vdW EOS: gases at corresponding states have the same properties. Equation (10.5) is particularly clear about it: any two different gases at the same Pr, Tr condition have the same compressibility factor.
Just as any other cubic equation of state, equations (10.1) through (10.5), as they stand, are to be applied to pure substances. For mixtures, however, we apply the same equation, but we impose certain mixing rules to obtain “a” and “b”, which are functions of the properties of the pure components. Strictly speaking, we create a new “pseudo” pure substance that has the average properties of the mixture. Redlich-Kwong preserved the same mixing rules that vdW proposed for his EOS:
(10.6a)
(10.6b)
Naturally, Redlich and Kwong did not have the last word on possible improvements to the vdW EOS. The Redlich-Kwong EOS, as shown here, is no longer used in practical applications. Research continued and brought with it new attempts to improve the RK EOS. After more than two decades, a modified RK EOS with very good potential was developed. The Soave-RK EOS was born.
Soave-Redlich-Kwong EOS (1972)
In 1972, Soave proposed an important modification to the RK EOS — or shall we say, a modification to vdW EOS. Between the time of vdW EOS and Redlich-Kwong’s, a new concept for fluid characterization was being discussed. Pitzer had introduced the concept of acentric factor in 1955.
All modifications to the vdW EOS had focused on the temperature dependency of the attractive parameter. Soave expanded this by proposing a two-variable dependency for “a”:
(10.7)
It was the first time that “a” was expressed not only as a function of temperature, but also as a function of the shape (sphericity) of the molecules (through w, Pitzer’s acentric factor). As we recall, Pitzer’s acentric factor is a measure of the configuration and sphericity of the molecule. It can also be seen as a measure of the deformity of the molecule.
The Soave-Redlich-Kwong EOS is given by the expression:
(10.8a)
Like all cubic equations of state, the SRK EOS is also explicit in pressure. Notice, for example, how the SRK EOS readily becomes:
(10.8b)
where,
(10.8c)
The influence of acentric factor and temperature on the attractive term is introduced now through “a”. What do we do next? We apply the criticality conditions to equation (10.8b). Notice that expression (10.8c) becomes unity at Tr=1, throughout the critical isotherm. We obtain:
(10.9a)
(10.9b)
Now we show the cubic form (in compressibility factor) of Soave-Redlich-Kwong EOS. Defining,
(10.10a)
(10.10b)
we are able to obtain:
(10.11)
For mixtures, Soave proposed a “little” modification to the mixing rules with which we have dealt with so far by introducing the use of “binary interaction parameters” (kij):
(10.12a)
(10.12b)
The use of binary interaction parameters (kij) generated a lot of resistance upon their first introduction. This is because there is no analytical, science-based derivation that justifies their existence. Nowadays, they are regarded just as they are, empirical factors used to tune equations of state and make them match experimental data for mixtures. This has become the heuristic justification for their existence: with them, EOS can do a better job of matching experimental data. Heuristically speaking, they are a measure of interaction between a pair of dislike molecules. Based on this “definition,” their value is zero for pairs of molecules that are alike. Actually, this is no more than a mathematical requirement in order for equation (10.12a) to give when j=i. The determination of kij is based on experimental data from binary systems; “kij” results from the value that allows the given equation of state (through the expression in 10.12a) to yield the closest match. These values are assumed to be constant (and so are used) when the same two components are part of a more complex multi-component mixture.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
An engineer is seeking your advice on which EOS he should use to model various hydrocarbon mixtures he is dealing with. He has access to a program that provides him with several options for different cubic EOS. He presents you with the following list:
-
A sweet natural gas from Nigeria
- A sour natural gas (high CO2, H2S contents)
- Flue gas
-
Cubic EOS and Their Behavior (III)
Module Goals
Module Goal: To demonstrate thermodynamic quantification using modern cubic EOS.
Module Objective: To assess the relative merit of applying the most common EOS.
Peng-Robinson EOS (1976)
The Peng-Robinson EOS has become the most popular equation of state for natural gas systems in the petroleum industry. During the decade of the 1970’s, D. Peng was a PhD student of Prof. D.B. Robinson at the University of University of Alberta (Edmonton, Canada). The Canadian Energy Board sponsored them to develop an EOS specifically focused on natural gas systems. When you compare the performance of the PR EOS and the SRK EOS, they are pretty close to a tie; they are “neck to neck,” except for a slightly better behavior by the PR EOS at the critical point. A slightly better performance around critical conditions makes the PR EOS somewhat better suited to gas/condensate systems.
Peng and Robinson introduced the following modified vdW EOS:
or, explicitly in pressure,
where:
Peng and Robinson conserved the temperature dependency of the attractive term and the acentric factor introduced by Soave. However, they presented different fitting parameters to describe this dependency (equation 4.11c), and further manipulated the denominator of the pressure correction (attractive) term. As we have seen before, coefficients “a” and “b” are made functions of the critical properties by imposing the criticality conditions. This yields:
The PR cubic expression in Z becomes:
where:
Similar to SRK, the PR mixing rules are:
where binary interaction parameters (kij) again play the important empirical role of helping to better fit experimental data. Due to the empirical character of these interaction parameters, kij’s calculated for PR EOS are unlikely to be the same as the kij’s calculated for SRK EOS for the same pair of molecules.
Comparative Assessment of RK, SRK, and PR EOS
Over the years, these EOS have been tested, and some comparisons can be made. As an engineer, you have to be able to decide which EOS best fits your purposes.
Redlich Kwong EOS:
- Generally good for gas phase properties.
- Poor for liquid phase properties.
- Better when used in conjunction with a correlation for liquid phase behavior.
- Satisfactory for gas phase fugacity calculation @ Pr < Tr/3.
- Satisfactory for enthalpy departure and entropy departure calculations.
Soave Redlich Kwong & Peng Robinson EOS
- Serve similar functions as the Redlich Kwong EOS but require more parameters.
- PR obtains better liquid densities than SRK.
- Overall, PR does a better job (slightly) for gas and condensate systems than SRK. However, for polar systems, SRK always makes a better prediction, but in the petroleum engineering business we do not usually deal with those.
Zc as a Measure of Goodness of an EOS
Some values for critical compressibility factors are shown below:
Experimental Zc for Various Substances
CO2 = 0.2744
CH4 = 0.2862
C2H6 = 0.2793
nC5 = 0.2693
nC6 = 0.2659
The values of critical compressibility factors shown here are relatively close to each other, but, in actuality, they are different. They are, in fact, substance-dependent. This is a striking finding if we recall our highly-praised Principle of Corresponding States. Didn’t we say that at the same reduced conditions, all substances “must” have, at the very least, the same compressibility factor, Z? Here is a case where we have different substances at the same corresponding states (Pr = Tr = 1, right at the critical point) but different “Z” values. After all the Corresponding States Principle is not infallible (as was stated by Pitzer). As we recall, he proposed the introduction of a third parameter (acentric factor) into the corresponding state definition to alleviate these kinds of “problems.”
At the very least, we may say that the values of Zc (compressibility factor at the critical point) of different substances are “close enough” among themselves. That is, they are not “grossly different,” so as to say that the application of the two-parameter corresponding states principle would be outrageous at the critical point. The fact of the matter is, as a consequence of the Corresponding States Principle, all cubic EOS predict a “unique” and “universal” value of Z at the critical point, regardless of the substance. The list below tells us how they perform.
“Universal” Zc predicted by different EOS
Ideal EOS = 1.000
vdW EOS = 0.375
RK EOS = 0.333
SRK EOS = 0.333
PR EOS = 0.301
From the list above, we would have been expecting some kind of “average” Zc of 0.27 or so. But none of the equations of state we have studied is capable of predicting a value that low. The “best” job is done by PR EOS, which provides the “closest” match to the real values observed for most substances. This illustrates why the PR EOS performs somewhat better near critical conditions.
Advantages of Using Cubic Equations of State
All cubic equations of state have their foundation in vdW EOS. The use of cubic equations of state has become widespread because of their advantages:
- Simplicity of application
- Only a few parameters need to be determined
- Low computational overhead is required to implement them. This was a critical issue, particularly in the early stages of computers; it is not really anymore. Nevertheless, this feature is still a “plus.”
The engineer using cubic equations of state must also be aware of the disadvantages that they all share. The most important ones are the limited accuracy that they can provide, particularly for complex systems. In these cases, the procurement of empirical adjustments through the use of the binary interaction parameters (kij) is essential.
Solution Techniques for Cubic Expressions and Root Finding
Hopefully, we have convinced you that the use of cubic equations of state can represent a very meaningful and advantageous way of modeling the PVT behavior of petroleum fluids. What we need now are the tools that will allow us to get the information that we want out of them. Even though cubic equations of state are explicit in pressure, pressure is not the common unknown to be calculated in the typical problem. In the most common problem, pressure and temperature are known and we want either molar volume (or its reciprocal, molar density) or compressibility factor (the most likely case). Therefore, we are faced very often with the need to solve for the roots of a cubic expression. Here we present a number of approaches that may be followed.
Analytical scheme
Given the cubic polynomial with real coefficients: x3 + ax2 + bx + c = 0, the first step is to calculate the parameters:
(11.5)
Now let M = R2 – Q3 be the discriminant. We then consider the following cases:
-
If M < 0 (R2 < Q3), the polynomial has three real roots. For this case, compute and calculate the three distinct real roots as:
(11.6a)
(11.6b)
(11.6c)
Note that x1, x2, x3 are not given in any special order, and that has to be calculated in radians.
-
If M > 0 (R2 > Q3), the polynomial has only one real root. Compute:
(11.7a)
(11.7b)
and calculate the real root as follows:(11.7c)
Two complex roots (complex conjugates) may be found as well. However, they are of no interest for our purposes, and thus no formulas are provided. Such formulas can be found in the following suggested readings:
- W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery, Numerical Recipes in Fortran, 2nd Edition, Cambridge Univ. Press, (1992), p. 179.
- Spiegel, M., Liu, J., Mathematical handbook of formulas and tables, 2nd Edition, Schaum’s Outline Series, McGraw Hill, p.10.
Sometimes, the equations for S and T listed above cause problems while programming. This usually happens whenever the computer/calculator performs the cubic root of a negative quantity. If you want to avoid such a situation, you may compute S’ and T’ instead:
(making T’=0 when S’=0)
where:
abs(R) = Absolute value of R
and
sign(R) = (+1) or (– 1) if R is positive or negative respectively.
It may be defined as:
sign(R) = R/Abs(R)
and then the real root is:
Keep in mind the following useful relationships among the roots of any cubic expression:
(11.8a)
(11.8b)
(11.8c)
Self-Check
Test your understanding of cubic root calculations by analytical means by solving the following examples.
With general cubic expressions,
with EOS in terms of volume (v), for a pure component,
=> One real root (one phase),
Another example,
=> Two possible phases (three real roots),
with EOS in terms of the compressibility factor (z), for a pure component,
=> One phase,
Another example,
=> Two possible phases,
Numerical Scheme
The Newton-Raphson method provides a useful scheme for solving for a non-explicit variable from any form of equation (not only cubic ones). Newton-Raphson is an iterative procedure with a fast convergence, although it is not always capable of providing an answer — because a first guess close enough to the actual answer must be provided.
In solving for “x” in any equation of the type f(x)=0, the method provides a new estimate (new guess) closer to the actual answer, based on the previous estimate (old guess). This is written as follows:
(11.9)
Considering a cubic equation , the previous equation takes the form:
(11.10)
The iterations continue until no significant improvement for “xnew” is achieved, i.e., | xnew – xold | < tolerance. An educated guess must be provided as the starting value for the iterations. If you are solving a cubic equation in Z (compressibility factor), it is usually recommend to take Z = bP/RT as the starting guess for the compressibility of the liquid phase and Z = 1 for the vapor root.
Semi-analytical Scheme
If you used the previous numerical approach to calculate one of the roots of the cubic expression, the semi-analytical scheme can give you the other two real roots (when they exist). By using the relationships given before, with the value ‘x1’ as the root already known, the other two roots are calculated by solving the system of equations:
(11.11a)
(11.11b)
which leads to a quadratic expression.This procedure can be reduced to the following steps:
-
Let be the original cubic polynomial and “E” the root which is already known (x1 = E). Then, we may factorize such a cubic expression as:
(11.12a)
where:
(11.12b)
(11.12c)
-
Solve for x2, x3 by using the quadratic expression formulae,
(11.13a)
(11.13b)
(11.13c)
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
What is the meaning of Zc? (critical compressibility factor). Why do you think it is used as a measure of the performance of an EOS?
-
What do you think should be the value of “Z” at the critical point? Is it “one” (1)? Why? Is this to be expected?
Elementary Vapor-Liquid Equilibrium (I)
Module Goals
Module Goal: To establish the basic framework for vapor-liquid equilibrium calculations.
Module Objective: To establish the connection between real production processes and vapor liquid equilibrium calculation.
Introduction
In the next series of modules, we are going to look at how we can apply what we have learned so far to perform vapor/liquid equilibria calculations.
- First of all, we are going to review engineering systems and how the phenomenon of VLE is related to them,
- Then we will proceed by looking at how to describe the problem itself,
- We then will discuss the formulation the problem,
- And finally, we will discuss solution strategies.
These are the four main topics that we will look at in this module. As far as VLE is concerned, we can list a number of systems that are at the heart of petroleum fluid production that involve this phenomenon:
- Separators
- Reservoir
- Pipelines
- Wellbore
- LNG Processing
- NGL Processing
- Storage
- Oil and LNG Tankers.
Vapor/liquid equilibrium pertains to all aspects of petroleum production with which we are concerned. It is no wonder, then, that we devote a new module to the subject itself.
Consider the case of a typical transmission pipeline. As gas is injected at the inlet, the pressure will drop continuously along the length of the pipeline, due to friction. Even though we usually think of liquid as forming with increasing pressure — i.e., upon compression — we have to recall that the phenomena of retrograde condensation (discussed in Module 4) takes place in hydrocarbon mixtures. Therefore, contrary to expectations, most single-phase natural gasses yield liquid upon expansion. Therefore, as pressure drops in the pipeline, liquid may drop out as the thermodynamic path crosses the dew point line and enters the phase envelope. In this case, what started as a single phase flow became two-phase flow within the system.
We also encounter this phenomenon in gas condensate reservoirs. Your initial reservoir conditions may be outside the phase envelope, but as you deplete the reservoir, your production path may take the system inside the two-phase region. In these previous two examples, the single-most important property with which you are concerned is the dew point. You want to know dew point, since you would like to know at which point of the pipeline or at which stage of production liquid may start to form.
We also may have an oil reservoir, where the initial pressure and temperature conditions place us in the single-phase liquid region. As you produce, you deplete the reservoir and enter the two-phase region by crossing the bubble point curve. At this point, we would like to know the bubble point of the system so that we may anticipate the appearance of a gas phase within an originally-all-liquid reservoir.
In all these cases, by taking a sample of the fluid to the lab, we may be able to find the composition of the fluid. Hence, in these kinds of problems, composition is usually known, and so are temperature and pressure. Your unknowns are the dew point or bubble point condition.
Suppose we are not interested in what is happening in the reservoir, but rather in what is happening at the surface. You would then like to know how much liquid or gas you will have in your separators. In this case, you are no longer interested in bubble points or dew points, but rather the extent of the phases: how much liquid and how much gas the reservoir will be able to deliver at the surface. In this case, the composition of what is coming to your separator may be known, and the pressure and temperature of operation of each separation stage may be specified. We would want to know the quality and the quantity of what is coming out; that is, we need the compositions of the gas and oil that leave the separators and the flow rates of gas (MSCF/D) and oil (STB/D).
Types of VLE Problems
In a typical problem of liquid and vapor coexistence, we are usually required to know one or more of the following:
- The phase boundaries,
- The extent of each phase,
- The quality of each phase.
The main emphasis is on the quantitative prediction of the above. These three represent the three basic types of VLE problems. A more detailed description of each of them is given below.
- Phase Boundary Determination Problem
These types of problems are either a bubble-point or a dew-point calculation. They are mathematically stated as follows:
- Bubble-point T calculation: Given liquid composition (xi) and pressure (P), determine the equilibrium temperature (T),
- Bubble-point P calculation: Given liquid composition (xi) and temperature (T), determine the equilibrium pressure (P),
- Dew-point T calculation: Given vapor composition (yi) and pressure (P), determine the equilibrium temperature (T),
- Dew-point P calculation: Given vapor composition (yi) and temperature (T), determine the equilibrium pressure (P).
- Relative Phase Quantity Determination
In this type of problem, overall composition (zi), pressure (P), and temperature (T) are given, and the extent of the phases (molar fractions of gas and liquid) are required.
- Phase Quality Determination
In this type of problem, overall composition (zi), pressure (P), and temperature (T) are given, and the composition of the liquid and vapor phases is required.
Problems of types 2 and 3 are collectively referred to as flash calculation problems. All three are problems that we encounter in production operations as petroleum engineers. Our focus now is on solving these sorts of problems. We want to use a predictive approach to do so. This is, we want to use mathematical models — the most economical and convenient approach — to accomplish the task.
One of the assumptions that we are making here is that of equilibrium. We assume that at all times, vapor and liquid that are coexisting together are in equilibrium. Are they really in equilibrium? No! Nevertheless, the state of current knolwedge requires us to assume equilibrium so as to be able to proceed.
Formulation of the VLE Problem
We assume that the system is at steady state and at a state of equilibrium. Adopting these two assumptions is essential to the developing of the equations that we use to solve these problems. These assumptions are convenient for modeling and have proven useful in representing the real phenomena. In conclusion, we claim that the systems maintain a state that resembles equilibrium and does not depart from it greatly. And what does steady state means? Simply stated, we say that a system is at steady state when whatever comes into the system goes out. This is, no accumulation takes place within the system.
Let us consider the equilibrium cell shown in Figure 12.1. “F” moles of a feed enter our equilibrium cell with a composition “zi” and “nc” is the number of components that we have in the mixture. A flash vaporization takes place at a given pressure and temperature, and two streams come out: “V” moles of a vapor of composition “yi” and “L” moles of a liquid of composition “xi”. In steady state, a simple overall balance yields:
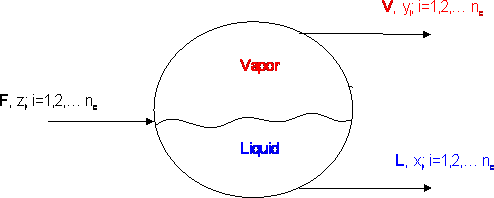
(12.1a)
Now we define the fractions of gas and liquid to be, respectively:
(12.1b)
(12.1c)
Therefore, if we divide equation (12.1a) by “F”, we get:
(12.2)
The same steady state assumption applies for the mass of each component separately. Here we revisit a concept we used in Module 5, when we studied the lever rule. At that point, we said that the number of moles of a component “i” per mole of mixture in the liquid phase is given by the product “xiaL”, while the number of moles of “i” per mole of mixture in the gas is given by “yiaG”. Since there are “zi” moles of component “i” per mole of mixture coming into the system, the conservation of each component in the system imposes:
(12.3)
Equation (12.3) is true for each of the components in the system. Equation (12.2) can be introduced into equation (12.3) to yield:
(12.4)
One of the concepts that we normally use in vapor-liquid equilibria is that of the equilibrium ratio, Ki. In fact, most of the computations of phase behavior of natural gas mixtures are carried out through the concept of the equilibrium ratio. By definition, the equilibrium ratio of a component “i” in a vapor-liquid mixture is defined as the ratio of the molar composition of that component in the vapor phase to that in the liquid phase,
(12.5)
In earlier literature, this concept was referred to as the equilibrium constant. In actuality, Ki is not constant but a function of the pressure, temperature, and composition of the system. However, equilibrium ratios can be fairly independent of composition when the pressure and temperature conditions are far from critical.
Therefore, today we refer to it as the vapor-liquid equilibrium ratio, Ki. We can introduce this concept into the balance in (12.4), as shown:
(12.6)
Now, solving for yi,
(12.7)
A constraint that mole fractions must satisfy is that they must add up to unity. Since we solved for yi, we can impose that the summation of all molar vapor fractions must be equal to one, i.e.,
(12.8)
If we now substitute (12.7) into (12.8), we get:
(12.9)
This equation is important for us; we call it an objective function because we can use it as the starting point for solving the vapor-liquid equilibrium problems we have posed.
However, as you may be thinking right now, this is not the only choice that we have for an objective function. In fact, we may obtain another objective function if we repeat the previous steps, while solving instead for xi. In this case, we may introduce the concept of equilibrium ratio in (12.5) into (12.6) as follows:
(12.10)
We now solve for xi,
(12.11)
If we apply the constraint that all mole fractions must add up to one,
(12.12)
Both (12.9) and (12.12) are plausible objective functions. Either of them allows us to solve the flash problem that we are dealing with. The variables that make up both equations are:
nc = Number of components,
zi = Overall composition, or composition of the feed,
Ki = Equilibrium ratios of each of the components of the mixture,
ag = Vapor fraction in the system.
What is it that we are looking for? Go back and look at the types of VLE problems that we would like to solve, as we presented them in the previous section. If we are interested in solving the flash problem, we want to know how much liquid and gas we will have inside the flash equilibrium cell. This is, given a liquid-vapor mixture of composition zi, and nc number of components, what percent of the total number of moles is liquid, and what percent is vapor? How do we split it? In this case, we would like to come up with a value for αl and αg respectively.
Equations (12.9) and (12.12) tell us that if we are able to come up with the proper values for the equilibrium ratios, Ki, which are functions of the pressure, temperature, and composition of the system, the only unknown left to solve for would be αg — exactly what we want!
Well, do not rush. We would have to come up with a way of calculating Ki’s first, and this may not be a trivial task. For the time being, let us say we “know” Ki’s. Two questions remain unanswered:
- First, is it “better” to solve the problem using equation (12.9) or (12.12)? (Recall, either of them would lead us to the answer!).
- Second, how do we solve for αg? For a complex mixture of many components, “αg” cannot be calculated explicitly.
We will address both of these questions in the next module. As for now, let us give you a hint: we will not use either equation (12.9) or (12.12) to solve the flash problem!
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
You are given two different phase envelopes (VLE region) that represent two different gas reservoir fluids. The first of them has a larger PT envelope covering larger P,T ranges. The other covers a fairly narrow P,T range. What do you conclude? Speculate on the type of gas reservoir for each case. Justify your answer.
-
In order to design the appropriate production scheme for a gas reservoir recently discovered, what type of VLE calculation do you think is more valuable? Explain in detail.
Elementary Vapor-Liquid Equilibrium (II)
Module Goals
Module Goal: To establish the basic framework for vapor-liquid equilibrium calculations.
Module Objective: To formulate the basic governing equations for performing flash calculations.
Analysis of Objective Functions
In a previous module we derived two different objective functions for the purpose of solving the flash equilibrium problem. Let us take a closer look at these equations:
(13.1a)
(13.1b)
These equations arise from simple mole balances and the concept of equilibrium ratios. As we discussed before, if we are given {zi; i = 1,2,…,n} and, if for some reason, let us say, we are able to obtain all the equilibrium ratios {Ki; i = 1,2,…,n}; the only unknown in these objective functions would be the vapor fraction ‘’.
Once we are able to solve for this , we will have no problem applying any combination of equations (12.5), (12.7), and (12.11) to solve for all the vapor and liquid compositions at equilibrium {yi, xi}:
(12.5)
(12.7)
(12.11)
With all this information, the VLE problem would be completely solved. With the compositional information and the use of suitable equations of state and correlations, we can then find all other related properties, such as densities, viscosities, molecular weights, etc. This is why we call these the objective functions once we have solved them, we have achieved the objective of the VLE calculation.
Of course one question remains unanswered — how do you solve for that ‘ g’, which is buried inside those expressions? And secondly, which of the two objective functions that are available to us shall we use? It turns out that the answers to these questions are tied to one another. In fact, the proper objective function that we shall use to solve for ‘g’ is the same equation that simplifies the process of solving for that unknown.
To come up with these answers, the first thing that we have to notice is that both expressions are non-linear in g. This means that we cannot express ‘g’ explicitly as a function of the other variables. What do we use to solve equations that are non-linear in one variable? Doesn’t this ring a bell? We apply iterative techniques. And the classical iterative technique is the Newton-Raphson procedure. Now we can provide an answer to both of the questions that we just asked.
A distinctive characteristic of any Newton-Raphson procedure is that the success of the procedure depends greatly upon the choice of the initial guess for the variable considered. In fact, it is very commonly said that for Newton-Raphson to succeed, the initial guess must be as close as possible to the real solution. This ‘illness’ becomes worse when dealing with non-monotonic functions. In a monotonic function, derivatives at every point are always of the same sign — the function either increases or decreases monotonically. For Newton-Raphson, this means that there are neither valleys nor peaks that could lead the procedure to false solutions. If you apply Newton-Raphson to a monotonic and everywhere-continuous function, the success of the procedure is not dependent on the initial guess. In fact, if you apply Newton-Raphson to a monotonic function that is continuous at every single point of the domain as well, it does not matter at all where you start: you will always find the solution. It might take time, but you will be able to converge to a unique solution.
Why does this matter when dealing with equations (13.1)? The fact of the matter is that equations (13.1) are not monotonic, and this does not make things easier. If, as an exercise, you plot them as a function of g or take the derivative, you will realize that both functions may change the sign of their first derivatives for different values of g.
This poses a problem, obviously. You will not get a unique solution by applying Newton-Raphson, and you might end up with the wrong solution. Rachford and Rice (1952) recognized this problem and came up with a suggestion. They proposed a new objective function, based on equations (13.1), which simplifies the application of the Newton-Raphson procedure.
They combined equations (13.1) by subtraction to yield:
(13.2)
Hence, the new objective function becomes:
(13.3)
Equation (13.3) is known in the literature as the Rachford-Rice Objective Function. Rachford and Rice combined two very well known objective functions into a single objective function. Are there advantages to this “new” approach?
The wonderful news is that equation (13.3) is monotonic. The implication of this is that equation (13.3) is better suited for Newton-Raphson application than equations (13.1). How do you demonstrate the monotonic character of the Rachford and Rice objective function? To do this, we take the first derivative of the function:
(13.4)
Every item within the summation sign is positive — this is guaranteed by the squares in the numerator and the denominator and the fact that all compositions are positive. Hence, the derivative expression in (13.4) has no choice but to be negative, and the Rachford-Rice Objective function has been proven to be a monotonically decreasing function. With this approach, Rachford-Rice removed a major headache from the Vapor-Liquid Equilibria problem.
A remaining weakness of the Rachford-Rice objective function is that, although monotonic, it is not continuous at all points of the domain. By inspection, you can see that the function has ‘n’ singularities (as many singularities as components in the mixture), because it becomes singular at values of ‘ ’ equal to:
(13.5)
Hence, you may still face convergence problems if the procedure crosses any of the singularities. If, by any means, one is able to keep the Newton-Raphson procedure within values of where a physically meaningful solution is possible (within the two asymptotes where the values 0 < < 1 are found), the monotonically decreasing feature of the Rachford-Rice equation would guarantee convergence.
Objective Function and Newton-Raphson Procedure
We have seen that from a molar material balance applied to a two-phase system in equilibrium, and the definition of Ki, we can derive the Rachford and Rice Objective Function:
(13.3)
Equation (13.3) is a non-linear equation in one variable, and the Newton Raphson procedure is usually implemented to solve it. In general, Newton Raphson is an iterative procedure with a fast rate of convergence. The method calculates a new estimate, , which is closer to the real answer than the previous guess, , as follows:
(13.6)
Substituting (13.3) and (13.4) into (13.6),
(13.7)
In this iterative scheme, convergence is achieved when
(13.8)
where is a small number ( is usually adequate). After solving for , the liquid molar fraction and composition of each of the phases can be calculated as follows:
(13.9a)
(13.9b)
(13.9c)
(12.7)
(12.11)
Do We Really Know Ki?
The Need For More Advanced Tools
In the previous development, we made one crucial assumption. We assumed that, somehow, we knew all the equilibrium ratios. The fact is, however, that we usually don’t. If we do not know all equilibrium ratios, then all of the previous discussion is meaningless. So far, the only conclusion we can draw is that if we happen to know Ki’s, the VLE problem is solvable.
The Ki value of each component in a real hydrocarbon mixture is a function of the pressure, temperature, and also of the composition of each of the phases. Since the compositions of the phases are not known beforehand, equilibrium constants are not known, either. If they were known, the VLE calculation would be performed in a straightforward manner. This is because once the equilibrium constants of each component of the mixture are known for the given pressure and temperature of the system, both gas and liquid molar fractions, and al can be calculated by solving the Rachford-Rice Objective Function.
Nevertheless, the good news is that sometimes Ki’s are fairly independent of the phase’s composition. This is true at pressure and temperature conditions away from the critical point of the mixture. Therefore, numerous correlations have been developed throughout the years to estimate the values of Ki for each hydrocarbon component as a function of the pressure and temperature of the system.
To illustrate how Ki may be calculated as a function of pressure and temperature, let us take the case of an ideal mixture. For a mixture to behave ideally, it must be far removed from critical conditions. The fact of the matter is, in an ideal mixture, the partial pressure of a component in the vapor phase (pi) is proportional to the vapor pressure (Psat) of that component when in its pure form, at the given temperature. The constant of proportionality is the molar fraction of that component in the liquid (xi). Then, we have:
(13.10)
Equation (13.10) is known as Raoult’s law. Additionally, if the vapor phase behaves ideally, Dalton’s law of partial pressures applies. Dalton’s law of partial pressures says that the total pressure in a vapor mixture is equal to the sum of the individual contributions (partial pressures) of each component. The partial pressure of each component is a function of the composition of that component in the vapor phase:
(13.11)
Equalizing equation (13.10) and (13.11),
(13.12)
We rearrange equation (13.12) to show:
(13.13)
If we recall the definition of equilibrium ratios, , we readily see:
(13.14)
Since the vapor pressure of a pure substance (Psat) is a function of temperature, we have just shown with equation (13.14) that the equilibrium ratios Ki are functions of pressure and temperature — and not of composition — when we are dealing with ideal substances. Vapor pressure can be calculated by a correlation, such as that of Lee and Kesler.
The estimation of equilibrium ratios (Ki) has been a very intensely researched subject in vapor-liquid equilibria. A number of methods have been proposed in the literature. In the early years, the most common way of estimating equilibrium ratios was with the aid of charts and graphs that provided Ki values as a function of pressure and temperature for various components. Charts provided better estimations of Ki’s than what came from the direct application of Raoult-Dalton’s derivation (equation 13.14). However, the compositional dependency could not be fully captured by the use of charts. Charts remained popular until the advent of computers, when the application of more rigorous thermodynamic models became possible.
Most of the Ki-charts available have been represented by empirical mathematical correlations to make them amenable for computer calculations. You may find a large number of correlations in the literature that would allow you to estimate Ki’s for a range of conditions. A very popular empirical correlation that is very often used in the petroleum and natural gas industry is Wilson’s empirical correlation. This correlation gives the value of Ki as a function of reduced conditions (Pri, Tri: reduced pressure and temperature respectively) and Pitzer’s acentric factor and is written as:
(13.15)
Wilson’s correlation is based on Raoult-Dalton’s derivation (equation 13.14). Therefore, it does not provide any compositional dependency for Ki’s and, as such, it is only applicable at low pressures (away from the critical conditions). We have included this correlation not because of its accuracy, but because it will become the initial guess that is needed to start the Ki-prediction procedure, which we will develop later.
In the following modules, we will develop a rigorous thermodynamic model for predicting equilibrium ratios. As you may anticipate, we will be taking advantage of what we have learned about equations of state in order to build up a phase behavior predictor model. This approach is known as the equation of state approach, or the “fugacity” approach. Even though the “fugacity” approach is the one that we will be covering in detail, you may at some point encounter the fact that equilibrium ratios can also be estimated by using the solution theory or “activity” approach. We will not be discussing the latter, as the former represents the most popular Ki-prediction method in the petroleum and natural gas business.
In order to guarantee a complete understanding of the thermodynamic model which we are about to apply, we need to review the basic concepts of classical thermodynamics. This is the goal for the next couple of modules (Modules 14 through 16). After all of the thermodynamic tools have been given to the reader, we will resume our discussion of Vapor-Liquid Equilibria (Module 17), along with discussing how equations of state come into the picture. Our final goal will be to tie the equilibrium ratio, Ki, to the thermodynamic concepts of chemical potential, fugacity, and equilibrium.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
In the older literature, “Ki” were referred to as the “equilibrium constants.” Now, they are called the “equilibrium ratios.” Why should that make a difference?
-
In the analysis of the Rachford-Rice Objective Function, we assumed that there was only one unknown: the gas molar fraction (αg). It this strictly true?
- Warren and Adewumi (1992) derived the following analytical expression for flash calculations for a binary mixture:
Please demonstrate that this expression is true.
Thermodynamic Tools (I)
Module Goals
Module Goal: To establish the mathematical framework for thermodynamics of phase equilibrium.
Module Objective: To highlight the importance of thermodynamic functions as functions of state.
Introduction
Thermodynamics plays an important role in science and engineering. Most physical processes of engineering interest operate on thermodynamic principles. Thermodynamics is the science dealing exclusively with the principles of energy conversion. This message is conveyed by the word itself: “thermo” means “heat” — a manifestation of energy — and “dynamics” deals with “motion.”
Often times, we do not use thermodynamics as much as we should. This is either because we do not know how useful a tool it can be, or, simply because we do not know how to use it.
The basic ingredients for the utilization of thermodynamics are:
- The ability to identify and define the system that best characterizes a given process
- The availability of relevant information
- Sound engineering judgment
The goal of this module, combined with all the background that we already have built on fluid behavior, is to establish a foundation for us to cultivate a culture of the appropriate utilization of thermodynamics.
What kinds of problems can be solved with thermodynamics? There are three general classes of thermodynamic problems.
- System property variation determination. In this case, we are given a process that takes place under certain known constraints. We are required to determine how the system properties vary.
- Interactions that cause change. In these kinds of problems, the changes desired in the system properties are prescribed. We are required to determine the amount of external interactions that are needed to cause these changes — i.e., how to vary constraints to obtain the required final system state.
- The best-path problem. Here we are given a system with constraints and a desired variation. We are required to determine the best way to accomplish the change — i.e., the best way to reach a goal.
In science and engineering, mathematical rigor is of essence. The next sections will take us through the mathematics of thermodynamics.
Basic Definitions
In thermodynamics, a system is a spatial domain bounded for the purpose of describing a problem; while the surroundings are the entire spatial domain outside of the system. The communication between them is established through the of the system. The system and the surroundings make up the universe.
The system and the surroundings interact with each other. As we discussed above, one type of thermodynamic problem is that of predicting changes in a system due to interactions with its surroundings. A system is open if it can exchange mass with the surroundings, and closed if it does not exchange mass with the surroundings. A system is adiabatic if it does not exchange heat energy with the surroundings. We called a system isolated if there is neither heat nor mass crossing its boundaries.
Thermodynamic properties can be divided into two general classes: intensive and extensive properties. An intensive property is one whose value is independent of the size, extent, or mass of the system, and includes pressure, temperature, and density. By contrast, the value of an extensive property changes directly with the mass. Mass and volume are examples of extensive properties. Extensive properties per unit mass, such as specific volume, are intensive properties.
A system is homogeneous if it is has uniform properties throughout, i.e. a property such as density has the same value from point to point in a macroscopic sense. A phase is defined as a quantity of matter that is homogeneous throughout. Hence, a homogeneous system is, essentially, a single-phase system. A heterogeneous system is one with non-uniform properties, and hence, is made up of phases which can be distinguished from one another by the presence of interfaces.
Thestate is the thermodynamic coordinate of the system, specified by a number of intensive variables. The degree of freedom is the number of intensive variables needed to define the state of the system. State functions are those whose changes depend on their end states only and are independent of the path between them.
A process is the series of successive, intermediate states that the system goes through in order to go from an initial to a final state. A process is isothermal or isobaric if the temperatures or pressures of all successive steps are the same, respectively. A reversible process is one for which the exchange of energy between the system and its surroundings takes place under vanishing gradients or driving forces; that is, the properties of the system and surroundings are balanced. In a reversible process, each step of the process can be “reversed” and the original states of the system and surroundings can be restored. Any process that does not take place under infinitesimal gradients is irreversible. Strictly speaking, a reversible process is an idealization.
Thermodynamics of Systems of Constant Composition (Closed Systems)
Thermodynamics cannot tell about the rate (kinetics) of a process, but it can tell whether or not it is possible for a process to occur. For this, we make use of the first and second laws of thermodynamics.
From our basic courses in thermodynamics, we recall that the first law of thermodynamics for a closed system is written as follows:
(14.1)
where,
U = internal energy,
Q = heat added to or extracted from the system,
W = work done by or to the system.
If we want to improve the definition of the first law of thermodynamics stated in (14.1), we need to come up with an expression for the amount of work and heat. The amount of work need to accomplish a reversible process is given by the expression:
(14.2)
where:
P = pressure,
V = volume.
Additionally, we can compute the heat required to accomplish a reversible process by virtue of the second law of thermodynamics:
(14.3)
where:
T = temperature,
S = entropy.
We substitute (14.2) and (14.3) into (14.1) to get:
(14.4)
which is the fundamental thermodynamic relationship used to compute changes in Internal Energy (U) for a closed system. This is only a restatement of the first law of thermodynamics.
Although equations (14.2) and (14.3) are applicable strictly to reversible processes, equation (14.4) is quite general and does not have such a constraint. Equation (14.4) applies to reversible and irreversible processes. Are you surprised by this? Okay, it is about time that we start to get a feeling for the implications of the fact that most thermodynamic properties are state functions. Internal energy (U) is a state function, and as such, its changes (dU) do not depend on the path that was taken (reversible/irreversible), but on the end points of process. Hence, if taking any path to compute “dU” is okay, why not take the reversible path? We do not have nice, explicit equations to describe work and heat for irreversible processes. Why should we bother? Generally speaking, “reversibility” is a thermodynamic trick that helps us to get away with many thermodynamic manipulations by taking advantage of the properties of state functions.
The formal, fundamental thermodynamic definition of Enthalpy (H) is the following:
H = U + P (14.5)
Enthalpy is a state function as well. If we are interested in computing changes in enthalpy, we write:
(14.6)
Since we already have a way to compute dU (equation 14.4), we can now write the fundamental thermodynamic relationship used to compute changes of enthalpy in a closed system:
By the same token, the formal, fundamental definition of Gibbs Free Energy (G) is the following:
(14.8)
from which we see that changes in this property may be calculated as:
(14.9a)
We now substitute (14.7) to get the fundamental thermodynamic relationship for changes in Gibbs free energy in a closed system:
(14.9b)
We proceed with Helmholtz Free Energy (A) accordingly. Its definition:
(14.10)
The expression of change,
(14.11)
We substitute (6.4) into it and get:
(14.12)
We have just derived the following fundamental thermodynamic relationships for fluids of constant composition:
(14.4)
(14.7)
(14.9)
(14.12)
All these properties (U, H, G and A) are state functions and extensive properties of the system. Notice that the only assumption that we took throughout their development is that the system was closed (for the derivation of 14.4). Hence, these equations strictly apply to systems of constant composition.
Functions of State or State Functions
A function of state is one in which the differential change is determined only by the end states and not by intervening states. Most thermodynamic variables are state functions and hence property changes are determined by the end states and not by the process path. Notable exceptions are work and heat.
The most common thermodynamic state functions with which we shall deal include
- Internal Energy (U),
- Entropy (S),
- Enthalpy (H),
- Helmotz Energy (A), and
- Gibbs Energy (G).
Mechanics of Manipulating a Function of State
Given that f(x,y,z) is any state function that characterizes the system and (x,y,z) is a set of independent variable properties of that system, we know that any change f will be only a function of the value of “f” at the final and initial states,
(14.13)
Since f=f(x,y,z), we can mathematically relate the total differential change (df) to the partial derivatives , , and of the function, as follows:
(14.14)
where, in general:
the change of f with respect to x, while y and z are unchanged.
If we want to come up with the total change, , of a property (we want to go from 14.14. to 14.13), we integrate the expression in (14.14) to get:
(14.15)
Let us visualize this with an example. For a system of constant composition, its thermodynamic state is completely defined when two properties of the system are fixed. Let us say we have a pure component at a fixed pressure (P) and temperature (T). Hence, all other thermodynamic properties, for example, enthalpy (H), are fixed as well. Since H is only a function of P and T, we write:
(14.16)
and hence, applying 6.2, any differential change in enthalpy can be computed as:
(14.17)
The total change in enthalpy of the pure-component system becomes:
(14.18)
Now we are ready to spell out the exactness condition, which is the mathematical condition for a function to be a state function. The fact of the matter is, that for a function to be a state function — i.e., its integrated path shown in (14.15) is only a function of the end states, as shown in (14.13) — its total differential must be exact. In other words, if the total differential shown in (14.14) is exact, then f(x,y,z) is a state function. How do we know if a total differential is exact or not?
Given a function (x,y,z),
(14.19a)
where:
(14.19b)
(14.19c)
(14.19d)
we say that is an exact differential and consequently a state function if all the following conditions are satisfied:
(14.20a)
(14.20b)
(14.20c)
Equations (14.20) are called the exactness condition.
Computing Property Changes in Closed Systems
Now we recall the fundamental thermodynamic relationships for closed systems, which we derived above:
where U, H, G, and A are state functions. There is something remarkable about the above expressions: they allow for the direct calculation of the change in a state function as a function of changes in other two. An important lesson to be learned here: when dealing with thermodynamic state properties, we are most interested in changes in the value of state properties rather than their actual values.
As we have said, the above relationships allow us to visualize that the changes of each thermodynamic property are dependent on the change of two others in a closed system.
Therefore, recalling what we did in equation (14.14), we express the total differential of each of these properties as:
Comparing these equations term to term, the following realizations can be made:
Additionally, we can go one step further. U, H, G, and A are state functions, and as such, their total differentials (equations 14.4, 14.7, 14.9, and 14.12) must be exact. Recall that for a total differential df=Mdx+Ndy to be an exact differential, it must satisfy the equation:
Equation (14.24) is the exactness criteria for a function of two independent variables. It was previously stated in (14.20) for a state function of three independent variables. Its application yields:
Equations (14.25) are known as Maxwell’s relationships. Maxwell’s relationships are very useful for manipulating thermodynamic equations. For instance, it is always desirable for practical purposes to express thermodynamic properties such as enthalpy (H) and entropy (S) as functions of measurable properties such as pressure (P) and temperature (T):
Starting with the total differential of H and S as a function of P and T, we can prove that the relationships between the parameters H and S and the parameters P and T are given by the expressions:
Additionally, since these expressions for dH and dS must also be exact differentials, you could prove that the heat capacity at constant pressure (CP) for an ideal gas (PV = RT) does not depend on pressure. The thermodynamic definition of CP and Cv are:
The heat capacity at constant volume (CV) for an ideal gas does not depend on pressure, either. You could prove this by proving first that Cp=CV+R (R=universal gas constant) for ideal gases, using above tools.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
In you own words, state how you would explain the implications of the 1st law and 2nd law of thermodynamics. Assume that you need to explain this to a 5 year old child that has no idea about thermodynamic jargon.
-
Suppose that most thermodynamic properties were not state functions. What impact would that have in process design?
Thermodynamic Tools (II)
Module Goal:
To establish the mathematical framework for thermodynamics of phase equilibrium.
Module Objective:
To establish that there is an unique relationship between partial molar quantities in any mixture.
Homogeneous Functions, Euler's Theorem and Partial Molar Quantities
Any function f(x) that possesses the characteristic mapping:
is said to be homogeneous, with respect to x, to degree 1. By the same token, if f(x) obeys the mapping:
then f(x) is homogeneous to degree “k”. In general, a multivariable function f(x1,x2,x3,…) is said to be homogeneous of degree “k” in variables xi(i=1,2,3,…) if for any value of ,
For example, let us consider the function:
How do we find out if this particular function is homogeneous, and if it is, to what degree? We evaluate this function at to obtain:
hence, the function f(x,y) in (15.4) is homogeneous to degree -1.
In regard to thermodynamics, extensive variables are homogeneous with degree “1” with respect to the number of moles of each component. They are, in fact, proportional to the mass of the system to the power of one (k=1 in equation 15.2 or 15.3). This is, if we triple the amount of mass in the system, the value of any given extensive property will be tripled as well. Notice that this is not the case for intensive properties of the system (such as temperature or pressure), simply because they are independent of mass. Hence, intensive thermodynamic properties are homogeneous functions with degree “0” — in such a case, k=0 in equation (15.2) or (15.3).
From the previous section, it is clear that we are not only interested in looking at thermodynamic functions alone, but that it is also very important to compute how thermodynamic functions change and how that change is mathematically related to their partial derivatives . Hence, to complete the discussion on homogeneous functions, it is useful to study the mathematical theorem that establishes a relationship between a homogeneous function and its partial derivatives. This is Euler’s theorem.
Euler’s theorem states that if a function f(ai, i = 1,2,…) is homogeneous to degree “k”, then such a function can be written in terms of its partial derivatives, as follows:
Since (15.6a) is true for all values of , it must be true for . In this case, (15.6a) takes a special form:
So far, so good. But…what is the application of all this? Well, first of all, we have to know something more about extensive thermodynamic properties. A very neat thing about them is that they can be written as a function of a sufficient number of independent variables to completely define the thermodynamic state of the system. Such a set is said to be a complete set. As it turns out, any thermodynamic system is completely defined when both the masses of all the substances within it are defined and two additional independent variables are fixed. This is Duhem’s theorem. From a real-life perspective, it is natural to choose pressure and temperature as those “independent variables” — physical quantities that we have a “feel” for and we think we can control — rather than specific volume or entropy. As we will see later, they are also convenient variables of choice because they are homogeneous of degree zero in mass.
Let “ ” be a given extensive property of a multi-component system. From the previous section, we know that the value of “ ” must be fixed and uniquely determined once we fix the pressure, temperature, and number of moles of each component in the system. This is,
Additionally, we recall that extensive properties are homogeneous of degree one with respect to number of moles and homogeneous of degree zero with respect to pressure and temperature. Thus, expression (15.6b) is readily applicable:
where we have just defined:
Equation (15.7c) is a very important definition. It defines the concept of a partial molar quantity. A partial molar quantity represents the change in the total quantity ( ) due to the addition of an infinitesimal amount of species “i” to the system at constant pressure and temperature. Euler’s theorem gave birth to the concept of partial molar quantity and provides the functional link between it (calculated for each component) and the total quantity. The selection of pressure and temperature in (15.7c) was not trivial. First, they are convenient variables to work with because we can measure them in the lab. But most important, they are intensive variables, homogeneous functions of degree zero in number of moles (and mass). This allowed us to use Euler’s theorem and jump to (15.7b), where only a summation with respect to number of moles survived. The definition of the partial molar quantity followed.
The conventional notation we are going to follow throughout the following section is:
= Total quantity (e.g., total volume, total internal energy, etc),
= Molar quantity, i.e., total quantity per unit mole:
= Partial molar quantity,
= Mass or specific quantity, i.e., total quantity per unit mass:
We can rewrite equation (15.7b) in terms of molar quantity using the definition in (15.8a),
where:
Any molar quantity in thermodynamics can be written in terms of the partial molar quantity of its constituents. If we set , we end up with,
Equivalently, if we set (total volume),
Notice that for single component systems (xi=1), partial molar properties are just equal to the molar property:
This is also a consequence of the definition in (15.7c),
For a pure component, and:
The reason for the introduction of the concept of a partial molar quantity is that often times we deal with mixtures rather than pure-component systems. The way to characterize the state of the mixtures is via partial molar properties. This concept provides the bridge between the thermodynamics of systems of constant composition, which we have studied so far, and the thermodynamics of systems of variable composition, which we will deal with in the next section. Basically, the definition in (15.7c):
allows us to quantify how the total, extensive property changes with additions of ni at constant pressure and temperature. If you look at (15.7b) and (15.9), you will also realize that (15.7c) is just an allocation formula that allows assigning to each species “i” a share of the total mixture property, such that:
We can play with “ ” a little more. Let us say that we are now interested in looking at the differential changes of . Since we also know that is a state function, and given the functional relationship in (15.7a), the total differential for is written:
or
Basically, equations (15.13) tell us that any change in P, T, or ni will cause a corresponding change in the total property, . This is a reinforcement of what is explicitly declared in (15.7a). If we recall (15.7b), an alternate expression for the total differential in (15.13) is written:
If we subtract (15.14) from (15.13b), we get:
Therefore,
Equation (15.16) is the well-known Gibbs-Duhem equation. It can be applied to any extensive thermodynamic property: U, S, H, G, A, and it must hold true. It represents a thermodynamic constraint between the intensive variables P, T and . Pressure, temperature and partial molar properties cannot vary in just any fashion; any change taking place among them must satisfy (15.16). The change in any one of them can be calculated as a function of the change in the other two by means of the Gibbs-Duhem equation. This equation is the basis for thermodynamic consistency checks of experimental data.
Thermodynamics of Systems of Variable Composition (Open Multicomponent Systems)
To extend all of the previous concepts to systems of variable mass, we must now consider at least one new variable: number of moles, n. To account for this effect, you will see below that we will have to introduce a “new” thermodynamic property. Let us take the case of the internal energy. For a constant composition system, we wrote:
and,
If this system has a single component, and now we allow its mass (and hence, number of moles, n) to change (an open system), the change in U (dU) is no longer just a function of dS and dV. We now have to account for changes in ‘n’, thus:
If we had a binary system, we would have two new variables, ‘n1’ and ‘n2’ (n=n1+n2) and we would have to expand (15.17) accordingly,
Hence, for a multi-component system, we just keep on adding terms ( ):
Thermodynamics defines this ‘coefficient’ which multiplies the change in the number of moles of each component (dni) as the ‘chemical potential’ of that component(μi). See how the chemical potential is a thermodynamic property that must be defined for the proper description of a system of variable composition — that is, an open system.
Then, we write:
and finally,
The same can be done with the thermodynamic definitions for dH, dG, and dA (the rest of equations 14.22). In fact, the chemical potential may be defined in at least four different and equivalent ways. You can now show that for equations (14.22) to account for systems of variable composition, we would have to expand them into:
Because thermodynamics defines the ‘coefficient’ which multiplies the change in the number of moles of each component (dni) as the ‘chemical potential’ of that component( ), we have three new ways to express it:
Don’t any of these three equations ring a bell? Don’t forgot the definition of (15.7c). Of all the four available definitions for chemical potential, there is one that suits our definition of a partial molar quantity perfectly. Compare equation (15.23b) to (15.7c). What we can say is that the chemical potential of a component “i” is equal to the partial molar Gibbs energy of such component:
Notice that, for a pure component, the chemical potential is equal to the molar Gibbs energy of the substance (see equation 15.9),
When we introduce the definition of chemical potential into each of equations (15.22), the fundamental thermodynamic expressions that apply to systems of variable composition become:
It is clear that equations (14.23) still hold — evaluated at constant “n” (total number of moles) — as shown:
The same reasoning applies to Maxwell’s relationships. From the above expressions, equation (15.22b) is the only one that matches equation (15.13). Notice that the following additional identities can be also identified (see equations 14.20):
We can see that chemical potential can be calculated by solving any of these differential expressions. To do this, experimental information is needed on how the other properties (T, V, S, P) change with additions of the given species (ni) under certain restraining conditions.
In some instances, we may have an open system of constant composition. This is the case of a system of a pure component exchanging mass with its surroundings. For such a system, nc = 1 and equations (15.26) are written as:
Equations (14.23) and (15.27) will still hold with .
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
For a design project involving a binary C1/C2 system, an engineer needs to know the partial molar volumes of C1 and C2 at the same conditions. Due to budget constraints, he was able to measure only one of them. Speculate on how to go about obtaining the second one.
Thermodynamic Tools (III)
Module Goals
Module Goal: To establish the mathematical framework for thermodynamics of phase equilibrium.
Module Objective: To establish that there is an unique relationship between partial molar quantities in any mixture.
The Chemical Potentials
We have just seen that the chemical potential is a thermodynamic property which is related to all thermodynamic properties with units of energy. Its most useful definition is given in terms of constant pressure and temperature:
This constitutes the working definition of chemical potential, the one that relates it to the partial molar quantity concept studied before.
Although the mathematical definition of chemical potential can be stated clearly, its “physical” meaning is not as easy to grasp. It is much easier to understand the physical implications of “pressure,” “temperature,” and “internal energy” than it is to undestand the physical interpretation of “chemical potential.” Given equation (15.24), and recognizing Gibbs free energy (G) as the capacity of a system to do work, we may write the following formal definition of chemical potential:
The chemical potential of a component in a given phase is the rate of increase of the capacity of the phase to do work per unit addition of the substance to the phase, at constant temperature and pressure.
We may also quote the definition that J.W. Gibbs provided for it:
If to any homogeneous mass, we suppose an infinitesimal quantity of any substance to be added, the mass remaining homogeneous and its entropy and volume remaining unchanged, the increase of energy of the mass divided by the quantity of the substance added is the potential for that substance in the mass considered.
This definition is closely related to the mathematical definition given in (15.20).
To understand the physical implications of the chemical potential of a species, we have to recall that for any thermodynamic process to be carried out, a driving force must be causing it. For instance, a pressure gradient is the driving force that causes the bulk movement of fluids from one point to the other, and a temperature gradient provides the potential difference needed for heat to flow. We also know that if we have a higher concentration of solute in a homogeneous system, it will diffuse to the zones of lower concentration. Here, the chemical potential is responsible for the diffusion of species within two points in space, or even its exchange between two different phases, without the presence of either pressure or temperature gradients. The chemical potential is the potential describing the ability of species to move from one phase to another.
The Thermodynamic Concept of Equilibrium
Intuitively, the concept of equilibrium conveys the message that something “balances out.” Equilibrium describes a state of vanishing driving forces or gradients, where everything remains as it is. If a system is in equilibrium, it retains its current state because there are no driving forces causing anything to change.
If two materials have the same temperature, we say that they are in thermal equilibrium. No exchange of heat takes places because there are no thermal gradients. For instance, a liquid and a vapor phase are in thermal equilibrium when:
We achieve mechanical equilibrium if two substances are found at the same pressure. No bulk movement of fluids takes place because there are no pressure gradients. A liquid and a vapor phase are in mechanical equilibrium when:
For a thermodynamic system to be in equilibrium, all intensive (temperature, pressure) and extensive thermodynamic properties (U, G, A, H, S, etc) must be constants. Hence, the total change in any of those properties ( ) must be zero at equilibrium.
Now we would like to have a concept of thermodynamic equilibrium for a vapor-liquid equilibrium. Let us consider a closed, heterogeneous vapor-liquid system. Any changes in a total property of the system will be the result of the changes of that property in the liquid phase plus the changes of that property in the vapor phase.
In this case, liquid and vapor by themselves are not closed systems; they can exchange matter between themselves but not with the surroundings. To elaborate more upon the concept of equilibrium, let’s look at equation (15.26c). Because it is written in terms of changes in pressure and temperature, two measurable laboratory quantities, it is the “friendliest” of all fundamental equations. We write it for both of the phases:
In (16.3), for , we get:
Hence,
Since at equilibrium all extensive properties, such as G, must remain constant, dG(total) must be zero. For this to hold true, and by inspection of equation (16.6), the conditions for thermodynamic equilibrium are:
It can be also proven that, at equilibrium, the total free energy of the system (G(total)) must take a minimum value; this reinforces the fact that dG(total)=0 at equilibrium. The minimum Gibbs energy criterion for equilibrium is a restatement of the second law of thermodynamics, from which we know that the entropy of a system in equilibrium must be at its maximum, considering all of the possible states for equilibrium.
It is somehow reasonable that for a true equilibrium condition there should be neither pressure nor temperature gradients (equations 16.7 and 16.8). This is because equilibrium is, at the very least, a state of lack of gradients. But what is equation (16.9) trying to tell us? To demystify equation (16.9), we recall that we are dealing with a closed system, hence, the total amount of moles per species:
must be constant (we do not allow for chemical reactions within the system). Thus we write:
Therefore,
(16.12) into (16.11) yields:
For equation (16.13) to hold true,
We have then arrived at the criteria for vapor-liquid equilibria for a system at constant pressure and temperature: the chemical potential of every species must be the same in both phases. We may generalize this finding to any number of phases, for which the chemical potential of every species must be the same in all phases. The chemical potential being the driving force which moves a species from one phase to the other, equation (16.14) is physically reasonable. If the chemical potential of a species in one phase is the same as that in the other, there is zero driving force and thus a zero net transfer of species at equilibrium.
Fugacity
We have seen that, for a closed system, the Gibbs energy is related to pressure and temperature as follows:
For a constant temperature process,
For an ideal gas,
This expression by itself is strictly applicable to ideal gases. However, Lewis, in 1905, suggested extending the applicability of this expression to all substances by defining a new thermodynamic property called fugacity, f, such that:
This definition implies that for ideal gases, ‘f’ must be equal to ‘P’. For mixtures, this expression is written as:
where are the partial molar Gibbs energy and fugacity of the i-th component, respectively. Fugacity can be readily related to chemical potential because of the one-to-one relationship of Gibbs energy to chemical potential, which we have discussed previously. Therefore, the definition of fugacity in terms of chemical potential becomes:
For a pure substance,
For a component in a mixture,
The fugacity coefficient ( ) is defined as the ratio of fugacity to its value at the ideal state. Hence, for pure substances:
and for a component in a mixture,
The fugacity coefficient takes a value of unity when the substance behaves like an ideal gas. Therefore, the fugacity coefficient is also regarded as a measure of non-ideality; the closer the value of the fugacity coefficient is to unity, the closer we are to the ideal state.
Fugacity turns out to be an auxiliary function to chemical potential. Even though the concept of thermodynamic equilibrium which we discussed in the previous section is given in terms of chemical potentials, above definitions allow us to restate the same principle in terms of fugacity. To do this, previous expressions can be integrated for the change of state from liquid to vapor at saturation conditions to obtain:
For equilibrium, ,hence,
Therefore:
For equilibrium, fugacities must be the same as well! This is, for a system to be in equilibrium, both the fugacity and the chemical potential of each component in each of the phases must be equal. Conditions (16.14) and (16.25) are equivalent. Once one of them is satisfied, the other is satisfied immediately. Using to describe equilibrium is a matter of choice, but generally the fugacity approach is preferred.
Expressions for Fugacity Calculation
It is clear that, if we want to take advantage of the fugacity criteria to perform equilibrium calculations, we need to have a means of calculating it. Let us develop a general expression for fugacity calculations. Let us begin with the definition of fugacity in terms of chemical potential for a pure component shown in (16.21a):
The Maxwell’s Relationships presented in equation (15.27c) is written for a pure component system as:
Consequently,
Substituting (16.28) into (16.26),
Introducing the concept of fugacity coefficient given in equation (16.23a),
We end up with:
or equivalently,
Integrating expression (16.31b),
It is convenient to define the lower limit of integration as the ideal state, for which the values of fugacity coefficient, volume, and compressibility factor are known.
At the ideal state, in the limit ,
Substituting into (16.32),
Equation (16.34) is the expression of fugacity coefficient as a function of pressure, temperature, and volume. Notice that this expression can be readily rewritten in terms of compressibility factor:
Let us also derive the expression for the fugacity coefficient for a component in a multicomponent mixture. Following a pattern similar to that which we have presented, beginning with the definition of fugacity for a component in terms of chemical potential:
This time, it is more convenient to use the Maxwell’s Relationships presented in equation (15.27d):
After you introduce the definitions of fugacity coefficient and compressibility factor:
and recalling that our lower limit of integration is the ideal state, for which, at the limit :
it can be proven that:
The multi-component mixture counterpart of equation (16.35) becomes:
where:
Equations (16.34), (16.35), (16.40), and (16.41) are very important for us. Basically, they show that fugacity, or the fugacity coefficient, is a function of pressure, temperature and volume:
This tells us that if we are able to come up with a PVT relationship for the volumetric behavior of a substance, we can calculate its fugacity by solving such expressions. It is becoming clear why we have studied equations of state — they are just what we need right now: PVT relationships for various substances. Once we have chosen the equation of state that we want to work with, we can calculate the fugacity of each component in the mixture by applying the above expression. Now that we know how to calculate fugacity, we are ready to apply the criteria for equilibrium that we just studied! That is the goal of the next module.
Cubic EOS Fugacity Expressions
Expressions (16.34) and (16.40) are particularly suitable for the calculation of fugacity with P-explicit equations of state, which cubic equations of state are. One can take every cubic EOS we have presented and proceed with the integration, coming up with the expression for fugacity for that particular equation of state. We will spare the reader these derivations. The fugacity expressions for the cubic EOS of most interest to us (SRK and PR EOS) are presented below:
SRK EOS
Pure Substance
Mixtures
PR EOS
Pure Substance
Mixtures
The expressions for are the same as given before in the previous modules. (AA)i and (BB)i are calculated as:
A and B parameters and the Z-factor of each phase are needed in order to calculate the corresponding fugacity coefficients. Now that we know how to calculate fugacity via EOS, and how this concept can be applied for equilibrium calculations (Section 16.2), we are ready to resume our discussion on Vapor-Liquid Equilibrium as we left it in Module 13. In our next module, we will concentrate on Vapor-Liquid Equilibrium via EOS.
Action Item
Answer the following problem, and submit your answer to the drop box in Canvas that has been created for this module.
Please note:
- Your answer must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
- Provide a short lay person definition of Chemical Potential and Fugacity. Explain how these variables can be used to describe phase equilibrium.
Vapor-Liquid Equilibrium via EOS
Module Goals
Module Goal: To use cubic equations of state for the description of phase equilibrium.
Module Objective: To integrate the knowledge of qualitative phase behavior and the framework for quantification to actually build a phase equilibrium model.
Introduction
Gas and liquid co-existence is common to all petroleum and natural gas applications, as we have mentioned already. Additionally, in our discussions presented in Modules 12 and 13, we tried to mathematically model the problem of vapor-liquid co-existence in equilibrium. As we recall, at that time we concluded that we were lacking tools necessary to complete the definition of the problem. Then we went on and concentrated on building those thermodynamic tools which we needed. Now we are ready to couple the concepts reviewed in Modules 14 through 16 (“Thermodynamic Tools”) with those reviewed in Modules 12 and 13. In order for us to do that, we will need to apply our knowledge of equations of state (studied in Modules 6 through 11).
Once the mathematics of vapor-liquid equilibrium is understood, we will be able to solve for a variety of applications. They will be discussed in the last modules of this course. One of those applications will be to generate any sort of phase diagrams, like the ones that we studied in our earlier discussions.
As you see, everything that we have studied in this course is completely interlinked. That’s one of the main ideas that I want you to glean from these discussions.
Equilibrium and Equilibrium Ratios (Ki)
Consider a liquid-vapor in equilibrium. As we have discussed previously, a condition for equilibrium is that the chemical potential of each component in both phases are equal, thus:
We showed that this is equivalent to:
This is, for a system to be in equilibrium, the fugacity of each component in each of the phases must be equal as well. The fugacity of a component in a mixture can be expressed in terms of the fugacity coefficient. Therefore, the fugacity of a component in either phase can be written as:
Introducing (17.3) into (17.2),
This equilibrium condition can be written in terms of the equilibrium ratio , to get:
Do you recall the problem at the end of Module 13? At that point we needed a more reliable way to calculate the equilibrium ratios that showed up in the Rachford-Rice objective function. We demonstrated that once we know all values of Ki’s, the problem of vapor-liquid equilibrium is reduced to solving the Rachford-Rice objective function, using the Newton-Raphson Procedure.
We can now calculate equilibrium ratios, using (17.5), in terms of fugacity coefficients. We also know that we have an analytic expression for the calculation of fugacity coefficients via EOS — this was shown in the last section of the previous module. This is why we call this module “Vapor Liquid Equilibrium via EOS.”
Is this the end to our problems? Not quite. Take a look at the expression for fugacity coefficients in mixtures both for SRK EOS and PR EOS. It is clear that they are functions of the pressure, temperature, and composition of the phases:
Do we know the composition of the phases “xi”, “yi” in advance? In a typical flash problem, we are given pressure, temperature and overall composition (zi). What do we want to know? How much gas, how much liquid, and the compositions of the phases: . So, we do not know those compositions in advance; therefore, as it stands, we cannot calculate (17.6) or (17.5). Thus far, it seems that the flash problem is unsolvable.
If we are bold enough, we could try to overcome this problem by “guessing” those compositions, and proceed by solving (17.6) and (17.5). With this “rough” estimate for Ki’s, we could solve for “ ” with the procedure outlined in Module 13 (“Objective Function and Newton-Raphson Procedure”). Once “” is known, we could back calculate the compositions of the phases using equations (12.7) and (12.11). If we were correct, those compositions would match each other (the “guessed” ones with respect to the “back-calculated”). More than likely, this would not happen, and we would have to make a new “guess.” This is, fundamentally, an iterative procedure. Although this is not what we do, it does illustrate that this problem is solvable by implementing the appropriate iterative scheme.
In equations (17.4) and (17.5), the fugacity of the liquid and vapor phases were computed in terms of the fugacity coefficient. Hence, this method of expressing the equilibrium criteria is known as the dual-fugacity coefficient method. For the sake of completeness, it is necessary to indicate that the fugacity of a component in a mixture can also be expressed in terms of a thermodynamic concept called the activity coefficient. While the fugacity coefficient is seen as a measure of the deviation of behavior with respect to the ideal gas model, the activity coefficient measures the deviation of behavior with respect to the ideal liquid model. This approach is called the dual-activity coefficient method, in which both liquid and vapor phase fugacities are expressed in terms of the activity coefficient and substituted into the equilibrium criteria in (17.2). A mixed activity coefficient-fugacity coefficient method can be also devised by expressing the liquid phase fugacities in terms of activity coefficients and the vapor phase fugacities in terms of fugacity coefficients. Each of the aforementioned methods for the calculation of phase equilibria has its advantages and disadvantages. The dual-fugacity-coefficient method is simpler both conceptually and computationally, but if the equation of state does not predict liquid and vapor densities well, the results may be inaccurate. The activity coefficient method can be more accurate, but it is more complicated to implement. For the rest of the discussion, the dual-fugacity coefficient approach will be used.
Solution Algorithms for VLE Problems
We have essentially reduced the typical VLE problem to that of solving a system of non-linear algebraic equations. The objective function is the nucleus of the VLE calculation. Rather than solve the material balance equations in their elemental form, the use of an objective function will allow for a more stable iteration scheme. We have seen that three objective functions are available for this calculation:
Expression (17.7c) is the Rachford-Rice Objective Function; we have proven that its numerical solution is cleaner than that of equations (17.7a) and (17.7b). We also discussed that the key problem in solving for “” is the need for values for the equilibrium ratios (Ki’s). With the aid of equations (17.5) and (17.6) these problems can be solved simultaneously by iteration techniques.
In the problem we have posed, we have (3n+1) unknowns:
And,
And we also have (3n+1) equations:
where P, T, and zi are the values that we know. See how this is only a restatement of the original set of equations that contain the equilibrium conditions, material balances, and molar fraction constraints:
Since we have the same number of equations as unknowns, this system is determined and has a unique solution. To solve this system of simultaneous non-linear equations, there are two categories of solution techniques:
- Newton-type methods,
- Substitution-type methods.
Newton-type methods for more than one unknown require finding (n x n) elements of a Jacobian matrix at every iteration step. This could be computationally expensive. Additionally, the Newton Raphson method requires a very good initial guess (i.e., close to the actual solution) to guarantee convergence to the true values. This is not always possible, especially at the start of the procedure.
The most popular method, and the easiest to implement, is the substitution type. However, substitution type methods can be quite slow for some conditions of interest. In these sort of cases, we either switch to a Newton-Raphson solver (that has a much better rate of convergence) or implement an acceleration procedure to the substitution method itself.
Successive Substitution Method (SSM)
In a substitution-type method, we start with initial guesses for all of the unknowns and loop around the equations to obtain “better” approximations for each of them. We test the goodness of the solution at every time step by comparing the new, better approximation to the previous guess. If the correction is small under certain convergence criteria, the procedure is stopped and we use the results from the last iteration as the final answer.
As we discussed in the previous section, reliable values for the equilibrium constants (Ki’s) must be obtained before we can solve the Rachford-Rice Objective Function. Generally, first estimates for equilibrium constants are calculated by using Wilson’s empirical equation (equation 13.15). However, Wilson’s correlation yields only approximate values for equilibrium ratios. Here, we apply thermodynamic equilibrium considerations in order to obtain more reliable predictions for Ki’s.
Let us recall that for a system to be in equilibrium, any net transfer (of heat, momentum, or mass) must be zero. For this to be true, all potentials (temperature, pressure, and chemical potential) must be the same in all of the phases. Provided that the temperature and pressure of both phases are the same, a zero net transfer for all components in the mixture results when all chemical potentials are the same. A restatement of this: all fugacities for all components in each phase are equal. Since fugacity is a measure of the potential for transfer of a component between two phases, equal fugacities of a component in both phases results in zero net transfer. SSM (Successive Substitution Method) takes advantage of this fact. Equation (17.5) showed that the fugacity criterion for equilibrium allows writing the equilibrium ratios Ki as a function of fugacity coefficients as follows:
Equation (17.10) presupposes equality of fugacity (), but during an iterative procedure, fugacities may not be equal () until convergence conditions have been attained. Therefore, if fugacities are not equal (convergence has not been achieved), equation (17.10) becomes:
Using the above equation, a correction step can be formulated to improve the current values of Ki. The SSM-updating step is written as:
SSM updates all previous equilibrium ratios (Ki) using the fugacities predicted by the equation of state. This iteration method requires an initial estimation of Ki-values — for which Wilson’s correlation is used. It can easily be concluded that the convergence criteria will be satisfied whenever the fugacity ratios of all the components in the system are close to unity. Such condition is achieved when the following inequality is satisfied:
The Accelerated Successive Substitution Method (ASSM)
When the system is close to the critical point and fugacities are strongly composition-dependent, a slowing-down of the convergence rate of the SSM (Successive Substitution Method) is to be expected. In an attempt to avoid slow convergence problems, some methods have been proposed. Among the most popular are the Minimum Variable Newton Raphson (MVNR) Method and the Accelerated and Stabilized Successive Substitution Method (ASSM).
The ASSM is basically an accelerated version of the SSM procedure, and thus follows a similar theory. Such procedure is implemented to accelerate the calculation of Ki-values, especially in the region close to critical point where the use of the SSM alone will not be efficient. The ASSM technique was presented by Rinses et al. (1981) and consists of the following steps:
- Use the SSM technique to initiate the updating of the Ki-values the first time.
- Check all following criteria at every step during iterations using the SSM:
(17.13a)(17.13b)(17.13c)(17.13d)
These criteria show that you have sufficient proximity to the conditions to ensure the efficiency of the method. Rri is the ratio of liquid fugacity to gas fugacity of the i-th component and ‘’ is molar gas fraction of the two-phase system.
(17.14) -
If the system satisfies ALL above criteria, the iteration technique is then switched from the SSM to the ASSM. Otherwise, SSM is used for the update of the Ki-values. The following expressions are used to update Ki-values in ASSM:
where
In some cases, using a constant acceleration value of is good enough.
- Once all the criteria in step (2) are satisfied, skip step (2) for the subsequent iterations and use the ASSM technique to update Ki-values until convergence is attained, unless it does not give acceptable new estimates (as stated next).
- When ASSM is used, it must always be tested to show that it leads to an improved solution (i.e., that it brings fugacity ratios closer to unity). If not, it must be rejected and switched back to SSM.
Even though we are outlining Risnes et al.’s version of the accelerated Successive Substitution Method, there are several other published algorithms whose main purpose have also been to accelerate the successive substitution method. Fussel and Yanosik (1978), Michelsen (1982), and Mehra et al. (1983) are examples of such attempts. Risnes et al. version is the easiest and most straightforward to implement, but it is subjected to limitations.
The Stability Criteria
Interestingly enough, one of the most difficult aspects of making VLE calculations may not be the two-phase splitting calculation itself, but knowing whether or not a mixture will actually split into two (or even more) phases for a pressure and temperature condition.
A single-phase detection routine has to be simultaneously introduced at this stage to detect whether the system is in a true single-phase condition at the given pressure and temperature or whether it will actually split into two-phases. Several approaches may be used here: the Bring-Back technique outlined by Risnes et al. (1981), and Phase Stability Criteria introduced by Michelsen (1982), among others. Here we describe Michelsen’s stability test.
Michelsen (1982) suggested creating a second-phase inside any given mixture to verify whether such a system is stable or not. It is the same idea behind the Bring-Back procedure (Risnes et al., 1981), but this test additionally provides straightforward interpretation for the cases where trivial solutions are found
(Ki’s —> 1). The test must be performed in two parts, considering two possibilities: the second phase can be either vapor-like or liquid-like. The outline of the method is described below, following the approach presented by Whitson and Brule (2000).
- Calculate the mixture fugacity (fzi) using overall composition zi.
- Create a vapor-like second phase,
- Use Wilson’s correlation to obtain initial Ki-values.
- Calculate second-phase mole numbers, Yi:
(17.15)
- Obtain the sum of the mole numbers,
(17.16)
- Normalize the second-phase mole numbers to get mole fractions:
(17.17)
- Calculate the second-phase fugacity (fyi) using the corresponding EOS and the previous composition.
- Calculate corrections for the K-values:
(17.18)(17.19) - Check if:
- Convergence is achieved:
(17.20)
- A trivial solution is approached:
(17.21)
If a trivial solution is approached, stop the procedure.
If convergence has not been attained, use the new K-values and go back to step (b).
- Convergence is achieved:
-
Create a liquid-like second phase,
Follow the previous steps by replacing equations (17.15), (17.16), (17.17), and (17.18) by (17.22), (17.23), (17.24), and (17.25) respectively.
(17.22)(17.23)(17.24)(17.25)
The interpretation of the results of this method follows:
- The mixture is stable (single-phase condition prevails) if:
- Both tests yield S < 1 (SL < 1 and SV < 1),
- Or both tests converge to trivial solution,
- Or one test converges to trivial solution and the other gives S < 1.
- Only one test indicating S > 1 is sufficient to determine that the mixture is unstable and that the two-phase condition prevails. The same conclusion is made if both tests give S > 1, or if one of the tests converges to the trivial solution and the other gives S > 1.
Action Item
Answer the following problem, and submit your answer to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
- Provide a comprehensive flowchart of how to build a flash calculation model for a multi-component mixture. Assume that the data you have available is pressure, temperature, fluid composition, and all the properties of the pure components making up the mixture. This flowchart should be clear enough so that anyone could code it and generate results!
Properties of Natural Gas and Condensates (I)
Module Goals
Module Goal: To highlight the important properties used to characterize natural gas and condensate systems.
Module Objective: To present the most popular models for estimating properties of natural gas and condensate systems.
Introduction
Fluid properties are used to characterize the condition of a fluid at a given state. A reliable estimation and description of the properties of hydrocarbon mixtures is fundamental in petroleum and natural engineering analysis and design. Fluid properties are not independent, just as pressure, temperature, and volume are not independent of each other. Equations of State provide the means for the estimation of the P-V-T relationship, and from them many other thermodynamic properties can be derived. Compositions are usually required for the calculation of the properties of each phase. For a VLE system, using the tools we have discussed in the previous lectures, we are ready to predict some important properties of both the liquid (condensate) and vapor (natural gas) phases — by means of the known values of composition of both phases. Some of the most relevant are discussed next.
Molecular Weight
The molecular weight (MW) of each of the phases in a VLE system is calculated as a function of the molecular weight of the individual components (MWi), provided that both the composition of the gas (yi) and the liquid (xi) are known:
Density
Density is customarily defined as the amount of mass contained in a unit volume of fluid. Density is the single-most important property of a fluid, once we realize that most other properties can be obtained or related to density. Both specific volume and density — which are inversely proportionally related to each other — tell us the story of how far apart the molecules in a fluid are from each other. For liquids, density is high — which translates to a very high molecular concentration and short intermolecular distances. For gases, density is low — which translates to low molecular concentrations large intermolecular distances.
The question then is: Given this, how can we obtain this all-important property called density? This takes us back to Equations of State (EOS). Since very early times, there have been correlations for the estimation of density of the liquids (oil, condensates) and gases/vapors (dry gases, wet gases). In modern times, equations of state (EOS) are a natural way of obtaining densities. The density of the fluid ‘f’ is calculated using its compressibility factor (Zf) as predicted by an appropriate equation of state. From the real gas law, the density can be expressed as:
where: MWf is the molecular weight of fluid ‘f’. Expression (18.2) is used for both the gas and liquid density. In either case, the proper value for MWf (either MWg or MWl) and Zf (either Zg or Zo) has to be used. This takes us back to the discussion of equations of state. From Equation (18.2) it is clear that all that we need is the Z-factor.
The all-important parameter to calculate density is the Z-factor, both for the liquid and vapor phases. The relation between liquid behavior and Z-factor is not obvious, because Z-factor has been traditionally defined for gases. However, we can get “Z” for liquids. “Z” is, indeed, a measure of departure from the ideal gas behavior. Fair enough, for defining “Z” for liquids, we still measure the departure of liquid behavior from ideal gas behavior. A “liquid state” is a tremendous departure from ideal-gas conditions, and as such, “Z” for a liquid is always very far from unity. Typical values of “Z” for liquids are small.
Equations of State have proven very reliable for the estimation of vapor densities, but they do not do as good a job for liquid densities. There is actually a debate among different authors about the reliability of Z-factor estimations for liquids using EOS. In fact, people still believe the EOS are not reliable for liquid density predictions and that we should use correlations instead. However, Peng-Robinson EOS provides fair estimates for vapor and liquid densities as long as we are dealing with natural gas and condensate systems.
Empirical correlations for Z-factor for natural gases were developed before the advent of digital computers. Although their use is in decline, they can still be used for fast estimates of the Z-factor. The most popular of such correlations include those of Hall-Yarboroug and Dranchuk-Abou-Kassem.
Chart look-up is another means of determining Z-factor of natural gas mixtures. These methods are invariably based on some type of corresponding states development. According to the theory of corresponding states, substances at corresponding states will exhibit the same behavior (and hence the same Z-factor). The chart of Standing and Katz is the most commonly used Z-factor chart for natural gas mixtures.
Methods of direct calculation using corresponding states have also been developed, ranging from correlations of chart values to sophisticated equation sets based on theoretical developments.
However, the use of equations of state to determine Z-factors has grown in popularity as computing capabilities have improved. Equations of state represent the most complex method of calculating Z-factor, but also the most accurate. A variety of equations of state have been developed to describe gas mixtures, ranging from the ideal EOS (which yields only one root for the vapor and poor predictions at high pressures and low temperatures), cubic EOS (which yields up to three roots, including one for the liquid phase), and more advanced EOS such as BWR and AGA8.
References:
Hall K., and Yarborough, L. (1973), “A New Equation of State for Z-factor Calculations”, Oil and Gas Journal, June 1973, pp. 82-92.
Dranchuk, P. and Abou-Kassem, J. (1975), “Calculation of Z-factors for Natural Gases Using Equations-of-State”, JCPT, July-September 1975, p. 34-36.
Standing, M. and Katz, D. (1942), “Density of Natural Gases”, Trans. AIME, v. 146, pp. 140-149.
Specific Gravity
Specific gravity is defined as the ratio of fluid density to the density of a reference substance, both defined at the same pressure and temperature. These densities are usually defined at standard conditions (14.7 psia and 60°F). For a condensate, oil or a liquid, the reference substance is water:
The value of water density at standard conditions is 62.4 lbm/ft3 approximately. For a natural gas, or any other gas for this matter, the reference substance is air:
Or, equivalently, substituting Equation (18.2) evaluated at standard conditions ( for most gases),
where the value of the molecular weight for air is MWair = 28.96 lbm/lbmol. Specific gravity is nondimensional because both numerator and denominator have the same units.
API
Petroleum and Natural Gas Engineers also use another gravity term which is called API gravity. It is used for liquids (e.g., condensates) and is defined as:
By definition (see Equation 18.3), the specific gravity of water is unity. Therefore, water has an API gravity of 10. The API gravity of 10 is associated with very heavy, almost asphaltic, oils. Light crude oils have an API greater than or equal to 45°. Condensate gravities range between 50° and 70° API. Liquid condensates are normally light in color.
Volumetric Factors (Bo and Bg)
Due to the dramatically different conditions prevailing at the reservoir when compared to the conditions at the surface, we do not expect that 1 barrel of fluid at reservoir conditions could contain the same amount of matter as 1 barrel of fluid at surface conditions. Volumetric factors were introduced in petroleum and natural gas calculations in order to readily relate the volume of fluids that are obtained at the surface (stock tank) to the volume that the fluid actually occupied when it was compressed in the reservoir.
For example, the volume that a live oil occupies at the reservoir is more than the volume of oil that leaves the stock tank at the surface. This may be counter-intuitive. However, this is a result of the evolution of gas from oil as pressure decreases from reservoir pressure to surface pressure. If an oil had no gas in solution (i.e., a dead oil), the volume that it would occupy at reservoir conditions is less than the volume that it occupies at the surface. In this case, only liquid compressibility plays a role in the change of volume.
The formation volume factor of a natural gas (Bg) relates the volume of 1 lbmol of gas at reservoir conditions to the volume of the same lbmol of gas at standard conditions, as follows:
Those volumes are, evidently, the specific molar volumes of the gas at the given conditions. The reciprocal of the specific molar volume is the molar density, and thus, Equation (18.5) could be written:
Introducing the definition for densities in terms of compressibility factor,
Therefore, recalling that ,
Gas formation volume factors can be also expressed in terms of [RB/SCF]. In such a case, 1 RB = 5.615 RCF and we write:
The formation volume factor of an oil or condensate (Bo) relates the volume of 1 lbmol of liquid at reservoir conditions to the volume of that liquid once it has gone through the surface separation facility.
The total volume occupied by 1 lbmol of liquid at reservoir conditions (Vo)res can be calculated through the compressibility factor of that liquid, as follows:
Upon separation, some gas is going to be taken out of the liquid stream feeding the surface facility. Let us call “nst” the moles of liquid leaving the stock tank per mole of feed entering the separation facility. The volume that 1 lbmol of reservoir liquid is going to occupy after going through the separation facility is given by:
Here we assume that the last stage of separation, the stock tank, operates at standard conditions. Introducing Equations (18.12) and (18.11) into (18.10), we end up with:
or,
Please notice that (Zo)sc — unlike Zsc for a gas — is never equal to one. Oil formation volume factor can be also seen as the volume of reservoir fluid required to produce one barrel of oil in the stock tank.
Isothermal Compressibilities
The isothermal compressibility of a fluid is defined as follows:
This expression can be also given in term of fluid density, as follows:
For liquids, the value of isothermal compressibility is very small because a unitary change in pressure causes a very small change in volume for a liquid. In fact, for slightly compressible liquid, the value of compressibility (co) is usually assumed independent of pressure. Therefore, for small ranges of pressure across which co is nearly constant, Equation (18.16) can be integrated to get:
In such a case, the following expression can be derived to relate two different liquid densities at two different pressures (p, pb):
The Vasquez-Beggs correlation is the most commonly used relationship for co.
For natural gases, isothermal compressibility varies significantly with pressure. By introducing the real gas law into Equation (18.16), it is easy to prove that, for gases:
Note that for an ideal gas, cg is just the reciprocal of the pressure. “cg” can be readily calculated by graphical means (chart of Z versus P) or by introducing an equation of state into Equation (18.19).
Surface Tension
Surface tension is a measure of the surface free energy of liquids, i.e., the extent of energy stored at the surface of liquids. Although it is also known as interfacial force or interfacial tension, the name surface tension is usually used in systems where the liquid is in contact with gas.
Qualitatively, it is described as the force acting on the surface of a liquid that tends to minimize the area of its surface, resulting in liquids forming droplets with spherical shape, for instance. Quantitatively, since its dimension is of force over length (lbf/ft in English units), it is expressed as the force (in lbf) required to break a film of 1 ft of length. Equivalently, it may be restated as being the amount of surface energy (in lbf-ft) per square feet.
Katz et al. (1959) presented the Macleod-Sudgen equation for surface tension () calculations in dynes/cm for hydrocarbon mixtures:
where:
Pchi = Parachor of component “i”,
xi = mole fraction of component “i” in the liquid phase,
yi = mole fraction of component “i” in the gas phase.
In order to express surface tension in field units (lbf/ft), multiply the surface tension in (dynes/cm) by 6.852177x10-3. The parachor is a temperature independent parameter that is calculated experimentally. Parachors for pure substances have been presented by Weinaug and Katz (1943) and are listed in Table 18.1.
| Component | Parachor |
|---|---|
| CO2 | 78.0 |
| N2 | 41.0 |
| C1 | 77.0 |
| C2 | 108.0 |
| C3 | 150.3 |
| iC4 | 181.5 |
| nC4 | 189.9 |
| iC5 | 225.0 |
| nC5 | 231.5 |
| nC6 | 271.0 |
| nC7 | 312.5 |
| nC8 | 351.5 |
Weinaug and Katz (1943) also presented the following empirical relationship for the parachor of hydrocarbons in terms of their molecular weight:
- This correlation may be used for pseudo-components or for those hydrocarbons not shown in Table 18.1.
Action Item
Answer the following problem, and submit your answer to the drop box in Canvas that has been created for this module.
Please note:
- Your answer must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
- Which of all the properties we have studied so far would you use to compare and distinguish among wet natural gas, dry natural gas, and gas-condensate systems? Explain why.
Properties of Natural Gas and Condensates (II)
Module Goals
Module Goal: To highlight the important properties used to characterize natural gas and condensate systems.
Module Objective: To present the most popular models for estimating properties of natural gas and condensate systems.
Heat Capacities
The constant volume heat capacity is defined by:
To see the physical significance of the constant volume heat capacity, let us consider a 1 lbmol of gas within a rigid-wall (constant volume) container. Heat is added to the system through the walls of the container and the gas temperature rises. It is evident that the temperature rise ( ) is proportional to the amount of heat added,
Introducing a constant of proportionality “cv”,
In our experiment, no work was done because the boundaries (walls) of the system remained unchanged. Applying the first law of thermodynamics to this closed system, we have:
Therefore, for infinitesimal changes,
As we have seen, constant volume heat capacity is the amount of heat required to raise the temperature of a gas by one degree while retaining its volume.
Let us now consider the same 1 lbmol of gas confined in a piston-cylinder equipment (i.e., a system with non-rigid walls or boundaries). When heat is added to the system, the gas temperature rises and the gas expands so that the pressure in the system remains the same at any time. The piston displaces a volume V and the gas increases its temperature in T degrees. Again, the temperature rise (T) is proportional to the amount of heat added, and the new constant of proportionality we use here is “cp”,
This time, some work was done because the boundaries (walls) of the system changed from their original position. Applying the first law of thermodynamics to this closed system, we have that:
If the pressure remained the same both inside and outside the container, the system made some work against the surroundings in the amount of . Introducing (19.7) into (19.6),
The left hand side of this equation represents the definition of enthalpy change ( ) for a constant-pressure process. Therefore:
Finally, for infinitesimal changes,
The function “cp” is called the constant pressure heat capacity. The constant pressure heat capacity is the amount of heat required to raise the temperature of a gas by one degree while retaining its pressure.
The units of both heat capacities are (Btu/lbmol-°F) and (cal/gr-°C). Their values are never equal to each other, not even for ideal gases. In fact, the ratio “cp/cv” of a gas is known as “k” — the heat capacity ratio — and it is never equal to unity. This ratio is frequently used in gas-dynamics studies.
Heat capacities can be calculated using equations of state. For instance, Peng and Robinson (1976) presented an expression for the departure enthalpy of a fluid mixture, shown below:
The value of the enthalpy of the fluid (H) is obtained by adding up this enthalpy of departure (shown above) to the ideal gas enthalpy (H*). Ideal enthalpies are sole functions of temperature. For hydrocarbons, Passut and Danner (1972) developed correlations for ideal gas properties such as enthalpy, heat capacity and entropy as a function of temperature. Therefore, an analytical relationship for “cp” can be derived taking the derivative of (19.12), as shown below:
where:
= ideal gas CP,
also found in the work of Passut and Danner (1972).
The second derivative of with respect to temperature can be calculated through the expression:
where,
For the evaluation of expression (19.13), the derivative of the compressibility factor with respect to temperature is also required. Using the cubic version of Peng-Robinson EOS, this derivative can be written as:
where,
“cp” and “cv” values are thermodynamically related. It can be proven that this relationship is controlled by the P-V-T behavior of the substances through the relationship:
For ideal gases, and Equation (18.28) collapses to:
Joule-Thomson Coefficient
One remarkable difference between flow of condensate (or liquid) and natural gases through a pipeline is that of the effect of pressure drop on temperature changes along the pipeline. This is especially true when heat losses to the environment do not control these temperature variations. Natural gas pipelines usually cool with distance (effect commonly called ‘Joule–Thomson cooling’), while oil lines heat. The reason for such dissimilarity pertains to the different effect that pressure drop has on the entropy of a natural gas than on the entropy of an oil mixture. Katz (1972) and Katz and Lee (1990) presented a very enlightening discussion on this regard.
Whether or not a gas cools upon expansion or compression — that is, when subjected to pressure changes — depends on the value of its Joule–Thomson coefficient. This is not only important for natural gas pipeline flow, but also for the recovery of condensate from wet natural gases. In the cryogenic industry, turboexpanders are used to subject a wet gas to a sudden expansion (sharp pressure drop) in order to cool the gas stream beyond its dew point and recover the liquid dropout.
Thermodynamically, the Joule–Thomson coefficient is defined as the isenthalpic change in temperature in a fluid caused by a unitary pressure drop, as shown:
Using thermodynamic relationships, alternative expressions can be written. For example, using the cycling rule we may write:
or,
We have also seen that we can express enthalpy changes in terms of pressure, temperature and volume changes:
Additionally, the following identity can be derived:
All together, we have several ways of calculating the Joule–Thompson coefficient for a fluid, as shown next:
Once the constant pressure specific heat “cp” is calculated as discussed in the previous lecture, all the entries in the previous expression are known and the Joule–Thomson coefficient can be analytically calculated. An interesting observation from all above expressions for “ ” is that the Joule–Thompson coefficient of an ideal gas is identically equal to zero. However, real fluids take positive or negative Joule–Thompson values.
Viscosity
What other properties are we interested in? We are interested in flow properties. Whether you are interested in flow in pipes or in porous media, one of the most important transport properties is viscosity. Fluid viscosity is a measure of its internal resistance to flow. The most commonly used unit of viscosity is the centi-poise, which is related to other units as follows:
1 cp = 0.01 poise = 0.000672 lbm/ft-s = 0.001 Pa-s
Natural gas viscosity is usually expected to increase both with pressure and temperature. A number of methods have been developed to calculate gas viscosity. The method of Lee, Gonzalez and Eakin is a simple relation which gives quite accurate results for typical natural gas mixtures with low non-hydrocarbon content. Lee, Gonzalez and Eakin (1966) presented the following correlation for the calculation of the viscosity of a natural gas:
where:
In this expression, temperature is given in (°R), the density of the fluid ( ) in lbm/ft3 (calculated at the pressure and temperature of the system), and the resulting viscosity is expressed in centipoises (cp).
The most commonly used oil viscosity correlations are those of Beggs-Robinson and Vasquez-Beggs. Corrections must be applied for under-saturated systems and for systems where dissolved gas is present in the oil. However, in compositional simulation, where both gas and condensate compositions are known at every point of the reservoir, it is customary to calculate condensate viscosity using Lohrenz, Bray & Clark correlation. It this type of simulation, it is usual to calculate gas viscosities based on Lohrenz, Bray & Clark correlation as well. This serves the purpose of guaranteeing that the gas phase and condensate phase converge to the same value of viscosity as they approach near-critical conditions.
Lohrenz, Bray and Clark (1964) proposed an empirical correlation for the prediction of the viscosity of a liquid hydrocarbon mixture from its composition. Such expression, originally proposed by Jossi, Stiel and Thodos (1962) for the prediction of the viscosity of dense-gas mixtures, is given below:
where:
= fluid viscosity (cp),
= viscosity at atmospheric pressure (cp),
= mixture viscosity parameter (cp-1),
= reduced liquid density (unitless),
Lohrenz et al. original paper presents a typographical error in Equation (19.26). Here it is written as originally proposed by Jossi, Stiel and Thodos (1962). All four parameters listed above have to be calculated as a function of critical properties in order to apply Equation (19.26). Lohrenz et al. original paper uses scientific units, here we present the equivalent equations in field (English) units.
For the viscosity of the mixture at atmospheric pressure ( ), Lohrenz et al. suggested using the following Herning & Zipperer equation:
where:
zj = mole composition of the i-th component in the mixture,
MWi = molecular weight of the i-th component (lbm/lbmol)
= viscosity of the i-th component at low pressure (cp):
[ if Tri ≤ 1.5 ]
[ if Tri > 1.5
where:
Tri = reduced temperature for the i-th component (T/Tci),
MWi = viscosity parameter of the i-th component, given by:
For the mixture viscosity parameter ( ), Lohrenz et al. applied an equivalent expression to that shown above but using pseudo-properties for the mixture:
where:
Tpc = pseudocritical temperature (oR),
Ppc = pseudocritical pressure (psia),
MWl = liquid mixture molecular weight (lbm/lbmol).
The reduced density of the liquid mixture ( ) is calculated as:
= mixture pseudocritical density (lbm/ft3),
Vpc = mixture pseudocritical molar volume (ft3/lbmol),
All mixture pseudocritical properties are calculated using Kay’s mixing rule, as shown:
“zi” pertains to the fluid molar composition, Tci is given in oR, Pci in psia, and Vci in ft3/lbmol. When the critical volumes are known in a mass basis (ft3/lbm), each of them is to be multiplied by the corresponding molecular weight. In the case of lumped C7+ heavy fractions, Lorentz et al. (1969) presented a correlation for the estimation C7+ critical volumes.
References:
Lee, A., Gonzalez, M., Eakin, B. (1966), “The Viscosity of Natural Gases”, SPE Paper 1340, Journal of Petroleum Technology, vol. 18, p. 997-1000.
Lohrenz, J., Bray, B.G., Clark, C.R. (1964), “Calculating Viscosities of Reservoir Fluids from their compositions”, SPE Paper 915, Journal of Petroleum Technology, p. 1171-1176.
Action Item
Answer the following problem, and submit your answer to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
- Gas metering is a most important activity in the natural gas business. Among the properties we have studied, which one would you emphasize in terms of accuracy for most common gas meters?
Engineering Applications (I)
Module Goals
Module Goal: To highlight some of the important applications of phase behavior in production operations.
Module Objective: To describe the use of flash calculations in separator optimization and gas-condensate reservoir description.
Introduction: Phase Behavior as the Quintessential Tool
Optimal design and the safe and efficient operation of hydrocarbon production handling and processing systems strongly depends on accurate knowledge of fluid phase behavior. In fact, in contrast with other disciplines, the practice of petroleum and natural gas engineering centers around understanding the interaction between fluids and various environments, including the reservoir, pipeline, separator, pumps and compressors, etc. Another distinguishing characteristic is the complexity of the fluid involved here — petroleum. Whereas, for instance, mechanical engineers deal mainly with water (single-component system) and air (considered ideal for most applications), here we are dealing with complex hydrocarbon mixtures where the composition dependence of thermophysical properties is very strong.
Another complication is the wide range of pressures and temperatures associated with the processes of interest, from ultralow temperatures (LNG) to as much as 210 °F and pressures ranging from atmospheric to several thousand psia. Within these ranges, the fluid can transcend the three principal phases, namely gas, liquid, and solid, and worse yet, any combination of these.
The combination of the complex mixtures involved, the wide compositional variability from reservoir to reservoir, from system to system, and the wide range of pressures and temperatures to which systems are often subjected (e.g. a pipeline) make the phase behavior of these systems a very challenging undertaking. Unless one has a good descriptive and predictive understanding of the fluid’s phase behavior, their interactions and responses cannot be successfully described.
In these last two modules of the course, we will examine some of the applications of our current knowledge of phase behavior and thermodynamics in Petroleum and Natural Gas Engineering. The message we would like to provide is very simple: the phase behavior of the hydrocarbon system must be fully grasped in order to fully understand the responses of condensate and natural gas systems and optimize their performance. For example, maximization of condensate yield is virtually impossible without the tools for accurate prediction of just how much liquid will exist under given conditions of pressure, temperature and composition. Therefore, having advanced predictive tools for the characterization of hydrocarbon phase behavior with the highest accuracy possible is the key to mastering the economics of hydrocarbon systems. In the next sections, we will explore some specific areas where the mastering of phase behavior concepts is a must.
Design and Optimization of Separators
Once oil and gas are brought to the surface, our main goal becomes that of transportation of the oil and gas from the wellhead to the refinery (for final processing). All equipment and processes required to accomplish this are found at the surface production facility. Hence, all surface production starts right at the wellhead. Starting at the wellhead, the complex mixture of produced fluids makes its way from the production tubing into the flow line. Normally, many wells are drilled to effectively produce the hydrocarbons contained in the field. From each of these wells emerge one or more flow lines depending on how many layers are being produced simultaneously. Depending on the physical terrain of the area and several other environmental factors, each of the flow lines may be allowed to continue from the wellhead to a central processing facility commonly referred as a production platform or a flow station, which then carries the fluids to the production platform. The combination of the wellhead, the flow lines, bulk headers, valves and fittings needed to collect and transport the produced fluid to the production platform is referred to as the gathering system.
The gathered fluids must be processed to enhance their value. First of all, fluids must be separated into their main phasial components - namely, oil, water, and natural gas. The separation system performs this function. For this, the system is usually made up of a free water knock-out (FWKO), flow line heater, and oil-gas (two-phase) separators. We will be looking at the design of this last component.
The physical separation of these three phases is carried out in several steps. Water is separated first from the hydrocarbon mixture (by means of the FWKO), and then the hydrocarbon mixture is separated into two hydrocarbon phases (gas and oil/condensate). A successful hydrocarbon separation maximizes production of condensate or oil, and enhances its properties. In field applications, this is accomplished by means of stage separation. Stage separation of oil and gas is carried out with a series of separators operating at consecutively reduced pressures. Liquid is discharged from a higher-pressure separator into the next-lower-pressure separator. The purpose of stage separation is to obtain maximum recovery of liquid hydrocarbons from the fluids coming from the wellheads and to provide maximum stabilization of both the liquid and gas effluents.
Surface Production Facility: The physical installation where fluids coming from the wellhead are separated into three main constituents: water, oil, and natural gas.

Usually it is most economical to use three to four stages of separation for the hydrocarbon mixture. Five or six may payout under favorable conditions, when — for example — the incoming wellhead fluid is found at very high pressure. However, the increase in liquid yield with the addition of new stages is not linear. For instance, the increase in liquids gained by adding one stage to a single-stage system is likely to be substantial. However, adding one stage to a three or four-stage system is not as likely to produce any major significant gain. In general, it has been found that a three-stage separating system is the most cost-effective. Figure 20.2 shows this typical configuration.
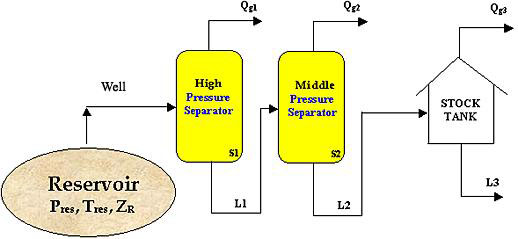
Under the assumption of equilibrium conditions, and knowing the composition of the fluid stream coming into the separator and the working pressure and temperature conditions, we could apply our current knowledge of VLE equilibrium (flash calculations) and calculate the vapor and liquid fractions at each stage. However, if we are looking at designing and optimizing the separation facility, we would like to know the optimal conditions of pressure and temperature under which we would get the most economical profit from the operation. In this context, we have to keep in mind that stage separation aims at reducing the pressure of the produced fluid in sequential steps so that better and more stock-tank oil/condensate recovery will result.
Separator calculations are basically performed to determine:
- Optimum separation conditions: separator pressure and temperature
- Compositions of the separated gas and oil phases
- Oil formation volume factor
- Producing Gas-Oil ratio
- API gravity of the stock tank oil
Let us look at the case of three-stage separation. In general, temperature conditions in the surface separation facility are very much determined by the atmospheric condition and incoming stream temperatures. As for pressures, the very first separator pressure is controlled by the gathering lines coming from well heads, thus there is not much room for playing with pressure in the first separator. The same arguments are valid for the last stage of separation (stock tank), which usually operates at atmospheric conditions. Therefore, we are only left with the middle separator for optimization.
As it turns out, the key to designing a three stage separation system is finding the optimum pressure at which to operate the second separator. The question that we would answer is “what is the pressure that will result in the best quality liquid going out of the stock tank for sales?” We do not want to do this empirically. This is, we do not want to play with the second stage separator pressure in the field, until we ultimately find the optimum condition. What we can do, using our phase behavior knowledge, is to find this optimum middle stage pressure applying our understanding of VLE equilibrium.
Figure 20.3 shows the typical effect of playing with the middle separator pressure on the quality and quantity of produced oil/condensate at the stock tank. Quality and quantity are measured in terms of properties, such as API and Bo, and the overall GOR at the separation facility.
The optimum value of pressure for the middle stage is the one that produces the maximum liquid yield (by minimizing GOR and Bo) of a maximum quality (by maximizing stock-tank API gravity). The smaller the value of GOR and Bo, the larger the liquid yield. The higher the API gravity of the stock-tank fluid, the more profitable its commercialization. From Figure 20.2, we see that this condition is found at neither extreme (low/high) values of middle stage pressure. There is, in fact, an optimal value for middle stage pressure. This is the value we are looking for.
The Phase Behavior model that we have described throughout these series of lectures provides the basic framework for the type of calculations required here. Additionally, we discussed how API and Bo can be calculated using the output of the phase behavior model. While doing the calculations for a 3-stage separating system, keep in mind that we have minimal control over feed pressure, as we do not want to inhibit the well (high-pressure separator). We do not control the sales line pressure (stock-tank pressure) either. The control that we do have is the operating pressure of the middle separator.
Recall that finding the optimum pressure calls for, in part, finding the minimum gas to oil ratio (GOR, SCF/STB). We are dealing, in this case, with total GOR. The total GOR is the cumulative amount of gas from all three separators divided by the amount of liquid/condensate leaving the stock tank. During our discussion on Bo-calculations, we called “nst” the moles of liquid leaving the stock tank per mole of feed entering the separation facility. This number can be obtained by sequentially flashing 1 lbmol of feed through each of the separation stages. Recalling the definition of GOR,
where:
[basis: 1 lbmol of feed]
Therefore,
Usually, the stock tank is considered to operate at standard conditions (psc, Tsc). Now you are ready to make your own surface separation design!
Compositional Modeling of Gas-Condensate Reservoirs:The Zero-dimensional Approach
Phase behavior is relevant to every aspect of petroleum and natural gas engineering. According to the complexity of the reservoir fluid phase behavior, reservoir modeling is classified under two distinct groups: black-oil simulation and compositional simulation. ; Often times, it is safe to assume that reservoir fluid behavior is only a function of pressure and independent of composition. This simplified behavior is typical of “black-oil” systems. In this case, reservoir hydrocarbon fluids are assumed to be comprised of two components, namely oil and gas. The model allows for certain amount of gas to be in solution with the oil at reservoir conditions. The amount of dissolved gas increases with, and is a sole function of, pressure for conditions below the bubble point. Above the bubble point pressure, the oil-component carries all the available gas in the reservoir, and a “variable bubble point” algorithm is usually implemented to predict conditions for the release of the dissolved gas. For this “black-oil” simplified model to be valid, actual oil and gas phases should maintain a fixed-composition throughout the process simulated in the reservoir. In certain cases, the assumption of fixed oil and gas composition is no longer valid: for instance, depletion of gas-condensate reservoirs and volatile-oil reservoirs, and processes that aim at the vaporization or miscible flooding of the in-situ fluids by fluid injection. More complex fluid behavior requires treating all hydrocarbon phases as nc-component mixtures and thus performing a “compositional simulation.”
Although the need for taking compositional dependence of thermodynamic and hydrodynamic parameters into account in reservoir description has been recognized for a long time, the actual implementation has not been realized until relatively recently. One of the main reasons is due to the lack of simple and reliable methods of predicting phase behavior under the conditions of interest. Two things have happened within the last three decades that have changed the situation: They are (1) the availability of fast and relatively inexpensive computational power to carry out the great number of calculations involved and (2) the development of samples and fairly good equations of state.
Simply put, a compositional reservoir simulator is a dynamic integration of the fluid dynamic porous media model and the phase behavior model, neither of which is subordinated to the other. In fact, in the early days of compositional reservoir simulation, a non-dynamic integration of these two was the norm. The more recent models actually attempt a full dynamic integration. The need for integration had been recognized earlier particularly for gas condensate reservoir, gas cycling processes, and volatile oil systems.
Early developments in reservoir engineering analysis relied on zero-dimensional or tank material balances for the evaluation and forecasting of reservoir performance. In 1936, Schilthuis devised what we now regard as the classical material balance equation. Schilthuis-type material balances are only valid for black-oil systems and are not applicable for reservoir fluids with complex behavior such as gas condensates and volatile oils. Compositional considerations were incorporated into zero-dimensional modeling in the decade of 1950’s with the works of Allen and Row (1950), Brinkman and Weinaug (1957), Reudelhuber and Hinds (1957), Jacoby and Berry (1957), and Jacoby et al. (1959). These can be regarded as the first generation of compositional simulators. Even though zero-dimensional simulations have been largely overthrown by more sophisticated numerical simulation techniques, they are still considered the most simple and fundamental tool available for the analysis of reservoir performance.
The zero-dimensional models make two principal assumptions. The first is to basically ignore the two-way coupling between fluid’s thermophysical properties and the hydrodynamic characteristics. The reservoir is treated as a perfectly mixed tank reactor with uniform properties. We assume no dimensions, and that one single value of pressure and temperature describes the average behavior of the entire reservoir. The second assumption is to neglect the hydrodynamic interactions between the flowing gas and liquid phases. In other words, the zero-dimensional compositional model relies on phase behavior as the most crucial effect controlling the description of recovery performance.
There is no doubt that significant insights, albeit qualitative, are provided by these studies. Zero-dimensional modeling provides a less expensive tool for the engineer to gain some insight into the expected performance of a gas condensate reservoir under depletion. Sometimes we spend a great deal of time dealing with the numerics of the dimensional compositional simulators, and we may forget that phase behavior is the single most important constituent of the depletion performance of, for instance, gas-condensate systems. Nevertheless, the reservoir engineer must keep in mind that this type of analysis does not provide the most accurate reservoir description. For instance, the effect of heterogeneities on reservoir performance cannot be studied with a zero-dimensional model. Again, the goal is to take a look at the qualitative insights that fluid PVT behavior can provide us.
The typical depletion sequence that a zero-dimensional compositional simulator follows is described below. This classical analysis treats gas condensate performance as constant volume depletion (CVD) in a PVT cell. The ultimate output of the model is basically comprised of GOR prediction and the compositions of the gas and condensate surface effluents. We start with a single-phase gas reservoir fluid, of a known composition, at an initial reservoir pressure and temperature. We flash this fluid several times through a series of pressure depletion stages until abandonment conditions are found. Reservoir volume is kept constant throughout the depletion process.
The typical depletion sequence that a zero-dimensional compositional simulator follows are listed below:
- Calculate the density and molecular weight of the initial reservoir fluid. With this information, and knowing the initial reservoir volume (Vti), calculate the initial amount of gas in place (lbmols). An alternative approach is to start with a fixed amount of lbmols of reservoir fluid, and calculate the corresponding initial reservoir volume (Vti). We assume a volumetric reservoir and thus the initial reservoir volume (Vti) is kept constant throughout the calculations.
- Using the reservoir fluid composition, distribute the initial moles of reservoir fluids into components, and store such quantities for material balance accounting.
- Depletion step: Lower the reservoir pressure by a given amount (typically, 200 psi). Flash the reservoir fluid at the new pressure, calculate amount of moles in the gas and liquid phases (“GasT” and “LiqT”) and the densities and molecular weights of each of the phases at the new condition.
- Expansion: With molecular weight, density, and total molar amount of each of the phases, calculate the new total volume that the fluids occupy at the new condition (Vexp).
-
Calculate the excess volume of fluids, taking the difference between the new volume upon expansion (Vexp) and the reservoir volume (Vti). This represents the volume of fluid that must have been withdrawn by the well in order to reach the newly imposed pressure condition, i.e.
Vws = Vexp – Vti(20.3) - Calculate the percentage of liquid in the well stream using mobility ratio considerations. Trial and error procedure is necessary for the liquid accounting. The total amount of liquid available upon depletion (LiqT) must be distributed between the wellstream (LiqWS) and the liquid remaining in the reservoir (LiqR). Additionally, the moles of reservoir liquid “LiqR” can be expressed in terms of oil/condensate saturation. Oil saturations define the mobility of the gas and liquid phases. These interrelations are shown below:
(20.4a)(20.4b)(20.4c)(20.4d)
LiqWS is a function of mobility ratio, which is a function of LiqR (through So). As a first guess, take LiqR = LiqT and calculate the corresponding LiqWS. Make new guesses (decreasing the value in every new trial) until the liquid balance in Equation (20.4a) is satisfied.
- Once LiqWS and (Vws)liq are known, obtain the total volume of gas withdrawn from the reservoir by subtracting the liquid volume (Vws)liq from the total wellstream volume (Vws). Express this gas volume in moles using reservoir gas density and molecular weight. Calculate the total number of moles of the wellstream.
- Material Balance Accounting: Calculate the number of moles of each component remaining in the reservoir. To do this: subtract the number of moles leaving the well stream from the number in the reservoir before flashing for each of the components. Calculate the new overall composition of the reservoir fluid.
- Calculate the overall composition of the produced well stream, by mixing the composition of gas and liquid coming along.
- Surface Production Facility: Flash the incoming wellstream composition through the train of separations. Calculate the total amount of gas and liquid leaving the separation facility and GOR. Calculate the percentage of recovery from the reservoir.
- A depletion loop has been completed. Go back to step 3 until abandonment pressure is reached (typically, 600 psia).
- Plot liquid production, gas production, GOR, and recovery from the reservoir as a function of pressure depletion, from initial reservoir conditions to abandonment conditions.
The basic VLE calculations required here can be performed using the Peng-Robinson EOS and equilibrium considerations. Liquid viscosities can be calculated through the Lohrenz, Bray, and Clark correlation, and gas viscosities can be calculated using the Lee-Gonzalez correlation. Fluid densities are obtained directly through the Peng-Robinson EOS.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
- API, GOR and Bo are the parameters that we use to optimize a train of separators. Speculate on why all three parameters seem to predict the same optimal separator pressure.
- Although zero-dimensional modeling can be used to model behavior of gas-condensate systems, there are some pitfalls in the description. What are these pitfalls? In what cases can we overlook them?
Engineering Applications (II)
Module Overview
Module Goal: To highlight some of the important applications of phase behavior in production operations.
Module Objective: To highlight the use of phase behavior for the description of gas pipelines, gas metering and hydrate systems.
Natural Gas Pipeline Modeling
Once natural gas is produced and processed, few to several hundred miles may lie in between it and its final consumers. A cost-effective means of transport is essential to bridge the gap between the producer and consumer. In the technological arena, one of the challenges pertains to the capacity of the industry to ensure continuous delivery of natural gas while its demand is steadily increasing. Thus, it is no wonder that pipelines have become the most popular means of transporting natural gas from the wellhead to processing — and from there to the final consumer — since it better guarantees continuous delivery and assures lower maintenance costs.
Phase Behavior (P-V-T data) is crucial for all our engineering designs. Accurate prediction of the P-V-T properties of natural gases is especially critical when dealing with pipeline design, gas storage, and gas measurement. While describing natural gas pipeline design, it is necessary to distinguish between two cases: the design of pipelines for transportation of regular dry gases (no liquid, single-phase transportation) and the design of pipelines for transportation of wetter gases — where multiphase conditions due to condensate dropout may are possible.
The major variables that affect the design of gas pipelines are: the projected volumes that will be transported, the required delivery pressure (subject to the requirements of the facilities at the consumer end), the estimated losses due to friction, and the elevation changes imposed by the terrain topography. Overcoming such losses will likely require higher pressure than the one available when the gas is being produced. Thus, forcing a given gas rate to pass through a pipeline will inevitably require the use of compressor stations.
Loss in mechanical energy results from moving fluids through pipelines. Energy losses in a pipeline can be tracked by virtue of the pressure and temperature changes experienced by the flowing stream. Design equations relate pipeline pressure drop with the gas flow rate being transported. The following is the general equation for a single-phase gas pipeline flow in steady state:
Note that flow rate is proportional to the inverse square root of compressibility (Z). For near-ideal conditions, the effect of compressibility on flow rate is likely to be small. But for high-pressure flows, Z may deviate greatly from 1. Under these conditions, inaccuracy in the prediction of Z may lead to a substantial error in the calculated flow rate and thus a completely wrong pipeline sizing for design purposes.
Once a pipeline is deployed, it has a more or less a fixed operational region. An upper and lower set of operational conditions allowable within the pipeline (in terms of pressure and temperature) will exist. On the one hand, the upper allowable condition will be set by the pipe strength, pipe material, diameter, and thickness. These will dictate the maximum pressure that the pipe can endure without failure (i.e., maximum operating pressure). On the other hand, maximum pressure and temperature of the compressor station discharge (which feeds the inlet of the pipe) will also contribute to set this upper level. It is clear that the conditions at the discharge of the compressor station cannot go beyond the maximum operating pressure of the pipe — otherwise the pipe will fail. The minimum or lower pressure and temperature condition of the operational region will be assigned by contractual agreement with the end consumer. The foregoing description of the operational region is shown schematically as the shaded area in Figure 21.1.
In natural gas flow, pressure and temperature changes (P-T trace) may cause formation of a liquid phase owing to partial condensation of the gaseous medium. Retrograde phenomenon — typically found in multi-component hydrocarbon systems — takes place by allowing condensation of the gas phase and liquid appearance even under expansion of the flowing stream. The same phenomenon may also cause vaporization of the liquid phase such that it reenters the gas phase. Liquid and gas phase composition are continuously changing throughout the pipe due to the unceasing mass transfer between the phases. In general, the amount of heavies in the stream determines the extent of the retrograde behavior and liquid appearance. Figure 21.1 shows a P-T trace or operational curve for a given pipeline, which is always found within the pipeline operational region.
Figure 21.1 also shows four typical phase envelopes for natural gases, which differ in the extent of their heavy components. For a given composition, the prevailing pressure and temperature conditions will determine if the fluid state is all liquid (single-phase), all gas (single-phase) or gas-liquid (two-phase). Each envelope represents a thermodynamic boundary separating the two-phase conditions (inside the envelope) from the single-phase region (outside). Each envelope is made of two curves: the dew point curve (right arm, where the transition from two-phase to single-gas occurs) and the bubble point curve (left arm, where the transition from single-liquid to two-phase occurs). Both arms meet at the critical point, which is shown in Figure 21.1. The wetness of the gas is an important concept that helps to explain the different features presented in Figure 21.1. This concept pertains to the amount of heavy hydrocarbons (high molecular weight) that are present in the gas composition. In Figure 21.1, the driest gas — i.e., the least wet — can be recognized as that whose left and right arms are the closest to each other, having the smallest two-phase region (gas A). In this figure, it can be seen that the right arm is extremely susceptible to the presence of heavies in the natural gas composition. Depending on the gas composition, the pipeline operational region can be either completely free of liquid (gas A, the driest) or partially submerged in the two-phase region (gas B, C). If the gas is wet enough, the pipeline will be entirely subjected to two-phase conditions (gas D, the wettest). One may describe the sensitivity of the right arm to heavies as having a hook-seizing effect: the larger the extent of heavies in the natural gas, the more the ‘hook’ is able to seize part of the pipeline operational region. In conclusion, since the operational region is more or less given by contractual and design considerations, the liquid presence in a pipeline is ultimately dictated by the properties of the gas that is being transported.
In the preceding figure, a pipeline handling a dry gas (gas A) will be operating a single-phase mode from its inlet through its outlet. For this case, any of the popular single-phase gas equations (Weymouth, Panhandle type, AGA equation) can be used for design purposes and to help to predict the actual operational curve (P-T trace). If a richer gas comes into the system (gas C), it will show a single-phase condition at the inlet, but after a certain distance the pressure and temperature conditions will be within the two-phase region. The case might also be that the system is transporting a wetter gas (gas D), in which case it would encounter two-phase conditions both at the inlet and at the outlet of the pipe.
Penn State has devoted a great deal of effort in the development of two-fluid models for the description of multi-phase flow condition in natural gas pipelines. In this approach, mass, momentum, and energy equations are solved simultaneously. Some simplifying assumptions are made based on engineering judgment. For instance, the knowledge of averaged flow field characteristics and fluid properties at every point of the pipeline is usually more meaningful than a detailed profile of the said properties within the cross section. Hence, generally speaking, the two-fluid model always deals with conservation equations written only in one dimension for pipeline flow (the direction of the flow along the pipe), employing cross-sectional-averaged values for each term. The use of averaged quantities absorbs the variations across the pipe section. Pressures and temperatures are assumed to be the same in both phases at any given point of the pipe. Additionally, since the main interest is to focus on normal operation conditions, the further simplification of steady state conditions is invoked.
As we have discussed, phase behavior is a crucial component in pipeline design. Not only because we need to account for gas volumetric behavior in the design equations (through, for instance, Z-factor calculations), but also because it provides a means for predicting whether multi-phase flow conditions are to be found. Liquid appearance in natural gas pipelines is as undesirable as it is inevitable. On one side, the fluid phase behavior and prevailing conditions make it inevitable. On the other, the condensate subjects the gas pipe to an increasing and undesirable energy loss. Thus, a proper pipeline design must account for the effect of condensate formation on the performance of the gas line.
The Hydrate Problem
Natural gas hydrates are solid crystalline compounds of snow appearance with densities smaller than that of ice. Natural gas hydrates are formed when natural gas components, for instance methane, ethane, propane, isobutene, hydrogen sulfide, carbon dioxide, and nitrogen, occupy empty lattice positions in the water structure. In this case, it seems like water solidifying at temperatures considerably higher than the freezing point of water.
Gas hydrates constitute a solid solution—gas being the solute and water the solvent—where the two main constituents are not chemically bounded. Figure 21.2 presents a typical phase diagram for a mixture of water with a light, pure hydrocarbon (HC), similar to that presented by McCain (1990).
Phase Diagram for a Water/Hydrocarbon (HC) System.
Shows ICE+HC Gas: Low temperature, low pressure
Hydrate+Ice: Low temperature, Higher Pressure
Hydrate+Free Water: Mid temperature range, medium/high pressure
Water+Hydrocarbon Gas: Mid to high temperature, lower pressure than Hydrate + Free water and Liquid HC + Water, but increasing with temperature
Line between Hydrate + Free Water and Water + Hydrocarbon gas is labeled as conditions at which gas and liquid water combine to form hydrates
Liquid HC +Water: Higher temperature, Higher pressure
There are a number of points on the diagram in Figure 21.2 that are noteworthy. First of all, hydrate formation is clearly favored by low temperature and high pressure. The three-phase critical point is point C on the diagram that represents the condition where the liquid and gas hydrocarbon merge into a single hydrocarbon phase in equilibrium with liquid water. Point Q2 is the upper quadruple point, where four phases (liquid water, liquid hydrocarbon, gaseous hydrocarbon, and solid hydrate) are found in equilibrium. Point Q1, the lower quadruple point, typically occurs at 32 °F (ice freezing point) where four phases (ice, hydrate, liquid water, and hydrocarbon gas) are found in equilibrium. In this context, phases are not pure as they contain some amount of the other substances according to their mutual solubility.
For practical applications, the most important equilibrium line is the Q1Q2 segment. It represents the conditions for hydrate formation or dissociation, a critical piece of information for most industrial applications where hydrates are involved. When we focus on this zone, the phase behavior of water/hydrocarbon system is simplified to the schematics shown in Figure 21.3.
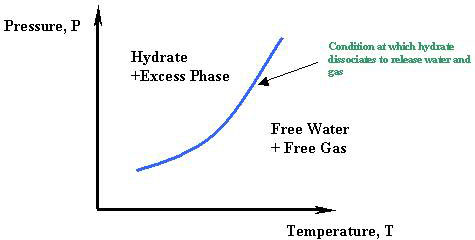
Phase Behavior thermodynamics is usually invoked for the prediction of the Q1Q2 hydrate formation/dissociation line. The first two methods of prediction were proposed by Katz and coworkers, and are known as the Gas Gravity Method (Katz, 1945) and the Ki-value Method (Carson and Katz, 1942). Both methods allow calculating the P-T equilibrium curves for three phases: liquid water, hydrate and natural gas. These methods yield initial estimates for the calculation and provide qualitative understanding of the equilibrium; the latter method being the more accurate of the two. The third method relies on Statistical Mechanics for the prediction of equilibrium. It is recognized as the most accurate of all three-phase calculations as it is more comprehensive and detailed.
The key circumstances that are essential for hydrate formation can be summarized as:
- Presence of “free” water. No hydrate formation is possible if “free” water is not present. Here, we understand the importance of removal of water vapor from natural gas, so that in case of free water occurrence there is likelihood of hydrate formation.
- Low temperatures, at or below the hydrate formation temperature for a given pressure and gas composition.
- High operating pressures.
- High velocities, or agitation, or pressure pulsations, in other words turbulence can serve as catalyst.
- Presence of H2S and CO2 promotes hydrate formation because both these acid gases are more soluble in water than the hydrocarbons.
The best and permanent remedy for the hydrate formation problems is the dehydration of the gas. Sometimes, it is quite possible that hydrates will form at the well site or in the pipeline carrying natural gas to the dehydration unit, so that the need for well head techniques arises. At well site, two techniques are appropriate:
- Heating the gas stream and maintaining flow lines and equipment at temperature above the hydrate point,
- In cases where liquid water is present and the flowlines and equipment cannot be maintained above hydrate temperature, inhibiting hydrate formation by injecting additives that depress both hydrate and freezing temperatures.
The most common additives are methanol, ethylene glycol, and diethylene glycol. Methanol injection is very beneficial in cases where a low gas volume does not permit the dehydration processing. It is also extremely useful in cases where hydrate problems are relatively mild, infrequent, or periodic, in cases where inhibitor injection is only a temporary phase in the field development program, or where inhibition is done in conjunction with a primary dehydration system.
Gas Metering
Gas measurement is another area of hydrocarbon engineering where accurate prediction of the P-V-T properties of the working fluid is especially critical. One of the most widely used meters used in the measurement of gas flow is the orifice meter. Orifice meters are classified as inferential meters because the gas volume is calculated from readings of pressure variation as the gas passes through an orifice, and it is not obtained by a direct reading.
The orifice meter is arranged so that the flowing gas is constricted at a particular location by a thin orifice plate very accurately gauged and calibrated so as to be in a concentric position in the pipe. The reduction of the cross section of the flowing gas stream in passing through the orifice increases the velocity head at the expense of the pressure head, and the reduction in pressure between the taps is measured by manometers (or a recording meter). A typical orifice meter is shown in Figure 21.4.
Among the advantages of using orifice meters for gas measurement purposes are the following facts:
- They are simple in design and have no moving parts.
- They are relatively accurate.
- They are easy to install and maintain.
- They cover a wide range of capacity.
- They represent a low cost.
- There is a great deal of experience in their use.
Among the disadvantages of orifice meters are the following facts:
- They represent an intrusive measurement technique and a flow restriction that translates into a large energy loss.
- The orifice hole can be eroded by sand or corrosive fluids.
- The hole may be obstructed by wax or hydrate.
Among the advantages of using orifice meters for gas measurement purposes are the fact that they are simple in design and have no moving parts, relatively accurate, easy to install and maintain, cover a wide range of capacity, represent a low cost, and there is a great deal of experience in their use. Among the disadvantages of orifice meters, are the fact that they represent an intrusive measurement technique and a flow restriction that translates into a large energy loss, the orifice hole can be eroded by sand or corrosive fluids, and the hole may be obstructed by wax or hydrate.
Bernoulli’s equation is then used as the basis for correlating the increase in velocity head with the decrease in pressure head. In the calculation of gas flow rate using an orifice meter, two quantities must be measured: the static pressure (i.e. the line pressure) and the differential pressure (i.e. the pressure drop across the orifice plate). The following is the basic equation for gas flow through an orifice meter:
In Equation (21.2), flow rate is a function of gas compressibility factor (Z). Again, for high-pressure flows, an error in the compressibility factor could result in an erroneously calculated flow rate. If you have some error on Z-factor, this automatically translates into error in the gas meter. Accurate phase behavior prediction techniques are a must in gas metering.
In the Natural Gas Industry, the point of gas exchange between the buyer and the seller is called custody transfer. During custody transfer operations, accurate measurements of the quantity and quality of the exchanged gas are of crucial importance because of its economical implications. Economic transactions are based on volumetric rate measurements, which are regulated to be made at the same base conditions. Industry base conditions or standard conditions (SC) are usually taken as P = 14.7 psia and T = 60.0 °F. A low percent inaccuracy in the Z-factor calculation of a gas in transfer can easily translate into thousands of dollars of losses on a daily basis! In fact, flow rate estimations can prove extremely sensitive to values of compressibility factor. This is why the gas industry does not accept Z-factor predictions with a range of uncertainty larger than + 0.01 % for custody transfer operations.
Action Item
Answer the following problem, and submit your answer to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
- Write an essay that describes the applicability of the knowledge gained in this course to several other areas in the petroleum and natural gas business. Provide specific examples.