Phase Diagrams, Part II
Module Goals
Module Goal: To familiarize you with the basic concepts of phase diagrams as a means of representing thermodynamic data.
Module Objective: To familiarize you with the use of P-T and P-v diagrams.
Vapor Pressure Curve
From the last module you will recall that the vapor-pressure curve (Figure 2.3) and its extremities were examined. That figure is presented in this module in Figure 3.1. We concluded that two very important thermodynamic points bound the vapor pressure curve: the Critical Point at its upper end and the Triple Point at its lower end.
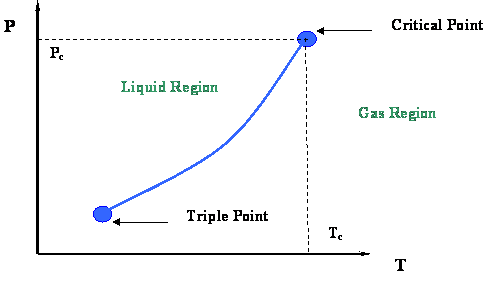
Now let us take a second look at this figure. We can better understand the information represented by the vapor pressure curve by looking at the process of isobaric heating. This is illustrated by line ACB in Figure 3.2. The term “isobaric” pertains to a constant pressure process. By isobaric heating process, we then mean a “constant pressure addition of heat into a system.”
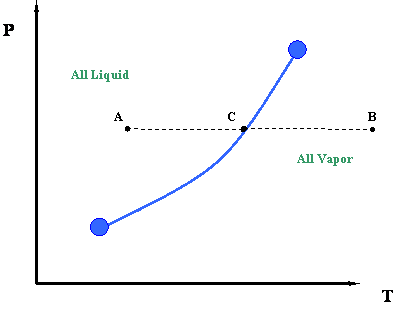
Such a process can be described as follows. Starting at point A and moving towards point C at constant pressure, we add heat to the system. By adding this heat, we cause a temperature increase in the system (Temperature at C > Temperature at A.). At point C, which lies above the vapor pressure or boiling point curve, we encounter a phase change. To the left of point C, at lower temperatures, exists only liquid. To the right of point C, at higher temperatures, there is only vapor. Therefore, a sharp discontinuity in density exists at point C. During this transition, from liquid to vapor, we will notice that the heat that we add to the system does not cause any temperature increase, and in fact, temperature and pressure conditions remain constant during the transition represented by the vapor curve. In other words, even though we are adding heat, the system remains at the pressure and temperature associated with point C until the whole phase transition has taken place — i.e., until all the vapor is converted to liquid. Instead of working to increase liquid temperature, this heat serves to move liquid molecules apart until all liquid has become vapor.
Up to this point, we saw that the heat added before the system reached the phase transition was used to raise the temperature of the substance. However, the heat that we are adding right now, during the phase transition, is not causing any temperature increase (hence it is said to be hidden heat or latent heat of vaporization). Therefore, we differentiate between two kinds of heat: sensible heat and latent heat.
Sensible Heat: Its main purpose is to cause an increase in temperature of the system.
Latent Heat: It serves only one purpose: to convert the liquid into vapor. It does not cause a temperature increase.
In fact, the name “latent” suggests “hidden.” Here, we are adding heat to the system but are not seeing its effect in terms of temperature increase. The heat that is needed to transform one mole of saturated liquid into vapor is known as the latent molar heat of vaporization: 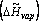
Once we have converted all the liquid into vapor (i.e., we supplied all the necessary latent heat to accomplish this), we may continue to add more heat. If we do so, the temperature will rise again and we will end at point B (Figure 3.2). This heat is also sensible since it is causing the temperature of the system to rise.
It is interesting to note that, in order to reverse the process from point B to point A, we will have to remove the exact amount of heat that we had added before. This is a basic consequence of an energy balance principle. We call such a reverse process an isobaric cooling process. We will have to remove some sensible heat in order to cool the vapor from point B to C, and then we will remove all the latent heat of the vapor to condense it into liquid (transition at point C). Finally, we will also need to remove more sensible heat from the system for the cooling of the liquid from point C to point A.
In the previous two processes, from A to B or vice versa, we had to cross the phase boundary represented by the vapor pressure curve. However, this is not the only thermodynamic path that is available for us to go from A to B. Figure 3.3 depicts another possible path.
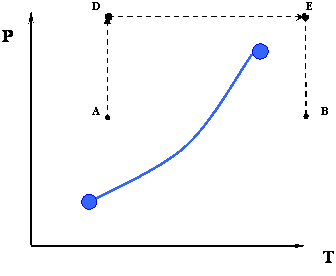
Instead of doing the whole process isobarically, we may devise a new path that may also accomplish the goal of taking the system from a condition ‘A’ to a condition ‘B.’ Consider the path ADEB that is shown in Figure 3.3.
Sequence of Paths
- Path AD: Isothermal compression
- Path DE: Isobaric heating
- Path EB: Isothermal expansion
There is something remarkable about this new path. Unlike the previous path, notice that we do not cross the phase boundary at all. The consequences of taking this new road may seem astonishing at first glance: we went from an all-liquid condition (point A) to an all-vapor condition (point B) without any sharp phase transition. In fact, along the path ADEB there is NO phase transition because we never crossed the phase boundary. Since the phase boundary represents a sharp discontinuity in density (and other physical properties), the fact that we are not crossing it tells us that as we go, there is actually a gradation in density (from a liquid like, or high-density at point A to a gas like, or low-density at point B) instead of a sharp change from the high liquid density to the low gas density.
We were able to do so because we went above the critical conditions. In the vicinity of and beyond critical conditions, we are no longer able to distinctly label the single-phase condition as either “liquid” or “gas”. Under these conditions, any transition takes place gradually without any differentiation between a ‘liquid’ and a ‘gas’ phase. We call this fluid, which we cannot define either as a liquid or as a gas, a supercritical fluid. In terms of density, a supercritical fluid may be described, at the same time, as a light liquid (its density is not as high as the liquid density) and a heavy gas (its density is not as low as the typical gas density of the given substance). The behavior of fluid around this area is an active and interesting area of current research.
In summary, for a pure substance, you can avoid having an abrupt phase transition (such as the one described by the path ACB) by going around the critical point (path ADEB). Keep in mind that any path that crosses the vapor pressure curve (ACB) will undergo a phase transition.
PV Diagram for Pure Systems
In the previous discussion, we used the P-T diagram and were not concerned about changes in the volume of the system. If we want to follow changes in volume, we may construct P-v or T-v diagrams, in which we hold temperature (T) or pressure (P) constant. Let us consider the case of a P-v Diagram (Figure 3.4).
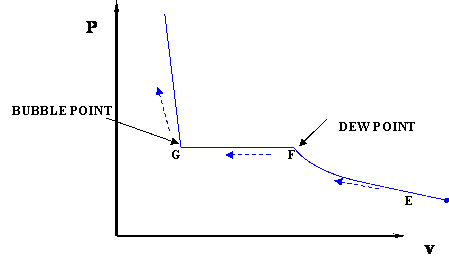
In this case temperature is being held constant; our substance is undergoing an isothermal compression process. Starting at E (all-vapor condition), an increase in pressure will result in a rather significant reduction in volume since the gas phase is compressible. If we keep compressing isothermally, we will end up at point F, where the gas will be saturated and the first droplet of liquid will appear. We have come to the two-phase condition, where liquid (L) and vapor (V) co-exist in equilibrium, for the first time, albeit an infinitesimal amount of liquid.
Once we reach the two-phase condition, what happens is not intuitive. While we keep on compressing by decreasing the volume (path F-G,) the pressure of the system remains constant; this condition continues until all the vapor has become liquid. Point G represents the last condition of liquid and vapor (L+V) coexistence, saturated liquid condition (liquid in equilibrium with an infinitesimal amount of vapor.) Once we have only liquid, if we keep on compressing (i.e., attempting to reduce liquid volume) we will observe a rapid increase in pressure, as indicated by the steep slope in the P-v diagram. This is because liquid is virtually incompressible, hence, a great deal of pressure is needed to cause a small reduction in volume.
It is important to recognize some points of this process. If we recall our previous definitions of basic concepts, we will recognize point F, where only a tiny quantity of liquid exists in an otherwise completely gaseous system (the dew point of the system at the given temperature). Similarly, Point G is the bubble point; only an infinitesimally small bubble of vapor exists in an otherwise liquid system.
But wait a second. Let us try to compare Figure 3.4 with Figure 3.2. Can we relate them to each other? Where is path F-G in Figure 3.4 represented in Figure 3.2 (repeated below)?
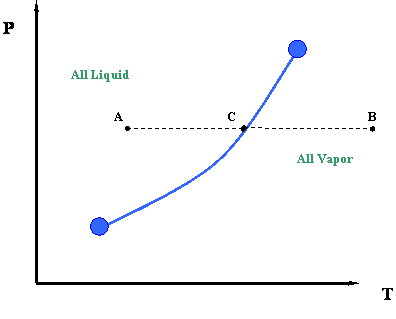
The answer is, path F-G is represented by one point in Figure 3.2; that is, point C. Recall, for a single-component system, dew points and bubble points are identical. During a phase transition, both pressure and temperature must remain constant for pure components.
Now, if we want to generate all the possible points that make up the vapor pressure curve in Figure 3.2, we would need to repeat the experiment for different temperatures. We would end up with a family of isotherms (each similar to the one presented in Figure 3.4). This is represented in Figure 3.5.
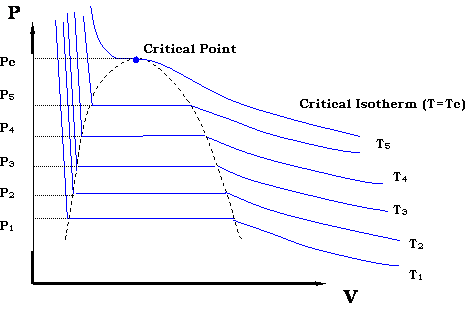
The zone where the isotherms become flat delineates the two-phase region. It is clearly seen that by plotting all the pairs in that zone (P1,T1), (P2,T2)… (Pc, Tc) we will be able to reproduce Figure 3.2.
If we now draw a line through all the Bubble Points in Figure 3.5, and then draw a line connecting all the Dew Points, we will end up with the Bubble Point Curve and the Dew Point Curve, respectively. It is clear that the two curves meet at the critical point (Pc, Tc). Furthermore, the two curves delineate the phase envelope, which contains the 2-phase region inside. If we “clean” Figure 3.5 a little, we end up with the phase envelope that is shown in Fig. 3.6.
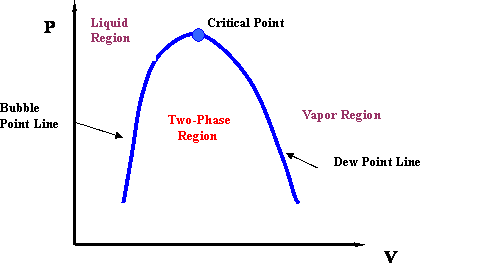
If you carefully follow the trend of the critical isotherm (@ T = Tc in Fig. 3.5), you will realize that it has a point of inflexion (change of curvature) at the critical point. Furthermore, the critical point also represents the maximum point (apex) of the P-v envelope. Mathematically, this information is conveyed by the expressions:
$$\left(\frac{\partial P}{\partial \vec{V}}\right)_{P C, T C}=\left(\frac{\partial^{2} P}{\partial \vec{V}^{2}}\right)_{P C T C}=0$$
which are usually known as the criticality conditions. These conditions are always satisfied at the critical point. We will comment more on this after we begin the discussion on Equations of State (EOS) — semi-empirical relationships that mathematically model the P-v-T behavior of fluids.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
- Explain in your own words (no more than a paragraph) why the 2-Phase segment of the P-v isotherm should correspond to one single point in the P-T diagram.
- What about the critical point in the P-T diagram? Which P-v isotherm could that correspond to?
- Take two different hydrocarbons (say, C1 and C2) and compare their P-T vapor pressure curves. What do you notice? As you saw in the previous module, those P-T curves will be found at different conditions of pressure and temperature. But more than that, what can you comment about the slopes of both curves? Are they different? Why? Speculate.