Elementary Vapor-Liquid Equilibrium (I)
Module Goals
Module Goal: To establish the basic framework for vapor-liquid equilibrium calculations.
Module Objective: To establish the connection between real production processes and vapor liquid equilibrium calculation.
Introduction
In the next series of modules, we are going to look at how we can apply what we have learned so far to perform vapor/liquid equilibria calculations.
- First of all, we are going to review engineering systems and how the phenomenon of VLE is related to them,
- Then we will proceed by looking at how to describe the problem itself,
- We then will discuss the formulation the problem,
- And finally, we will discuss solution strategies.
These are the four main topics that we will look at in this module. As far as VLE is concerned, we can list a number of systems that are at the heart of petroleum fluid production that involve this phenomenon:
- Separators
- Reservoir
- Pipelines
- Wellbore
- LNG Processing
- NGL Processing
- Storage
- Oil and LNG Tankers.
Vapor/liquid equilibrium pertains to all aspects of petroleum production with which we are concerned. It is no wonder, then, that we devote a new module to the subject itself.
Consider the case of a typical transmission pipeline. As gas is injected at the inlet, the pressure will drop continuously along the length of the pipeline, due to friction. Even though we usually think of liquid as forming with increasing pressure — i.e., upon compression — we have to recall that the phenomena of retrograde condensation (discussed in Module 4) takes place in hydrocarbon mixtures. Therefore, contrary to expectations, most single-phase natural gasses yield liquid upon expansion. Therefore, as pressure drops in the pipeline, liquid may drop out as the thermodynamic path crosses the dew point line and enters the phase envelope. In this case, what started as a single phase flow became two-phase flow within the system.
We also encounter this phenomenon in gas condensate reservoirs. Your initial reservoir conditions may be outside the phase envelope, but as you deplete the reservoir, your production path may take the system inside the two-phase region. In these previous two examples, the single-most important property with which you are concerned is the dew point. You want to know dew point, since you would like to know at which point of the pipeline or at which stage of production liquid may start to form.
We also may have an oil reservoir, where the initial pressure and temperature conditions place us in the single-phase liquid region. As you produce, you deplete the reservoir and enter the two-phase region by crossing the bubble point curve. At this point, we would like to know the bubble point of the system so that we may anticipate the appearance of a gas phase within an originally-all-liquid reservoir.
In all these cases, by taking a sample of the fluid to the lab, we may be able to find the composition of the fluid. Hence, in these kinds of problems, composition is usually known, and so are temperature and pressure. Your unknowns are the dew point or bubble point condition.
Suppose we are not interested in what is happening in the reservoir, but rather in what is happening at the surface. You would then like to know how much liquid or gas you will have in your separators. In this case, you are no longer interested in bubble points or dew points, but rather the extent of the phases: how much liquid and how much gas the reservoir will be able to deliver at the surface. In this case, the composition of what is coming to your separator may be known, and the pressure and temperature of operation of each separation stage may be specified. We would want to know the quality and the quantity of what is coming out; that is, we need the compositions of the gas and oil that leave the separators and the flow rates of gas (MSCF/D) and oil (STB/D).
Types of VLE Problems
In a typical problem of liquid and vapor coexistence, we are usually required to know one or more of the following:
- The phase boundaries,
- The extent of each phase,
- The quality of each phase.
The main emphasis is on the quantitative prediction of the above. These three represent the three basic types of VLE problems. A more detailed description of each of them is given below.
- Phase Boundary Determination Problem
These types of problems are either a bubble-point or a dew-point calculation. They are mathematically stated as follows:
- Bubble-point T calculation: Given liquid composition (xi) and pressure (P), determine the equilibrium temperature (T),
- Bubble-point P calculation: Given liquid composition (xi) and temperature (T), determine the equilibrium pressure (P),
- Dew-point T calculation: Given vapor composition (yi) and pressure (P), determine the equilibrium temperature (T),
- Dew-point P calculation: Given vapor composition (yi) and temperature (T), determine the equilibrium pressure (P).
- Relative Phase Quantity Determination
In this type of problem, overall composition (zi), pressure (P), and temperature (T) are given, and the extent of the phases (molar fractions of gas and liquid) are required.
- Phase Quality Determination
In this type of problem, overall composition (zi), pressure (P), and temperature (T) are given, and the composition of the liquid and vapor phases is required.
Problems of types 2 and 3 are collectively referred to as flash calculation problems. All three are problems that we encounter in production operations as petroleum engineers. Our focus now is on solving these sorts of problems. We want to use a predictive approach to do so. This is, we want to use mathematical models — the most economical and convenient approach — to accomplish the task.
One of the assumptions that we are making here is that of equilibrium. We assume that at all times, vapor and liquid that are coexisting together are in equilibrium. Are they really in equilibrium? No! Nevertheless, the state of current knolwedge requires us to assume equilibrium so as to be able to proceed.
Formulation of the VLE Problem
We assume that the system is at steady state and at a state of equilibrium. Adopting these two assumptions is essential to the developing of the equations that we use to solve these problems. These assumptions are convenient for modeling and have proven useful in representing the real phenomena. In conclusion, we claim that the systems maintain a state that resembles equilibrium and does not depart from it greatly. And what does steady state means? Simply stated, we say that a system is at steady state when whatever comes into the system goes out. This is, no accumulation takes place within the system.
Let us consider the equilibrium cell shown in Figure 12.1. “F” moles of a feed enter our equilibrium cell with a composition “zi” and “nc” is the number of components that we have in the mixture. A flash vaporization takes place at a given pressure and temperature, and two streams come out: “V” moles of a vapor of composition “yi” and “L” moles of a liquid of composition “xi”. In steady state, a simple overall balance yields:
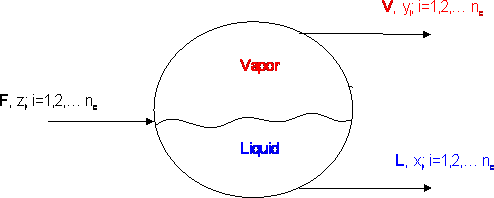
(12.1a)
Now we define the fractions of gas and liquid to be, respectively:
(12.1b)
(12.1c)
Therefore, if we divide equation (12.1a) by “F”, we get:
(12.2)
The same steady state assumption applies for the mass of each component separately. Here we revisit a concept we used in Module 5, when we studied the lever rule. At that point, we said that the number of moles of a component “i” per mole of mixture in the liquid phase is given by the product “xiaL”, while the number of moles of “i” per mole of mixture in the gas is given by “yiaG”. Since there are “zi” moles of component “i” per mole of mixture coming into the system, the conservation of each component in the system imposes:
(12.3)
Equation (12.3) is true for each of the components in the system. Equation (12.2) can be introduced into equation (12.3) to yield:
(12.4)
One of the concepts that we normally use in vapor-liquid equilibria is that of the equilibrium ratio, Ki. In fact, most of the computations of phase behavior of natural gas mixtures are carried out through the concept of the equilibrium ratio. By definition, the equilibrium ratio of a component “i” in a vapor-liquid mixture is defined as the ratio of the molar composition of that component in the vapor phase to that in the liquid phase,
(12.5)
In earlier literature, this concept was referred to as the equilibrium constant. In actuality, Ki is not constant but a function of the pressure, temperature, and composition of the system. However, equilibrium ratios can be fairly independent of composition when the pressure and temperature conditions are far from critical.
Therefore, today we refer to it as the vapor-liquid equilibrium ratio, Ki. We can introduce this concept into the balance in (12.4), as shown:
(12.6)
Now, solving for yi,
(12.7)
A constraint that mole fractions must satisfy is that they must add up to unity. Since we solved for yi, we can impose that the summation of all molar vapor fractions must be equal to one, i.e.,
(12.8)
If we now substitute (12.7) into (12.8), we get:
(12.9)
This equation is important for us; we call it an objective function because we can use it as the starting point for solving the vapor-liquid equilibrium problems we have posed.
However, as you may be thinking right now, this is not the only choice that we have for an objective function. In fact, we may obtain another objective function if we repeat the previous steps, while solving instead for xi. In this case, we may introduce the concept of equilibrium ratio in (12.5) into (12.6) as follows:
(12.10)
We now solve for xi,
(12.11)
If we apply the constraint that all mole fractions must add up to one,
(12.12)
Both (12.9) and (12.12) are plausible objective functions. Either of them allows us to solve the flash problem that we are dealing with. The variables that make up both equations are:
nc = Number of components,
zi = Overall composition, or composition of the feed,
Ki = Equilibrium ratios of each of the components of the mixture,
ag = Vapor fraction in the system.
What is it that we are looking for? Go back and look at the types of VLE problems that we would like to solve, as we presented them in the previous section. If we are interested in solving the flash problem, we want to know how much liquid and gas we will have inside the flash equilibrium cell. This is, given a liquid-vapor mixture of composition zi, and nc number of components, what percent of the total number of moles is liquid, and what percent is vapor? How do we split it? In this case, we would like to come up with a value for αl and αg respectively.
Equations (12.9) and (12.12) tell us that if we are able to come up with the proper values for the equilibrium ratios, Ki, which are functions of the pressure, temperature, and composition of the system, the only unknown left to solve for would be αg — exactly what we want!
Well, do not rush. We would have to come up with a way of calculating Ki’s first, and this may not be a trivial task. For the time being, let us say we “know” Ki’s. Two questions remain unanswered:
- First, is it “better” to solve the problem using equation (12.9) or (12.12)? (Recall, either of them would lead us to the answer!).
- Second, how do we solve for αg? For a complex mixture of many components, “αg” cannot be calculated explicitly.
We will address both of these questions in the next module. As for now, let us give you a hint: we will not use either equation (12.9) or (12.12) to solve the flash problem!
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
You are given two different phase envelopes (VLE region) that represent two different gas reservoir fluids. The first of them has a larger PT envelope covering larger P,T ranges. The other covers a fairly narrow P,T range. What do you conclude? Speculate on the type of gas reservoir for each case. Justify your answer.
-
In order to design the appropriate production scheme for a gas reservoir recently discovered, what type of VLE calculation do you think is more valuable? Explain in detail.