Implications of S-shaped curve (Sub-critical Conditions)
A major issue that has kept us banging our heads has been how to mathematically represent the discontinuity of the P-v isotherm during the vapor-liquid transition (Figure 6.3). Such a discontinuity shows up during the isothermal compression of any pure substance at sub-critical conditions (T < Tc). What we want here requires fitting a continuous mathematical function to a discontinuous, real-life event. Strictly speaking, it would be contradictory to find a single continuous mathematical function that can capture such a discontinuity in its full nature.
Can we really model the discontinuity? Not really, but we can get around it. van der Waals provided a possible solution in his dissertation on the “continuity of vapor and liquid.” Even though neither cubic equations nor any other continuous mathematical function is able to follow the discontinuity, what they can do is good enough for engineering purposes. The “cubic behavior” can reasonably match the liquid and vapor branches for the real, experimental isotherms.
Since van der Waals’ EOS, we have been able to consider the continuity between gas and liquid phases. Now, we need to learn how to deal with the S-shaped behavior, and to look at it as a minor, inconsequential price that we pay for the modeling of the vapor — liquid discontinuous transition with a continuous mathematical function. Let us zoom in on Figure 9.1, as shown in Figure 9.3.
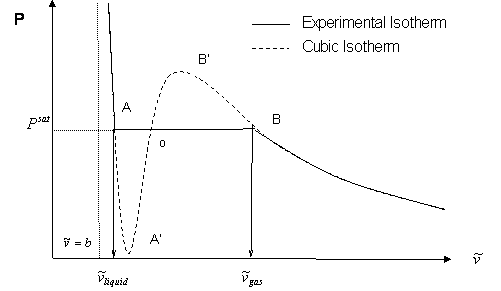
There are several features of the S-shaped behavior that should be noted.
- The S-shaped transition represents the zone where gas and liquid coexist in equilibrium for a pure substance; hence, such a behavior will show up whenever a cubic equation of state is used for predictions at temperatures below critical conditions (sub-critical conditions).
- Physically, changes in pressure and changes in volume in a fluid must have different signs in any isothermal process, such that:
This requirement is met by the liquid branch, gas branches and sections AA’ and BB’ of the cubic isotherm. Portions AA’ and BB’ have even been realized experimentally for metastable conditions, i.e., conditions of fragile or weak stability. However, changes of pressure and volume have the same sign in portion A’B’; consequently, this portion of the cubic isotherm is regarded as meaningless and unphysical. - Point A’ and B’ are the minimum and maximum values of the metastable behavior represented by the S-shaped curve. The saturation pressure (Psat) will naturally lie between these two extremes. Graphically, Psat can be attained as the pressure that make the areas AoA’ and BoB’ equal. This equal-area rule is known as the Maxwell principle. Similarly, we can also determine the saturation condition as the pressure where fugacity — a thermodynamic property we will be studying later — is equal both at the liquid and vapor branches.
- It is not impossible for section AA’ of the cubic isotherm to reach negative pressures (i.e., PA’ < 0). This should not be of any concern to us because we are seldom interested in such metastable behavior. In fact, once Psat is determined, most practical applications call for cleaning up the cubic isotherm and suppressing areas AoA’ and BoB’. In this case, we are left with liquid branch, the discontinuity AB’ at Psat, and the gas branch; just as the experimental isotherm would look.
- The most crucial implication of the S-shaped curve is that the cubic equation will certainly produce three distinct real roots for molar volume (or compressibility factor, if it is the case.) This will always be the case as long as you are making a prediction within the S-shaped curve (PA’ < P < PB’ ; T < Tc). At the vapor-liquid discontinuous transition — i.e., at the intercept of the cubic isotherm with the saturation pressure, Psat, at the given temperature — we end up with 3 mathematically possible real roots for volume. The extreme points of intersection represent liquid molar volume and gas molar volume respectively, represented as and in Fig. 9.3. The third, middle root, given by point “o”, is always regarded as unphysical and is always discarded, because it belongs to the path A’B’.