The principle of Corresponding States (PCS) was stated by van der Waals and reads: “Substances behave alike at the same reduced states. Substances at same reduced states are at corresponding states.” That is,

“Substances at corresponding states behave alike.”

Reduced properties are used to define corresponding states. Reduced properties provide a measure of the “departure” of the conditions of the substance from its own critical conditions and are defined as follows:

$$P_r=\frac{P}{P_c}$$ (8.1a)

$$T_r=\frac{T}{T_c}$$ (8.1b)

$${\stackrel{-}{v}}_r=\stackrel{-}{\frac{v}{{\stackrel{-}{v}}_c}}$$ (8.1c)

If P_r = T_r = v_r = 1, the substance is at its critical condition. If we are beyond critical conditions, T_r > 1, P_r > 1 and v_r > 1. By the same token, if all the conditions are subcritical, T_r < 1, P_r < 1 and v_r < 1. Critical conditions become the scaling factor by which substances can be compared among each other in terms of their “departure from criticality” or reduced properties.

The PCS says that all gases behave alike at the same reduced conditions. That is, if two gases have the same “relative departure” from criticality (i.e., they are at the same reduced conditions), the corresponding state principle demands that they behave alike. In this case, the two conditions “correspond” to one another, and we are to expect those gases to have the same properties.

The Corresponding State Principle can be derived from vdW EOS. If we recall,

$$\left(P+\frac{a}{\stackrel{-}{v}}\right)\stackrel{-}{(v}-b)=RT$$ (8.2a)

where:

$$\alpha =\frac{24}{64}\frac{R^2{T}^2{}_c}{P_c}$$ (8.2b)

$$b=\frac{R{T}_c}{8P_c}$$ (8.2c)

We defined the reduced conditions as:

$$P_r=\frac{P}{P_c}{T}_r=\frac{T}{T_c}{\stackrel{-}{v}}_r=\frac{\stackrel{-}{v}}{{\stackrel{-}{v}}_c}$$ (8.3)

If we substitute all this into vdW EOS,

$$\left(P_c{P}_r\frac{27R^2{T}_c^2}{64P_c{\stackrel{-}{v}}^2{\stackrel{-}{v}}^2{}_r}\right)\left({\stackrel{-}{v}}_c{\stackrel{-}{v}}_r-\frac{R{T}_c}{8P_c}\right)=R{T}_c{T}_r$$ (8.4)

Simplifying the expression, and employing the expressions:

$${\stackrel{-}{v}}_c=\frac{3R{T}_c}{8P_c}$$ (8.5a)

$$Z_c=3/8=0.375$$ (8.5b)

We get:

$$\left(P_r\frac{3}{{\stackrel{-}{v}}_r^2}\right)(3{\stackrel{-}{v}}_r-1)=8T_r$$ (8.6)

Equation (8.6) is the reduced form of vdW EOS. See how this equation is “universal”. It does not care about which fluids we are talking about. Just give it the reduced conditions “P_r, T_r” and it will give you back v_r — regardless of the fluid. Hence, if you compute v_r for a certain fluid by entering P_r and T_r for that fluid into vdW reduced EOS (equation 8.6), you will compute the same v_r, for any other fluid at the same conditions of P_r and T_r. There is no other possibility. Strictly speaking, van der Waals’ Corresponding States Principle reads: “fluids at the same reduced pressures and temperatures have the same reduced volume.” This is how van der Waals discovered the Principle of Corresponding States. As long as two gases are at corresponding states (same reduced conditions), it does not matter what components you are talking about, or what is the nature of the substances you are talking about; they will behave alike.

The critical point provides the perfect scaling for the application of the corresponding state principle because of the existence of the criticality conditions. In fact, equation (7.13) [Module 7] makes the application of corresponding states possible for equations of state.

$${\left(\frac{\alpha P}{\stackrel{-}{\partial v}}\right)}_{P_c,T_c}={\left(\frac{{\alpha }^{2}P}{{\stackrel{-}{\partial v}}^2}\right)}_{P_c,T_c}=0$$ (7.13)

Indeed, for us to arrive at equation (8.6), we needed to use equations (8.2) — which in turn were the outcome of the application of the criticality conditions to van der Waals’ equation of state. As a result, gases that have the same relative departure from their own critical condition have the same properties.

What is the use of this principle? Basically, it is used for thermodynamic correlations — its most powerful application. Most thermodynamic correlations have been made viable and general because of the application of the principle of corresponding states. An excellent example is the popular Z-chart of Standing and Katz, shown in Figure 8.1. In fact, most of the correlations that we use in thermodynamics are based on this principle. This explains why “P_r” and “T_r” so often appear in thermodynamic correlations. The main reason for using “P_r” and “T_r” is to obtain the most generalized correlation possible, so that it is suitable for use with most substances.

Figure 8.1: Standing-Katz Compressibility Factor Chart
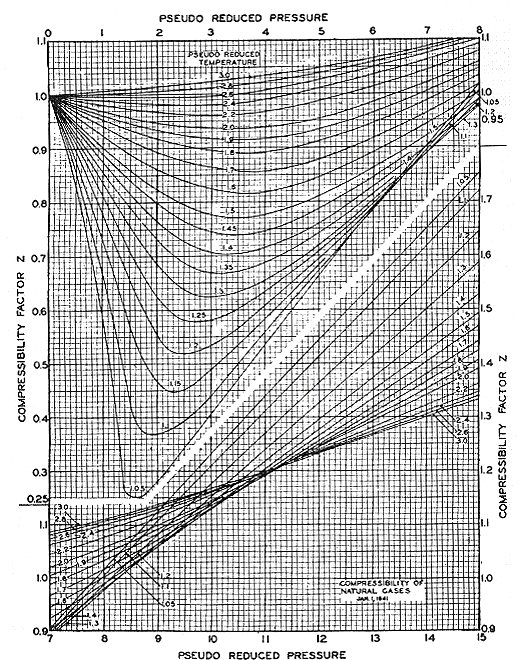
(Reference: Standing and Katz, Trans. AIME, 1942)

It is important to point out that the PCS that we have just discussed was originally outlined by van der Waals. In reality, it is the simplest version of the principle of corresponding states, and it is referred to as the two-parameter PCS. This is because it relies on two parameters (reduced pressure and temperature) for defining a “corresponding state.”

With the passing of time, more accurate PCS formulations have made use of more than two parameters. For instance, the three-parameter PCS affirms that two substances are in corresponding states not only when they are at the same reduced conditions (reduced pressure and temperature), but also when they have the same “acentric factor” value. In any case, the general statement of PCS remains untouched:

“Substances at corresponding states behave alike.”

What makes the difference is the definition of “what a corresponding state is.”

The acentric factor “w” is a concept that was introduced by Pitzer in 1955, and has proven to be very useful in the characterization of substances. It has become a standard for the proper characterization of any single pure component, along with other common properties, such as molecular weight, critical temperature, critical pressure, and critical volume.

Pitzer came up with this factor by analyzing the vapor pressure curves of various pure substances. From thermodynamic considerations, the vapor pressure curve that we studied in our first modules for pure components can be mathematically described by the Clausius Clapeyron equation:

$$\frac{1}{P}\frac{dP}{dT}=\frac{\Delta {\tilde{H}}_{vap}}{RT\Delta Z}$$ (8.7)

The use of the integrated version of equation (8.7) is very common for the mathematical fitting of vapor pressure data. The integrated version of equation (8.7) shows that the relationship between the logarithm of vapor pressure and the reciprocal of absolute temperature is approximately linear. That is, in terms of reduced conditions, vapor pressure data approximately follows a straight line when plotted in terms of “logP_r” versus “1/Tr”, or, equivalently:

$${\log }_{10}{P}_r=a\left(\frac{1}{T_r}\right)+b$$ (8.8)

If the two-parameter corresponding state principle were to hold true for all substances, the parameters “a” and “b” should be the same for all substances. That is, all vapor pressure curves of all imaginable substances should lie on top of each when plotted in terms of reduced conditions. Stated in another way, if the plot is of the form “logP_r” versus “1/T_r”, all lines should show the same slope (a) and intercept (b).

The bad news is that, as you may imagine, this is not always true. Vapor pressure data for different substances do follow different trends. The good news is that some gases follow the expected trend. Which are they? The noble gases. Noble gases (such as Ar, Kr and Xe) happen to follow the two-parameter corresponding states theory very closely. Hence, they yield themselves amenable to acting as a reference to evaluate “compliance” with the two-parameter equation of state.

Pitzer wanted to come up with a reliable way of quantifying the deviation of substances with respect to two-parameter corresponding state predictions. He decided to use noble gases as the base for comparison. Analyzing vapor pressure data for noble gases, Pitzer showed that a value of logP_r = – 1 was achieved at approximately T_r = 0.7. So, BINGO! There you are! He thought: if the vapor pressure data of a substance show that logP_r = – 1 at T_r = 0.7, it behaves as the noble gases and thus complies with the two-parameter corresponding states. If not, we are to compute the difference:

$$Difference=-{\log }_{10}\left(P_r\right)T_{r=0.7}-1$$ (8.9)

Pitzer called this difference the “acentric factor, $\omega$ ” of the substance. Noble gases, being the reference themselves, have an acentric factor value of zero ($\omega$=0). Substances with an acentric factor of zero are called “simple” substances. The acentric factor is said to be a measure of the non-sphericity (acentricity) of the molecules. Therefore, the three-parameter corresponding state theory of Pitzer reads: “Fluids that have the same value of $\omega$ will behave alike at the same conditions of reduced pressure and temperature.”

Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.

Please note:

• Your answers must be submitted in the form of a Microsoft Word document.
• Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
• The due date for this assignment will be sent to the class by e-mail in Canvas.
• Your grade for the assignment will appear in the drop box approximately one week after the due date.
• You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears (this needs update)