Cubic EOS and Their Behavior (II)
Module Goals
Module Goal: To demonstrate thermodynamic quantification using modern cubic EOS.
Module Objective: To highlight the most often used cubic EOS.
Multiple Roots and Cubic Behavior
It comes as no surprise that cubic equations of state yield three different roots for volume and compressibility factor. This is simply because they are algebraic equations, and any nth order algebraic equation will always yield “n” roots. However, those “n” roots are not required to be distinct, and that is not all: they are not required be real numbers, either. A quadratic expression (n = 2) may have zero real roots (e.g., x2 + 1 = 0); this is because those roots are complex numbers. In the case of cubic expressions (n = 3), we will either have one or three real roots; this is because complex roots always show up in pairs (i.e., once you have a complex root, its conjugate must also be a solution.) In our case, and because we are dealing with physical quantities (densities, volumes, compressibility factors), only real roots are of interest. More specifically, we look for real, positive roots such that in the case of molar volume and in the case of compressibility factor.
In a cubic equation of state, the possibility of three real roots is restricted to the case of sub-critical conditions (T < Tc), because the S-shaped behavior, which represents the vapor-liquid transition, takes place only at temperatures below critical. This restriction is mathematically imposed by the criticality conditions. Anywhere else, beyond the S-shaped curve, we will only get one real root of the type . Figure 10.1 illustrates this point.
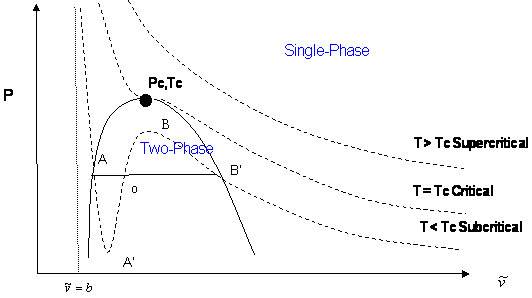
Let us examine the three cases presented in Figure 10.1:
- Supercritical isotherms (T > Tc): At temperatures beyond critical, the cubic equation will have only one real root (the other two are imaginary complex conjugates). In this case, there is no ambiguity in the assignment of the volume root since we have single-phase conditions. The occurrence of a unique real root remains valid at any pressure: any horizontal (isobaric) line cuts the supercritical isotherm just once in Figure 10.1.
- Critical isotherm (T = Tc): At the critical point (P = Pc), vapor and liquid properties are the same. Consequently, the cubic equation predicts three real and equal roots at this special and particular point. However, for any other pressure along the critical isotherm (P < Pc or P > Pc,) the cubic equation gives a unique real root with two complex conjugates.
- Subcritical isotherm (T < Tc): Predictions for pressures within the pressure range for metastability (PA’ < P < PB’) or for the saturation condition (P = Psat) will always yield three real, different roots. In fact, this is the only region in Figure 10.1 where an isobar cuts the same isotherm more than once. The smallest root is taken as the specific volume of the liquid phase; the largest is the specific volume of the vapor phase; the intermediate root is not computed as it is physically meaningless. However, do not get carried away. Subcritical conditions will not always yield three real roots of the type . If the pressure is higher than the maximum of the S-shaped curve, PB, we will only have one (liquid) real root that satisfies . By the same token, pressures between 0 < P < PA’ yield only one (vapor) root. In the case of PA’ being a negative number, three real roots are to be found even for very low pressures when the ideal gas law applies. This can be seen in Figure 10.1 as well. The largest root is always the correct choice for the gas phase molar volume of pure components.
Most of these considerations apply to the cubic equation of state in Z (compressibility factor). The most common graphical representation of compressibility factor is the well-known chart of Standing and Katz, where Z is plotted against pressure. Standing and Katz presented their chart for the compressibility factor (Z) of sweet natural gases in 1942. This chart was based on experimental data. Graphical determination of properties was widespread until the advent of computers, and thus the Standing and Katz Z-chart became very popular in the natural gas industry. Typical Standing and Katz charts are given for high temperature conditions (T > Tc or Tr > 1). Figure 10.2, using a cubic equation of state for a pure gas, presents the qualitative behavior of the solution of Z versus pressure. Isotherms (T > Tc) show the typical qualitative behavior we are accustomed to seeing in the Standing and Katz chart. Cases T < Tc (Tr < 1) are not as familiar to us, as they were not considered by Standing and Katz. For such isotherms, it is clear that you come up with two values of Z (liquid, gas) at saturation conditions.
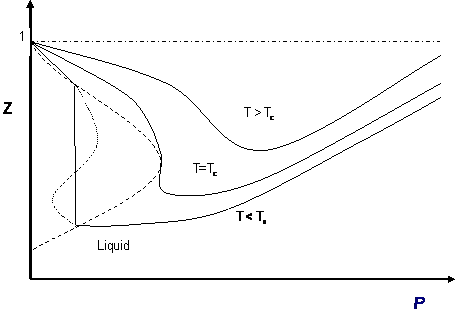
Modern Cubic EOS
At this point, we have a couple of comments on the cubic behavior that the pioneer work of vdW introduced to the field of equations of state. First, we can say that the vdW cubic behavior is qualitatively reasonable; and second, we can say that it is capable of describing the continuity between liquid and vapor. Nevertheless, vdW cubic EOS has been proven not to be quantitatively suitable for most engineering purposes. Certainly, it yields unacceptable errors for the quantitative prediction of densities and any other related thermodynamic property. However, all of the development in the field of phase behavior that has been achieved today is due to the work of van der Waals. Although his own equation is seldom used because of its lack of accuracy, his principles are still the foundations of the current developments. vdW concepts were so far reaching that he won the Nobel Prize for his equation.
The truth is that van der Waals’ accomplishment in 1873 triggered a tremendous effort among scientists to make modifications to his EOS which would remove from it large disagreements with experimental data. This effort has not yet ceased today and is not likely to stop in the near future. Much of this endeavor has focused on how to better model the attractive parameter “a” and the repulsive term “b”, with the hope that we can get better quantitative predictions. Naturally, the qualitative cubic-nature of vdW’s original EOS is always preserved, and hence all subsequent refinements belong to the same family of modified-van-der-Waals equations of state. We refer to vdW EOS and all its descendents as cubic equations of state, because, as we have said, they take a cubic form when expressed in terms of volume or compressibility factor and are explicit in pressure.
It is fair to claim that modern cubic EOS started to make a difference when a temperature dependency was introduced to the attractive parameter “a”. Interestingly enough, van der Waals was convinced that the parameters “a” (and even “b”) of his equation of state were not necessarily constants and suggested that, indeed, some dependency on temperature could be found. A very interesting discussion on this, from van der Waals himself, is found in the lecture speech that he offered during his acceptance of the Nobel Prize in Physics, in 1910, for his work on the continuity of vapor and liquid. This speech and the biography of this great physicist, Johannes Diderik van der Waals (1837-1923), can be found in the web resources of the Nobel Prize organization.
The most popular cubic EOS, which time has proven to be most reliable, are:
- Redlich-Kwong EOS,
- Soave-Redlich-Kwong EOS (very popular among chemical engineers),
- Peng-Robinson EOS (very popular among petroleum and natural gas engineers).
Keep in mind that, once you have an EOS, you can derive virtually any property of the fluid.
Redlich-Kwong EOS (1949)
vdW cubic equation of state had to wait almost 100 years before a real, successful improvement was introduced to it. As we stated before, this progress occurred once researchers committed themselves to finding the empirical temperature dependency of the attraction parameter “a” proposed by van der Waals. In contrast, very little attention has been paid to modifying the parameter “b” for co-volume. It makes a lot of sense that “b” would not be modified by temperature, because it represents the volume of the molecules, which should not be affected by their kinetic energy (measured in terms of temperature).
The very first noteworthy successful modification to the attraction parameter came with the publication of the equation of state of Redlich-Kwong in 1949. Redlich and Kwong revised van der Waals EOS and proposed the following expression:
(10.1)
Notice that the fundamental change they introduced was to the functional form of (equation 7.8, Module 7). Additionally, they introduced the co-volume “b” into the denominator of this functional form.
The important concept here is that the attraction parameter “a” of van der Waals needed to be made a function of temperature before any cubic EOS was able to do a better job of quantitatively matching experimental data. This was a realization that vdW himself had suggested, but no actual functional dependency had been introduced until the Redlich-Kwong EOS.
We know what follows at this point. To come up with an expression for “a” and “b” of equation (10.1), we apply the criticality conditions to this EOS. As we recall, imposing the criticality conditions allows us to relate the coefficients “a” and “b” to the critical properties (Pc, Tc) of the substance. Once we have done that, we obtain the definition of “a” and “b” for the Redlich-Kwong EOS,
(10.2a)
(10.2b)
This EOS radically improved, in a quantitative sense, the predictions of vdW EOS. We now recall that vdW-type equations are cubic because they are cubic polynomials in molar volume and compressibility factor. It comes as no surprise then, that we can transform equation (10.1) into:
(10.3)
and, by defining the following parameters,
(10.3a)
(10.3b)
and introducing the compressibility factor definition , we get:
(10.4)
We may also verify the two-parameter corresponding state theory by introducing equations (10.3) and (10.2) into (10.4),
(10.5)
In equation (10.5) we can observe the same thing that we saw with vdW EOS: gases at corresponding states have the same properties. Equation (10.5) is particularly clear about it: any two different gases at the same Pr, Tr condition have the same compressibility factor.
Just as any other cubic equation of state, equations (10.1) through (10.5), as they stand, are to be applied to pure substances. For mixtures, however, we apply the same equation, but we impose certain mixing rules to obtain “a” and “b”, which are functions of the properties of the pure components. Strictly speaking, we create a new “pseudo” pure substance that has the average properties of the mixture. Redlich-Kwong preserved the same mixing rules that vdW proposed for his EOS:
(10.6a)
(10.6b)
Naturally, Redlich and Kwong did not have the last word on possible improvements to the vdW EOS. The Redlich-Kwong EOS, as shown here, is no longer used in practical applications. Research continued and brought with it new attempts to improve the RK EOS. After more than two decades, a modified RK EOS with very good potential was developed. The Soave-RK EOS was born.
Soave-Redlich-Kwong EOS (1972)
In 1972, Soave proposed an important modification to the RK EOS — or shall we say, a modification to vdW EOS. Between the time of vdW EOS and Redlich-Kwong’s, a new concept for fluid characterization was being discussed. Pitzer had introduced the concept of acentric factor in 1955.
All modifications to the vdW EOS had focused on the temperature dependency of the attractive parameter. Soave expanded this by proposing a two-variable dependency for “a”:
(10.7)
It was the first time that “a” was expressed not only as a function of temperature, but also as a function of the shape (sphericity) of the molecules (through w, Pitzer’s acentric factor). As we recall, Pitzer’s acentric factor is a measure of the configuration and sphericity of the molecule. It can also be seen as a measure of the deformity of the molecule.
The Soave-Redlich-Kwong EOS is given by the expression:
(10.8a)
Like all cubic equations of state, the SRK EOS is also explicit in pressure. Notice, for example, how the SRK EOS readily becomes:
(10.8b)
where,
(10.8c)
The influence of acentric factor and temperature on the attractive term is introduced now through “a”. What do we do next? We apply the criticality conditions to equation (10.8b). Notice that expression (10.8c) becomes unity at Tr=1, throughout the critical isotherm. We obtain:
(10.9a)
(10.9b)
Now we show the cubic form (in compressibility factor) of Soave-Redlich-Kwong EOS. Defining,
(10.10a)
(10.10b)
we are able to obtain:
(10.11)
For mixtures, Soave proposed a “little” modification to the mixing rules with which we have dealt with so far by introducing the use of “binary interaction parameters” (kij):
(10.12a)
(10.12b)
The use of binary interaction parameters (kij) generated a lot of resistance upon their first introduction. This is because there is no analytical, science-based derivation that justifies their existence. Nowadays, they are regarded just as they are, empirical factors used to tune equations of state and make them match experimental data for mixtures. This has become the heuristic justification for their existence: with them, EOS can do a better job of matching experimental data. Heuristically speaking, they are a measure of interaction between a pair of dislike molecules. Based on this “definition,” their value is zero for pairs of molecules that are alike. Actually, this is no more than a mathematical requirement in order for equation (10.12a) to give when j=i. The determination of kij is based on experimental data from binary systems; “kij” results from the value that allows the given equation of state (through the expression in 10.12a) to yield the closest match. These values are assumed to be constant (and so are used) when the same two components are part of a more complex multi-component mixture.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:
- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
-
An engineer is seeking your advice on which EOS he should use to model various hydrocarbon mixtures he is dealing with. He has access to a program that provides him with several options for different cubic EOS. He presents you with the following list:
-
A sweet natural gas from Nigeria
- A sour natural gas (high CO2, H2S contents)
- Flue gas
-