Engineering Applications (I)
Module Goals
Module Goal: To highlight some of the important applications of phase behavior in production operations.
Module Objective: To describe the use of flash calculations in separator optimization and gas-condensate reservoir description.
Introduction: Phase Behavior as the Quintessential Tool
Optimal design and the safe and efficient operation of hydrocarbon production handling and processing systems strongly depends on accurate knowledge of fluid phase behavior. In fact, in contrast with other disciplines, the practice of petroleum and natural gas engineering centers around understanding the interaction between fluids and various environments, including the reservoir, pipeline, separator, pumps and compressors, etc. Another distinguishing characteristic is the complexity of the fluid involved here — petroleum. Whereas, for instance, mechanical engineers deal mainly with water (single-component system) and air (considered ideal for most applications), here we are dealing with complex hydrocarbon mixtures where the composition dependence of thermophysical properties is very strong.
Another complication is the wide range of pressures and temperatures associated with the processes of interest, from ultralow temperatures (LNG) to as much as 210 °F and pressures ranging from atmospheric to several thousand psia. Within these ranges, the fluid can transcend the three principal phases, namely gas, liquid, and solid, and worse yet, any combination of these.
The combination of the complex mixtures involved, the wide compositional variability from reservoir to reservoir, from system to system, and the wide range of pressures and temperatures to which systems are often subjected (e.g. a pipeline) make the phase behavior of these systems a very challenging undertaking. Unless one has a good descriptive and predictive understanding of the fluid’s phase behavior, their interactions and responses cannot be successfully described.
In these last two modules of the course, we will examine some of the applications of our current knowledge of phase behavior and thermodynamics in Petroleum and Natural Gas Engineering. The message we would like to provide is very simple: the phase behavior of the hydrocarbon system must be fully grasped in order to fully understand the responses of condensate and natural gas systems and optimize their performance. For example, maximization of condensate yield is virtually impossible without the tools for accurate prediction of just how much liquid will exist under given conditions of pressure, temperature and composition. Therefore, having advanced predictive tools for the characterization of hydrocarbon phase behavior with the highest accuracy possible is the key to mastering the economics of hydrocarbon systems. In the next sections, we will explore some specific areas where the mastering of phase behavior concepts is a must.
Design and Optimization of Separators
Once oil and gas are brought to the surface, our main goal becomes that of transportation of the oil and gas from the wellhead to the refinery (for final processing). All equipment and processes required to accomplish this are found at the surface production facility. Hence, all surface production starts right at the wellhead. Starting at the wellhead, the complex mixture of produced fluids makes its way from the production tubing into the flow line. Normally, many wells are drilled to effectively produce the hydrocarbons contained in the field. From each of these wells emerge one or more flow lines depending on how many layers are being produced simultaneously. Depending on the physical terrain of the area and several other environmental factors, each of the flow lines may be allowed to continue from the wellhead to a central processing facility commonly referred as a production platform or a flow station, which then carries the fluids to the production platform. The combination of the wellhead, the flow lines, bulk headers, valves and fittings needed to collect and transport the produced fluid to the production platform is referred to as the gathering system.
The gathered fluids must be processed to enhance their value. First of all, fluids must be separated into their main phasial components - namely, oil, water, and natural gas. The separation system performs this function. For this, the system is usually made up of a free water knock-out (FWKO), flow line heater, and oil-gas (two-phase) separators. We will be looking at the design of this last component.
The physical separation of these three phases is carried out in several steps. Water is separated first from the hydrocarbon mixture (by means of the FWKO), and then the hydrocarbon mixture is separated into two hydrocarbon phases (gas and oil/condensate). A successful hydrocarbon separation maximizes production of condensate or oil, and enhances its properties. In field applications, this is accomplished by means of stage separation. Stage separation of oil and gas is carried out with a series of separators operating at consecutively reduced pressures. Liquid is discharged from a higher-pressure separator into the next-lower-pressure separator. The purpose of stage separation is to obtain maximum recovery of liquid hydrocarbons from the fluids coming from the wellheads and to provide maximum stabilization of both the liquid and gas effluents.
Surface Production Facility: The physical installation where fluids coming from the wellhead are separated into three main constituents: water, oil, and natural gas.

Usually it is most economical to use three to four stages of separation for the hydrocarbon mixture. Five or six may payout under favorable conditions, when — for example — the incoming wellhead fluid is found at very high pressure. However, the increase in liquid yield with the addition of new stages is not linear. For instance, the increase in liquids gained by adding one stage to a single-stage system is likely to be substantial. However, adding one stage to a three or four-stage system is not as likely to produce any major significant gain. In general, it has been found that a three-stage separating system is the most cost-effective. Figure 20.2 shows this typical configuration.
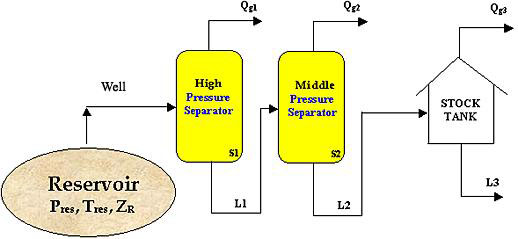
Under the assumption of equilibrium conditions, and knowing the composition of the fluid stream coming into the separator and the working pressure and temperature conditions, we could apply our current knowledge of VLE equilibrium (flash calculations) and calculate the vapor and liquid fractions at each stage. However, if we are looking at designing and optimizing the separation facility, we would like to know the optimal conditions of pressure and temperature under which we would get the most economical profit from the operation. In this context, we have to keep in mind that stage separation aims at reducing the pressure of the produced fluid in sequential steps so that better and more stock-tank oil/condensate recovery will result.
Separator calculations are basically performed to determine:
- Optimum separation conditions: separator pressure and temperature
- Compositions of the separated gas and oil phases
- Oil formation volume factor
- Producing Gas-Oil ratio
- API gravity of the stock tank oil
Let us look at the case of three-stage separation. In general, temperature conditions in the surface separation facility are very much determined by the atmospheric condition and incoming stream temperatures. As for pressures, the very first separator pressure is controlled by the gathering lines coming from well heads, thus there is not much room for playing with pressure in the first separator. The same arguments are valid for the last stage of separation (stock tank), which usually operates at atmospheric conditions. Therefore, we are only left with the middle separator for optimization.
As it turns out, the key to designing a three stage separation system is finding the optimum pressure at which to operate the second separator. The question that we would answer is “what is the pressure that will result in the best quality liquid going out of the stock tank for sales?” We do not want to do this empirically. This is, we do not want to play with the second stage separator pressure in the field, until we ultimately find the optimum condition. What we can do, using our phase behavior knowledge, is to find this optimum middle stage pressure applying our understanding of VLE equilibrium.
Figure 20.3 shows the typical effect of playing with the middle separator pressure on the quality and quantity of produced oil/condensate at the stock tank. Quality and quantity are measured in terms of properties, such as API and Bo, and the overall GOR at the separation facility.
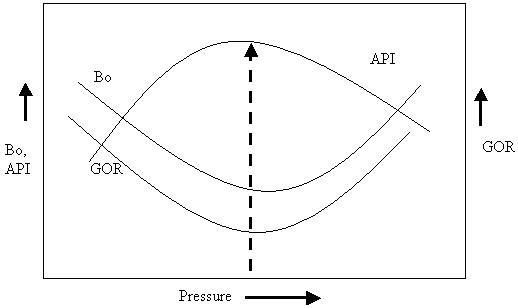
The optimum value of pressure for the middle stage is the one that produces the maximum liquid yield (by minimizing GOR and Bo) of a maximum quality (by maximizing stock-tank API gravity). The smaller the value of GOR and Bo, the larger the liquid yield. The higher the API gravity of the stock-tank fluid, the more profitable its commercialization. From Figure 20.2, we see that this condition is found at neither extreme (low/high) values of middle stage pressure. There is, in fact, an optimal value for middle stage pressure. This is the value we are looking for.
The Phase Behavior model that we have described throughout these series of lectures provides the basic framework for the type of calculations required here. Additionally, we discussed how API and Bo can be calculated using the output of the phase behavior model. While doing the calculations for a 3-stage separating system, keep in mind that we have minimal control over feed pressure, as we do not want to inhibit the well (high-pressure separator). We do not control the sales line pressure (stock-tank pressure) either. The control that we do have is the operating pressure of the middle separator.
Recall that finding the optimum pressure calls for, in part, finding the minimum gas to oil ratio (GOR, SCF/STB). We are dealing, in this case, with total GOR. The total GOR is the cumulative amount of gas from all three separators divided by the amount of liquid/condensate leaving the stock tank. During our discussion on Bo-calculations, we called “nst” the moles of liquid leaving the stock tank per mole of feed entering the separation facility. This number can be obtained by sequentially flashing 1 lbmol of feed through each of the separation stages. Recalling the definition of GOR,
where:
[basis: 1 lbmol of feed]
Therefore,
Usually, the stock tank is considered to operate at standard conditions (psc, Tsc). Now you are ready to make your own surface separation design!
Compositional Modeling of Gas-Condensate Reservoirs:The Zero-dimensional Approach
Phase behavior is relevant to every aspect of petroleum and natural gas engineering. According to the complexity of the reservoir fluid phase behavior, reservoir modeling is classified under two distinct groups: black-oil simulation and compositional simulation. ; Often times, it is safe to assume that reservoir fluid behavior is only a function of pressure and independent of composition. This simplified behavior is typical of “black-oil” systems. In this case, reservoir hydrocarbon fluids are assumed to be comprised of two components, namely oil and gas. The model allows for certain amount of gas to be in solution with the oil at reservoir conditions. The amount of dissolved gas increases with, and is a sole function of, pressure for conditions below the bubble point. Above the bubble point pressure, the oil-component carries all the available gas in the reservoir, and a “variable bubble point” algorithm is usually implemented to predict conditions for the release of the dissolved gas. For this “black-oil” simplified model to be valid, actual oil and gas phases should maintain a fixed-composition throughout the process simulated in the reservoir. In certain cases, the assumption of fixed oil and gas composition is no longer valid: for instance, depletion of gas-condensate reservoirs and volatile-oil reservoirs, and processes that aim at the vaporization or miscible flooding of the in-situ fluids by fluid injection. More complex fluid behavior requires treating all hydrocarbon phases as nc-component mixtures and thus performing a “compositional simulation.”
Although the need for taking compositional dependence of thermodynamic and hydrodynamic parameters into account in reservoir description has been recognized for a long time, the actual implementation has not been realized until relatively recently. One of the main reasons is due to the lack of simple and reliable methods of predicting phase behavior under the conditions of interest. Two things have happened within the last three decades that have changed the situation: They are (1) the availability of fast and relatively inexpensive computational power to carry out the great number of calculations involved and (2) the development of samples and fairly good equations of state.
Simply put, a compositional reservoir simulator is a dynamic integration of the fluid dynamic porous media model and the phase behavior model, neither of which is subordinated to the other. In fact, in the early days of compositional reservoir simulation, a non-dynamic integration of these two was the norm. The more recent models actually attempt a full dynamic integration. The need for integration had been recognized earlier particularly for gas condensate reservoir, gas cycling processes, and volatile oil systems.
Early developments in reservoir engineering analysis relied on zero-dimensional or tank material balances for the evaluation and forecasting of reservoir performance. In 1936, Schilthuis devised what we now regard as the classical material balance equation. Schilthuis-type material balances are only valid for black-oil systems and are not applicable for reservoir fluids with complex behavior such as gas condensates and volatile oils. Compositional considerations were incorporated into zero-dimensional modeling in the decade of 1950’s with the works of Allen and Row (1950), Brinkman and Weinaug (1957), Reudelhuber and Hinds (1957), Jacoby and Berry (1957), and Jacoby et al. (1959). These can be regarded as the first generation of compositional simulators. Even though zero-dimensional simulations have been largely overthrown by more sophisticated numerical simulation techniques, they are still considered the most simple and fundamental tool available for the analysis of reservoir performance.
The zero-dimensional models make two principal assumptions. The first is to basically ignore the two-way coupling between fluid’s thermophysical properties and the hydrodynamic characteristics. The reservoir is treated as a perfectly mixed tank reactor with uniform properties. We assume no dimensions, and that one single value of pressure and temperature describes the average behavior of the entire reservoir. The second assumption is to neglect the hydrodynamic interactions between the flowing gas and liquid phases. In other words, the zero-dimensional compositional model relies on phase behavior as the most crucial effect controlling the description of recovery performance.
There is no doubt that significant insights, albeit qualitative, are provided by these studies. Zero-dimensional modeling provides a less expensive tool for the engineer to gain some insight into the expected performance of a gas condensate reservoir under depletion. Sometimes we spend a great deal of time dealing with the numerics of the dimensional compositional simulators, and we may forget that phase behavior is the single most important constituent of the depletion performance of, for instance, gas-condensate systems. Nevertheless, the reservoir engineer must keep in mind that this type of analysis does not provide the most accurate reservoir description. For instance, the effect of heterogeneities on reservoir performance cannot be studied with a zero-dimensional model. Again, the goal is to take a look at the qualitative insights that fluid PVT behavior can provide us.
The typical depletion sequence that a zero-dimensional compositional simulator follows is described below. This classical analysis treats gas condensate performance as constant volume depletion (CVD) in a PVT cell. The ultimate output of the model is basically comprised of GOR prediction and the compositions of the gas and condensate surface effluents. We start with a single-phase gas reservoir fluid, of a known composition, at an initial reservoir pressure and temperature. We flash this fluid several times through a series of pressure depletion stages until abandonment conditions are found. Reservoir volume is kept constant throughout the depletion process.
The typical depletion sequence that a zero-dimensional compositional simulator follows are listed below:
- Calculate the density and molecular weight of the initial reservoir fluid. With this information, and knowing the initial reservoir volume (Vti), calculate the initial amount of gas in place (lbmols). An alternative approach is to start with a fixed amount of lbmols of reservoir fluid, and calculate the corresponding initial reservoir volume (Vti). We assume a volumetric reservoir and thus the initial reservoir volume (Vti) is kept constant throughout the calculations.
- Using the reservoir fluid composition, distribute the initial moles of reservoir fluids into components, and store such quantities for material balance accounting.
- Depletion step: Lower the reservoir pressure by a given amount (typically, 200 psi). Flash the reservoir fluid at the new pressure, calculate amount of moles in the gas and liquid phases (“GasT” and “LiqT”) and the densities and molecular weights of each of the phases at the new condition.
- Expansion: With molecular weight, density, and total molar amount of each of the phases, calculate the new total volume that the fluids occupy at the new condition (Vexp).
-
Calculate the excess volume of fluids, taking the difference between the new volume upon expansion (Vexp) and the reservoir volume (Vti). This represents the volume of fluid that must have been withdrawn by the well in order to reach the newly imposed pressure condition, i.e.
Vws = Vexp – Vti(20.3) - Calculate the percentage of liquid in the well stream using mobility ratio considerations. Trial and error procedure is necessary for the liquid accounting. The total amount of liquid available upon depletion (LiqT) must be distributed between the wellstream (LiqWS) and the liquid remaining in the reservoir (LiqR). Additionally, the moles of reservoir liquid “LiqR” can be expressed in terms of oil/condensate saturation. Oil saturations define the mobility of the gas and liquid phases. These interrelations are shown below:
(20.4a)(20.4b)(20.4c)(20.4d)
LiqWS is a function of mobility ratio, which is a function of LiqR (through So). As a first guess, take LiqR = LiqT and calculate the corresponding LiqWS. Make new guesses (decreasing the value in every new trial) until the liquid balance in Equation (20.4a) is satisfied.
- Once LiqWS and (Vws)liq are known, obtain the total volume of gas withdrawn from the reservoir by subtracting the liquid volume (Vws)liq from the total wellstream volume (Vws). Express this gas volume in moles using reservoir gas density and molecular weight. Calculate the total number of moles of the wellstream.
- Material Balance Accounting: Calculate the number of moles of each component remaining in the reservoir. To do this: subtract the number of moles leaving the well stream from the number in the reservoir before flashing for each of the components. Calculate the new overall composition of the reservoir fluid.
- Calculate the overall composition of the produced well stream, by mixing the composition of gas and liquid coming along.
- Surface Production Facility: Flash the incoming wellstream composition through the train of separations. Calculate the total amount of gas and liquid leaving the separation facility and GOR. Calculate the percentage of recovery from the reservoir.
- A depletion loop has been completed. Go back to step 3 until abandonment pressure is reached (typically, 600 psia).
- Plot liquid production, gas production, GOR, and recovery from the reservoir as a function of pressure depletion, from initial reservoir conditions to abandonment conditions.
The basic VLE calculations required here can be performed using the Peng-Robinson EOS and equilibrium considerations. Liquid viscosities can be calculated through the Lohrenz, Bray, and Clark correlation, and gas viscosities can be calculated using the Lee-Gonzalez correlation. Fluid densities are obtained directly through the Peng-Robinson EOS.
Action Item
Answer the following problems, and submit your answers to the drop box in Canvas that has been created for this module.
Please note:- Your answers must be submitted in the form of a Microsoft Word document.
- Include your Penn State Access Account user ID in the name of your file (for example, "module2_abc123.doc").
- The due date for this assignment will be sent to the class by e-mail in Canvas.
- Your grade for the assignment will appear in the drop box approximately one week after the due date.
- You can access the drop box for this module in Canvas by clicking on the Lessons tab, and then locating the drop box on the list that appears.
Problem Set
- API, GOR and Bo are the parameters that we use to optimize a train of separators. Speculate on why all three parameters seem to predict the same optimal separator pressure.
- Although zero-dimensional modeling can be used to model behavior of gas-condensate systems, there are some pitfalls in the description. What are these pitfalls? In what cases can we overlook them?