Surface complexation models describe sorption based on surface reaction equilibrium. Similar to aqueous complexation, surface complexation reactions are considered fast reactions and are controlled by reaction thermodynamics.
Surface Configuration of the Solid–Solution Interface
There are three commonly used SCMs, the constant capacitance model (CCM), the diffuse layer model (DLM), and the triple layer model (TLM). These models differ in complexity from the simplest CCM that has three adjustable model parameters, to the most complex TLM that has seven adjustable parameters [Hayes et al., 1991]. The double layers exist in practically all heterogeneous fluid-based systems. Here we introduce the principle and thermodynamics of DLM.
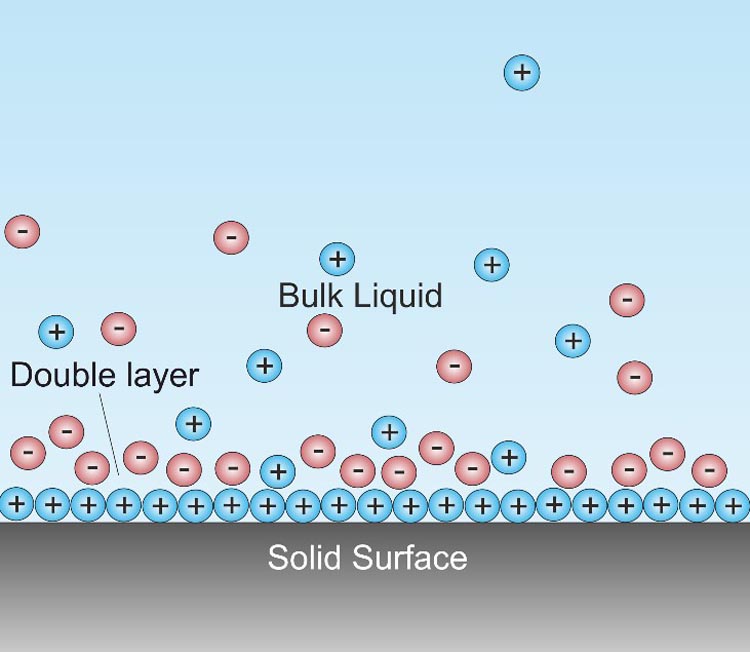
The double layer refers to two parallel layers of charge surrounding the solid surface. The first layer, the surface charge (either positive or negative), comprises ions sorbed onto the solid due to chemical interactions. The second layer (“diffuse” layer) is composed of counter ions attracted to the surface charges via the coulomb force, electrically screening the first layer. The schematic of double layer is shown in Figure 2.
Surface Complexation Reactions
In traditional SCM models, all reactions are considered as at equilibrium. As an example, the surface protolysis reactions, where H+ transfers among chemicals, are given by:
Here the $\equiv S O H$ represents a species or functional group on solid surface. In the first reaction, $\equiv S O H$ gains an H+ and becomes positively charged. In the second reaction, $\equiv S O H$ loses an H+ and becomes negatively charged. The apparent equilibrium constants Kapp describe the relationship between activities of different species, written in the same format as we do for aqueous complexations except now we include activities of solid species.
Similarly, for a metal ion M with a positive charge m, the reactions are represented by:
For an anionic ligand L with a negative charge of l, the reactions are represented by:
In these reactions, $\equiv S O H$ represents a surface site for the sorbent functional group, $\equiv S O H_{2}^{+}, \equiv S O^{-}, \equiv S O M^{(\mathrm{m}-1)}, \equiv(S O)_{2} M^{(\mathrm{m}-2)}, \equiv S O H_{2}^{+}-L^{l-} \text { and } \equiv S O H_{2}^{+}-L H^{(l-1)-}$ are surface complexes, [ ] represents the activity of each species or surface complex, $Mm+$ represents a metal ion of charge m+ and Ll- represents an anionic ligand of charge l−.
Apparent (Kapp) and Intrinsic (Kintr) Equilibrium Constants
The apparent equilibrium constant of surface complexation reactions, Kapp, is an important parameter because it determines the ion partition between aqueous and solid phases. Large Kapp values indicate high affinity of the ions to the solid surface. The relationship between total Gibbs free energy $\Delta G_{\text {tot }}$ and Kapp is as follows:
Here the total Gibbs free energy $\Delta G_{\text {tot }}$ can be further expressed as follows:
Here $\Delta G_{c h e m}^{0}$ is the intrinsic free energy of the chemical reactions at the surface; $\Delta G_{\text {coul }}^{0}$ is the electrostatic or Coulombic term that accounts for the electrostatic interactions:
Here Z is the charge of the ion, F is the Faraday constant (96485 C/mol), $\psi_{0}$ is the average potential of the surface plane (V). Therefore,
Where $K^{\mathrm{int} r}=\exp \left(-\frac{\Delta G_{c h e m}^{0}}{R T}\right)$, R is ideal gas constant $(1.987 \mathrm{cal} /(\mathrm{mol} \cdot \mathrm{K}))$; T is the absolute temperature (K). Take equation (1) as an example,
Where $K_{1}^{\mathrm{int} r}=\frac{\left[\equiv \mathrm{SOH}_{2}^{+}\right]}{[\equiv \mathrm{SOH}]\left[\mathrm{H}_{s}^{+}\right]}$ , Z is the charge of the ion (1 in the case of H+); $\left[H_{s}^{+}\right]$ is H+ activity on the solid surface.
The electrostatic or coulombic effect can be quantified as:
From equation (10), we know that $K_{1}^{\text {int } r}$ and $\psi_{0}$ are needed in order to calculate $K_{1}^{a p p}$. The $K_{1}^{\text {int } r}$ is typically estimated using zero charge extrapolation or using the double extrapolation method as discussed in literature. Under low ionic strength conditions where $\psi_{0} \cong 0$, the intrinsic and apparent constants are equivalent.
Surface sorption site
For different minerals, the number of surface sites differs significantly, depending on their surface properties. The abundance of surface sites is important in determining the total sorption capacity. The concentration of surface sites can be calculated as follows:
Here Csite is the concentration of surface sites (mol/g mineral), ρsites is the surface density of surface hydroxyl sites (mol/m2), Aspecific is the specific surface area (SSA)(m2/g). This equation says that surface site concentration depends on the surface site density and specific surface area. Please note that if you are working with porous media, you will need to calculate the total gram of minerals for surface complexation to get the total number of available sites.
Specific surface area (SSA) and site density values can be determined experimentally from Brunauer -Emmett-Teller (BET) surface area and tritium exchange measurements, respectively. The units of site/nm is often used in literature, where 1 site/nm = 1.66x10-6 mol/m2. Typical values of specific surface area (SSA) and site densities for different types of minerals are listed in Table 1. The total number of surface sites for a particular system (mol) can be calculated by multiplying site density (mol/m2) with SSA (m2/g) and the mineral mass (g). Minerals such as clays tend to have a large surface area and have a large capacity to sorb chemicals.
| Absorbent | SAA (m2/g) | Site density (mol/m2) Strong Site |
Site density (mol/m2) Weak Site |
Reference |
|---|---|---|---|---|
| Goethite | 14.7 | 1.76×10-6 | 3.22×10-6 | (Müller and Sigg, 1992) |
| Kaolinite | 19.5 | 2.20x10-6 | 3.00×10-6 | (Lackovic et al., 2003) |
| Illite | 66.8 | 1.30x10-6 | 2.27x10-6 | (Gu and Evans, 2007) |
| Smectite | 56.4 | 4.77x10-8 | 9.54x10-7 | (Bradbury and Baeyens, 2005) |
Different types of surface sites
Organic and inorganic chemicals are usually sorbed at hydroxyl surface functional groups that are located at the broken bonds and edge sites on minerals with excess negative charges [Baeyens and Bradbury, 1997]. We often classify two kinds of sorption sites: "strong" sites $\left(\equiv \mathrm{S}^{\mathrm{S}} \mathrm{OH}\right)$ and "weak" sites$\left(\equiv \mathrm{S}^{\mathrm{W}} \mathrm{OH}\right)$. "Strong" sites have a low capacity and a high sorption affinity and dominate the uptake of adsorbate at low concentrations. "Weak" sites have a considerably larger capacity however much lower sorption affinity. Table 2 shows reactions and equilibrium constants for U(VI) sorption on ferrihydrite, where FesOH represents strong site with orders of magnitude higher intrinsic equilibrium constants than those of the weak sites $\left(\equiv \mathrm{FE}^{\mathrm{W}} \mathrm{OH}\right)$ (Zheng et al., 2003). In this soil with the presence of ferryhdrate, the site density ratio of weak to strong site is 476:1 (i.e., 0.21% of the total surface sites, 99.79% for the weak sites).
| Reactions | LogKintr |
|---|---|
| $2 \equiv \mathrm{Fe}^{S} \mathrm{OH}+\mathrm{UO}_{2}^{2+} \Leftrightarrow \equiv\left(\mathrm{Fe}^{S} \mathrm{O}\right)_{2} \mathrm{UO}_{2}+2 H^{+}$ | -2.35 |
| $2 \equiv \mathrm{Fe}^{W} \mathrm{OH}+\mathrm{UO}_{2}^{2+} \Leftrightarrow \equiv\left(\mathrm{Fe}^{W} \mathrm{O}\right)_{2} \mathrm{UO}_{2}+2 H^{+}$ | -6.06 |
| $2 \equiv \mathrm{Fe}^{S} \mathrm{OH}+\mathrm{UO}_{2}^{2+}+\mathrm{CO}_{3}^{2-} \Leftrightarrow \equiv\left(\mathrm{Fe}^{S} \mathrm{O}\right)_{2} \mathrm{UO}_{2} \mathrm{CO}_{3}^{2-}+2 \mathrm{H}^{+}$ | 4.33 |
| $2 \equiv \mathrm{Fe}^{\mathrm{W}} \mathrm{OH}+\mathrm{UO}_{2}^{2+}+\mathrm{CO}_{3}^{2-} \Leftrightarrow \equiv\left(\mathrm{Fe}^{W} \mathrm{O}\right)_{2} \mathrm{UO}_{2} \mathrm{CO}_{3}^{2-}+2 H^{+}$ | -0.24 |
Surface charge and point of zero charge (PZC)
Surface complexation leads to surface-charged solid surfaces. Electric surface charges govern characteristic chemical and physical phenomena such as ion exchange, adsorption, swelling, colloidal stability, and flow behavior (Sposito, 1981). It is well known that the surface charges on layered silicates and insoluble oxides depend on the pH of aqueous solutions The pH of the point of zero charge (PZC), where the net total particle charge is zero, is a convenient reference for describing the pH dependence of surface charges. (Appel et al., 2003). When solution pH is above PZC, the solid surface has a negative charge and predominantly exhibits an ability to exchange cations, while the solid surface retains anions (electrostatically) if pH is below its PZC. A list of common substances and their associated PCZs is shown in Table 3.
| Chemical Formula | pHPZC |
|---|---|
| $\text { Kaolinite }$ | 4.6 |
| $\text { Montmorillonite }$ | < 2.5 |
| $\text { Corundum, } \alpha-\mathrm{Al}_{2} \mathrm{O}_{3}$ | 9.1 |
| $\gamma-\mathrm{Al}_{2} \mathrm{O}_{3}$ | 8.5 |
| $\text { alpha- } \mathrm{Al}(\mathrm{OH})_{3}$ | 5.0 |
| $\text { Hematite, } \alpha-\mathrm{Fe}_{2} \mathrm{O}_{3}$ | 8.5 |
| $\text { Goethite, } \alpha \text {-FeOOH }$ | 9.3 |
| $\text { Birnessite, } \delta-\mathrm{MnO}_{2}$ | 2.2 |
| $\mathrm{Fe}(\mathrm{OH})_{3}$ | 8.5 |
| $\text { Quartz, } \mathrm{SiO}_{2}$ | 2.9 |
| $\text { Calcite, } \mathrm{CaCO}_{3}$ | 9.5 |