
Let's start with the equilibrium theory of tides, and let's ignore the Sun for a moment. The moon accounts for about 2/3rd of the Ocean tides anyway, so we'll have almost everything. Also, the concepts we develop for the moon apply equally to the Sun-Earth system.
There are a few simple things to keep straight with tides. The first involves the assumptions we make for the equilibrium theory, when trying to show the simplest way to understand things. In this view, there are two ocean tidal bulges on opposite sides of Earth. One is under the moon and the other is opposite to that. The one under the moon is thought of as 'gravitational.' Newton told us that every point mass in the universe is attracted to every other mass, via gravity, with resulting force proportional to the product of the masses divided by the square of the distance between the masses. He also showed that a spherical body can be represented as a point mass at its center. Tidal forcing is proportional to the ratio of mass over distance cubed.
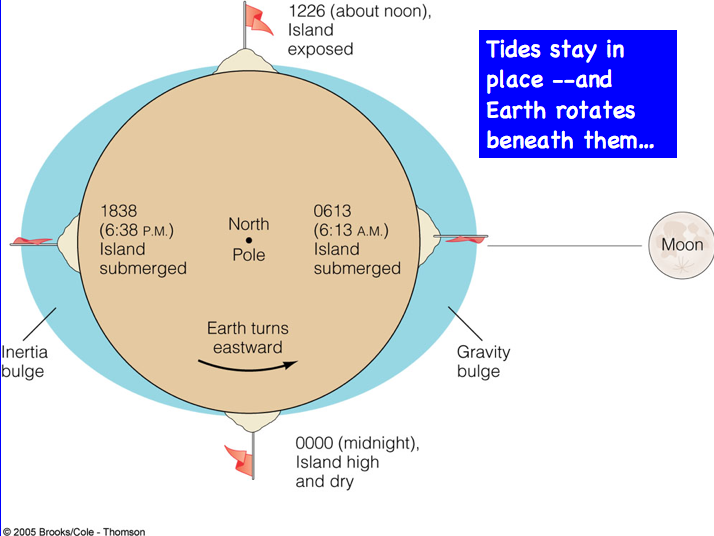
So, in our simple picture, the tidal bulge under the moon is produced by gravitational attraction between water molecules in the ocean and the moon. Now, what about the other bulge? Well, you have to think about inertia and what happens when masses rotate around a point. One relevant common experience is that of swinging a bucket of water around with your arm. The rotation produces a 'centrifugal force' that holds the water in the bucket, even when it's overhead and gravity is trying to make the water fall out of the bucket. The same thing happens during a lunar month as the Earth-moon system rotates. The moon orbits Earth, but the rotation axis for this orbit is not at Earth's center. Both the moon and Earth move during the roughly 28 day period it takes for the orbit, and because of this, water in the ocean is thrown to the outside, the same as the water in your bucket. The tidal bulge on the opposite side of Earth from the moon is produced by this inertial effect, referred to as centrifugal force.
There are some simplification here that we need to be clear about, but before we do that, let's follow through and see the logical conclusions of our model. We have two ocean tidal bulges. During a 24-hr. period, the moon is roughly stationary with respect to our simple diagram. This means that our tidal bulges are roughly stationary, and if that is true, it means that a point on Earth's surface rotates under each of these bulges and under each of the 'troughs' of low water level that are produced by the ocean water that was attracted to the moon gravitationally and thrown off the side of Earth, inertially, respectively, to produce high tides. The water to produce the high tides, associated with the tidal bulges, has to come from somewhere, and this means that sea level is lower (low tide) at locations between the high tides. Let's make things as simple as possible and imagine a situation where the moon is more or less directly over the equator, with one tidal bulge centered on the Prime Meridian. Then the other tidal bulge is centered on 180 deg. longitude. Imagine we are on the beach in Ecuador, and lets see what happens. During a 24-hour period, we'll have two high tides and two low tides, as our coast rotates under a tidal bulge (high tide) then a trough (low tide) then the other bulge (high tide) and the other trough (low tide). This situation is referred to as semi-diurnal tides and this type of tidal situation is the most common along coasts world wide. Now, let's think a bit more carefully about our assumptions and the equilibrium theory.

Tides are a product of Gravitational forces and Inertial (or Centrifugal) forces. Tides are produced by the Moon and the Sun.
Tidal forcing is proportional to:
Moon:
Sun:
The Moon has about 2x the effect of the sun.
First, let's realize that both tidal bulges in our model are produced by gravity in a rotating reference frame. The moon is in orbit around Earth due to gravitational attraction. The Earth-moon system rotates around it's center of mass, which is located at a point within Earth, but not at Earth's center. How would you go about calculating the location of the center of mass? So, when you see a diagram of Earth with two bulges, one labeled gravitational and one labeled 'centrifugal,' you can smirk and think about why it's not strictly correct; the 'centrifugal force' is actually produced by gravity and inertia. Earth is rotating around the center-of-mass in a 28 day period, and ocean water is thrown off toward the outside (think of your bucket of water.)
Ok, is that all? Well, think about the water in the Atlantic ocean and then think about a place like, say, Daytona Beach. What if the moon is actually over the longitude of Kansas? Hmmm, where are the tidal bulges? For the Atlantic, one bulge might be toward the west coast of the ocean basin, but clearly the ocean tidal bulge is not over Kansas. Here's the problem with the equilibrium theory of tides: we ignore ocean basins and coastlines, and we just think in terms of an ocean that covers the entire Earth. Obviously, this isn't correct, but it allows us to make progress, so it's a good place to start. For now, we can envisage some islands that are scattered here and there, so as to have some point of reference for sea level and for reckoning high and low tide.
The equilibrium theory sounds far fetched (no ocean basins? no coast lines, humph) but when we get to the dynamic theory of tides, I think you'll see why we started simple. We're going to have to bring in Coriolis and other complicating factors. For now, let's take a couple more steps with the equilibrium theory. As we've already seen, it does a pretty good job of predicting semi-diurnal tides, which are the most commonly observed tides. What happens when the moon is not over the equator, and what about times when the moon is closer to Earth (Perigee ~ 0.36x10^6 km) or farther from Earth (Apogee, ~ 0.4x10^6 km)? The moon's orbit around Earth is elliptical, so at certain times of the lunar month it will be closer to Earth. When the moon is closer to Earth, the 'gravitational' bulge is larger than when the moon is farther from Earth. Recall that the plane of the moon's orbit around Earth is generally not parallel to the equator and can be as much as 28.5 degrees. When the moon's declination is large, an interesting 12-hour asymmetry develops for semi-diurnal tides, and it's possible to understand it with the equilibrium theory of tides. The tidal bulges are positioned under the moon and antipodal to this point. Therefore, when a given location on Earth makes one revolution in a 24 hour period it experiences one high tide that is higher than the other and one lower low tide. Despite the success of the equilibrium theory of tides, at some point we have to admit that Earth is not covered by a single ocean.
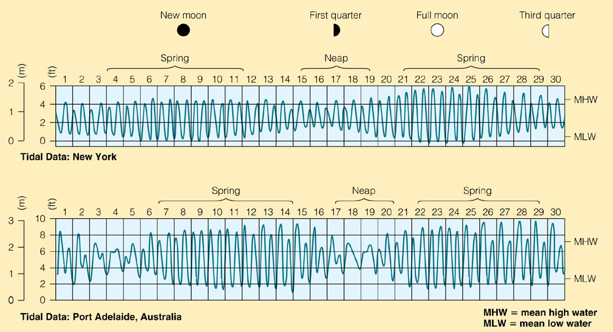
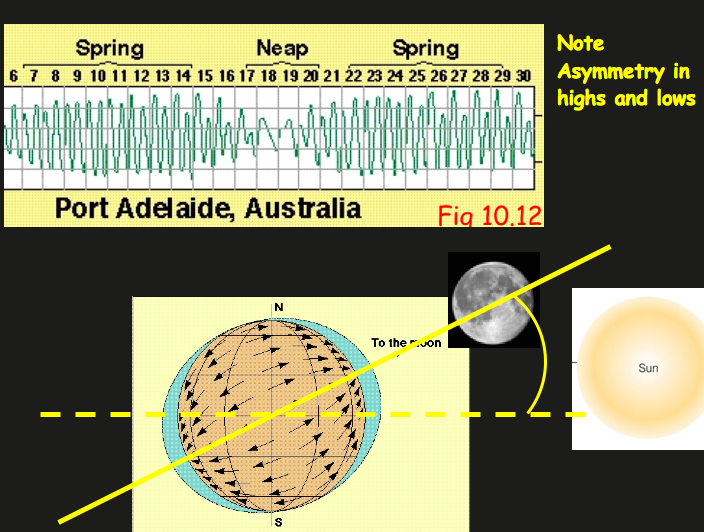
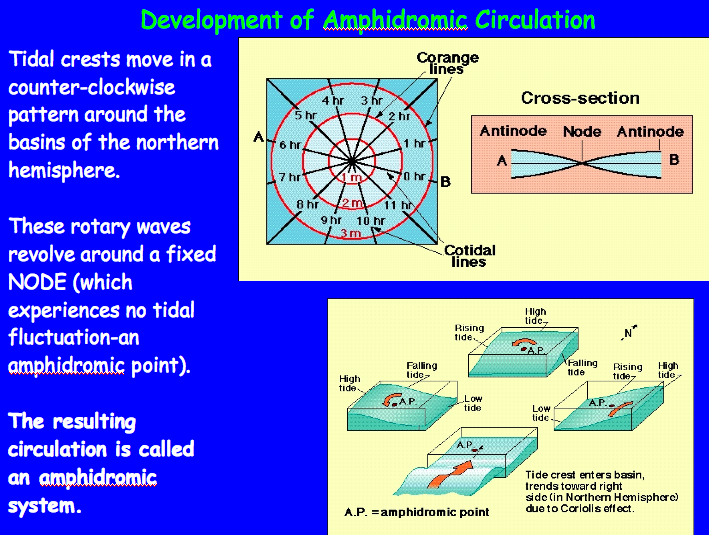
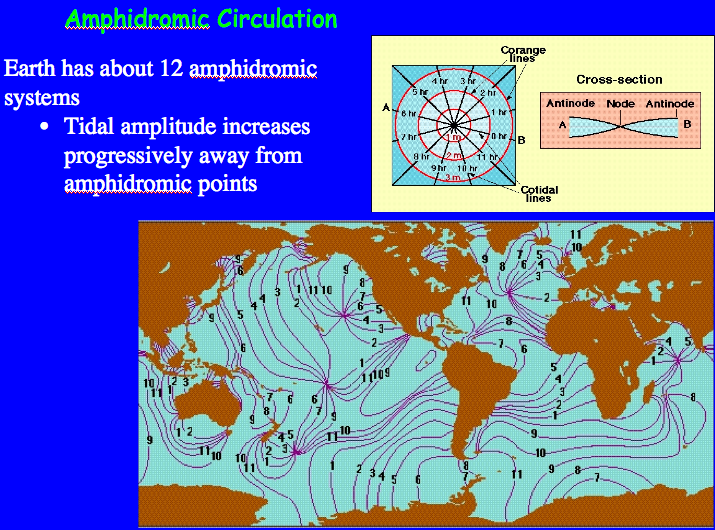
The dynamic theory of tides takes into account ocean basins of finite size and other complexities associated with coastlines. Many factors must be taken into account in order to accurately predict the tides in a given coastal setting. For example, the solid Earth experiences a tide --the amplitude of which can be 10 cm or more-- and the finite viscosity and flow properties of water need to be taken into account in order to predict resonance effects where water is flowing in and out of a restricted basin (e.g., the Bay of Fundy or the Gulf of Mexico.) The dynamic theory of tides is complex, but includes a simplifying concept know as amphidromic circulation. The idea is that tides can be thought of as shallow water waves that circulate around a point in the ocean, known as the amphidromic point. The tidal range is zero at the amphidromic point and increases with distance from this point, such that tidal range is maximum along the coast lines far from the amphidromic point (which is generally near the center of the ocean basin.) It's useful to think first in terms of a hypothetical ocean basin (we can assume it's square in map view) and then once we have the general picture down, to look at a real amphidromic circulation.
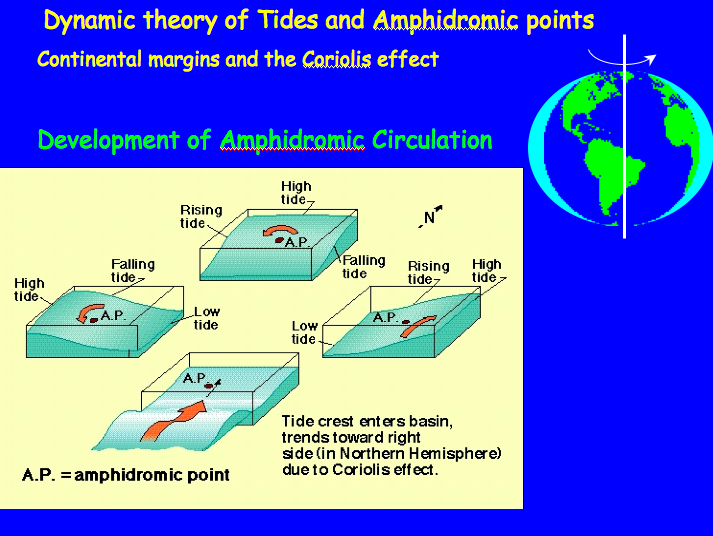
Amphidromic circulation stems from two basic effects. First, the water in a given ocean basin stays in that ocean basin. So when Earth spins under the tidal bulges, rather than the water staying in place as the Earth spins, as we assumed in the equilibrium theory, the water first builds against the west side of the ocean basin, and then sloshes back toward the center of the ocean as the continent spins under the moon, or antipodal to it. The water sloshes from West to East (think of a big basin of water that you tip from side to side --this is the scale that we are thinking in terms of for tides) but rather than going in a direct line, the motion is impacted by the Coriolis effect. In the Northern hemisphere it causes the wave to bend to the right, creating a counter-clockwise circulation, and it's the opposite in the Southern hemisphere. The tidal bulge sloshes from west to east, but ends up against the southern coast of our ocean basin. Then it sloshes back toward the center, from south to north, but it's bent to the right (Northern Hemisphere) and ends up against the East side of the ocean basin. In the Northern Hemisphere, this creates a ccw amphidromic circulation around the amphidromic point.
OK, that's it for Tides. Complete the activity on Canvas and you'll be in good shape.
Meantime, spend time on your projects and catch up with other work.
Recall: shallow water waves occur when water depth is less than roughly a factor of one half of the wavelength.
And, make plans to watch the next lunar eclipse.
A fun tool to find eclipses (lunar and solar) near you: Time and Date.
Once you've completed all lesson tasks, think about how you would teach a topic from this lesson in your own classroom; that might be a useful start for thinking about your Capstone Project for the course