Compounding
In order to compare different alternatives in an economic evaluation, they should have the same base (equivalent base). Compound interest is a method that can help applying the time value of money. For example, assume you have 100 dollars now and you put it in a bank for interest rate of 3% per year. After one year, the bank will pay you . Then, you will put the 103 dollars in the bank again for another year. One year later, you will have . If you repeat this action over and over, you will have:
Which can be written as:
In general:
The value of money after nth period of time can be calculated as:
Which F is the future value of money, P is the money that you have at the present time, and i is the compound interest rate.
Example 1-1:
Assume you put 20,000 dollars (principal) in a bank for the interest rate of 4%. How much money will the bank give you after 10 years?
So the bank will pay you 29604.8 after 10 years.
Discounting
In economic evaluations, “discounted” is equivalent to “present value” or “present worth” of money. As you know, the value of money is dependent on time; you prefer to have 100 dollars now rather than five years from now, because with 100 dollars you can buy more things now than five years from now, and the value of 100 dollars in the future is equivalent to a lower present value. That's why when you take loan from the bank, the summation of all your installments will be higher than the loan that you take. In an investment project, flow of money can occur in different time intervals. In order to evaluate the project, time value of money should be taken into consideration, and values should have the same base. Otherwise, different alternatives can’t be compared.
Assume you temporarily worked in a project, and in the end (which is present time), you are offered to be paid 2000 dollars now or 2600 dollars 3 years from now. Which payment method will you chose?
In order to decide, you need to know how much is the value of 2600 dollars now, to be able to compare that with 2000 dollars. To calculate the present value of a money occurred in the future, you need to discount that to the present time and to do so, you need discount rate. Discount rate, i, is the rate that money is discounted over the time, the rate that time adds/drops value to the money per time period. It is the interest rate that brings future values into the present when considering the time value of money. Discount rate represents the rate of return on similar investments with the same level of risk.
So, if the discount rate is i=10% per year, it means the value of money that you have now is 10% higher next year. So, if you have P dollars money now, next year you will have and if you have F dollars money next year, your money is equivalent to dollars at present time.
Going back to the example, considering the discount rate of 10%:
We can calculate the present value of $2600 occurred 3 years from now by discounting it year by year back to the present time:
Value of 2600 dollars in the 2nd years from now
Value of 2600 dollars in the 1st years from now
Value of 2600 dollars at the present time
So, it seems at the discount rate of i=10%, present value of 2600 dollars in 3 years equals 1953.42 dollars, and you are better off, if you accept the 2000 dollars now.
With the following fundamental equation, present value of a single sum of money in any time in the future can be calculated. It means a single sum of money in the future can be converted to an equivalent present single sum of money, knowing the interest rate and the time. This is called discounting.
P: Present single sum of money.
F: A future single sum of money at some designated future date.
n: The number of periods in the project evaluation life (can be year, quarter or month).
i: The discount rate (interest rate).
Example 1-2:
Assuming the discount rate of 10 %, present value of 100 dollars which will be received in 5 years from now can be calculated as:
You can see how time and discount rate can affect the value of money in the future. 62.1 dollars is the equivalent present sum that has the same value of 100 dollars in five years under the discount rate of 10%
Note:
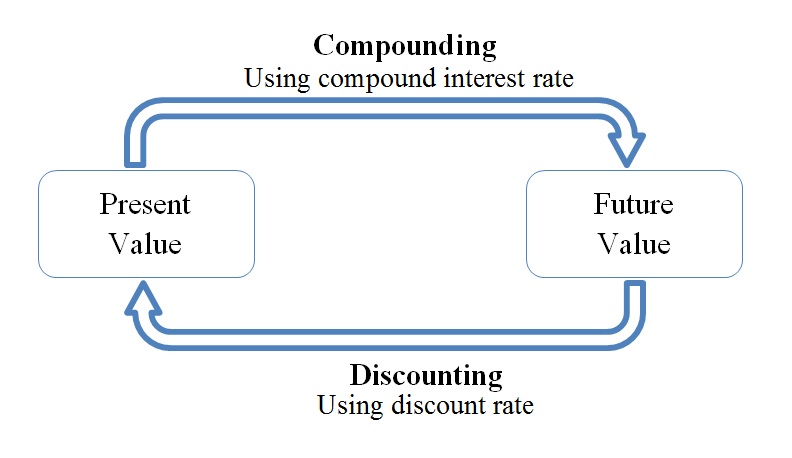
The concept of compounding and discounting are similar. Discounting brings a future sum of money to the present time using discount rate and compounding brings a present sum of money to future time.