Applications of Compound Interest Formulas

Example 2-3:

If an investment gives you 8% interest compounded annually, how long will it take to double your money, invested in present time?

F = P * F / P_{i, n}

F / P = 2 or F / P_{i, n} = 2

{(1 + i)}^{n} = 2

{(1 + 0.08)}^{n} = 2

By taking ln (natural log) or log from each side, we will have:
$\begin{array}{l} l n {(1.08)}^{n} = L n (2) \\ n * l n (1.08) = L n (2) \\ n = L n (2) / l n (1.08) = 9 years \end{array}$

It takes 9 years to double your money for an investment with 8% interest compounded annually.

The following links show how to calculate natural log using Excel:

Link 1: LN Function
Link 2: How to Return the Natural Logarithm of a Number using Formulas

Example 2-4:

Calculate the present value of following payments assuming the interest rate of 10% (compounded per period)


P=?			A₂=1000	A₃=1000	A₄=1000	A₅=1000	A₆=1000

	0	1	2	3	4	5	6

P = 1000 (P / A_{10 %, 5}) (P / F_{10 %, 1})

\begin{array}{l} Using Table 1-12: P / A_{i, n} = [{(1 + i)}^{n} - 1] / [i {(1 + i)}^{n}] \\ P = 1000 [{(1 + 0.1)}^{5} - 1] / [0.1 {(1 + 0.1)}^{5}] * 1 / (1 + 0.1) \\ P = 1000 * 3.7908 * 0.9090 = $ 3, 446.17 \end{array}

Note that here, uniform series of $1000 start from year 2. However, factor $(P / A_{10 %, 5})$ returns the P in the year before beginning of the first payment, which is year 1 here. Therefore, to calculate the present value of these uniform series of payments, we need to discount that for one year by multiplying it by $(P / F_{10 %, 1})$ .

Example 2-5:

What is the present value and equivalent series of annual end-of-period values for payments occurred in the following timeline assuming the interest rate of 10% (compounded per period)?


P=?		A₁=1000	A₂=1000	A₃=1000	A₄=2000	A₅=2000	A₆=2000	A₇=3000	A₈=3000	A₉=3000

	0	1	2	3	4	5	6	7	8	9

\begin{array}{l} P = 1000 (P / A_{10 %, 3}) + 2000 (P / A_{10 %, 3}) (P / F_{10 %, 3}) + 3000 (P / A_{10 %, 3}) (P / F_{10 %, 6}) \\ Using Table 1-12: P / A_{i, n} = [{(1 + i)}^{n} - 1] / [i {(1 + i)}^{n}] \\ P = 1000 [{(1 + 0.1)}^{3} - 1] / [0.1 {(1 + 0.1)}^{3}] + 2000 [{(1 + 0.1)}^{3} - 1] / [0.1 {(1 + 0.1)}^{3}] * 1 / {(1 + 0.1)}^{3} + 3000 \\ [{(1 + 0.1)}^{3} - 1] / [0.1 {(1 + 0.1)}^{3}] * 1 / {(1 + 0.1)}^{6} \\ P = 1000 * 2.4869 + 2000 * 2.4869 * 0.7513 + 3000 * 2.4869 * 0.5645 = $ 10434.96 \end{array}

\begin{array}{l} A = P * (A / P_{10 %, 9}) \\ Using Table 1-12 : A / P_{i, n} = [i {(1 + i)}^{n}] / [{(1 + i)}^{n} - 1] \\ A = 10435.28 * [0.1 {(1 + 0.1)}^{9}] / [{(1 + 0.1)}^{9} - 1] = 10435.28 * 0.1736 = $ 1, 811.99 \end{array}

Note that:
There are three equal series of 1000 dollars from year 1 to year 3 so the present value (at time 0) of those can be calculated as: $1000 (P / A_{10 %, 3})$ .

There are three equal series of 2000 dollars from year 4 to year 6: Because $2000 (P / A_{10 %, 3})$ gives the P of these three payments at the year 3 (one year before the first one) so we need to discount the value for three years to have the present value for time 0 so present value of three equal series of 2000 dollars from year 4 to year 6 equals:

2000 (P / A_{10 %, 3}) (P / F_{10 %, 3})

There are three equal series of 3000 dollars from year 7 to year 9: and $3000 (P / A_{10 %, 3})$ gives the P at the year 6 (one year before the first one) so we need to discount the value for six years to have the present value for time 0 so present value of three equal series of 3000 dollars from year 7 to year 9 equals:

3000 (P / A_{10 %, 3}) (P / F_{10 %, 6})

Please watch the following video, Applications of Compound Interest Formulas (Time 4:56).

Applications of Compound Interest Formulas

Click for the transcript of "Applications of Compound Interest Formulas" video.

PRESENTER: Let's work on a slightly more complicated example. We want to calculate the present value of this cash flow which are going to be annual end-of-period values for payments occurred in the following timeline considering the interest rate of 10% compounded per period. So if you notice here, we are going to have three payments of $1,000 at the end of year one, year two, and year three and three, $2,000 payments at the end of year four, five, six and three $3,000 payments at the end of year seven, eight, and nine.

As you can see here, these are not all equal. So we cannot use the factor P over A directly here. So we need some modification. First, we need to calculate the first equal series of payments, first three equal series of payments and then the second equal series of payments and the third, we calculate the third, $3,000.

For the first one, we use the factor P over A, interest rate is 10%, and we are going to have three of them. It starts from year one and finishes at the end of year three and there are three payments. Now the second three payments, the second three payments of $2,000, which are going to happen at the end of year four, five, and six.

So as you can see here, if we use the factor P over A, 10% interest rate, and three payments, this factor is going to return the present value of these three payments in one year before the first one, which is going to be here, year three. But we need it at the present time, which is year zero.

So we need to discount the result for three more years to be able to get the present value at year zero. So that's why we multiply the result of these by discounting factor by the present value for three years. So we multiply it by P over F, 10%, and three years.

Now, let's calculate the last three payments. As you can see here, the first one is at the end of the year seven. So, similarly, if we wanted to use the factor P over A, 10%, and three payments, this is going to give us the present value of these three payments at the end of year six. But we want it here at year zero.

So we need to discount this value for six more years. So that's why we multiply this with factor P over F with 10% and six periods of discounting, six years of discounting.

There's also another other way to calculate the present value of these payments. You can calculate the periods in value of each payment individually using the factor P over F and then add them all together. You might find this method to be easier and more convenient. But it needs more work and calculation.

So it's similar than what we had before. You can calculate the present value of the first payment, second payment, third payment, and so on. For the first three payments, the present value calls $1,000 multiplied by a factor P over F, 10%, and one year, because this is one year away from present time.

Second one is two years away from the present time. The third is three years away from present time. And the second three payments, you can calculate the present value with $2,000 multiplied by P over F factor, 10%, and four. And it equals four because it is happening the year four. This is four years away from present time and so on.

Credit: Farid Tayari

Note: As displayed in Figure 2-1, using Microsoft Excel, you can calculate all the present values and then add them together much more conveniently.

Figure 2-1: Calculating the total present value of all payments occurring in the future by determining each payment's present values and then adding them together using Microsoft Excel

Credit: Farid Tayari

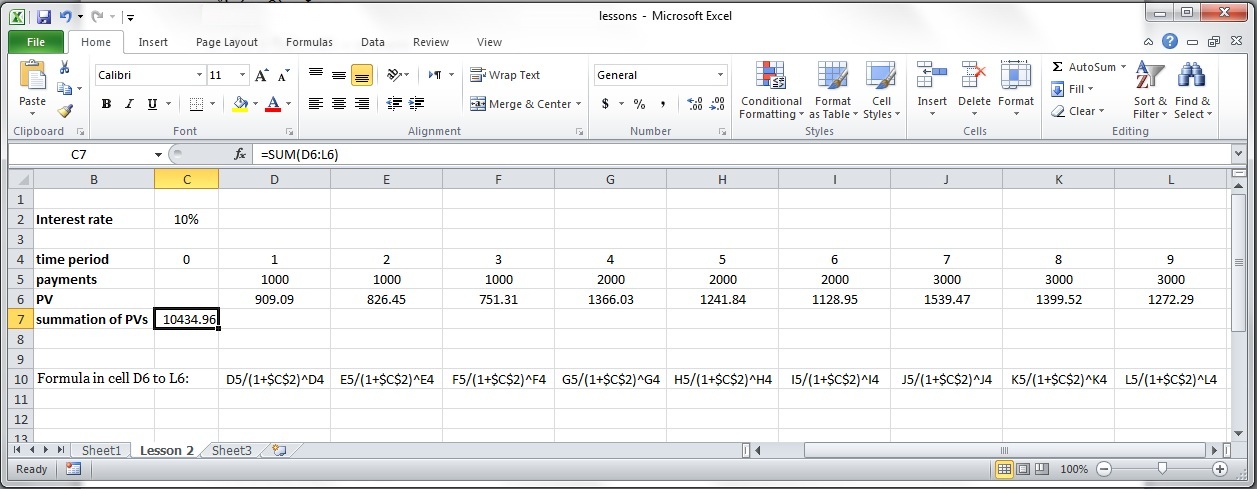
Example 2-6:

Assume you can invest in a machine that can yield the income after all expense of 1000 dollars twice in the first and second years, 2000 dollars twice in the third and fourth years, and 3000 dollars twice in the fifth and sixth years. At the end of the sixth year, the machine has a resale value of $10,000. How much can be paid for this machine at the present time with the interest rate of 10% compounded annually?


P=?		A₁=1000	A₂=1000	A₃=2000	A₄=2000	A₅=3000	A₆=3000	F=10,000

	0	1	2	3	4	5	6

\begin{array}{l} P = 1000 (P / A_{10 %, 2}) + 2000 (P / A_{10 %, 2}) (P / F_{10 %, 2}) + 3000 (P / A_{10 %, 2}) (P / F_{10 %, 4}) + 10000 (P / F_{10 %, 6}) \\ U s i n g T a b l e 1 - 12 : P / A_{i, n} = [{(1 + i)}^{n} - 1] / [i {(1 + i)}^{n}] \\ P = 1000 [{(1 + 0.1)}^{2} - 1] / [0.1 {(1 + 0.1)}^{2}] + 2000 [{(1 + 0.1)}^{2} - 1] / [0.1 {(1 + 0.1)}^{2}] * 1 / {(1 + 0.1)}^{2} + 3000 \\ [{(1 + 0.1)}^{2} - 1] / [0.1 {(1 + 0.1)}^{2}] * 1 / {(1 + 0.1)}^{4} + 10000 * 1 / {(1 + 0.1)}^{6} \\ P = 1000 * 1.7355 + 2000 * 1.7355 * 0.8265 + 3000 * 1.7355 * 0.6830 + 10000 * 0.5645 = $ 13, 805.12 \end{array}

Here we have:

Two 1000 dollars at year 1 and 2, so the present value can be calculated as $1000 (P / A_{10 %, 2})$

Two 2000 dollars at year 3 and 4, so the present value can be calculated as $2000 (P / A_{10 %, 2}) (P / F_{10 %, 2})$ . Because, similar to explanation in example 2-4 and 2-5, $2000 (P / A_{10 %, 2})$ gives the present value of these two payments at the year 2 (one year before the first one) it needs to be discounted for two years to have the present value for time 0 and present value of two 2000 dollars at year 3 to year 4 equals 2000 $2000 (P / A_{10 %, 2}) (P / F_{10 %, 2})$ .

Two 3000 dollars at year 5 and 6: similarly, PV of these two payments will be $3000 (P / A_{10 %, 2}) (P / F_{10 %, 4})$ . Because $3000 (P / A_{10 %, 2})$ returns the present value at year 4 and it is required to be discounted for 4 years to give the present value of these payments at time zero.

Figure 2-2 displays how you can calculate the present value in Microsoft Excel by adding up all the present values of payments occurring in different time periods.

Figure 2-2: Calculating the total present value of all payments occurring in the future by determining each payment's present values and then adding them together using Microsoft Excel

Credit: Farid Tayari

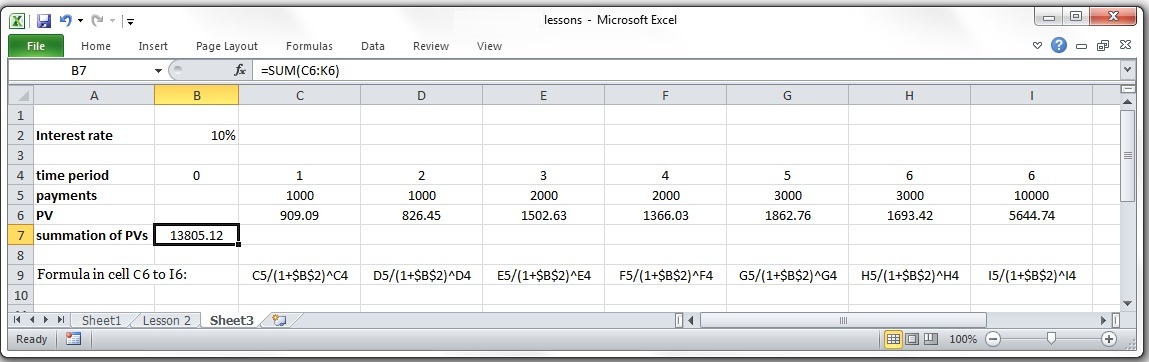
Example 2-7:

In order to pay off a 100,000 dollars mortgage in 20 years with interest rate of 8% per year (compounded annually), how much will the annual end-of-year mortgage payments be?


P=100,000		A=?	A=?	A=?		A=?

	0	1	2	3	...	20

\begin{array}{l} A = 100, 000 * (A / P_{8 %, 20}) \\ Using Table 1-12 : A / P i, n = [i {(1 + i)}^{n}] / [{(1 + i)}^{n} - 1] \\ A = 100, 000 * [0.08 {(1 + 0.08)}^{20}] / [{(1 + 0.08)}^{20} - 1] = 100, 000 * 0.101852 = 10, 185.22 dollars per year \end{array}

Example 2-3:

Example 2-4:

Example 2-5:

Example 2-6:

Example 2-7:

Navigation

EMS

Programs

Related Links