Lesson 6 - Cost-Benefit Analysis and Decision Making, Cont'd.

Lesson 6 Overview

In one sense, energy projects are no different than playing the roulette wheel in Las Vegas. Both are inherently risky, and you may well not have the shirt left on your back at the end. Actually, in one important sense, you should feel more confident about the roulette wheel than with energy projects – with roulette at least you know how terrible your odds are, and nothing is going to change those terrible odds. Because the financial fate of energy projects winds up so often in the hands of market and political factors, both of which can turn on a dime (just ask the coal industry following the publication of the Clean Power Plan [1], or electricity demand response companies like EnerNOC when a major aspect of its business model was overturned by the DC Circuit Court [2] in 2014 - even though that ruling was eventually overturned by the Supreme Court), or even the renewable energy industry during 2022 when Build Back Better was defeated, but the inflation Reduction Act passed Building A Clean Energy Economy [3], it can be difficult to know whether your project has a good or bad chance of succeeding. Given the nature of energy project investing – large up-front capital costs that must be recovered over a long duration – it’s sometimes a wonder that anything gets built at all!

The basic problem here is that the future is uncertain. In this lesson, we will look at a few different ways of considering uncertainty in project evaluation. Uncertainty has lots of different sources – markets may shift during a project cycle, making commodities more or less valuable; regulations may change; or public opposition to a project may be stronger than initially anticipated, making project permitting and siting all but impossible. Our focus here primarily will be on quantitative methods for incorporating uncertainty into project analyses, rather than on the sources of uncertainty themselves.

Learning Outcomes

By the end of this lesson, you should be able to:

Discuss topics related to cost-benefit analysis and decision making
Calculate the expected monetary value of an energy project in the face of one uncertain variable
Illustrate the concept of Value at Risk for an energy project
Explain commodity price risk and how it could affect your project
Explain what sensitivity analysis is and how you will use it in your project
Explain two types of uncertainty and how you might mitigate these risks in your project

Reading Materials

We will draw on sections from the following readings. The readings on coal-fired power plants and wind plants are a bit out of date but are useful illustrations of the types of uncertainty that energy projects face in the real world.

Registered students can access copies of the readings in the Lesson 6 module.

What is due for Lesson 6?

This lesson will take us one week to complete. Please refer to the Course Calendar in Canvas for specific due dates. Specific directions and grading rubrics for assignment submissions can be found in the Lesson 6 module in Canvas.

Participate in the Zoom call
Complete Quiz 4

Questions?

If you have any questions, please post them to our Questions? discussion forum (not email). I will not be reviewing these. I encourage you to work as a cohort in that space. If you do require assistance, please reach out to me directly after you have worked with your cohort --- I am always happy to get on a one-on-one call, or even better, with a group of you.

Hindsight is Always 20/20

Before we get into quantitative methods for considering uncertainty in energy project evaluation, have a look at the piece from the EIA on the wind production tax credit [5], as well as the following story from CNN on nuclear energy [7]. (Note that the EIA story is still relevant, even though the debate on the wind production tax credit has now come and gone.)

There are certainly enough differences between the situations being faced by the wind and nuclear industries. But the commonality among them here is that both of these low-carbon power generation technologies face substantial uncertainty that will affect project investment decisions going forward. Wind energy has enjoyed a number of years of rapid growth in the U.S. and in Europe, but it is unclear how long that level of growth can be sustained. Nuclear energy appears to be in a period of decline. Whatever happened to the “energy transition” towards low-carbon electricity generation?

Figure 6.1 shows a screenshot from the PJM Renewable Dashboard [8], which illustrates all renewable energy projects within the PJM footprint that are currently in the queue for permission to interconnect to the PJM transmission grid. (There isn’t anything particularly special about PJM here, except that they have this nice graphical display of proposed and pending renewable energy projects.) The figure, which changes frequently as new projects are added and withdrawn from the queue, suggests a lot of enthusiasm for renewable electricity generation in PJM, particularly solar and wind. In fact, until coal-fired power plants started announcing their intention to retire a couple of years back, wind energy represented the largest source of planned new generation capacity of any type in the PJM system (yes, even more than natural gas, though that is no longer true as gas power plant projects position themselves to replace retiring coal plants). While there is plenty of interest, the reality is that few of these projects will actually get built, because their revenue streams depend on a number of factors that are highly uncertain.

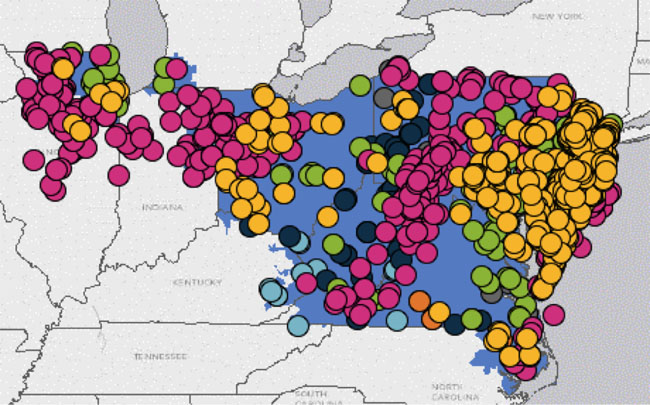
Map described in above text. Most points are between PA, OH, and VA with some in northern Illinois and Indiana.

Figure 6.1: All renewable energy projects within the PJM footprint that are currently in the queue for permission to interconnect to the PJM transmission grid

Credit: PJM Renewable Dashboard [8]. Retrieved February 17, 2024.

Virtually all investments are always made under the shroud of uncertainty, but the problem is particularly acute for energy investments. The development of energy resources typically requires large up-front capital outlays, so investors need some assurance that revenue streams over time will be sufficient for cost recovery. You can get something of a sneak peek of how changes in market institutions in the electricity industry have increased both the potential financial rewards from low-cost electricity generation but also uncertainty in power generation investment by reading the selection from Morgan, et al., “The U.S. Electric Power Sector and Climate Change Mitigation.” [9]

Returning to the nuclear and wind energy examples for a moment, these two technologies nicely represent two distinct but equally important sources of uncertainty facing energy projects.

The example with nuclear energy is primarily an illustration of market uncertainty. Just a few years ago, before the natural gas supply boom, electricity prices were high and nuclear power (having very high reliability and low production costs) was highly profitable. Companies that ran large fleets of nuclear power plants well – the biggest in the United States was Exelon – earned large returns for shareholders. Many existing nuclear power plants continue to make money, though the number of nuclear power plant retirements has accelerated in recent years. The biggest problem facing new nuclear plants, as well as some existing plants, is uncertainty in the market price of electricity. In deregulated electricity markets, the price of electricity is most often driven by the price of natural gas. As gas prices have plummeted with the unconventional natural gas boom, so have electricity prices. This squeezes profit margins for existing plants and makes the financial prospects for new plants look bleak. Will natural gas prices rise again in five to ten years (roughly the timeline for a new nuclear build in the United States)? Who knows – current markets are not betting on it, as you could observe by looking at the futures curve for natural gas.

The example with wind energy is primarily an illustration of regulatory uncertainty. As we have discovered, wind energy is not always competitive with other forms of power generation without some form of subsidy or incentive (the same could actually be said for most low-carbon power generation technologies, including nuclear). The production tax credit (PTC) was implemented in order to provide a boost to the wind industry. The PTC basically amounts to a direct payment of a bit more than $20 per MWh for all qualifying wind energy plants. Other countries have implemented subsidy programs similar to the PTC, such as feed-in tariffs. But as the EIA article points out, since the PTC does not represent a long-term commitment by the U.S. government (it needs to be renewed periodically), when the PTC is not renewed, wind energy investments shrivel because the future availability of subsidies is uncertain. The piece by Morgan, et al., points out that the lack of a commitment to a carbon policy by the United States has been a major barrier to the development of a variety of low-carbon energy resources – not just wind and solar but also low-carbon bio-energy and technologies that can capture and store greenhouse gas emissions.

Other major sources of uncertainty for the energy project include:

cost overruns (for large energy facilities in particular, cost overruns have been notoriously problematic);
performance uncertainty – plants may not work as expected, which was a problem plaguing the nuclear energy industry in the United States for many years;
permitting and siting risk – in many countries, citizens are increasingly reluctant to allow large energy facilities to be sited in their communities.

Uncertainty cannot be eliminated, but we can incorporate it into our project analyses in a few different ways, as we’ll discuss in the next several components of the lesson. Our use of the word “uncertainty” here rather than “risk” is purposeful. Use of the term “risk” implies some knowledge about the probabilities of uncertain events, like a coin flip or the roll of some dice. But placing probabilities on specific events isn’t always straightforward or even possible. So, we use the broader term “uncertainty” to describe situations where some set of future outcomes is unknown. In particular (for our context), these outcomes are unknown at the time that some decision is to be made. Broadly, we can identify a few different types of such decision situations:

decisions where all outcomes are known with certainty through net present value calculations;
decisions where some outcomes are unknown, but we are able to identify a set of possible outcomes and apply probabilities to those outcomes;
decisions where were are not able to apply probabilities to all outcomes, either because we have insufficient information to determine probabilities or we are unable to think of all possible outcomes.

We will first discuss decision problems of the second type, then move on to the third type.

Expected Monetary Value and Value at Risk

Before we dive into probability and expected monetary value (EMV), we will introduce a motivational problem from the petroleum industry. You are exploring the possibility of drilling a potential new oil field. You can either do the drilling yourself, or you can “farm out” the drilling operation to a partner. The field in which you are proposing to drill may or may not have oil – you don’t know until you drill and find out. If you drill yourself, you take on the risk if the field is not a producer, but if the field is a producer, you don’t need to share your profits with anyone. If you farm out the drilling operation, you are not exposed to any losses if the field is not a producer, but if the field is a producer, the drilling company will take the lion’s share of the profits. Table 6.1 shows the net present value of the prospective oil field.

Table 6.1: Net Present Values of the Oil Field Problem
Activity	Field is Dry	Field is a Producer
Drill Yourself	-$250,000	$500,000
Farm Out	$0	$50,000

Clearly, if you knew the field was a producer you would want to drill yourself (and if you knew it wasn’t, then you would not want to drill at all). But you don’t know this before you make your drilling decision. What should you do?

Suppose that you had enough information on the productivity of wells drilled in a similar geology to estimate that the probability of a dry hole was 65% and the probability of a producing well was 35%. Do these probabilities make your life any easier?

These decision problems can be solved by calculating a quantity known as the “expected monetary value” (EMV) – basically a probability-weighted average of net present values of different outcomes. Formally, the EMV is defined by determining probabilities of each distinct or “mutually exclusive” outcome, determining the NPV under each of the possible outcomes, and then weighting each possible value of the NPV by its probability. In mathematical terms, if Z is some alternative; Y₁, Y₂, …, Y_n represent a set of possible outcomes of some uncertain variable; X₁, X₂, …, X_n represent the NPVs associated with each of the possible outcomes; and P(Y₁), P(Y₂), …, P(Y_n) represent the probabilities of each of the outcomes, then the EMV is defined by:

E M V (Z) = P (Y_{1}) X_{1} + P (Y_{2}) X_{2} + . . . . + P (Y_{n}) X_{n}

The alternative with the highest EMV would be the option chosen. A decision-maker who chooses among alternatives in this way would be called an “expected-value decision-maker.”

Some things to remember about probabilities:

A probability is a number between zero and one. So P(Y_j) = 0.05 means that there is a 5% chance of outcome j occurring. If P(Y_j) = 0, it means that outcome j never occurs and if P(Y_j) = 1, it means that outcome j always occurs.
If a set of outcomes is mutually exclusive (meaning that multiple outcomes cannot occur) and exhaustive (meaning that the set captures all possible outcomes), then the probabilities of all outcomes in that set would be equal to one. Rolling a six-sided die with the outcomes {1,2,3,4,5,6} is an example. This set of outcomes is mutually exclusive because the face of the die cannot show two numbers at once (unless the die is crooked). The set of outcomes is exhaustive since it contains all possible outcomes of the die being rolled. In this case, P(1) + P(2) + P(3) + P(4) + P(5) + P(6) = 1. The set of outcomes {1,2,3} is an example of non-exhaustive outcomes, since the die could show a 4, 5 or 6 upon being rolled.

Now, back to our oil field problem. We’ll describe the problem again, using the language of expected monetary value. There are two alternatives – to drill yourself or to farm-out. The uncertainty is in the outcome of the drilling process. The set of mutually exclusive and exhaustive outcomes is {dry hole, producer}. These are the only two possible outcomes, regardless of whether you choose to drill yourself or farm-out. The NPVs of each alternative, under each possible outcome, are shown in Table 10.1. To decide whether to drill or farm out, you would calculate the EMV of each option as follows:

$\begin{array}{l} E M V (Drill) = P (dry hole) \times - $ 250, 000 + P (producer) \times $ 500, 000 \\ = 0.65 \times - $ 250, 000 + 0.35 \times $ 500, 000 = $ 12, 500 . \\ E M V (Farmout) = P (dry hole) \times - $ 0 + P (producer) \times $ 50, 000 \\ = 0.65 \times - $ 0 + 0.35 \times $ 50, 000 = $ 17, 500 . \end{array}$

In this case, you should choose to farm out the drilling operation.

The basic idea behind EMV is fairly straightforward, assuming that you can actually determine the relevant probabilities with some precision. But the meaning of the EMV is a little bit subtle and requires some degree of care in interpretation. Let’s take a very basic situation – a coin flip. Suppose that we were to flip a coin. If it shows heads, you must pay me $1. If it shows tails, then I must pay you $1. The EMV of this game, assuming that heads and tails have equal probabilities, is $0. (See if you can figure out why, based on the EMV equation and the fact that P(heads) = 0.5 and P(tails) = 0.5.) But if you think about this for a minute, how useful is the EMV? If you play the coin-flipping game once, you will never ever have an outcome where the payoff to you is $0. The payoff will either be that you gain or lose one dollar.

If you look at the EMVs from the oil-field problem, you will see the same thing. The EMV of drilling is $12,500 but there is no turn of events under which you would wind up earning $12,500 – if you drill, it would either be that you lose $250,000 or gain $500,000. Similarly, if you farm out you will never earn exactly $17,500. You will either lose nothing (payoff of $0) or you will gain $50,000. So what does the EMV mean when it tells you that farming-out is the better option?

It’s important to remember that the EMV is a type of average. If you were to play the coin-flip game or the oil-field game a large number of times under identical circumstances, and make the same decision each time (i.e., to drill or to farm out), then over the long run you would expect to wind up with $12,500 if you choose to drill and $17,500 if you choose to farm out. While the EMV may be useful for gamblers or serial investors, using EMV needs to be done with some care for stand-alone projects in the face of uncertainty.

One potential alternative to calculating EMV when probabilities are known (or can be estimated) is to use those probabilities to describe the likelihoods of gaining or losing certain amounts of money. This is the idea behind the “value at risk” for an investment project or a portfolio of projects. The value at risk (VaR) describes the amount of money that will be gained or lost with some probability, typically worst-case situations (like describing the amount of money that would be gained or lost with a 5% probability). From a decision perspective, you might want to avoid investment opportunities with a large VaR (given some probability). Many times, VaR will have a duration associated with it, most often when calculated in reference to portfolios of financial assets (like stocks or bonds).

Wikipedia has a very descriptive entry for VaR [10]. The introductory section of the Damadoran VaR paper [6] is written in clearer English, but gets into the details quickly after the first few pages.

To force the example a little bit, here is how VaR might be applied in our simple oil field problem. The field will either yield a producer (probability 35%) or a dry hole (probability 65%). Those are the only two outcomes and probabilities for this problem. If we think about the negative outcome – the dry hole – and ask how much of the value of the project might be at risk if the hole turns out to be dry, then we can calculate VaR just by using the NPVs from Table 10.1. (In this example, there is no time dimension to VaR since the project is a one-shot deal.)

If we choose the option to drill ourselves, the 65% VaR would be -$250,000. If we choose to farm-out the drilling operation, the 65% VaR would be $0. We might choose to farm out simply because the VaR technique tells us that our extreme losses would be lower if we farm-out than if we drill the well ourselves.

Decision Analysis Without Probabilities

Sensitivity, Threshold and Scenario Analysis

In the oil-field example from the previous section, the probabilities of a dry hole and a producer were known with confidence. This isn’t always true in the real world. Moreover, sometimes in real-world situations, there are so many possible outcomes that is impossible to assign a specific probability to each outcome. Suppose, just hypothetically, that oil prices could vary between $50 and $100 per barrel over the next five years. What is the probability that oil prices will average $50.03 per barrel? $50.04 per barrel? $99.30 per barrel?

In cases where determining probabilities explicitly is not possible or practical, threshold analysis and sensitivity analysis can be useful in understanding how the net present value of different alternatives may vary with some variation in key variables. Both of these techniques are useful in identifying situations under which one alternative is better than another. This can make even complex decision problems much more tractable for the decision-maker, since it reduces the problem from needing to calculate net present values for a large number of alternative outcomes to a judgment of whether one or another set of outcomes is more likely.

As we go through these techniques, we will often refer to something called a “parameter” in the decision problem. In this case, a parameter refers to a variable whose value affects the outcome of one or more alternatives – so a parameter is different from an alternative. In the oil field problem, the major parameter would be whether the field is a dry hole or whether it is a producer (so the parameter itself would be the probability of a producer versus a dry hole). The price of oil or the quantity of oil (if any) might be other important parameters for a problem such as this one.

Sensitivity Analysis

Sensitivity analysis proceeds by selecting one parameter, changing its values, and observing how these new values change the net present value (or EMV) of some alternative. If sensitivity analysis is conducted using a small range of alternative values, or if the alternative values represent different scenarios, then it is sometimes (aptly) called “scenario analysis.” There's more material on scenario analysis further down this page.

We’ll illustrate this using the oil-field problem, performing a sensitivity analysis on the EMV of the drilling option as we vary the dry-hole probability. In this case the outcome is the EMV and the parameter that we are varying is the probability of a dry hole. This analysis is pretty straightforward since we can write an expression for the EMV of drilling. We will need to use the fact that P(producer) = 1 – P(dry hole). (What rules of probability tell us that this is true?)

E M V (Drill) = P (dry hole) \times - $ 250, 000 + (1 - P (dry hole)) \times $ 500, 000

We can rearrange terms in the equation to get:

$E M V (Drill) = $ 500, 000 - $ 750, 000 \times P (dry hole)$

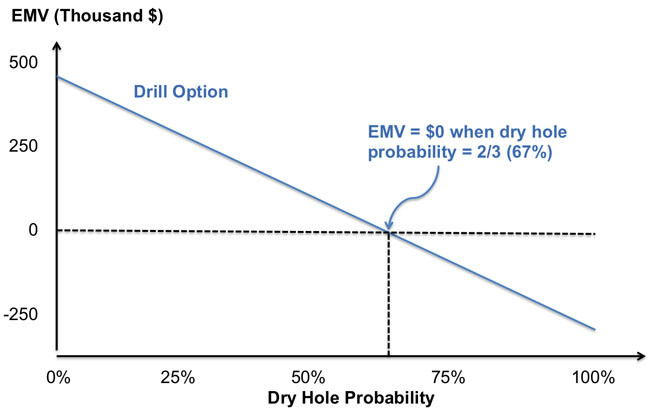
This equation tells us a couple of things. First, the EMV of drilling is going to decline as the probability of a dry hole increases. This makes sense, since we lose money if we drill ourselves and the field is not a producer. Second, the relationship between EMV and the dry hole probability is linear, so the EMV falls at a constant rate as the dry hole probability increases. We can also use the equation to find the dry hole probability where the EMV is equal to zero. We do this by setting EMV(drill) equal to zero and manipulating the equation as follows:

$0 = $ 500, 000 - $ 750, 000 \times P (dry hole)$

$P (dry hole) = $ 500, 000 / $ 750, 000 = \frac{2}{3} (67 %)$

Normally, sensitivity analysis is utilized to visualize the change in net present value or EMV with the change in some parameter of interest. For the drilling option, this is shown in Figure 10.2, which plots the EMV versus the dry hole probability. Also shown in Figure 6.2 is the dry-hole probability where the EMV is equal to zero.

See image caption. X axis = dry hole probability. Y axis ranges from -250 to 500.

Figure 6.2 - A Dry Hole Probability Graph (EMV=0). Shows the EMV decreasing with increasing dry hole probability, labeled "Drill Option." Drill Option EMV - $0 when dry hole probability = 2/3 (67%).

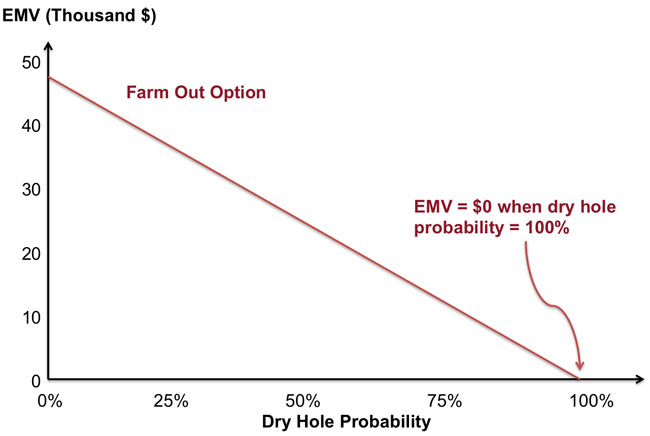
As an exercise for yourself, perform the same sensitivity analysis on the option to farm-out. The parameter is still the same (the probability of a dry hole) but the outcome is different (the option to farm-out versus the option to drill). Your graph should look like the one in Figure 6.3.

Figure 6.3 - A Dry Hole Probability Graph (Farm Out Option). Depicts the relationship between Dry Hole Probability (x axis) and EMV (y axis). Line shows EMV decreasing from 50 thousand dollars to 0 as Dry Hold Probability increases from 0% to 100%.

Threshold Analysis

Threshold analysis (also called break-point analysis) seeks to identify the value of a parameter where the best decision changes. Instead of asking what the probability of a producer versus a dry hole might be (and what are the associated EMVs of the option to drill or farm-out), a threshold analysis would ask how likely would it need to be for the field to be a producer for the expected-value decision-maker to choose the option to drill.

Threshold analyses can proceed graphically or algebraically. We will use the oil field example to illustrate both. Remember that the EMV of both the drilling and the farm-out options are functions of the dry-hole probability and of the NPVs for drilling and farming-out. Holding the NPVs constant as in Table 10.1, we can write a mathematical expression for the EMV of each option as a function of the dry-hole probability P(dry hole). We will need to use the fact that P(producer) = 1 – P(dry hole). (What rules of probability tell us that this is true?)

$E M V (drill) = P (dry hole) \times - $ 250, 000 + (1 - P (dry hole)) \times $ 500, 000$

$E M V (farm out) = P (dry hole) \times - $ 0 + (1 - P (dry hole)) \times $ 50, 000$

If we graph the EMVs together on the same set of axes (as in Figures 6.2 and 6.3), the point at which the two lines cross would be the threshold. Figure 6.4 illustrates this crossing point. Note that the scale of the axes, especially the horizontal axis, is different than in Figures 6.2 or 6.3.

Figure 6.4 - Dry Hole Probability (Crossing Point). Shows EMV versus Dry Hole Probability with Drill and Farmout options. The x-axis represents the Dry Hoole Probability ranging from 50% to 70%, while the y-axis shows EMV from -75 to $150,000.

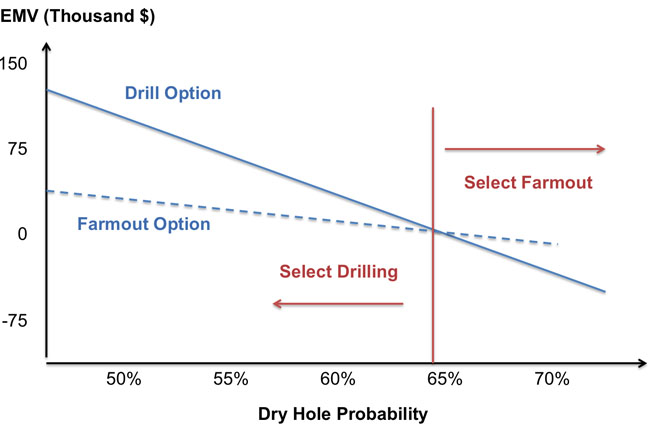
Looking carefully at Figure 6.4, we can see that at a dry hole probability of around 65% or lower, the EMV of drilling is higher than the EMV of the farm-out option (this is why the drilling curve is above the farm-out curve). If the dry hole probability is above 65%, then the farm-out option has a higher EMV.

Algebraically, we can solve explicitly for the threshold value of the dry hole probability, by setting EMV(drill) equal to EMV(farm-out) and solving for the dry hole probability that makes these EMVs identical. Here we go!

$\begin{array}{l} E M V (drill) = E M V (farmout) \\ $ 500, 000 - $ 750, 000 \times P (dry hole) = $ 50, 000 - $ 50, 000 \times P (dry hole) \\ $ 450, 000 = $ 700, 000 \times P (dry hole) \\ P (dry hole) = 0.64 (64 %) \end{array}$

Threshold analysis in particular can be a very powerful way of making difficult decisions seem more tractable. Even in the simple oil-field problem, the relevant question for the investor evaluating the oil-field decision is not to determine the exact probability of the field being a producer. The threshold analysis approach asks the potential investor whether they believe that there is more than a 65% chance of the field being dry. If so, then they should farm out drilling or not drill at all. If not, then the investor should choose to drill themselves.

Scenario Analysis

Scenarios about future outcomes or states of the world can be powerful tools for getting decision-makers to think about uncertainty. While scenario analysis is simpler than a sensitivity or a threshold analysis, scenarios can often be made up of specific values of multiple parameters. Scenario analysis is not about predicting the future or making projections. Like sensitivity and threshold analysis, it is a way to get decision-makers to consider different possible future states of the world, to identify the drivers that might lead to those states of the world, and to make plans for those possible states of the world.

In the energy world, one of the pioneers of scenario-based planning has been Shell [12], which started using scenario-based planning in the 1960s, as computer-aided decision-making was emerging among large businesses. Shell adopted scenario planning when it (and other large energy companies) were surprised by the emergence of environmentalism and the OPEC cartel as unforeseen but potentially disruptive forces to their business. The Harvard Business Review [13] has a nice article about Shell's development and use of scenario planning. (The article is also available through Canvas.)

The process of scenario planning has a number of steps:

Determine drivers of change (largely done via brainstorming)
Determine links and interdependencies among drivers of change - an example is that technological and regulatory change may be intertwined. The purpose of this step is to recognize the existence of interdependent or connected drivers of change, and possible directions of influence.
Group drivers that are logically connected into "scenarios." Typically, at this stage the scenarios are brainstormed, without too much worry about whether the scenarios overlap with or contradict one another.
The larger set of scenarios is reduced to a smaller set of scenarios. In Shell's method, the aim is to get to around three scenarios - the idea is that this avoids a focus on one scenario as being the most or least likely. It's also important to recognize at this stage that scenarios are different than alternatives so we don't really talk about scenarios that might be preferred over others. At this stage, scenarios are ideally complementary rather than in opposition (having a good and bad scenario, for example).
Tell a story about each scenario. This often involves giving each scenario a name and including some context - not just the specific parameter values associated with different scenarios but the events that might lead to those scenarios.

Scenario planning has its critics - one thing about scenarios, for example, is that good scenarios are based around plausibility and not probability. This can lead to different decision-makers having different views of likely versus unlikely states of the world. Regardless, scenario planning is still a widely-used tool for decision-making.

Lesson 6 Summary and Final Tasks

Uncertainty is a critical problem in the evaluation of energy projects, owing to the capital-intensive nature of most projects and the need for cost recovery over long time frames. Projecting the market and regulatory conditions over such long time frames is often fraught with error and, in hindsight, bad decisions. Two of the major sources of uncertainty facing energy projects are market uncertainty (market prices or price volatility are not known with certainty into the future) and regulatory uncertainty (relevant policy measures cannot be anticipated with perfect foresight). Since low-carbon energy projects in particular need policy support to achieve widespread market deployment, regulatory uncertainty in the form of a lack of climate-change policy or inconsistent application of subsidies and incentives can be especially difficult for investors in low-carbon energy technologies. Even if the future cannot be predicted perfectly, there are ways to incorporate uncertainty into project evaluation. Calculation of expected monetary values (EMV) is possible when all possible outcomes can be identified and probabilities assigned, but since the EMV represents the average payoff over a large number of trials, it may not be appropriate for single energy project evaluation. Sensitivity analysis and threshold analysis are ways of visualizing how the NPV or EMV of a project may change under different values of key parameters.

Reminder - Complete all of the Lesson 6 tasks!

You have reached the end of Lesson 6! Double check the What is Due for Lesson 6? list on the first page of this lesson to make sure you have completed all of the activities listed there before you begin Lesson 7.