Recall from EME 810 that the time that we use in solar energy engineering is the apparent time and path of the sun relative to the aperture or collection device, called Solar Time. Because the Earth is a rotating sphere (360deg) that completes a rotation every 24 hours, 360 divided by 24 gives 15 degrees of rotation per hour, or one degree every 4 minutes. The chronological time that clocks use do not account for your geographic location beyond correcting for a time zone. Within a time zone, if you are geographically close to the next time zone, a larger time correction is necessary to convert to solar time. Additionally, the Earth does not rotate perfectly, rather, it wobbles on its axis creating what is known as an analemma. As such, an "equation of time" is necessary to convert between solar and standard time, as given in D&B equations 1.5.2 and 1.5.3.
Correcting with the Equation of Time: Accounting for Wobbles
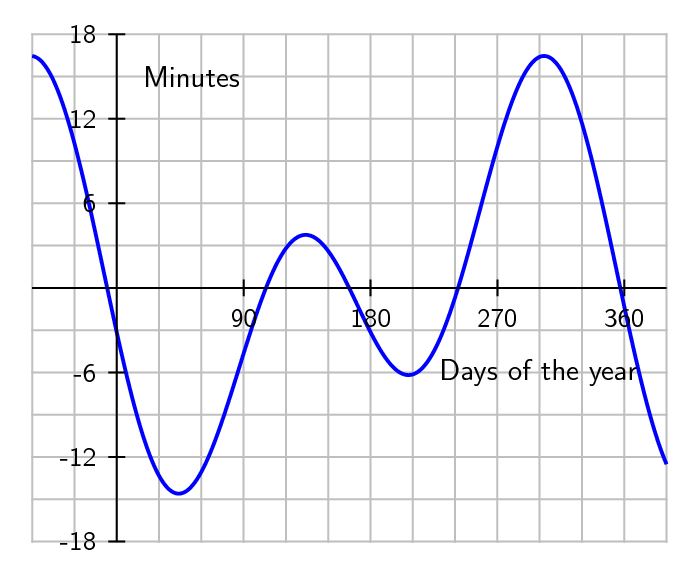
Even in Greenwich, where no longitudinal correction is necessary, "noon" UTC will generally not be the time when the sun is directly overhead. We can see in the plot below that watch time and solar time are the same in Greenwich for only 4 days in the year.
- There are deviations of up to $\pm16$ minutes (regardless of your location on the planet).
As you will have read, our interpretation of watch time assumes an even progression for Earth's planetary rotation, with no weebles or wobbles or precession of the polar axis. However, you will now know that wobbling occurs, and there is great variability in the rotation of the Earth throughout the months of the year. This is why we add leap years and leap seconds to our calendars. So we create a "mean time" based on the length of an average day to keep things simple. Solar time has to correct for this mean time approximation.
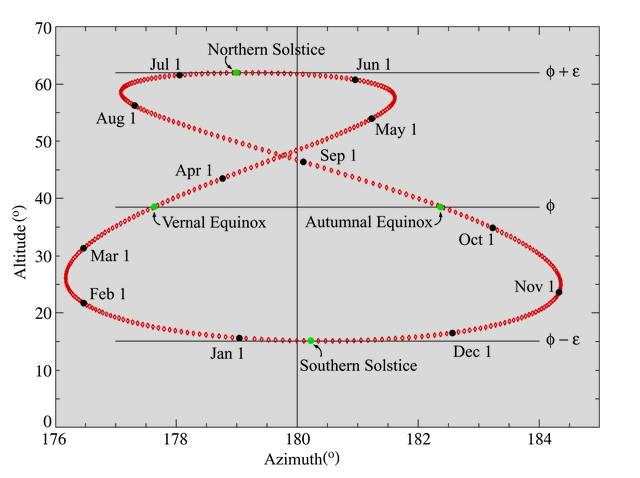
For views of amazing solar analemma photography by Anthony Ayiomamitis, please visit his solar image gallery. The gallery has a series of composite of images, taken at the same watch time every few days for an entire year to record the position of the sun. We call the shape an analemma. An analemma is a beautiful way to capture both the range of declination $\delta$ (along the length of the analemma) and the Equation of Time Et (the expansion or width of the analemma) in a graphical format. Notice how there is a big loop and a little loop, and compare the same big waves and little waves in the first image of the Equation of Time correction above. If you were to draw a line down the center, you would have removed the error from watch time, and you would be one step closer to solar time.
Correcting for Little Longitude Changes: Inside Time Zones
Recall from EME 810 that there is a correction for longitude based on where you are within your timezone. Where you live, or where your future solar site assessment will occur, will likely be well within the edge of a time zone (meaning $\lambda_{std} - \lambda_{loc} \neq 0^\circ$). We already learned that every $1^\circ$ of angular rotation on Earth is equal to 4 minutes of time. Standing in one spot on the surface, this means 4 minutes of relative time correction locally per degree of deviation from a Standard Meridian ($\lambda_{std}$). So locales will have a local longitudinal refinement to account for, in order to account for not living directly on a 15 degree incremental Standard Meridian on Earth.
Standard Meridians define the beginning of a time zone, and not the end of a time zone. So you are always going to look to the start of a time zone to find the Standard Meridian.
There are a few other cities that actually are well seated for solar time zone correction (close enough for our calculations):
- Philadelphia is fairly close to the EST standard meridian of $-75^\circ$.
- Denver is fairly close to the MST standard meridian of $-105^\circ$.
My client lives someplace other than a Standard Meridian, how do I account for that?
First, go to Google and type "<insert city name> longitude". You should get a quick response of both the Longitude ($lambda$) and the latitude (our symbol for latitude is lowercase Greek "phi": $phi$), represented in decimal form (more useful to us for trigonometry and angles). Do this now for your current location, and note (self check) how many degrees away you are from your standard meridian (multiple of $15^\circ$).
Have you noticed that real time zones are more often political boundaries that zigzag around, rather than following an actual Standard Meridian? So, actually, there can be locales for clients that are East of their own time zone Standard Meridian, instead of the normal relative locations West of the time zone Standard Meridian. This is why, in the reading, you will see $\pm4$ minutes per degree of local longitudinal shift away from the time zone's Standard Meridian.
Self Check
Work through Example 1.5.1 (page 11) in the D&B text by hand with a paper and pen(cil).
