We assume that the system is at steady state and at a state of equilibrium. Adopting these two assumptions is essential to the developing of the equations that we use to solve these problems. These assumptions are convenient for modeling and have proven useful in representing the real phenomena. In conclusion, we claim that the systems maintain a state that resembles equilibrium and does not depart from it greatly. And what does steady state means? Simply stated, we say that a system is at steady state when whatever comes into the system goes out. This is, no accumulation takes place within the system.
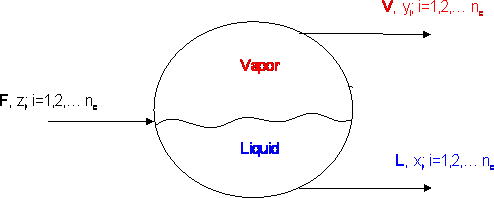
Let us consider the equilibrium cell shown in Figure 12.1. “F” moles of a feed enter our equilibrium cell with a composition “zi” and “nc” is the number of components that we have in the mixture. A flash vaporization takes place at a given pressure and temperature, and two streams come out: “V” moles of a vapor of composition “yi” and “L” moles of a liquid of composition “xi”. In steady state, a simple overall balance yields:
(12.1a)
Now we define the fractions of gas and liquid to be, respectively:
(12.1b)
(12.1c)
Therefore, if we divide equation (12.1a) by “F”, we get:
(12.2)
The same steady state assumption applies for the mass of each component separately. Here we revisit a concept we used in Module 5, when we studied the lever rule. At that point, we said that the number of moles of a component “i” per mole of mixture in the liquid phase is given by the product “xiaL”, while the number of moles of “i” per mole of mixture in the gas is given by “yiaG”. Since there are “zi” moles of component “i” per mole of mixture coming into the system, the conservation of each component in the system imposes:
(12.3)
Equation (12.3) is true for each of the components in the system. Equation (12.2) can be introduced into equation (12.3) to yield:
(12.4)
One of the concepts that we normally use in vapor-liquid equilibria is that of the equilibrium ratio, Ki. In fact, most of the computations of phase behavior of natural gas mixtures are carried out through the concept of the equilibrium ratio. By definition, the equilibrium ratio of a component “i” in a vapor-liquid mixture is defined as the ratio of the molar composition of that component in the vapor phase to that in the liquid phase,
(12.5)
In earlier literature, this concept was referred to as the equilibrium constant. In actuality, Ki is not constant but a function of the pressure, temperature, and composition of the system. However, equilibrium ratios can be fairly independent of composition when the pressure and temperature conditions are far from critical.
Therefore, today we refer to it as the vapor-liquid equilibrium ratio, Ki. We can introduce this concept into the balance in (12.4), as shown:
(12.6)
Now, solving for yi,
(12.7)
A constraint that mole fractions must satisfy is that they must add up to unity. Since we solved for yi, we can impose that the summation of all molar vapor fractions must be equal to one, i.e.,
(12.8)
If we now substitute (12.7) into (12.8), we get:
(12.9)
This equation is important for us; we call it an objective function because we can use it as the starting point for solving the vapor-liquid equilibrium problems we have posed.
However, as you may be thinking right now, this is not the only choice that we have for an objective function. In fact, we may obtain another objective function if we repeat the previous steps, while solving instead for xi. In this case, we may introduce the concept of equilibrium ratio in (12.5) into (12.6) as follows:
(12.10)
We now solve for xi,
(12.11)
If we apply the constraint that all mole fractions must add up to one,
(12.12)
Both (12.9) and (12.12) are plausible objective functions. Either of them allows us to solve the flash problem that we are dealing with. The variables that make up both equations are:
nc = Number of components,
zi = Overall composition, or composition of the feed,
Ki = Equilibrium ratios of each of the components of the mixture,
ag = Vapor fraction in the system.
What is it that we are looking for? Go back and look at the types of VLE problems that we would like to solve, as we presented them in the previous section. If we are interested in solving the flash problem, we want to know how much liquid and gas we will have inside the flash equilibrium cell. This is, given a liquid-vapor mixture of composition zi, and nc number of components, what percent of the total number of moles is liquid, and what percent is vapor? How do we split it? In this case, we would like to come up with a value for αl and αg respectively.
Equations (12.9) and (12.12) tell us that if we are able to come up with the proper values for the equilibrium ratios, Ki, which are functions of the pressure, temperature, and composition of the system, the only unknown left to solve for would be αg — exactly what we want!
Well, do not rush. We would have to come up with a way of calculating Ki’s first, and this may not be a trivial task. For the time being, let us say we “know” Ki’s. Two questions remain unanswered:
- First, is it “better” to solve the problem using equation (12.9) or (12.12)? (Recall, either of them would lead us to the answer!).
- Second, how do we solve for αg? For a complex mixture of many components, “αg” cannot be calculated explicitly.
We will address both of these questions in the next module. As for now, let us give you a hint: we will not use either equation (12.9) or (12.12) to solve the flash problem!