In the previous section, we talked of production functions and input factors. When a firm converts factors of production into products (or output), it has to incur costs for those inputs before it can sell the output in the market. In this section, we will examine some of these costs, and how they fit into the concept of a supply curve.
There are several different types of costs that a firm incurs, broken down as follows:
Fixed Costs
This is the amount of money a firm has to spend to produce something that is not related to the amount produced. It is sometimes called the Sunk Cost or Overhead. Remember: in the short run, capital is fixed, so it is capital that forms the fixed cost part of any production process. Put another way, this is money you have to spend before you produce anything. For a pizzeria, it is the cost of the building, the ovens, the meat slicer, and so on. In the oil and gas industry, it is the wells, pipelines, and refineries that have to be built to extract, transport, and transform the crude oil or gas into saleable products. In the electricity industry, it is the power plants and transmission lines.
Variable Costs
These are costs that change with respect to the quantity produced. This basically describes the non-capital factors of production: material, labor and energy. All of these things change with respect to the amount of output a firm creates. An electricity generator has to burn more coal or gas to make more electricity. A pizzeria has to consume more flour, cheese and tomatoes to sell more pizza. A consulting company needs more staff if it is to take on more projects. These factors are all variable costs in the sense that they vary with output. Sometimes, certain types of labor might be seen as "overhead," and thus, basically, a fixed cost, because this labor does not vary with output, but this is a minor detail we need not worry about at this point.
Total Cost
Total Cost = Fixed Cost + Variable Cost
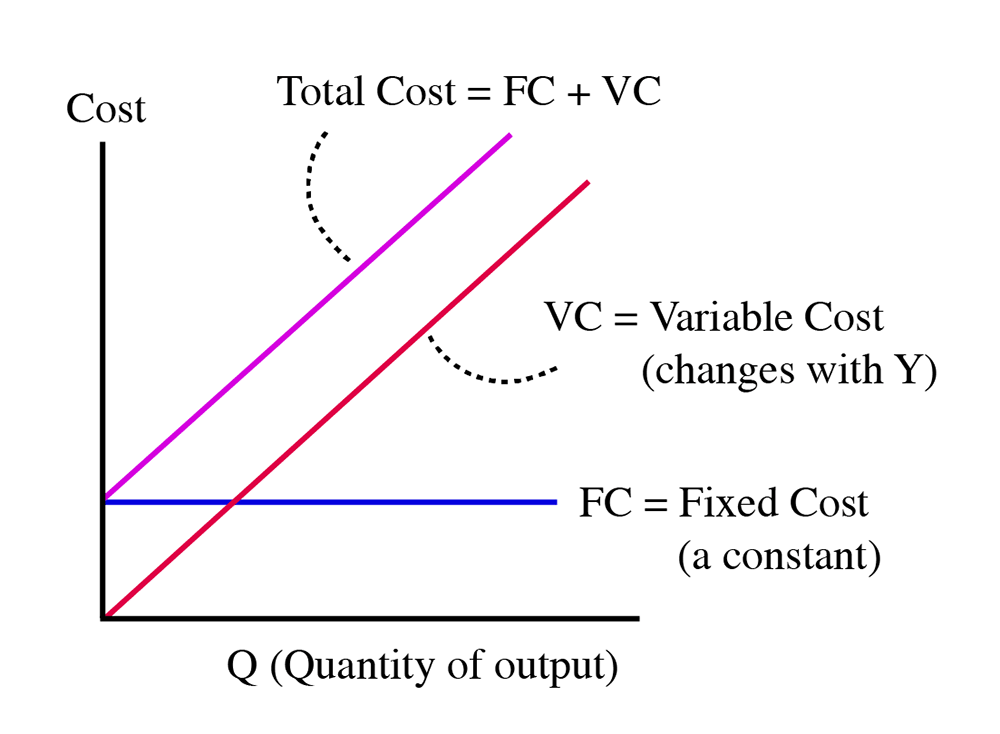
Using abbreviations, we say that .
Average Cost
An average cost is the total cost divided by the quantity:
- . (Can also be labeled as ATC: average total cost)
We can also have average fixed cost and average variable cost:
Marginal Cost
Marginal Cost is the most important cost of all. Greg Mankiw, whom we mentioned in the first lesson, calls this the “most important concept in economics.” The marginal cost is the cost of producing one more unit (or can be thought of as the cost of producing the last item). So, it is the change in total cost for some change in quantity:
where TC1 is the total cost of producing Q1 units, TC2 is the total cost of producing Q2 units of output.
We can have the Q1 = Q and Q2 = Q +1 in that case, the Marginal Cost equation will be simplified as:
Example: Assume that the fixed cost for a shoe firm is 500, and it costs 100 to produce each individual pair of shoes. For Q=1 to 10, determine the fixed cost, variable cost, total cost, average variable cost, average fixed cost, and marginal cost.
| Q | FC | VC | TC | ATC | AFC | AVC | MC |
|---|---|---|---|---|---|---|---|
| 1 | 500 | 100 | 600 | 600.00 | 500.00 | 100 | 100 |
| 2 | 500 | 200 | 700 | 350.00 | 250.00 | 100 | 100 |
| 3 | 500 | 300 | 800 | 266.67 | 166.77 | 100 | 100 |
| 4 | 500 | 400 | 900 | 225.00 | 125.00 | 100 | 100 |
| 5 | 500 | 500 | 1000 | 200.00 | 100.00 | 100 | 100 |
| 6 | 500 | 600 | 1100 | 183.33 | 83.33 | 100 | 100 |
| 7 | 500 | 700 | 1200 | 171.43 | 71.43 | 100 | 100 |
| 8 | 500 | 800 | 1300 | 162.50 | 62.50 | 100 | 100 |
| 9 | 500 | 900 | 1400 | 155.56 | 55.56 | 100 | 100 |
| 10 | 500 | 1000 | 1500 | 150.00 | 50.00 | 100 | 100 |
Practice Exercise
Assume the fixed costs for a pizza restaurant is 150 and it costs 15 to produce each pizza. For Q=1 to 10, determine the fixed cost, variable cost, total cost, average variable cost, average fixed cost, and marginal cost.
Example
When we mathematically represent a cost function, it might look something like this:
So, you will know that the Fixed Cost is the constant term (the term that does not include any mention of Q), and the Variable cost is the sum of all of the terms that include Q in some way. If a term does not include Q, then, clearly, it does not change when Q changes:
An average cost is the total cost divided by the quantity:
We can also have average fixed cost and average variable cost:
We can use the following equation to calculate the Marginal Cost, for example
Then, the total cost of producing 10 units will be given as:
Using the same function, the total cost of producing 11 units (one more unit) will be:
So, the marginal cost of the 11th unit =
Note: .
So, by canceling out the FC term, we get , and we can say that:
Of course, anything defined in discrete difference (“delta”) terms can also be described in continuous terms by using a derivative:
Practice Exercise
Following the previous example, for Q=1 to 15, determine the fixed cost, variable cost, total cost, average total cost, and marginal cost. Then try to draw the graph including the cost metrics.
Take Aways
After working through the material on this page and reading the associated textbook content, you should be able to confidently:
- define and calculate the following terms:
- fixed cost, average fixed cost
- variable cost, average variable cost
- total cost, average total cost
- marginal cost
- derive the fixed cost, variable cost, average costs and marginal cost when given a total cost function.
